基于时滞分割技术的时滞神经网络系统时滞相依全局稳定性分析

2019-06-18孙校书杨树杰

海军航空大学学报 2019年2期

毛凯，孙校书，杨树杰，刘丹

（海军航空大学，山东烟台264001）

近年来，由于在图像处理，模式识别，联想记忆及优化问题等方面的潜在应用，神经网络系统（NNs）受到众多学者的广泛关注和研究[1-4]。众所周知，神经网络系统的诸多应用极大地依赖于其动力学行为，尤其是其平衡点的存在性和稳定性。而且，一方面由于放大器有限的转换速度和有限的信息处理速度导致时滞在神经网络系统中往往是不可避免的，甚至成为系统不稳定或产生震荡的一个重要根源。另一方面，有的神将网络系统可能并不具备人们所需要的动力学行为。在无时滞神经网络系统中引入恰当的时滞成为解决这些问题的方法之一，例如，Yang和Cao就将时滞映射神将网络系统用于求解二次规划[5]，Li将时滞神经网络系统用于求解凸规划并指出若能选择引入恰当的时滞，则可获得凸规划精确的最优解[6]。时滞神经网络系统的稳定性无论是在理论上还是在实践中都具有重要的意义。因此，关于时滞神经网络系统大量的稳定性研究成果，不管是时滞相依的，还是时滞独立的不断被提出[7-28]。由于含有时滞的相关信息，一般而言，时滞相依的稳定性条件要比时滞独立的稳定性条件具有更低的保守性，尤其是对于小时滞神经网络系统更是如此。于是，学者们更多地关注于寻求能使得时滞神经网络系统保持全局渐近或指数稳定的时滞最大允许上界（MAUB），大量具有更低保守性的稳定性条件被提出。然而，正如很多学者指出的，传统方式构造的Lyapunov-Krasovskii泛函对系统稳定性条件的保守性的降低所起作用已很小[14，16-17]；而最近，时滞分割技术则被有效应用于降低系统稳定性条件的保守性[18-28]。

鉴于此，本文将构造一个新的Lyapunov-Krasovskii泛函，利用时滞分割技术并结合使用自由权矩阵和Jensen积分不等式，更精细地估计Lyapunov-Krasovskii泛函导数的上界，以获取由线性矩阵不等式（LMI）表达的具有更低保守性的系统时滞相依全局渐近稳定性条件。在本文中，ℝn×m表示n×m实矩阵空间，上标T表示转置，X≥Y（X＞Y）表示矩阵X-Y半正定（或正定），其中的X和Y都是对称阵，In×n、On×n分别表示n×n维的单位阵和零矩阵，记号∗总用于表示对称矩阵以及sym(A)=A+AT中的对称块。

1 问题描述

考虑如下的定常时滞神经网络模型：

一般地，对激励函数作如下假设：

假设：激励函数gj(⋅)连续、有界且

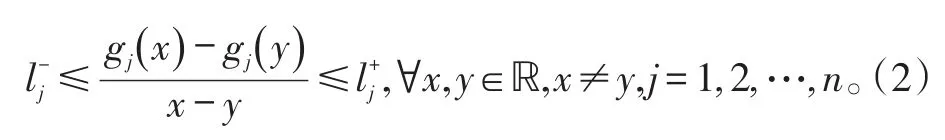
以上的假设能确保系统（1）存在平衡点

2 主要结果

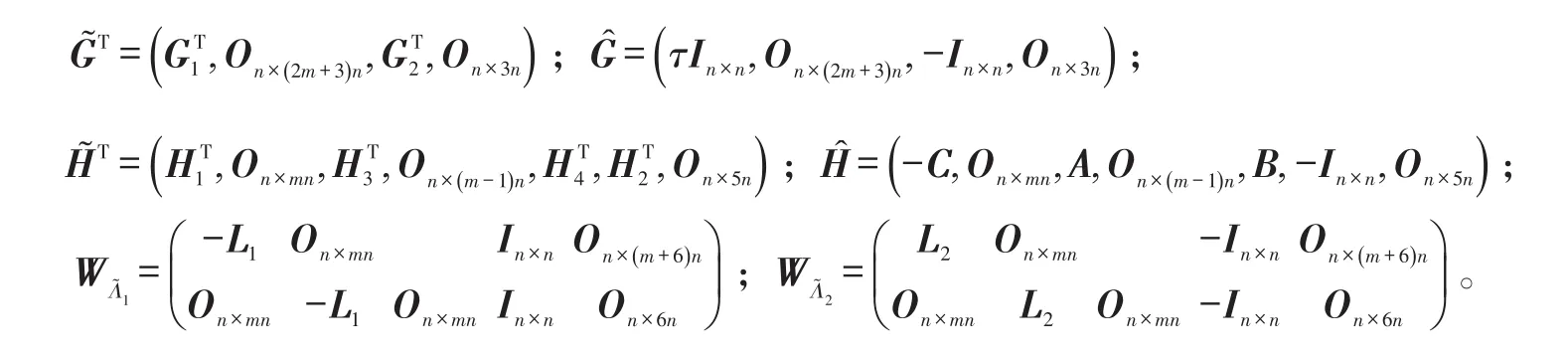
证明：由Brouwer不动点定理不难证明系统平衡点的唯一性，此处略。只证平衡点全局渐近稳定。为此，构造如下的增广Lyapunov-Krasovskii泛函

是(2m+8)n维行向量，矩阵Ξ如前定义。

由式（6）及引理2.2知，存在正数ε使下式成立：

从而，有V̇(t)≤ξT(t)Ψξ(t)＜-ε‖x(t)‖2。

这意味着系统（3）的平衡点全局渐近稳定，证毕。

注1：通过构造一个更具一般性的增Lyapunov-Krasovskii广泛函，定理3给出了一个时滞相依全局渐近稳定新判据，值得指出的是，这里V1(t)的第一项，V2(t)中的二重积分项，V3(t)中的三重积分项以及V4(t)都有别于相关文献，它们对降低稳定性判据中的保守性起着重要作用。

注2：时滞分割也是降低保守性的重要因素。随时滞分割数目的增加，保守性也随着降低。即便在分割数目m=1，即不分割时，下面的数值实例将说明本文结果也优于相关文献结果。

3 数值实例

例：考虑4阶时滞神经网络系统[7-8]，参数如下：

根据文文献[7-8]中稳定性判据，可计算得其时滞最大允许上界（MAUB）分别为3.584和3.589 8。而用本文判据，当时滞分割数目m分别取1、2、3、4、5时，相应MAUB分别为3.784 9，4.074 3，4.192 7，4.375 3和4.375 5，这说明了本文结果的有效性且显然是优于文[7-8]的结果的。但是由于矩阵变量P、Q（尤其是后者）的维数较大，这给计算带来较大负担，而且当m分别取3、4、5时，MAUB的改善并不明显。通过比较，为获得较满意的MAUB，这里取m=3更合适一些。