海杂波谱的机理及时变特性分析
2019-06-18王国庆刘宁波李雪腾
王国庆,丁 昊,刘宁波,李雪腾
(海军航空大学,山东烟台264001)
海用雷达面临的复杂海杂波背景严重限制了对海探测性能。研究海杂波特性认知技术,并建立海杂波模型是改进和创新雷达目标检测算法的基本前提[1-9]。在相参条件下,海杂波谱属于海杂波特性认知中重要研究内容之一,它是雷达相参处理、多普勒域海杂波抑制和动目标检测的基础。目前,对海杂波谱的研究主要集中在平均多普勒谱形状的分析和建模方面[10-13],有代表性的成果分别为Lee和Walker提出的模型[12-14]。当观测时间较长时,由海表面状态、风速风向等海洋环境参数变化引起的非平稳因素不可忽略。此时,海杂波谱也会表现出时变特性,对海杂波建模仿真、抑制及目标检测等问题都具有重要影响。
目前,专门研究海杂波谱时变特性的文献并不多见。为此,本文以岸基雷达海杂波数据为研究对象,在分析海杂波谱机理及现有研究成果的基础上,利用不同极化方式的IPIX雷达数据和某型雷达的实测海杂波数据,对海杂波谱的时变特性进行了分析,并研究了海杂波相关时间的统计特性以及谱宽与海杂波拖尾程度之间的关系。
1 海杂波谱机理分析
以岸基雷达海杂波为研究对象,对海杂波谱的形成机理进行简要分析。岸基雷达工作在对海模式时,天线主波束照射区域的三维示意图和侧视示意图分别如图1 a)、b)所示。图1中:γ和ψ分别表示俯视角和入射余角,考虑到海表面所受到的倾斜调制作用会导致雷达本身的水平线和波束照射表面的切线并不在同一方向,则这2个角度并不相等;θB表示雷达波束宽度;R表示天线位置和照射区域中心之间的径向距离;椭圆区域即为雷达天线波束照射到海表面的覆盖区域,又称为雷达脚印;ψ1、ψ2分别为照射区域前后两边界点的局部入射余角。
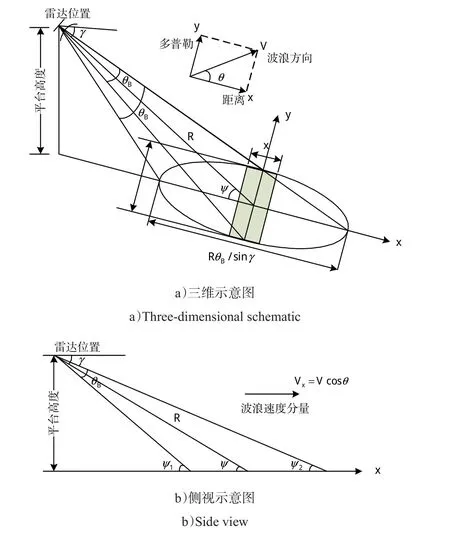
图1 雷达主波束照射区域示意图Fig.1 Schematic diagram of radar main beam illumination area
假定照射区域内海表面波浪的方向和速度V均保持不变,波浪方向相对于波束入射面的方位角为θ。对于相参雷达,海表面散射体与雷达天线之间的相对运动会导致海杂波的相位在脉冲之间变化,这种相位变化可以用多普勒中心频率fD等价表示为
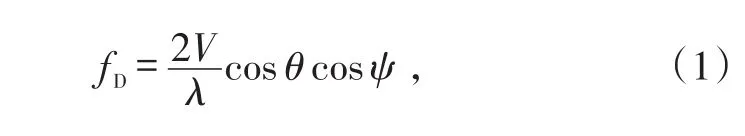
式中,λ为雷达工作波长。
同时,天线波束宽度会引起海杂波谱的展宽,即多普勒谱宽,其表达式为:
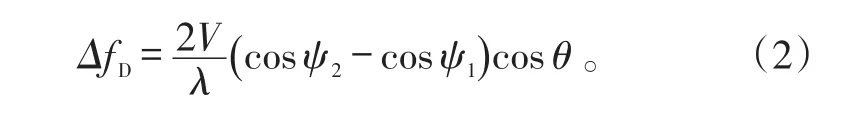
由图1中的几何关系可知:
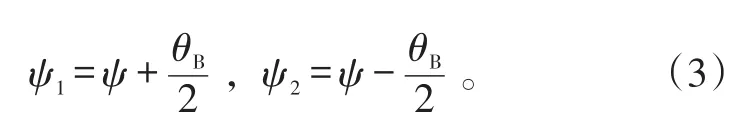
当天线波束较窄时,式(2)可以等价为:
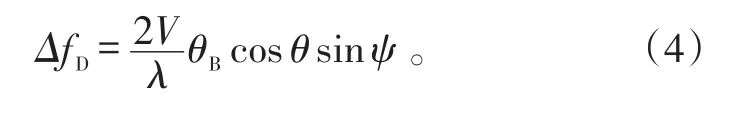
可以看出,波浪速度越大、雷达波长越短、电磁波前后边界的局部入射余角变化越大,则多普勒效应引起的海杂波谱展宽就越大。
由式(1)和式(4)可知,海杂波的多普勒中心频率和谱宽随雷达的工作频率λ而变化,即:
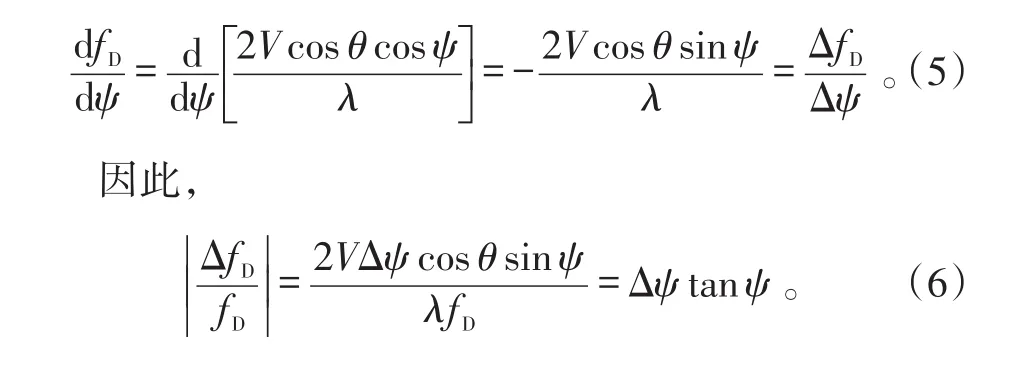
式(5)、(6)中,Δψ=ψ1-ψ2=θB。
由式(6)可知,以多普勒中心频率对谱宽进行归一化后,得到的展宽系数仅取决于天线的波束宽度θB和入射余角ψ,与雷达工作频率和波浪的相对方向均无关。
图2分别给出了天线波束宽度为1°和5°情况下海杂波谱的展宽系数与入射余角之间的关系。可以看出,在天线波束宽度一定的条件下,多普勒谱相对于中心频率的展宽程度随入射余角的增大而增大,这主要由波浪速度在雷达波束入射方向的投影变大所引起。当波束宽度减小时,谱的展宽程度有所下降。
在低入射余角情况下(即入射余角低于平均海表面倾角,约为10°),由天线波束宽度引起的多普勒谱展宽程度很小,且天线波束宽度越小,对谱宽度的影响也越小。因此,由天线波束宽度引起的海杂波谱展宽很小,基本上可以忽略不计。
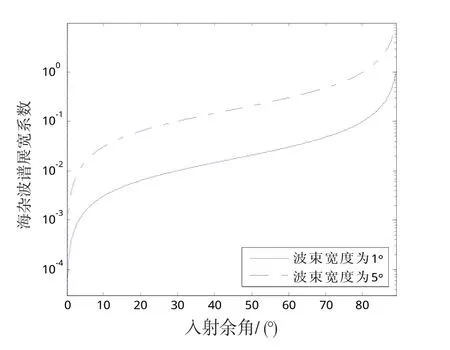
图2 谱的展宽程度与入射余角之间的关系Fig.2 Relationship between the degree of broadening of the spectrum and the incident residual angle
图3分别给出了IPIX雷达实测海杂波在HH、VV极化模式下的多普勒谱估计结果,数据描述在第3节给出。由图3可知,多普勒谱的中心频率为负,表明海浪正在向远离雷达的方向运动。多普勒谱宽、中心频率等参数对极化方式具有敏感性,表明不同极化方式下占据主导作用的散射体类型并不相同[12,14-15]。
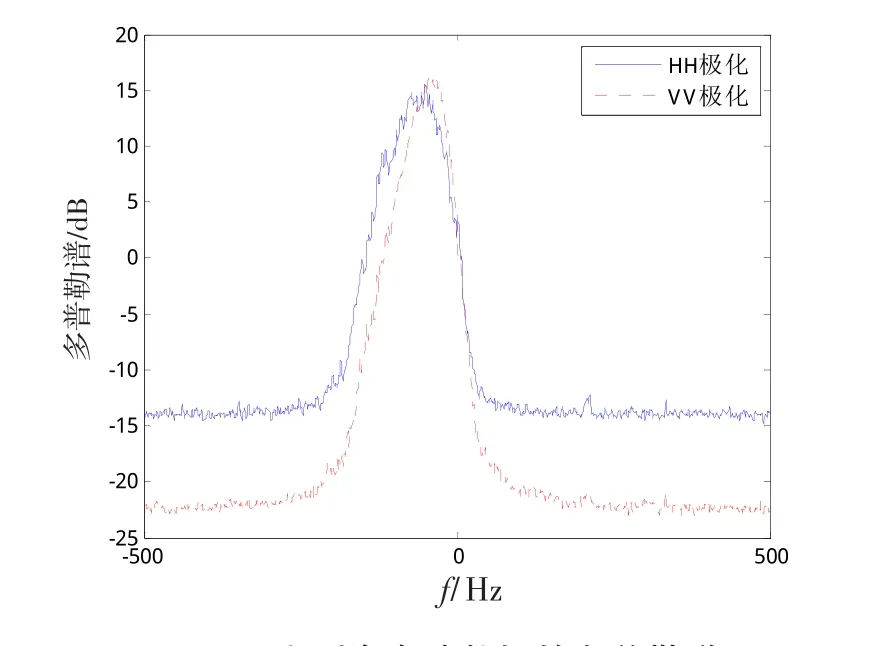
图3 实测海杂波数据的多普勒谱Fig.3 Doppler spectrum of measured sea clutter data
由于海表面状态、风速风向等海洋环境参数随时间而变化,当观测时间较长时,海杂波谱也会表现出时变特性,即海杂波具有非平稳性。海杂波谱时变特性的研究对于海杂波谱的建模、海杂波抑制以及目标检测等问题都具有重要的意义。Gini等[16]已经在相关文献中研究了海杂波谱的时变特性对协方差矩阵估计和恒虚警检测算法的影响。此外,文献[17-18]以VV极化数据为例,对海杂波谱的时变质心、谱宽随纹理分量功率的变化关系等问题展开研究,建立了3阶时变AR模型,以揭示长波对Bragg波的调制作用。
2 实测数据描述
采用2种不同极化、不同波段的实测海杂波数据进行后续研究。#1数据来源于“Osborne Head Database”,测量平台为加拿大McMaster大学的X波段IPIX雷达。本文采用1993年在加拿大新斯科舍省南部城市Dartmouth的测量数据。试验时,雷达从峭壁上俯视大西洋,纬度/经度为44°36.72'N/63°25.41'W,架设高度距平均海平面约30 m。试验时,采用的雷达参数如表1所示。在驻留模式下,数据采样时长约为130 s。本次试验公开了14组驻留模式数据,其中4组数据受到截断效应的严重影响(编号分别为#18、#19、#25和#283)。因此,可用数据共10组,每组包含14个距离单元。
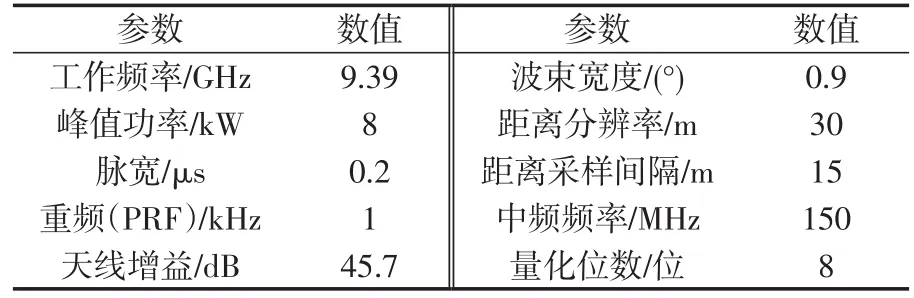
表1 IPIX雷达参数Tab.1 IPIX radar parameters
#2数据是采用自行研发的雷达中/视频数据采集器采集得到的海杂波数据,试验雷达架设于固定平台上,数据采集期间雷达天线工作在驻留模式,即天线在水平和俯仰方向上固定不动,距离向采样率为10 MHz,风力约为5~6级,北风,海况约为5级。图4分别给出了3组实测数据的时域归一化幅值,由于雷达参数、海洋环境参数等因素存在差异,海杂波时域信号的功率水平、起伏方式以及非高斯程度等特征均不相同。
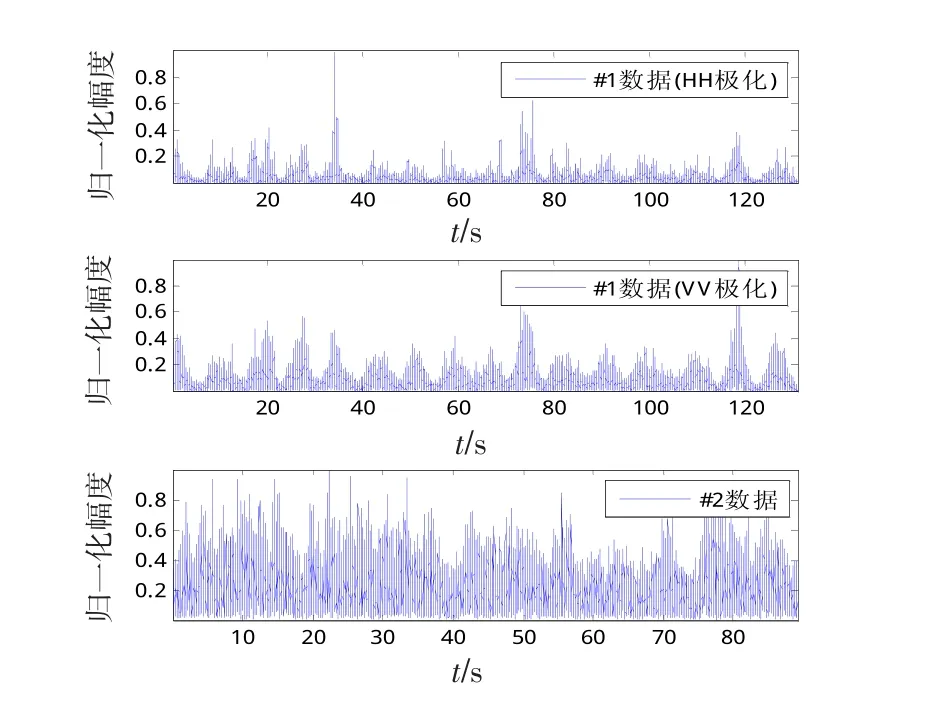
图4 实测数据的归一化幅值Fig.4 Normalized amplitude of the measured data
3 谱的时变特性分析
3.1 谱估计方法
在分析谱的时变特性时,首先,对数据进行分段,并估计出每段数据的多普勒谱。由相关文献的研究结果可知,当数据段的持续时间小于重力波周期时,海杂波的局部功率水平接近于常数,海杂波可以看作近似平稳的随机信号。为此,在数据分段时须考虑海杂波数据的相关时间,并同时兼顾每段数据的长度以提高谱估计的分辨率。
谱估计方法采用加窗的周期图法,窗函数为Blackman窗。以#1数据为例,其平均多普勒谱已经在图3中给出。图5分别给出了3组海杂波数据的时间-多普勒谱,显然,不同数据的时变谱特征(如谱峰频率、谱宽等)具有明显差异,#2数据的时变谱展宽现象较为严重,这可能与采集数据期间海况较高有关。
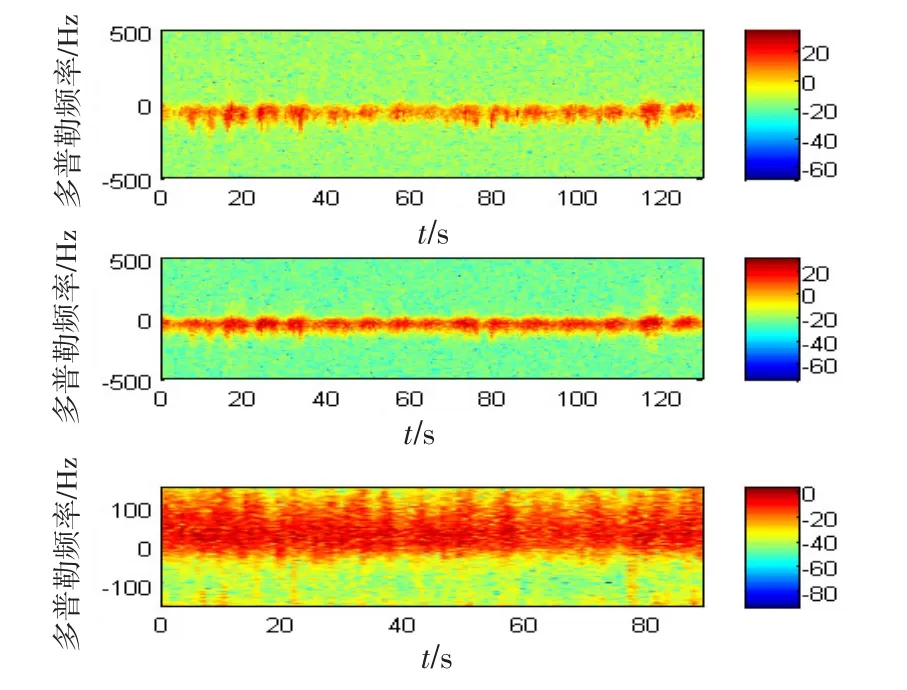
图5 海杂波谱估计结果Fig.5 Estimation results of the sea clutter spectrum
3.2 时变参数的分析
3.2.1 相关时间的统计分析
由维纳-辛欣定理可知,对于任意的平稳随机信号,其自相关函数和功率谱之间互为Fourier变换的关系,而协方差矩阵也是由自相关函数经过变换构造得到。因此,谱、相关函数和协方差矩阵之间具有一一对应的关系。通过相关性分析,可以从时域的角度揭示海杂波谱的一般变化规律。对相关函数进行归一化得到相关系数,当相关系数的取值从1衰减为1/e时,可以近似认为海杂波不再相关。此时,对应的时间延迟称为海杂波的相关时间。本节主要分析相关时间的统计特性。
对于任意一段海杂波数据,相关系数的估值公式为:
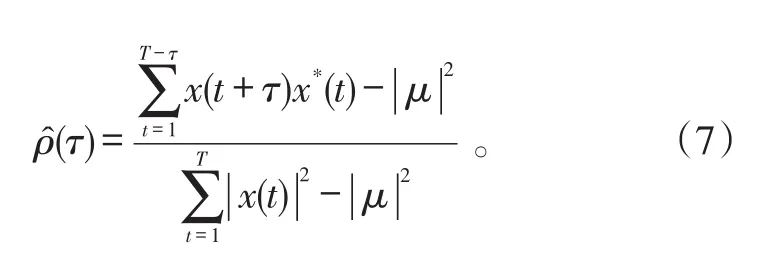
式(7)中:μ表示海杂波均值;()*表示复数共轭运算。
分别估计每一段数据的相关时间,并得到相关时间的直方图如图6所示。可以看出,对于#1数据,VV极化的相关时间更加离散,且明显比HH极化的相关时间要长,这表明,HH极化的海杂波谱展宽效应更加明显。
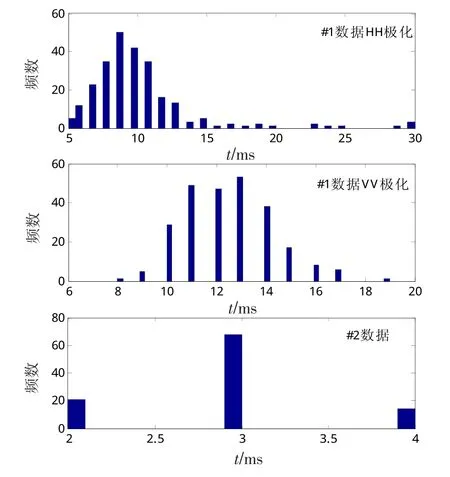
图6 相关时间的统计分析Fig.6 Statistical analysis of relevant time
通过图7可以更加直观地反映出上述结论,谱宽的时变特性非常明显,且2种极化数据的谱宽出现峰值的时刻基本一致。同时,谱宽随时间的变化表现出一定的周期性,这可能与海浪的周期性起伏有关。#2数据的相关时间更加离散,这与其时变谱的快起伏变化相对应。#1和#2数据存在诸多差异,因而分析结果不能直接进行比较。
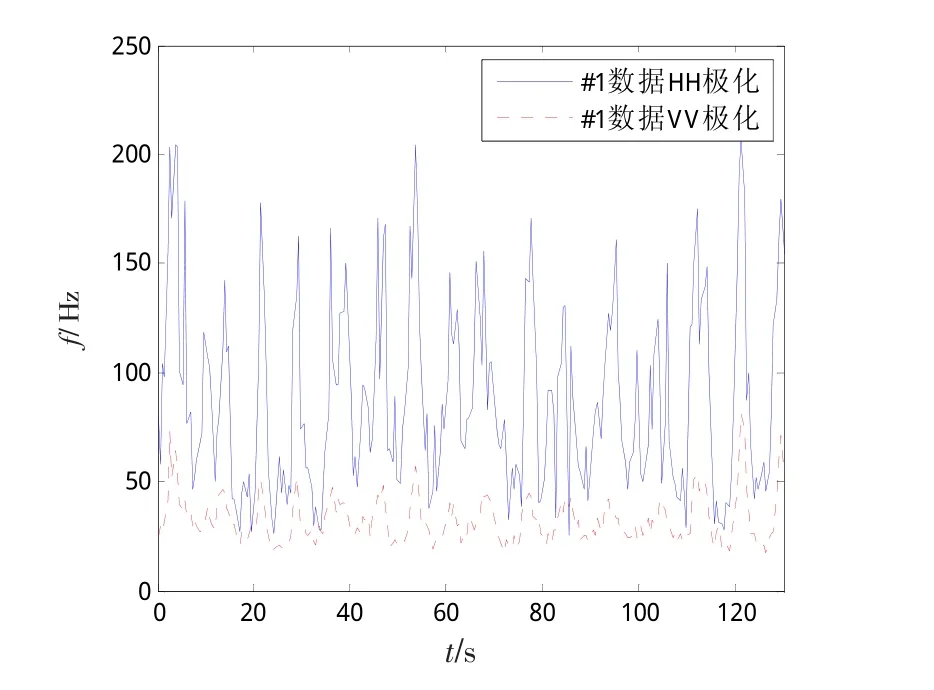
图7 #1数据谱宽的时变特性Fig.7 Time-varying characteristics of the spectrum width of data#1
3.2.2 谱宽与海杂波拖尾程度的关系
Ward认为[19],海杂波统计特性的拖尾程度可能与谱宽有关,其机理在于:多普勒谱较宽时,在大部分多普勒门内都具有较大的归一化方差,因而谱宽应该和海杂波的拖尾程度相联系,海杂波越尖锐,则谱越宽。然而,Lamont等人通过对海浪池采集数据分析发现[15],在某些方位上,海杂波具有较窄的谱,但是其拖尾程度却明显高于具有较宽谱的海杂波。显然,这是一种相互矛盾的结论,且目前没有形成统一的观点。本节利用现有的实测数据,对两者之间的关系进行初步分析。海杂波的拖尾程度采用峰度(γk)来衡量,如果海杂波的拖尾程度高于高斯分布,则峰度大于0,峰度越大,拖尾和冲激特性越明显。3组数据的分析结果分别如图8所示,由于谱宽和峰度的量级并不完全相同,为了便于分析两者之间的关系,在分析结果中对峰度进行了适当的放大。可以看出,谱宽和峰度的时变特性并不完全一致,在一些特定的时间段内,两者同步变化,出现峰值的时刻基本相同,这可能与快散射体的随机出现有关。因此,谱宽和海杂波拖尾程度之间并不存在明确的依赖关系。
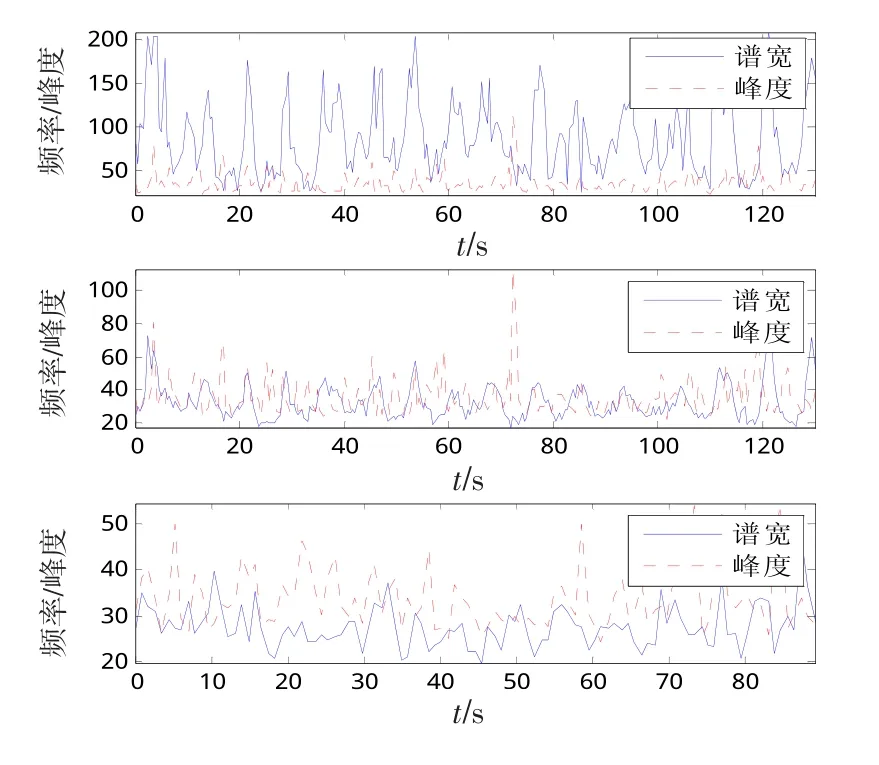
图8 谱宽和峰度之间的关系Fig.8 Relationship between spectral width and kurtosis
4 结束语
本文在分析岸基雷达海杂波谱的机理及现有海杂波谱特性研究成果的基础上,利用实测数据对海杂波谱的时变特性进行了分析,结果表明:VV极化海杂波的相关时间分布更加离散,且明显比HH极化的相关时间要长;HH、VV极化数据的谱宽出现峰值的时刻基本一致,且谱宽随时间的变化表现出一定的周期性;谱宽与海杂波拖尾程度的时变特性并不完全一致,因而并不存在明确的依赖关系。
海杂波谱的时变特性包含了丰富的研究内容,如谱的中心频率随海杂波功率水平的起伏关系、谱的归一化二阶强度矩特性等。由于篇幅限制,本文仅分析了部分内容,下一步将结合多种条件下的实测数据进行更为全面的分析。同时,将分析结果与海杂波抑制和目标检测算法相结合是另一个须重点解决的问题。
