基于DTW算法的参数缺失时的核动力系统故障诊断技术

赵 鑫，蔡 琦，王晓龙

(海军工程大学 核科学技术学院，湖北 武汉 430033)

随着以太网在核动力系统上的应用，核动力系统运行期间的各类监测参数可通过相关网络实时获取，因此数据驱动的核动力系统的故障诊断成为今后的发展趋势，而由于设备之间的干扰和网络传输的错误导致部分监测参数出现随机缺失，目前对监测数据完备情况下的故障诊断相对成熟，其对应的算法有支持向量机、时间序列、神经网络等[1-3]，对监测参数出现随机缺失的实时故障诊断研究较少：文献[4]采用了集成学习的概念，通过对基分类器的互补优势提升参数缺失情况下的诊断精度；文献[5]使用朴素贝叶斯和EM算法从缺失数据容忍和修复两个角度对数据进行预测，提高了历史监测数据随机缺失情况下的目标函数预测；文献[6]采用了多元动态时间弯曲(DTW, dynamic time warping)算法对多维时间序列进行模式匹配，对完整的事故过程具有较好的匹配效果。

上述研究为缺失数据下的故障诊断与模式识别，主要分为两大类，一类是对缺失数据采取了修补的措施，其又可分为均值填补、回归填补等固定填补方式以及构建支持向量机、EM算法等动态填补模型的方式[7]；另一类是缺失参数采取策略，通过构建多个诊断模型进行诊断结果的互补或采用DTW算法对数据直接进行相似度比较[8]。由于核动力系统的监测参数具有高维度和非线性的特点，传统方式填补后的诊断效果不理想，动态填补模型如贝叶斯模型的构建需要一定量的数据作为支撑，而核动力系统故障工况的小样本特点导致了该方案可行性较差。为此，本文基于多元DTW[9-10]算法，提出滑动时间窗口的距离匹配模型，寻找目标模式之间的最小距离，通过选取合适的窗口大小和监测参数减小DTW匹配模型的复杂度，提高匹配模型的计算速度，用于核动力系统监测参数随机缺失下的实时故障诊断。

1 DTW算法的基本原理

DTW算法优化了特征参数错位所产生的影响，基本原理是寻找两个时间序列之间的最优弯曲路径，序列中的数据点根据坐标值去匹配另一条序列中最具相同特征的点，数据点的距离和即为最优弯曲距离的累加和[11](图1)。

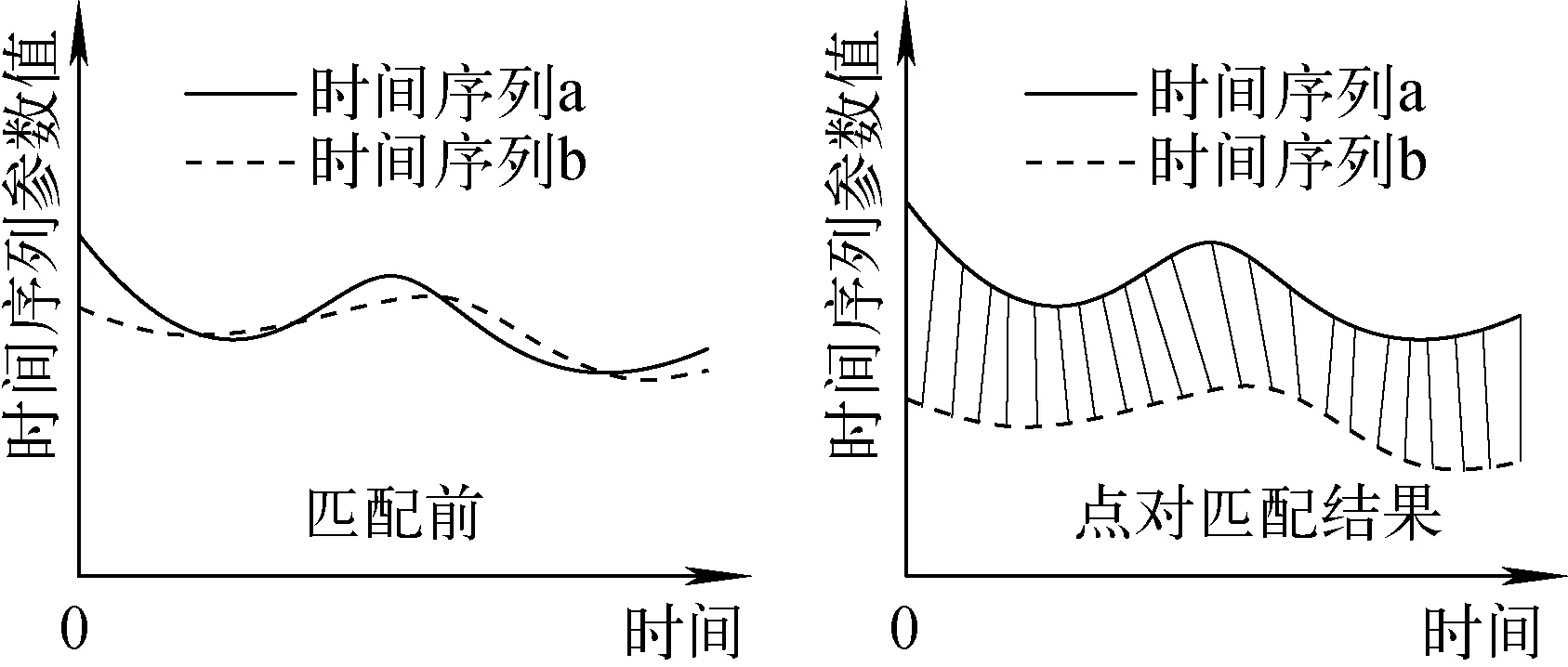
图1 DTW算法的基本原理Fig.1 Fundamental principle of DTW algorithm

假设有两个长度不同的时间序列X=(x1,x2,…,xm)、Y=(y1,y2,…,yn)，其中，m、n分别为两条时间序列的长度。根据两条时间序列的坐标构造成1个m×n的距离矩阵Am×n：

(1)

在距离矩阵Am×n中，元素aij是通过xi和yj坐标距离的计算得到的，其计算过程为：

aij=‖xi-yj‖w

(2)

当w=2时为2-范数，即欧式距离。

而两条时间序列的DTW距离是通过Am×n寻找1条距离最小的弯曲路径pmin：

pmin={p1,p2,…,pd,…,pk},

k∈{max(m,n),m+n+1}

(3)

其中，设pd为搜索至点aij时，弯曲路径的当前累积距离。

该路径的寻找过程必须满足以下3个约束条件。1) 路径起始点固定：搜索路径的起点为a11，终点为amn。2) 路径的单调性：设搜索的当前点为aij，当前累积距离为pd，pd+1=pd+ai′j′，则i′≥i，j′≥j。3) 路径的连续性：设搜索的当前点为aij，当前累积距离为pd，pd+1=pd+ai′j′,则i′≤i+1，j′≤j+1。根据上述3个条件，第1条确定搜索路径的起始点，第2、3条确定搜索路径的下一个点是当前点的上方、右方或右上方中的1个(图2)，其中当前点为pd，并假设此时正在搜索的当前点为aij，到下一个点pd+1的递推关系为：

pd+1=pd+min[a(i+1)j,a(i+1)(j+1),ai(j+1)]

(4)

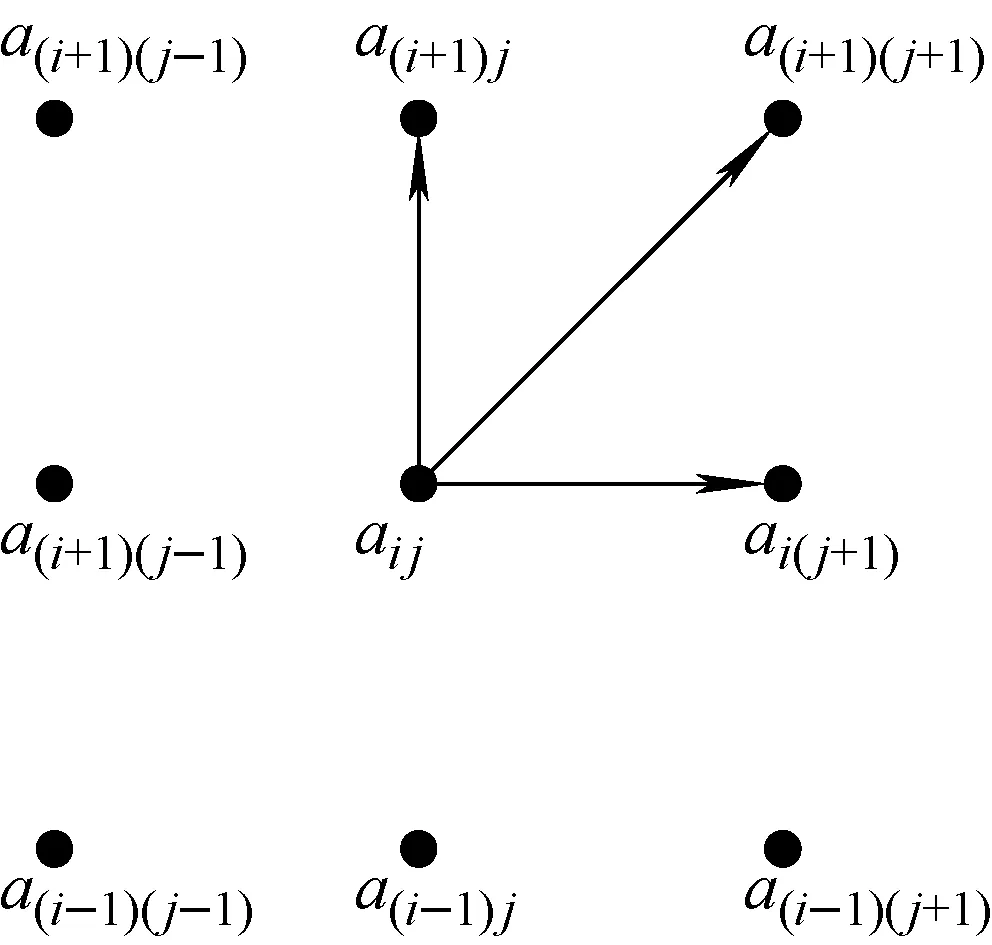
图2 pd到pd+1的递推关系Fig.2 Recursive relation between pd and pd+1

经计算，得到最终的计算结果pmin，为解决序列长度不同导致的累积距离存在差异性，需通过式(5)对累积距离进行平均化处理：

p=pmin/k

(5)

其中，p为平均后两条序列的累积距离。

在整个搜索过程中，根据3条约束条件，DTW算法遍历了两条时间序列中所有观测点，且两条序列中的每个点在另一条序列中找到相对应的点，但这也反映了该算法的计算量较大。

2 滑动窗口下的多元DTW算法的模式识别模型

当通过两个一维不等长时间序列的DTW距离去度量两个时间序列的相似度时，由于一维时间序列在监测过程中受到波动、噪声等因素的影响，对DTW的准确度会产生一定的影响，加之目前核动力系统监测数据具有高维度的特点，多元DTW算法的模式识别模型具有较强的鲁棒性和更高的准确率。

2.1 目标时间序列的处理

事故引入后，改变了系统稳定运行的状态，短期内系统的监测参数会产生较大的波动，由于波动的大小具有一定随机性，这会导致1条序列的顶点对应另1条序列的多个点，造成两条序列匹配点的畸形(图3)。为优化这种畸形匹配，需对时间序列进行平滑处理，将监测值与该状态之前的若干记录值取平均处理，将波动平摊至附近的若干点上，缺点是提高了计算的复杂度。

图3 平滑处理对DTW算法的影响Fig.3 Effect of smoothing on DTW algorithm

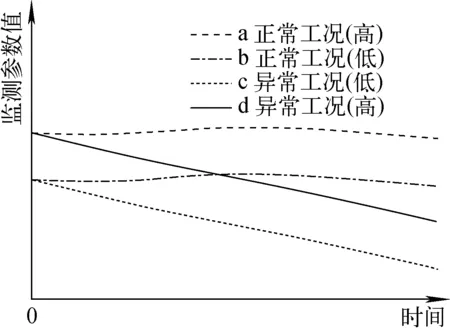
图4 不同初始运行条件对算法的影响Fig.4 Effect of different initial running conditions on algorithm

系统的监测参数与系统的运行状态有关，如图4所示，图中，a、b分别为系统正常运行时不同运行功率系统监测参数的运行变化，c、d分别为系统在低、高工况下发生异常时监测参数的变化。当系统在高工况正常运行状态a引入事故工况，而事故状态下监测参数如果具有曲线d向下波动的趋势，经过计算会发现时间序列c、d之间的累积距离大于d、b之间的累积距离，会造成d与b更接近的诊断结果，为解决该类型的误诊断问题，对标准时间序列进行归一化，计算公式为：

x标准=(x-xmin)/(xmax-xmin)

(6)

其中，在标准多元序列中任意一维时间序列X中，xmax为该维度中的最大值，xmin为该维度中的最小值，样本点x经式(6)计算后得到归一化值x标准。而对于待测序列则采用对齐稳态工况下监测值的归一化方法，计算公式为：

(7)

待测样本点x′使用式(7)得到x待测。其中，x标稳为标准序列稳定时的监测值；x待稳为待测序列稳定时的监测值。

2.2 多元DTW累积距离计算模型

目前针对多元时间序列的DTW算法主要分为两类。一类为将多维时间序列转化成一维时间序列，文献[12]则采用距离度量的策略进行多维时间序列的降维转化；将多元时间序列应用多维分段拟合，对每个拟合段求取总误差作为DTW的1个元素，再应用DTW算法进行累积距离的计算[13]。另一类为对每一维时间序列应用差分、归一化处理后，采用DTW算法计算时间序列每一维对应序列的累积距离，按一定的方式拟合计算累积距离得到最终计算结果[14]。

由于核动力系统的监测数据是随机缺失的，同一时刻的某一监测数据可能存在缺失情况，将多维度的监测数据转化为一维时间序列会产生对应监测参数错位的情况，加之计算每一维对应时间序列的累积误差更能说明两条时间序列的相似性，故本文采用第2类的多元DTW算法进行相似度拟合。

考虑到每种事故工况的监测参数有相对固定的变化趋势，设定事故发生后有明显变化的监测参数为该事故下的敏感参数。本文采用多元DTW算法进行累积距离计算时，选用事故发生后波动较大的几类监测参数构成多元时间序列。为此本文多元时间序列采用了每种事故工况参数变化最明显的前几类监测数据组合在一起构成标准多元事故序列，构建形式如图5所示。

最终筛选出由上述监测参数及差分数据组成的多元时间序列，计算两个多元时间序列中对应的每一维的DTW累积距离，每个一维时间序列的相似性越高，DTW的累积距离越小，对每一维时间序列累积距离求和即得到多元时间序列的累积距离。

在每个事故工况下，将上述敏感参数按照时间轴构成多元时间序列，作为模式识别的标准序列。将未知工况的多元时间序列保留上述监测参数，并计算差分数据，整理生成待测序列。通过待测多元时间序列依次与各类模式识别的标准序列计算得到DTW累积距离。由于累积距离越小则两条时间序列越相似，待测序列与累积距离最小的多元时间序列模式一致。

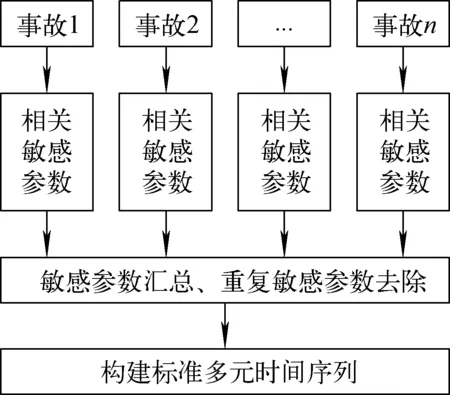
图5 标准多元时间序列参数的构建Fig.5 Construction of standard multivariate time series parameter

2.3 滑动时间窗口的动态故障诊断实时模型

本文假设原本完整的多元事故序列由于传输过程不稳定性造成了数据的随机缺失，导致原本等长的时间序列出现部分监测数值的缺失，通过DTW算法对不等长的序列进行模式识别。多元时间序列的模式识别模型对于进行实时的故障诊断存在两个问题：1) 实时的多元时间序列不能准确定位事故的起点，系统运行时监测数据是实时生成的，事故的引入时间点也是未知的，而事故的发生起点决定了待测多元序列的起点；2) 随运行时间的增长，多元待测序列的长度越来越长，随之而来的DTW算法的计算量不断增大，实时性诊断难以实现。如何定位事故的起点、减少计算的时间成为诊断模型的关键。

无线通信网络中，移动站和移动站之间、移动站和网络控制中心之间的信息传递都是通过无线信道来进行的。但是无线信道的开放性使得用户身份信息完全曝光在信道中，攻击者可以通过信道获得合法用户的身份信息，然后假冒合法用户身份进入网络，并假冒合法身份进行网络资源访问、使用通信服务，或者假冒网络端基站欺骗其他移动用户。

为解决DTW算法计算量过大的情况，本文通过构造滑动窗口DTW模型来简化运算量，具体步骤如下。

1) 实时获取核动力系统监测参数的运行数据，按照图5确定的敏感参数对获取的监测数据进行筛选，将t时刻的参数记为αt=(αt1,αt2,…,αtp)，其中p为监测敏感参数的数量。

2) 设定多元时间序列的长度为β，则记录t、t-1时刻，直至t-(β-1)时刻，并组成多元待测时间序列αtβ(其中p为多元时间序列的维度)：

(8)

如果序列中存在监测参数缺失，则用符号χ进行填充。

3) 对每个监测参数进行δ范围内平滑处理。对αtβ矩阵中每个元素的值由其本身及其前δ-1个时刻的原始监测数据取平均值得到，如果前δ-1个时刻监测值存在缺失，则将缺失值χ取0，缺失数据的个数记为η，计算公式为：

(9)

4) 将已知事故工况下的多元时间序列按照步骤1～3得到标准DTW多元事故序列，设该标准时间长度为B，与待测时间序列不同，B≫β。

5) 对于1条已知的事故标准序列，从事故起点依次滑动选取长度为β多元序列，与待测序列αtβ应用多元DTW算法计算累积距离，如果出现监测数据缺失的符号χ，则直接跳过该符号，比较两条不等长的时间序列，该事故工况下计算的次数ε为：

ε=B-β

(10)

φt=(φ1,φ2,…,φε)

(11)

其中：待测序列φε为第ε次的累积距离；φt中最小值φtmin即为待测多元序列在t时刻的最小累积距离。

6) 应用步骤5依次计算待测时间序列与其他事故标准多元时间序列的最小累积距离。

7) 比较各事故得到的最小累积距离，待测时间序列应与产生最小累积距离值最小的事故标准事故序列中的某一段最为相似，与对应的标准事故模式相一致。

整个计算的模型结构如图6所示。

由于待测多元时间序列的长度β不需过大，事故发生后监测参数的变化会在待测序列中直接反映，通过滑动窗口进行距离匹配，在标准事故序列中不需要定位事故的起点。β是固定的，不会随着时间的推移增长，而不同的事故序列DTW的计算过程并不冲突，故步骤5、6计算采用并行计算的形式，对于单个事故序列长度B较长的情况，可对事故序列选取多个断点，同时计算累积距离，以满足实时性的要求。

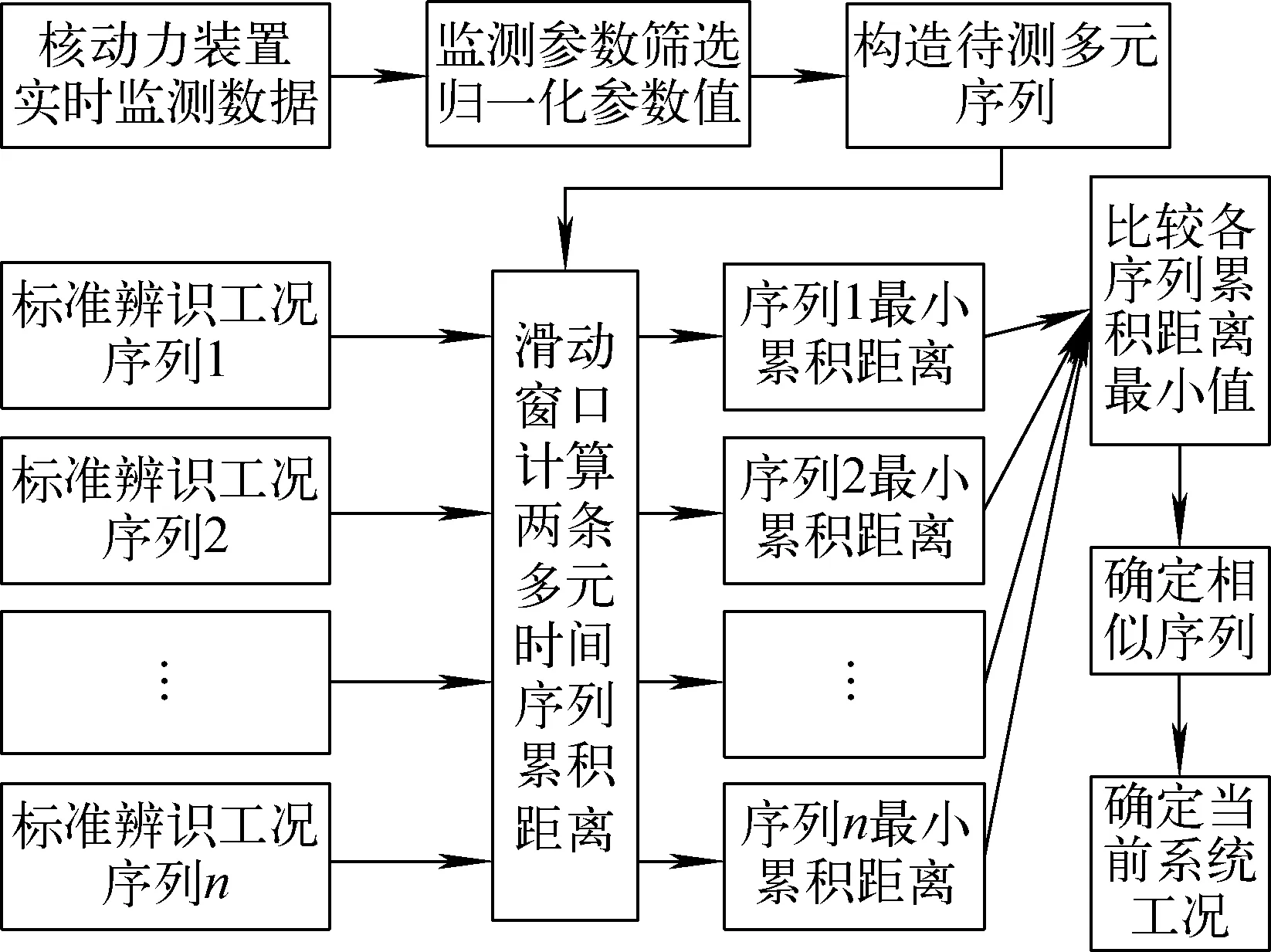
图6 滑动时间窗口的动态实时故障诊断模型Fig.6 Dynamic real-time fault diagnosis model of sliding time window

对于待测时间序列出现监测参数缺失的情况，使原本两条等长时间序列转变为不等长时间序列累积距离的计算，如果标准事故序列在采集过程中出现缺失，该算法同样可通过计算累积距离得到计算结果。

3 实例验证

本文为检验滑动时间窗口动态故障诊断实时模型辨识的准确性，选用了核动力系统一回路失水事故(右环路U型管破口百分比53%)、一回路失流事故(单环路两个主闸阀开度百分比50%)、二回路主蒸汽管道破口事故(右主蒸汽管道破口百分比11%)与正常工况(与上述事故工况发生前的运行状态相一致)进行实时在线监测，事故工况选取了中等严重程度。

3.1 故障诊断模型的构建

经过多次计算拟合，根据3类事故工况发生的基本原理，模型最终选用的敏感参数为：堆平均温度、稳压器压力、稳压器水位、稳压器温度、左右环路冷却剂流量、左右蒸汽发生器蒸汽流量、左右蒸汽发生器压力、左右蒸汽发生器水位，构建标准事故序列[15-16]。

与模型相关的其他参数值为：标准失水事故序列的长度为300，标准序列的失流事故长度为300，标准序列的主蒸汽管道破口长度为250，标准序列的正常工况长度为100，待测序列滑动窗口的长度为10，平滑处理参数δ为5。

3.2 故障诊断结果及分析

对模型的测试过程是在系统正常运行时投入事故工况，得到相关的监测结果。本文主要从两个角度对模型进行测试，一种为标准事故序列数据完整而待测序列数据出现缺失，另一种为标准事故序列数据出现缺失而待测序列数据同样出现缺失。通过实例进行测试，并对照了监测参数无缺失的情况。

待测多元时间序列选择系统正常运行时突发失流事故(单环路两个主闸阀开度为30%)，由于篇幅限制，部分监测参数的变化趋势如图7所示，并给出了监测参数未缺失情况下的诊断结果。

从故障诊断结果的角度进行分析，事故在25 s时引入，区域A为事故发生前，由于监测参数在事故发生前处于稳定状态，故无论是累积距离(图7b)还是最小累积距离出现的位置(图7c)的曲线都比较稳定，诊断结果为正常运行工况；在区域B，由于事故的引入，使系统运行状态从正常转为失流事故，故表征正常工况的最小累积距离不断增大，失流事故的最小累积距离不断减小，加上其他故障曲线的干扰，在25～35 s的诊断结果出现错误波动，35 s以后的诊断基本正确；在区域C中，由于事故的监测参数波动更符合失流事故的波动形式，故失流事故最小累积距离与其他事故的相比最小，故诊断结果为失流事故，而最小累积距离出现的位置也符合失流序列的发展过程，故图7c的失流事故曲线大致呈现直线增长的趋势，其斜率应与事故的严重程度有关，由于标准事故为50%开度，测试事故为30%开度，故斜率小于1；在区域D，由于超出了标准序列的测试长度，故在该区域的后期出现预测偏差。

在监测参数缺失率为10%的情况下，模型计算的累积距离及最小累积距离出现的位置曲线如图8a、b所示。在监测参数缺失率为10%、标准序列缺失率为10%的情况下，模型计算的累积距离和最小累积距离出现的位置如图8c、d所示，最终故障诊断结果如图8e、f所示。

从故障诊断结果的角度进行分析，事故在25 s时引入，各曲线的最小累积距离出现的位置的变化趋势大致与图7c相同，但随缺失数据的增加，诊断曲线的波动不断增大，原因在于DTW算法在比较不等长的时间序列时，会通过相邻点寻找最小的累积距离，此时的计算距离一般较参数完整情况下的大，进而导致了曲线的波动，但从计算的辨识结果看，曲线的波动对累积距离大小之间的比较影响较小，辨识结果并未产生错误。正常工况的最小累积距离曲线在事故发生后一直呈现不断增大的情况，这反映了事故工况下系统偏离正常状态逐渐增大。

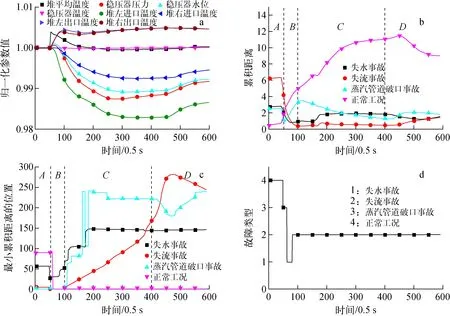
图7 完整数据下的故障诊断结果Fig.7 Diagnostic result with complete data

a、b、e——标准序列完整，待测序列缺失率10%；c、d、f——标准序列缺失率10%，待测序列缺失率10%图8 缺失数据下的故障诊断结果Fig.8 Diagnostic result with missing data

经过上述测试，该模型的诊断准确率较高，并且可对故障工况下的事故序列进行复盘和溯源分析。在计算量允许的范围内可添加其他事故的标准序列来拓展模型的辨识工况。

4 结论

通过计算和分析，证明本文提出的滑动时间窗口的动态故障诊断实时模型能以较高的准确率识别出事故工况的发生，对存在缺失的监测数据有较强的冗余能力，同时根据模式识别结果中最小累积距离出现的位置可进行多元时间序列的溯源，在标准事故序列中寻找到与当前系统最为接近的状态。该方法较好地平衡了DTW算法计算时间过长，发挥了算法在比较不等长多元时间序列的优势。对于模型中未考虑到的故障类型，可通过添加事故标准序列进行识别故障类型的拓展，为核动力系统在线运行支持提供了新的手段。