基于PLSR建模的地铁车站客流与周边用地关系分析

马超群，潘 杰，2，王 云

(1.长安大学 公路学院， 西安 710064; 2.南京市城市与交通规划设计研究院股份有限公司， 南京 210000)

交通与土地利用之间有着不可分割的关系。通常，交通设施的建设使得两地间或区域的可达性提高，人们愿意在交通设施附近或沿线购买房屋、建立公司或厂房，从而拉动土地利用的发展。同时，不同土地的利用形态又会要求和促进交通吸引产生量。长期以来，城市轨道交通规划的目标制定、方案设计和评价都体现了满足客运交通需求的理念，解决城市交通问题是城市轨道交通规划的核心所在。对于轨道交通沿线的用地形态和轨道交通客运量之间的内部联系，定性分析的研究较多，定量探讨的研究较少。因此，对城市轨道交通站点周边的土地利用形态与轨道交通客运量之间的关系建立模型，探讨其内部联系，具有重要的理论与现实意义。

美国亚利桑那州大学的Carol.M[1]采用TOD模式下的站点范围400～600 m，以凤凰城为例，研究轻轨对站点范围内都市交通、用地等的影响。Robert[2]认为轨道交通站点的土地利用密度、开发情况、多样程度，对轨道交通发展有着重要影响。Sumeeta[3]利用GIS研究了土地利用变化及其与城市轨道交通的关系，并分别从区域范围和局部范围建立了反映二者关系的模型。肖为周等[4]就轨道交通沿线土地利用变化对其客运需求的影响进行分析研究，对轨道交通沿线土地利用优化前后进行对比，分析优化用地对客运需求的影响，但仅从定性的角度对比分析，缺乏定量的计算分析。彭沙沙等[5]就轨道交通及土地利用协调发展方面，通过研究协调评价系统，有助于轨道交通线网合理规划和沿线土地合理开发。王淑伟等[6]就站点周边用地特性对轨道客流影响机理研究进行了线性分析，但是站点周边的用地内部存在相关性，而单纯的线性回归难以准确描述其内部联系。杨明等[7]就城市土地利用与交通需求之间的相互作用关系，研究了建立两步式土地利用与交通需求相关关系模型的方法。杨敏等[8]针对新建城区的特点引入区位因子，考虑人口和土地利用与交通生成的关系建立预测模型。

针对上述问题，本文利用PLSR方法建立土地利用形态和客流量间的关系模型，解决各种土地利用形态间的多重共线性问题，得到精度较高的回归模型，用于车站客流的测算估计。

1 PLSR建模基本原理

1.1 基本原理

偏最小二乘回归法(partial least squares regression,PLSR)是一种多因变量对多自变量的回归建模方法[9]。在普通的最小二乘回归的应用中，当自变量和因变量之间存在多重相关性时，将会严重危害参数估计，扩大模型误差，并破坏模型的鲁棒性。这是因为在最小二乘法下，回归系数的估计值是：A=(X′X)-1X′Y，当X中的变量完全相关时，(X′X)是不可逆矩阵，回归系数将无法求得；而当X中的变量存在高度相关关系时，行列式|X′X|的值接近于零，回归系数容易受较大舍入误差的影响，甚至出现与实际情况相悖的结果。PLSR方法则不直接考虑因变量总体与自变量总体的回归建模，而是在自变量的系统中提取了若干的对系统具有最佳解释能力的新的综合变量，然后在此基础上，利用它们进行回归建模。PLSR集多元线性回归分析、典型相关分析和主成分分析的特点，较好地解决了变量之间存在多重相关性或样本点数过少的回归难题。

1.2 多因变量偏最小二乘回归模型

多因变量最小二乘回归是多个因变量对多个自变量建立的回归模型[10]。设有q个因变量Y=(Y1,Y2,…,Yq)和p个自变量X=(X1,X2,…,Xp)。多变量PLSR的目的是寻找一个成分集合，用它对所有的因变量Y建立一个好的线性模型。模型如下：

k=1,…,q

(1)

式中：Ti被称为潜在变量或成分，每个成分T1,…,Th都是自变量X的线性组合。对模型中的每个因变量Yk都有相同的成分T1,…,Th，只是它们的回归系数不同。

假设对因变量Y=(Y1,Y2,…,Yq)和自变量X=(X1,X2,…,Xp)观测了n组数据，记为：

它们的均值分别为：

对Y和X做中心化处理。经中心化处理后的数据矩阵分别记为：

F0=(F01,F02,…,F0q)

E0=(E01,E02,…,E0p)

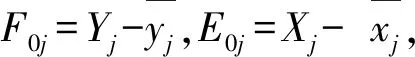
其中l为n维单位向量。

此处，成分Ti按如下步骤确定：

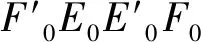
2) 通过迭代确定其余成分。假设已经确定了Ti，E(i-1)j，F(i-1)k，以及相应的样本值ti，e(i-1)j，f(i-1)k，现确定成分Ti+1。首先确定Eij，Fik。Eij为当E(i-1)j对Ti做回归时的残差，Fik是当F(i-1)k对Ti做回归时的残差，即：

(2)

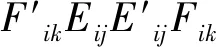
ui+1=Fici+1

(3)

再使用单因变量PLSR方法，由ui+1，e01，…，e0p来构造成分Ti+1。

在成分Ti，…，Th都被确定后，利用式(1)对每个变量Yk建立回归模型，参数β可使用普通最小二乘法估计。

1.3 模型的检验

用变量投影重要性指标来度量，自变量X对因变量Y的解释能力，也就是各土地利用形态指标Xj对地铁客流产生量Y的贡献大小。

(4)

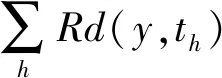
2 基于PLSR轨道交通车站客流模型

2.1 变量选取

2.1.1因变量选取

2.1.2自变量选取

自变量是能够对轨道交通车站进出站客流量产生影响的因素。相关研究已经表明，混合用地能在很大程度上影响轨道站点的乘降客流量。考虑轨道交通车站周围用地的复杂性，现有研究中应用较为广泛的混合用地指标，其最重要的影响因素即熵指数(社区内用地类型的多样性)，因此选取居住用地(X1，m2)、行政办公用地(X2，m2)、商业金融用地(X3，m2)、文化娱乐用地(X4，m2)、医疗卫生用地(X5，m2)、教育科研用地(X6，m2)、公共绿地(X7，m2)、市政用地(X8，m2)、停车场(X9，m2)、文物古迹(X10，m2)10个表征用地性质的指标和建筑容积率(X11)、建筑密度(X12)2个表征用地开发强度的指标，共12个自变量[11]。

2.2 模型标定

2.2.1数据获取

本文以西安市已运营的部分地铁车站为样本，选用了玉祥门、五路口、安远门、会展中心、开远门、钟楼、大雁塔、青龙寺、太白南路、北大街、小寨、通化门等12个车站。利用各车站的AFC数据进行统计分析，得到每个车站任何时段内的进站客流与出站客流。通过ArcGIS对西安市用地现状图进行处理，得到车站800 m半径范围内的用地指标。

2.2.2相关关系系数

通过数据相关性分析，得到地铁车站客流和12个影响因素之间的相关系数，见表1。可以看出，各变量间存在严重的多重相关性，如商业金融用地与建筑容积率，商业金融用地与建筑面积，相关性分别达到0.75，0.79。用方差膨胀因子法进行诊断，也可获得同样的结果[12]。

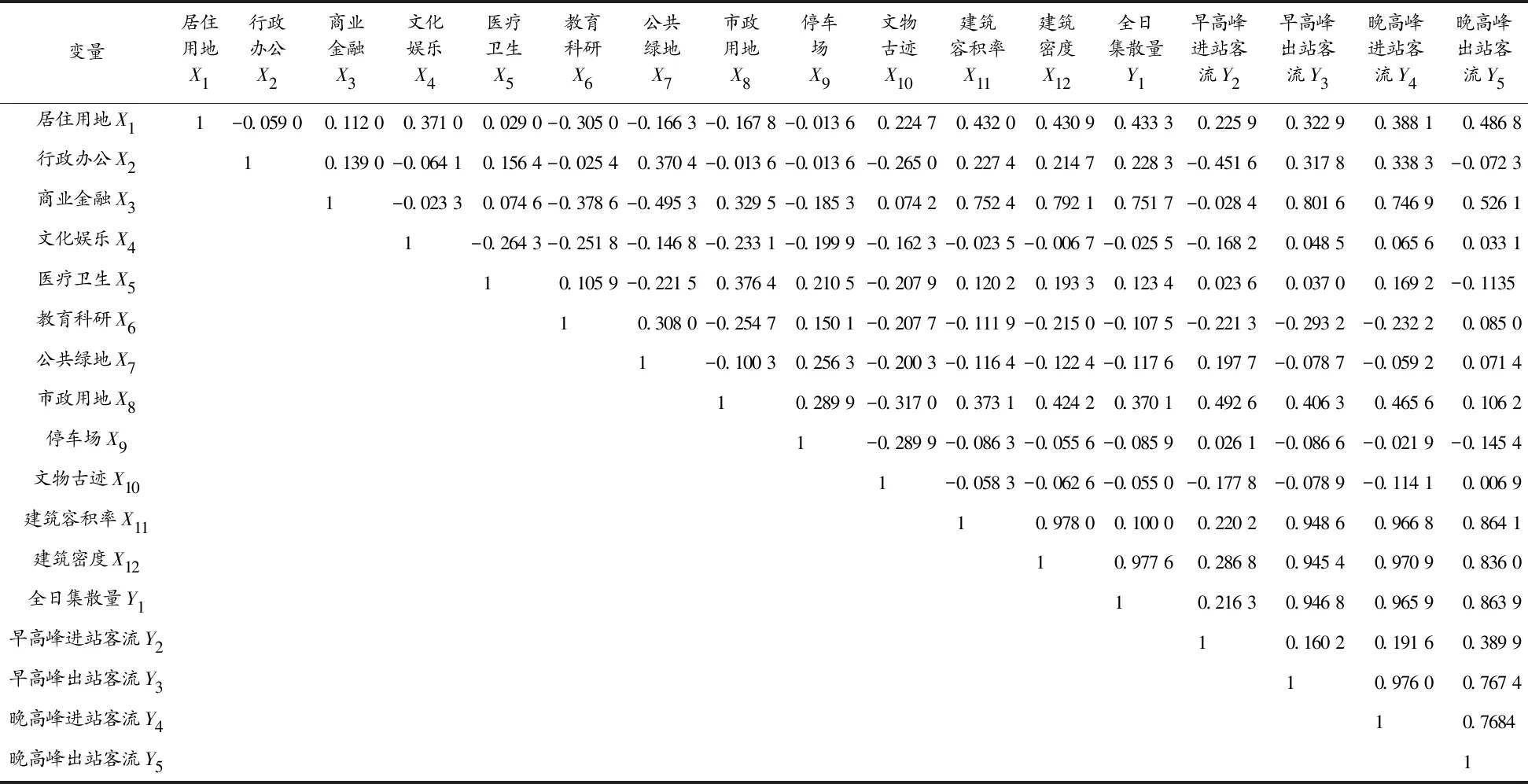
表1 变量间相关关系

2.2.3偏最小二乘回归方程的确定

利用Matlab软件，对自变量和因变量进行多因变量偏最小二乘回归分析，得到车站客流与12个自变量的标准化偏最小二乘回归模型。

按照标准化的逆过程，将偏最小二乘回归方程进行还原，得到全日集散量：

[18]Wenzhou,which is to say almost everyone in Wenzhou,has a horror story about the financial crisis that struck in mid-2011.（2016-06-11）

Y1=-77 607+0.050X1+0.004X2+0.052X3+

0.001X4-0.021X5+0.010X6+0.016X7+

0.139X8-0.279X9-0.003X10+

38 477X11+61 796X12

早高峰进站客流量：

Y2=647.63+0.001X1+0.017 7X2-0.007X3-

0.001X4-0.001X5-0.000 5X6-

0.000 5X7+0.001X8+0.028X9+

0.002X10+322.86X11+ 858.08X12

早高峰出站客流量：

Y3=-6 360.3+0.003X1+0.002X2+

0.005X3+0.0003X4-0.000 5X5+

0.000 2X6+0.000 2X7+

0.012X8-0.019X9-0.000 1X10+

2 974.8X11+4 823.1X12

晚高峰进站客流量：

Y4=-3 930.8+0.002X1+0.001X2+

0.003X3-0.000 09X4-0.000 3X5+

0.000 02X6+0.000 3X7+

0.012X8-0.012X9-0.000 2X10+

2 022.6X11+3 328.5X12

晚高峰出站客流量：

Y5=-2 630.5+0.002X1-0.003X2+

0.000 7X3-0.000 2X4-0.002X5+

0.001X6+0.002X7+0.001X8-

0.016X9-0.000 3X10+

1 735.1X11+2 699.7X12

表2 模型的标准化系数

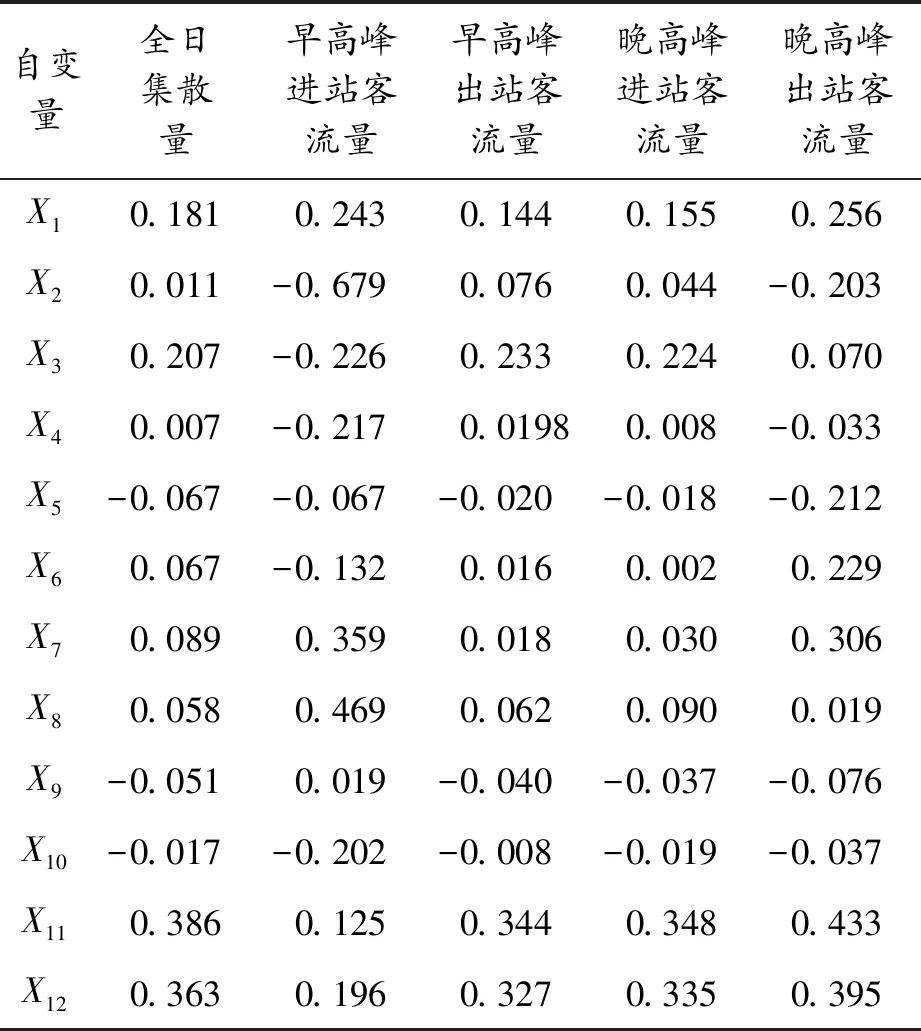
自变量全日集散量早高峰进站客流量早高峰出站客流量晚高峰进站客流量晚高峰出站客流量X10.1810.2430.1440.1550.256X 20.011-0.6790.0760.044-0.203X 30.207-0.2260.2330.2240.070X 40.007-0.2170.01980.008-0.033X 5-0.067-0.067-0.020-0.018-0.212X 60.067-0.1320.0160.0020.229X 70.0890.3590.0180.0300.306X 80.0580.4690.0620.0900.019X 9-0.0510.019-0.040-0.037-0.076X 10-0.017-0.202-0.008-0.019-0.037X 110.3860.1250.3440.3480.433X 120.3630.1960.3270.3350.395

3 模型分析与应用

3.1 车站全日集散量模型分析

根据式(4)计算变量投影重要性指标，计算结果如表3所示，数值的大小反映了变量对全日集散量的影响程度。投影变量重要性指标正负反映的是正相关影响和负相关影响。建筑容积率、建筑密度、商业金融、居住用地的变量投影重要性指标绝对值均超过1，其他变量投影重要性指标绝对值皆小于1，说明在本模型中，这4个指标是构成车站客流集散量的最重要影响因素。其中停车场、文物古迹与全日客流集散量成负相关。

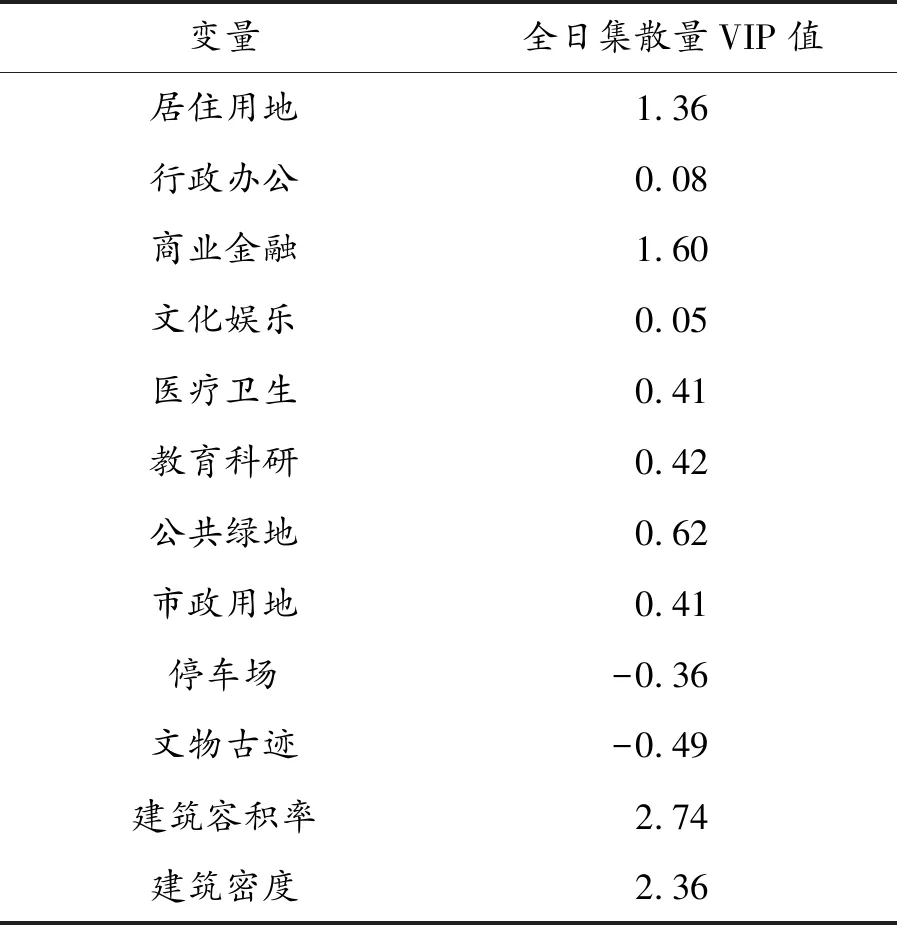
表3 全日集散量VIP值

将样本点的实测全日集散量与模型拟合集散量的结果进行对比，结果如图1所示。除个别车站外，模型拟合结果与实际值基本吻合。应用拟合模型计算西安地铁二号线的所有车站的全日客流集散量，并与实际值进行对比，如图2所示。模型拟合的精度整体良好。由于西安北客站属于地铁和高铁衔接的换乘站，乘降量受对外交通用地和铁路用地影响较大，本次模型选取车站，不存在此两类用地，故北客站的模型拟合较差。

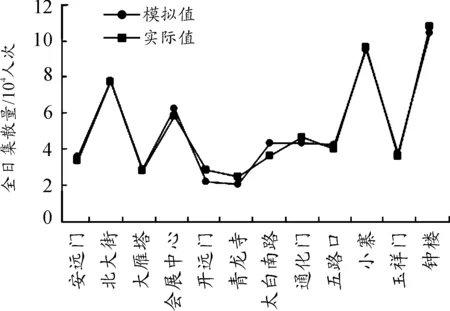
图1 全日集散量拟合结果

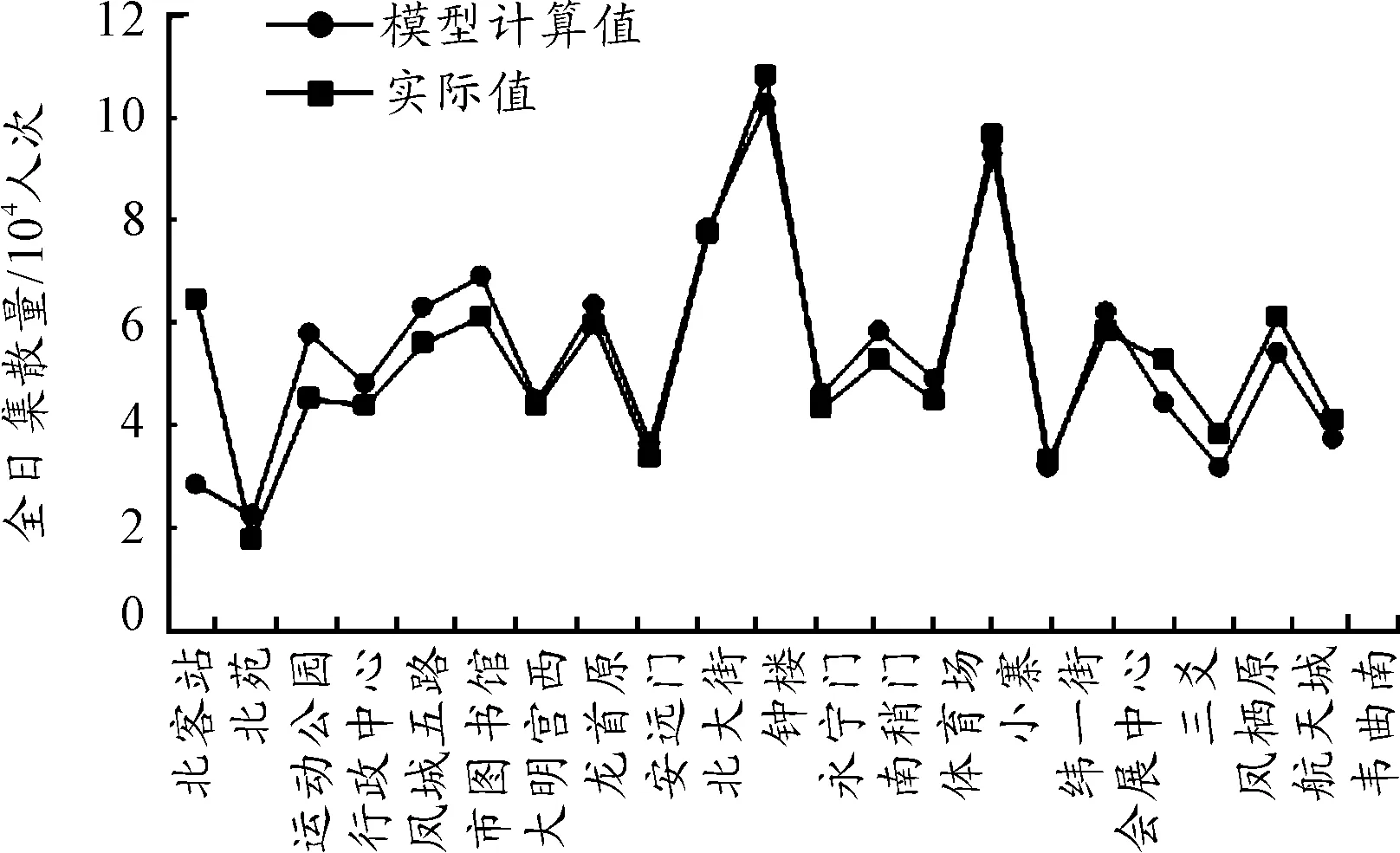
图2 全日集散量预测模型校验

3.2 早高峰进、出站客流量

早高峰进、出站客流量模型VIP值如表4所示。

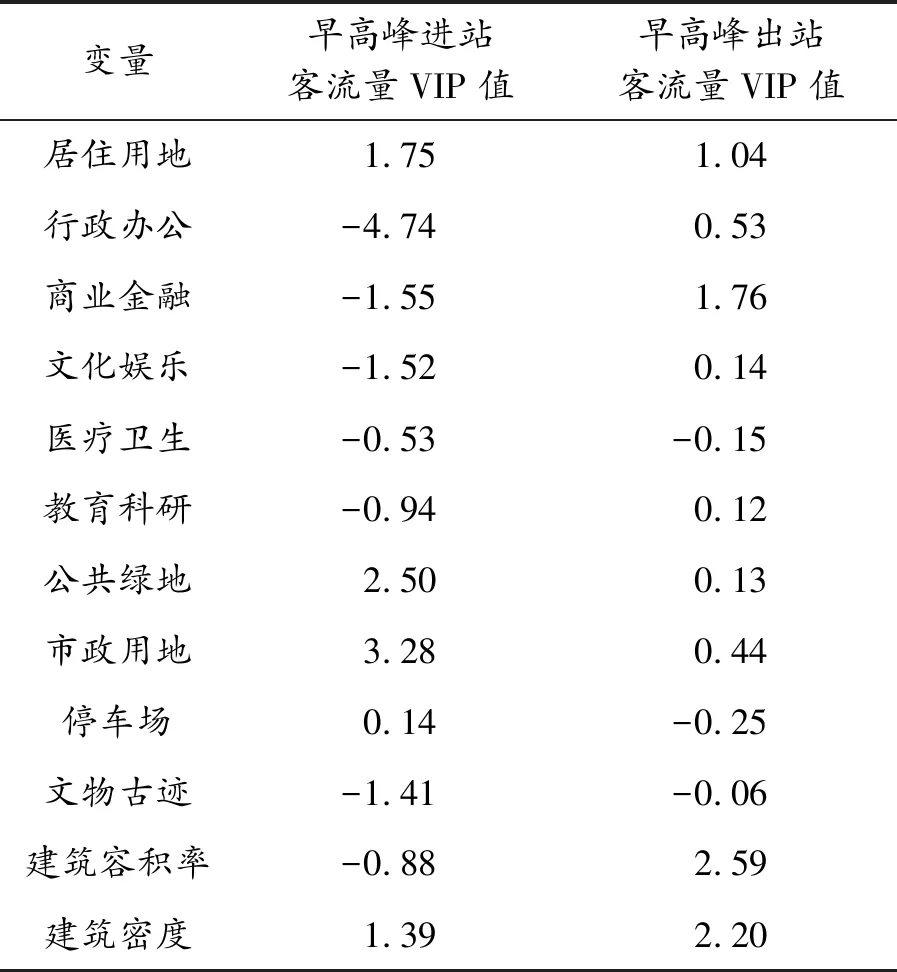
表4 早高峰进、出站客流量VIP值

对于早高峰进站客流量，居住用地、行政办公、商业金融、文化娱乐、公共绿地、市政用地、文物古迹和建筑密度的变量投影重要性指标绝对值均超过1，说明它们是构成早高峰进站客流量的最重要影响因素。早高峰进站客流多以上班、上学、通勤交通为主，行政办公、文物古迹、文化娱乐、商业金融这些类型用地多为早高峰出行的终点，属于吸引性质的用地，与进站客流量成负相关。

对于早高峰出站客流量，建筑容积率、建筑密度、商业金融、居住用地的变量投影重要性指标绝对值均超过1，说明这4个指标是构成早高峰出站客流量的最重要影响因素。

将样本点的实测早高峰进、出站客流量与模型拟合结果进行对比，如图3、4所示。除个别车站外，模型拟合结果与实测值基本吻合。

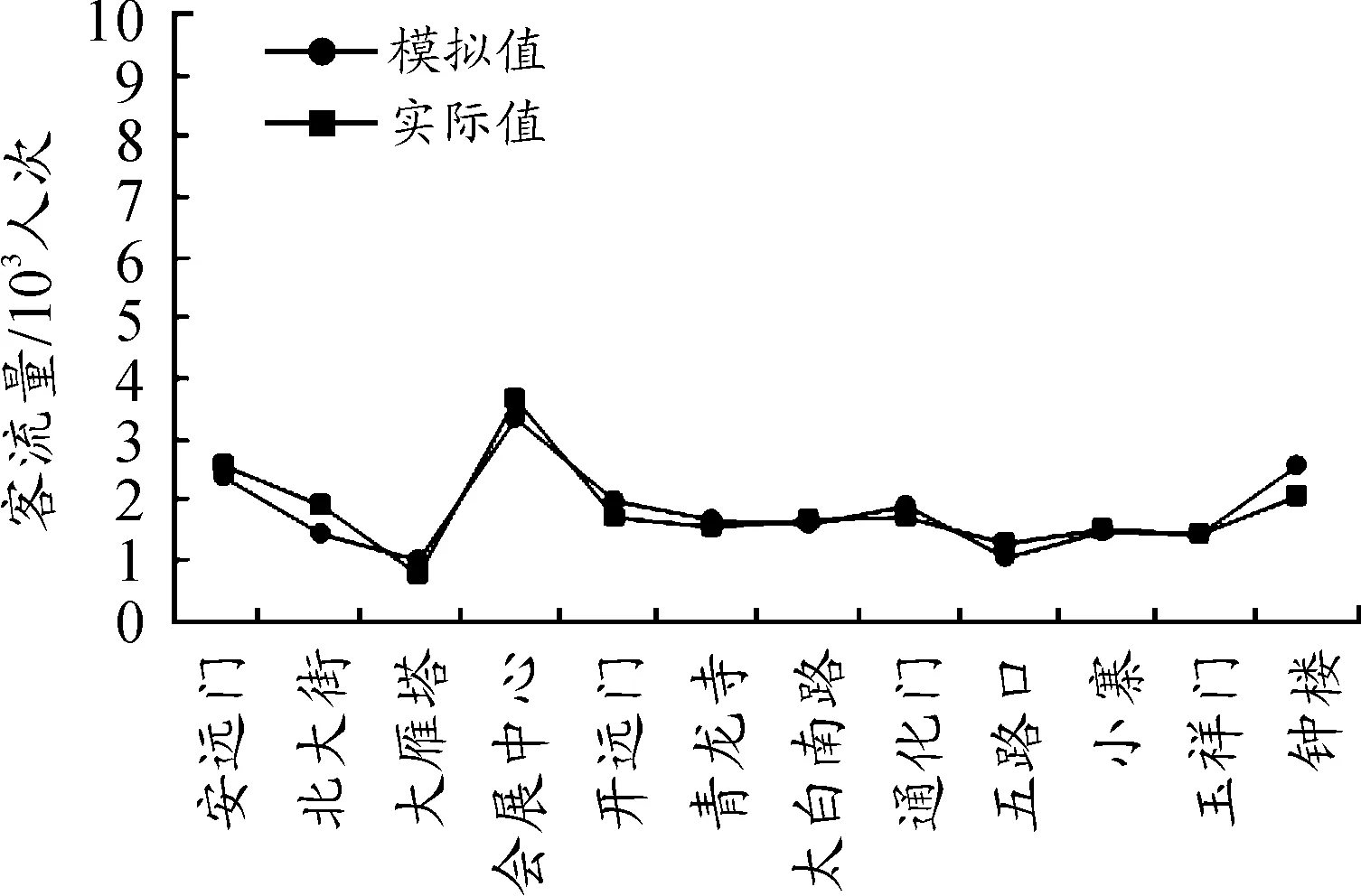
图3 早高峰进站客流量拟合结果

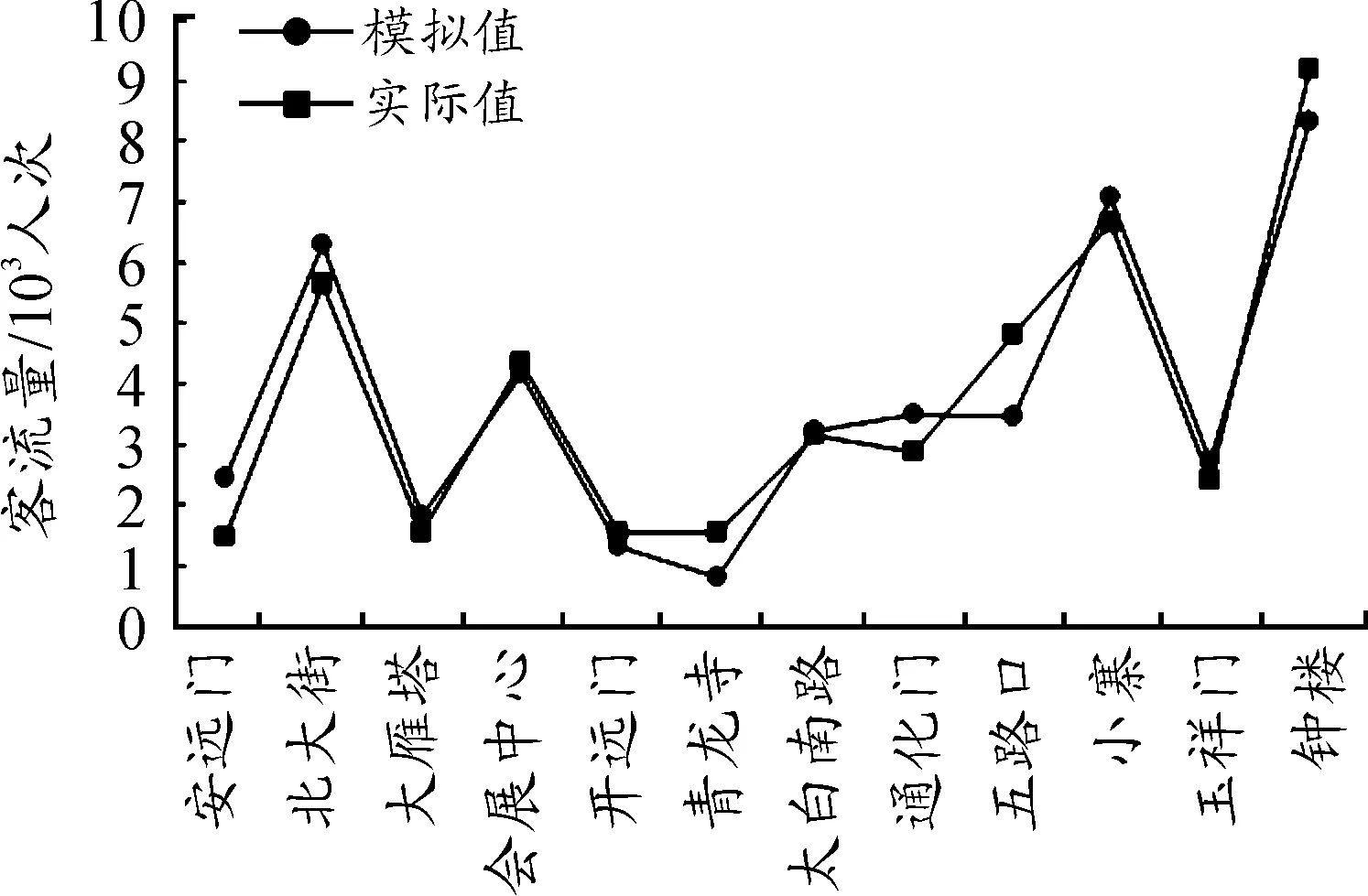
图4 早高峰出站客流量拟合结果

应用拟合模型计算西安地铁二号线的所有车站的早高峰进、出站客流量，并与实际值进行对比，如图5、6所示。模型计算结果的精度整体良好。西安北客站属于地铁和高铁衔接的枢纽站，进、出站客流量受高铁客流影响，模型计算结果误差较大。

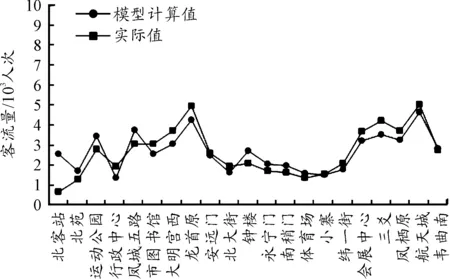
图5 早高峰进站客流量预测模型校验

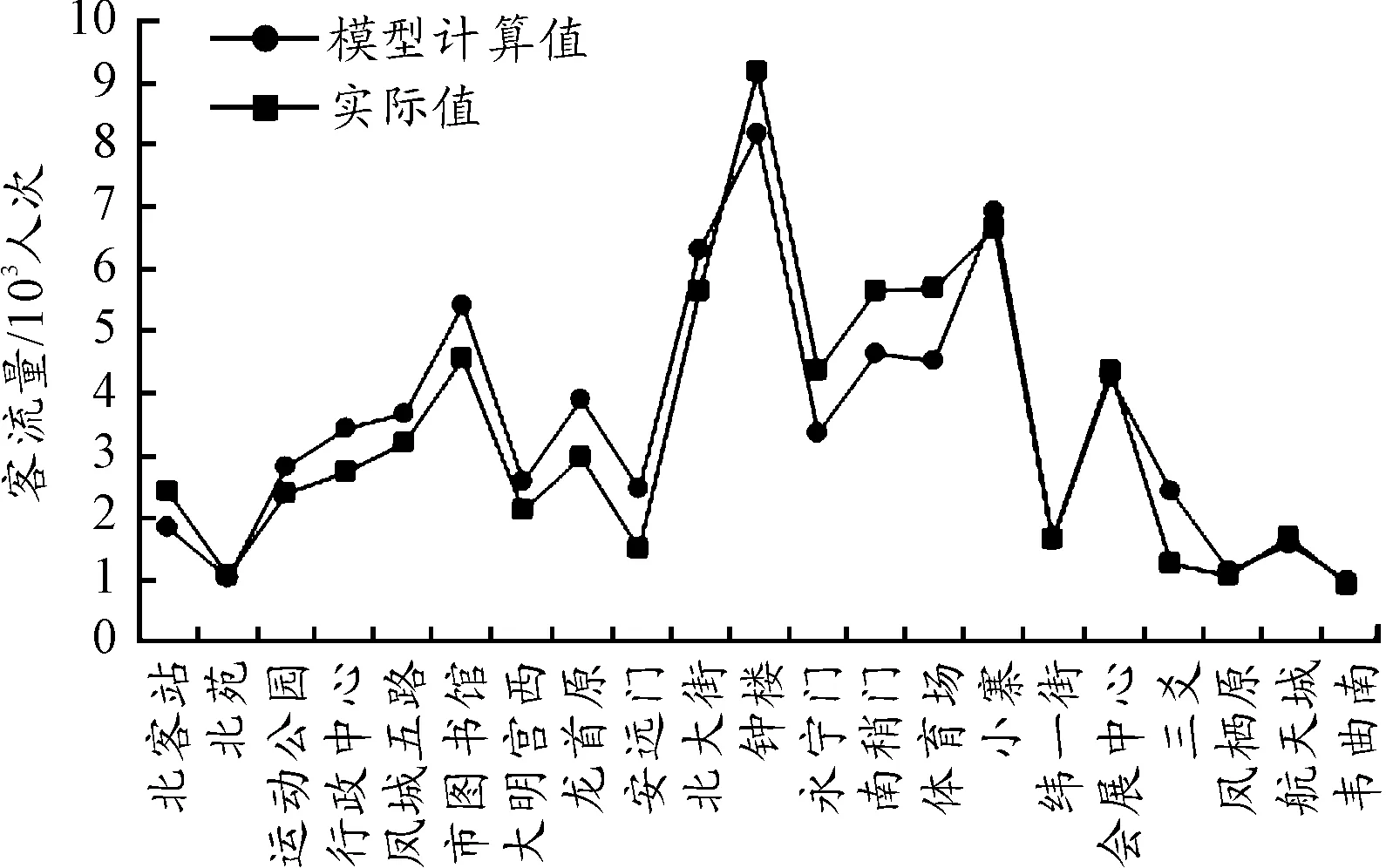
图6 早高峰出站客流量预测模型校验

3.3 晚高峰进、出站客流量

晚高峰进、出站客流量模型VIP值如表5所示。

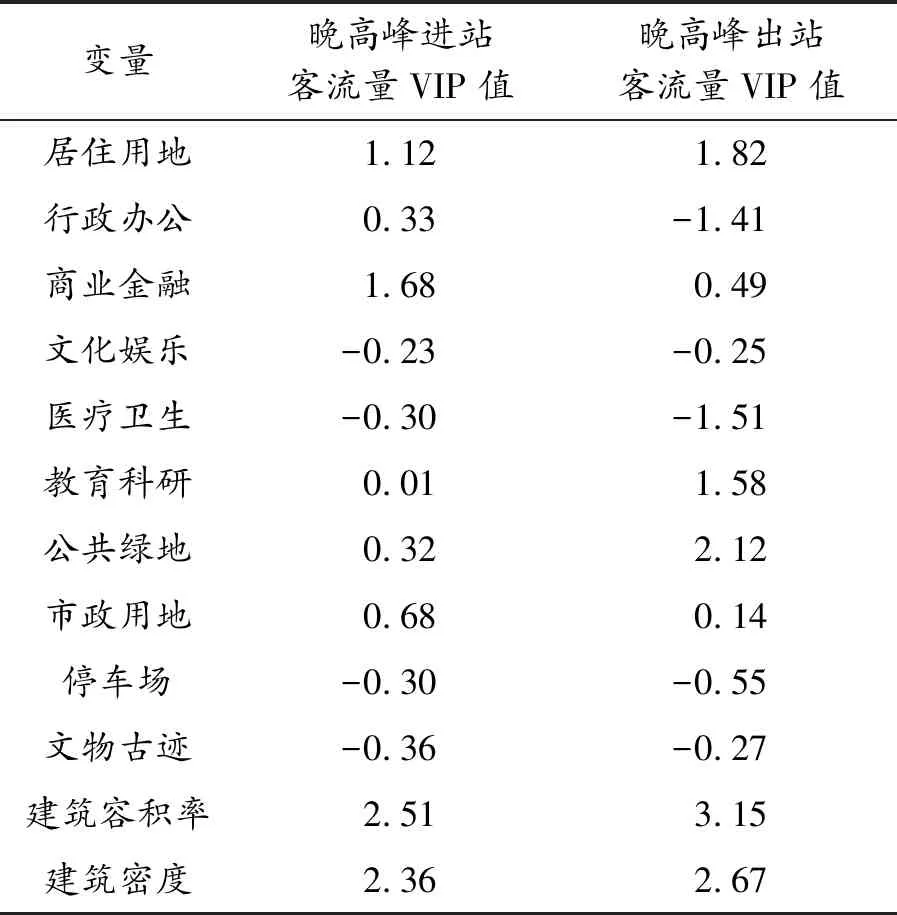
表5 晚高峰进、出站客流量VIP值

对于晚高峰进站客流量，建筑容积率、建筑密度、商业金融、居住用地的变量投影重要性指标值均超过1，说明这4个指标是构成晚高峰进站客流量的最重要影响因素。

对于晚高峰出站客流量，建筑容积率、建筑密度、公共绿地、居住用地、教育科研、医疗卫生、行政办公的变量投影重要性指标绝对值均超过1，说明这7个指标是构成晚高峰出站客流量的最重要影响因素。晚高峰出站客流量的影响因素较多，影响力较为分散。晚高峰出站客流多以下班通勤客流为主，公共绿地、居住用地多属于客流吸引源，与车站晚高峰出站客流量呈正相关；而医疗卫生、行政办公、文物古迹在晚高峰期间属于客流发生源，故与晚高峰出站客流量呈负相关。

将样本点的实测晚高峰进、出站客流量与模型拟合结果进行对比，如图7、8所示。除个别车站外，模型拟合结果与实测值基本吻合。

图7 晚高峰进站客流量拟合结果

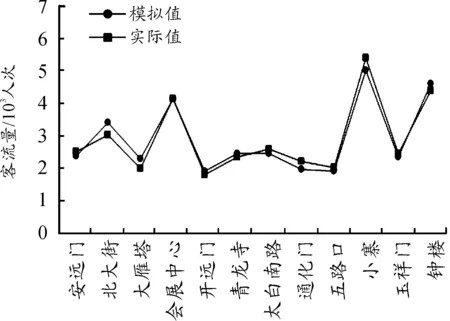
图8 晚高峰出站客流量拟合结果

应用拟合模型计算西安地铁二号线的所有车站的晚高峰进、出站客流量，并与实际值进行对比，如图9、10所示。模型拟合结果的精度整体良好。

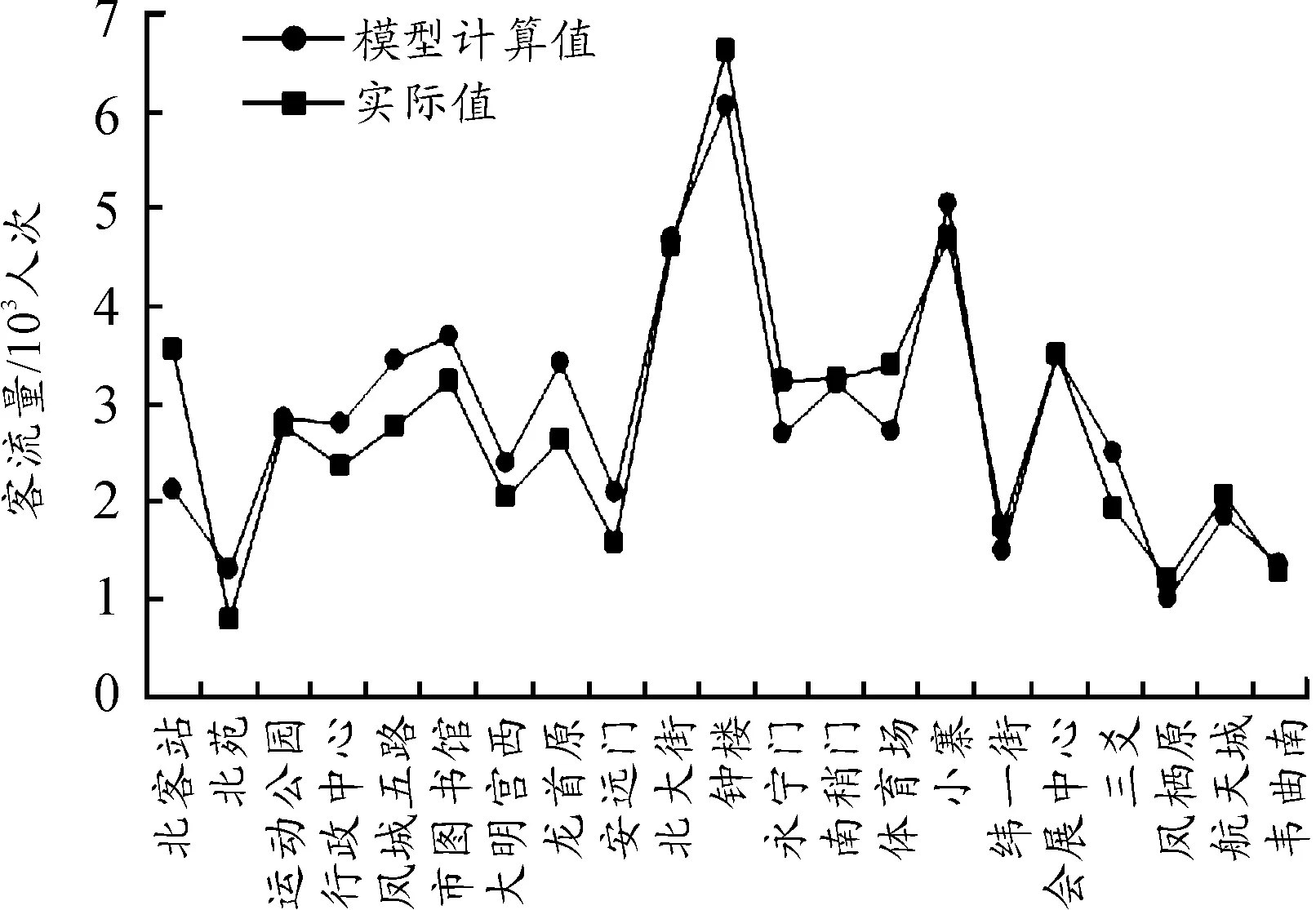
图9 晚高峰进站客流量预测模型校验

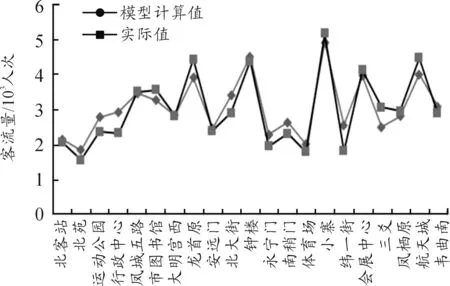
图10 晚高峰出站客流量预测模型校验

4 结论

用地类型和轨道客流之间有很强的相关性，各因素之间又存在较强的共线性。在探讨用地类型对轨道车站客流乘降量的影响时，仅依靠多元线性回归获得的模型稳健性较差，甚至得到错误的参数估计。PLSR法因采用分解和筛选数据信息的方式，提取对系统解释能力最强的成分，故能较好地克服多重共线性在系统建模中的影响，因而相对于多元线性回归和主成分分析，模型的参数估计也更加准确。

建模的结果表明：不同用地类型对轨道交通客流量有不同的影响，针对不同类型的客流，预测中必须重点把握其对应的重要指标。在一些特殊用地的车站，因变量未选取其比重较大的用地指标时，拟合精度较低。模型在选取自变量指标方面应进一步完善。在准确把握各类型规划用地的基础上，车站客流量可以通过PLSR模型进行测算估计。

随着城市轨道交通的建设，城市轨道交通的总里程迅速增长，线路之间形成网络，乘客到达目的地的可达性增加，加之其准时、快捷、方便、舒适的特点，使得城市轨道交通的客运量、客运强度大大增加。因此，能准确地预测短期进站客流变化情况，分析乘客出行特征，合理地对进站客流进行有效疏导，对车站内乘客流线的组织、列车的运营时刻表进行相应的安排，是提高乘客出行效率、舒适度，保证安全、高效地运营城市轨道交通线路的重要举措。