双场耦合破乳脱水装置的锥段结构优化

余 保,龚海峰,戴 飞

(1.重庆理工大学 机械工程学院， 重庆 400054； 2.重庆工商大学 废油资源化技术与装备教育部工程研究中心， 重庆 400067)

工业废油的资源化再利用对于缓解能源紧缺、节约资源以及环境保护等具有重要意义[1-3]。乳化液的破乳脱水处理是众多资源化再利用工艺中的首要环节[4]。对于含水量较高、成分复杂的废油乳化液，各种单一的工艺方法在处理成本、耗能及耗时等方面均存在局限，采用多场耦合或集成技术实现乳化液高效破乳脱水处理是未来发展的趋势[5]。因此，提出了一种集成高压电场和旋流离心场的耦合破乳脱水装置[6]。该装置以双锥脱水型旋流器为本体结构嵌入高压电极。在不同的应用目的、需求以及进给材料参数下，对本体结构的结构参数进行优化可有效地提高装置的分离效率[7]。响应面法作为一种以数学统计为基础的非线性优化方法，可用于分离装置的多个结构参数优化[8-10]。Tang 等[11]利用中心组合设计和响应面法对旋流器溢流口结构参数进行了优化，且发现经过优化后的装置具有更高的分离精度。Vieira等[12]利用数值计算以及响应面法对旋流器的几何参数进行了优化，结果表明：经几何参数优化后的装置具有较低的欧拉数和更小的截断尺寸。

由于耦合装置本体结构的锥形段是非常重要的分离区域，通过优化锥形段的结构参数可以有效地改善耦合装置的分离效率。因此，尝试利用响应面法对耦合装置的锥段结构进行优化。采用数值模拟方法，结合Box-Behnken因子设计和响应面法对耦合装置的几何参数进行优化，对设计和制造高性能的双场耦合破乳脱水装置具有指导意义。

1 模型与方法

1.1 模型与方程

双场耦合破乳脱水装置的结构模型如图1所示。该模型主要包括直管段、大锥段、小锥段和底流管。在直管段包括一个溢流管和2个圆柱形入口，且2个圆柱形入口与直管段相切。溢流管的柱形外壁为电源的正极，直管段的柱形内壁为高压电源的负极，在两柱形壁面之间区域内形成高压电场。乳化液经入口进入到该区域内，乳化液中的分散相液滴在高压电场作用下发生快速聚结使其粒径变大，然后在旋流作用下快速地分离。建立以底流口中心点为原点的笛卡尔坐标系，z轴沿中轴线并指向溢流口。耦合脱水装置的主要结构参数主要包括公称直径D、直管段直径DS、溢流口直径DO、入口直径Di、溢流管伸入长度Lo、底流管长度Lu、底流口直径Du、小锥角α和大锥角β。在本研究中，DS、DO、Di、Lo、Lu、Du的值分别为70 mm、18 mm、12 mm、45 mm、400 mm和10 mm，且均保持不变。

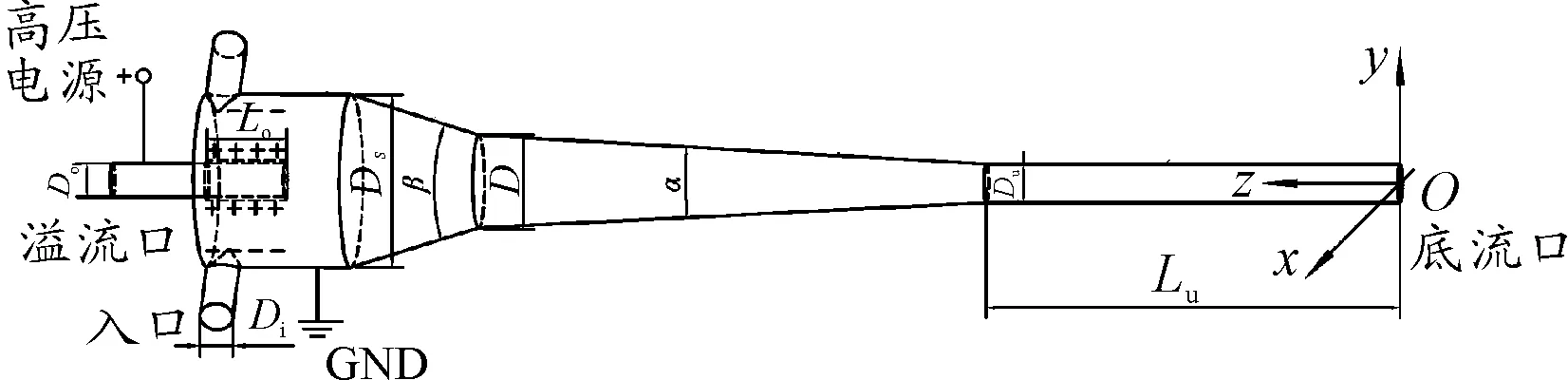
图1 双场耦合装置结构模型

耦合装置内部为复杂的湍流流动，且满足不可压缩流的运动条件。控制方程采用Mixture模型，用雷诺应力模型对湍流流动情况进行模拟。Mixture模型和雷诺应力模型的具体表达见文献[13]。

由于高压电场的存在，在耦合装置中的分散相液滴会受到电场力。电场力可由式(1)表达。

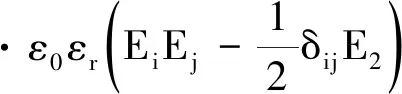
(1)

式中：ε0为真空绝对介电常数(F/m)；εr为相对介电常数；Ei，i=1,2,3表示沿着x、y、z方向电场强度(kV/m)；Ej，j=1,2,3表示沿着x、y、z方向电场强度(kV/m)；δij为克罗内克符号；E为电场幅值有效值(kV/m)。

在高压电场区域，分散相液滴发生聚结后粒径发生变化。根据液滴聚结模型[14]，粒径控制方程可表达为 ：

(2)

n=[t/t1]

(3)

R′=(2n)1/3R

(4)

式(2)～(4)中：t1为液滴成对结聚时间(s)；μ为油液动力黏度(Pa·s)；φw为油中含水体积分数(%)；n为[t/t1]的整数部分；t为液滴在电场区停留时间(s)；R为聚结前液滴半径(mm)；R′为聚结后液滴半径(mm)。

1.2 网格划分与边界条件

利用ANSYS Meshing(ANSYS 15.0)对耦合装置模型进行网格划分。采用自动划分的方式进行非结构网格划分。为确定网格的独立性，初始网格数量为248 967，在相同边界条件下，将网格数量增大到342 128，计算后得到直管段内最大切向速度的改变量超过5%，再增大网格数量到422 987时，最大切向速度值的改变量不超过5%。因此，考虑到预测精度以及计算花费，网格数量为342 128可以满足数值计算要求。

设圆柱形入口为速度入口，且其法向速度为10 m/s，轴向和径向速度为0。入口处的湍流强度为5%，水力直径为12 mm。设耦合模型的溢流口和底流口为自由出流，且分流比分别为0.9和0.1。其他壁面为无滑移边界条件。在靠近壁面区域采用标准壁面函数。高压电场电压幅值为11 kV。

1.3 物性参数与求解器设置

乳化液中连续相为油，分散相为水。油的含水量为10%，其分散相水滴平均粒径为200 μm。为了确保乳化液在耦合装置中能有较好的分离效果，对油液进行加热，温度设定为70 ℃。在该温度下，油相的密度为863 kg/m3，黏度为16.807 mPa·s；水相的密度为998.3 kg/m3，黏度为1.3 mPa·s。

采用CFD软件ANSYS Fluent(ANSYS 15.0)对不同结构参数下的耦合装置数值模型进行计算。将用户自定义函数方法用于定义高压电场方程以及粒径控制方程，以实现电场与流场的耦合模拟计算[15]。采用有限体积法对三维、不可压缩流动的Navier-Stokes方程进行离散。semi-implicit method for pressure linked equations consistent(SIMPLE)代码用于耦合连续性方程以及动量方程中的压力与速度求解。quadratic upstream interpolation for convective kinetics(QUICK)格式用于动量方程、体积分数方程、雷诺应力方程、湍动能以及湍流耗散率方程的离散。PREssure staggered option (PRESTO)格式用于压力插值。所有的数值模型均采用瞬态模拟，且时间步长为0.05 s。

2 结果与分析

2.1 参数设计及计算结果

设大锥角、小锥角和公称直径的取值范围分别为：20° ～ 22°、5° ～ 6°和20 ～22 mm。利用Box-Behnken试验设计原理，对3个因素(大锥角、小锥角和公称直径)及其水平进行响应面设计，优化耦合脱水装置锥段尺寸。以装置溢流口脱水率和底流口脱油率为响应值，自变量为小锥角(°)、大锥角(°)和公称直径(mm)。各因子编码及自变量水平如表1所示。利用Design-Expert 软件按表1中的因子编码及自变量水平进行试验设计，同时利用数值方法得出各试验条件下的响应值，其结果如表2所示。

表1 试验因子水平及编码

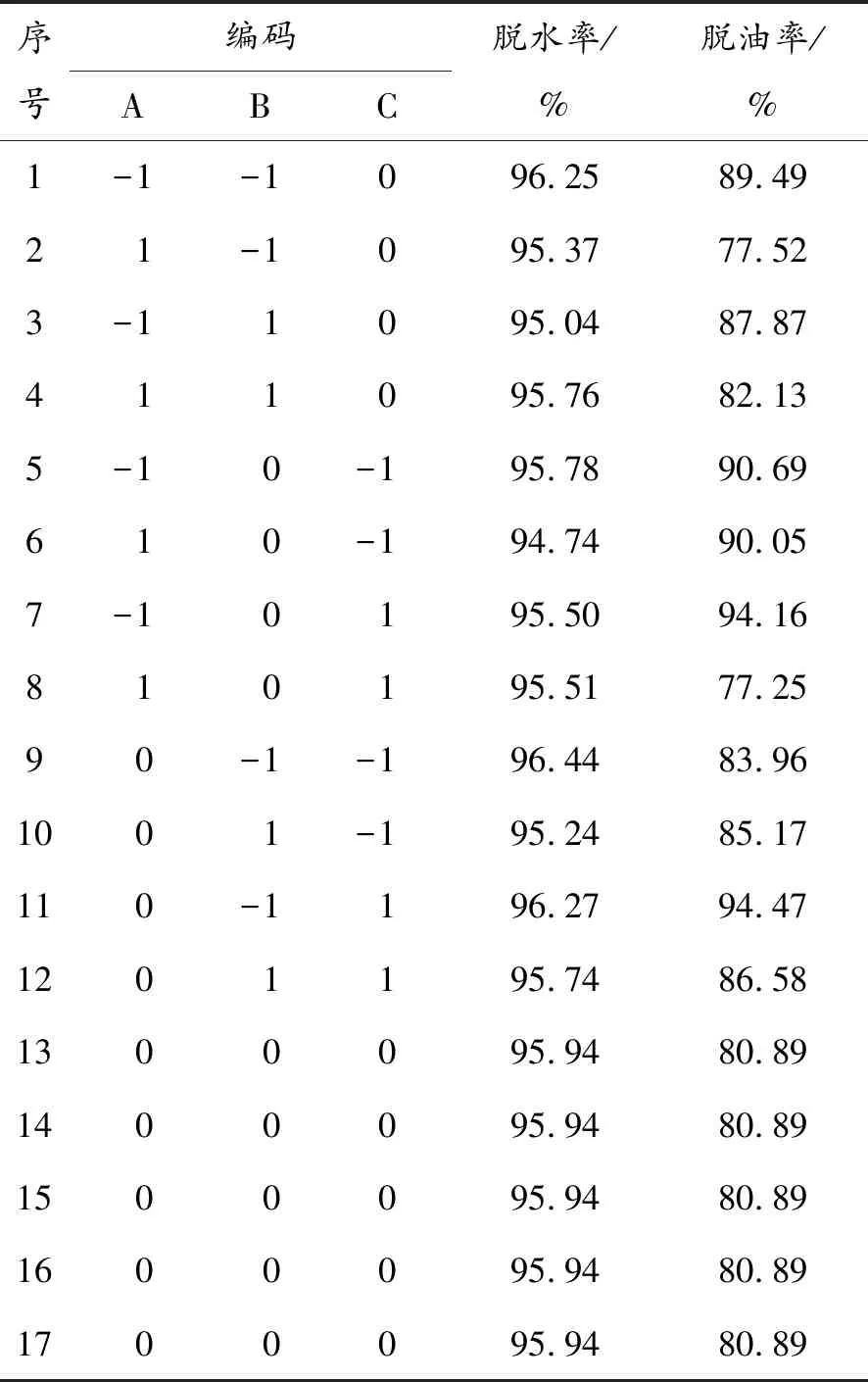
表2 Box-Behnken试验设计方案及结果

2.2 响应模型与方差分析

采用Design-Expert 8.0软件对表2中的数据进行响应面分析，建立多元二次回归模型：

Edw=266.26-8.798x1-12.43x2-1.197x3+

0.799x1x2+0.528x1x3+0.166x2x3-

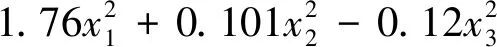
(5)

Edo=1716.68+11.68x1-29.9x2-126.5x3+

3.11x1x2-8.13x1x3-2.28x2x3+

(6)

式中：x1、x2和x3分别对应α、β和D；Edw为脱水率(%)；Edo为脱油率(%)。

二次回归模型的方差分析结果如表3和表4所示。从表3、4中可以看出：模型的F-value分别为11.74和4.61，与其对应的p-value分别为0.19%和2.81%，均小于5%，即式(5)和式(6)表示的响应模型是显著的。其中，脱水率响应模型中的显著项有A、B、AB、AC和A2；脱油率响应模型中的显著项有A、AC和C2。此外，两响应模型的复相关系数值R2分别为0.937 9和0.855 7，表明模型均具有较高的显著性。

表3 脱水率的模型方差分析结果

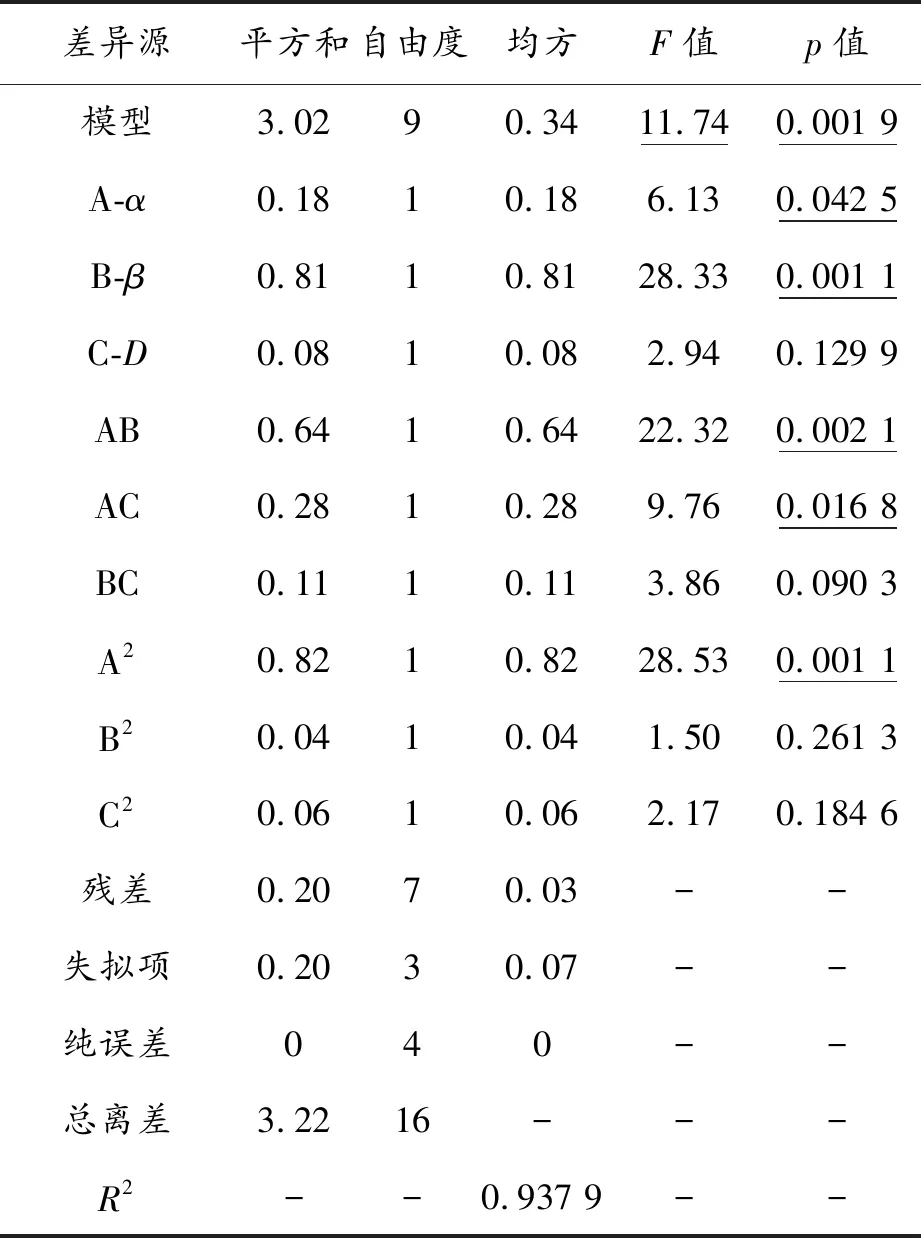
差异源平方和自由度均方F值p值模型3.0290.3411.740.001 9A-α0.1810.186.130.042 5B-β0.8110.8128.330.001 1C-D0.0810.082.940.129 9AB0.6410.6422.320.002 1AC0.2810.289.760.016 8BC0.1110.113.860.090 3A20.8210.8228.530.001 1B20.0410.041.500.261 3C20.0610.062.170.184 6残差0.2070.03--失拟项0.2030.07--纯误差040--总离差3.2216---R2--0.937 9--

耦合脱水装置脱水率和脱油率的可信度分析结果如图2所示。从图2可以看出：预测值与实际值接近，表明响应模型与数值计算拟合度较好。

为进一步研究各因素间的交互作用对分离效率的影响，本文对二次回归模型进行响应面分析，得到的响应立体分析结果和等高线图如图3、4所示。从图3中可以看出：同时减少小锥角α和大锥角β可较小程度地提高装置溢流口脱水率，且当小锥角为5°时，大锥角从22°减小到20°，脱水率从95.03%增大到96.24%。图4中可见：同时增大公称直径D和减少小锥角α可以明显地提高底流口脱油率，且当小锥角为5°时，公称直径D从20 mm增大到22 mm，脱油率从90.69%增大到94.16%。

表4 脱油率的模型方差分析结果

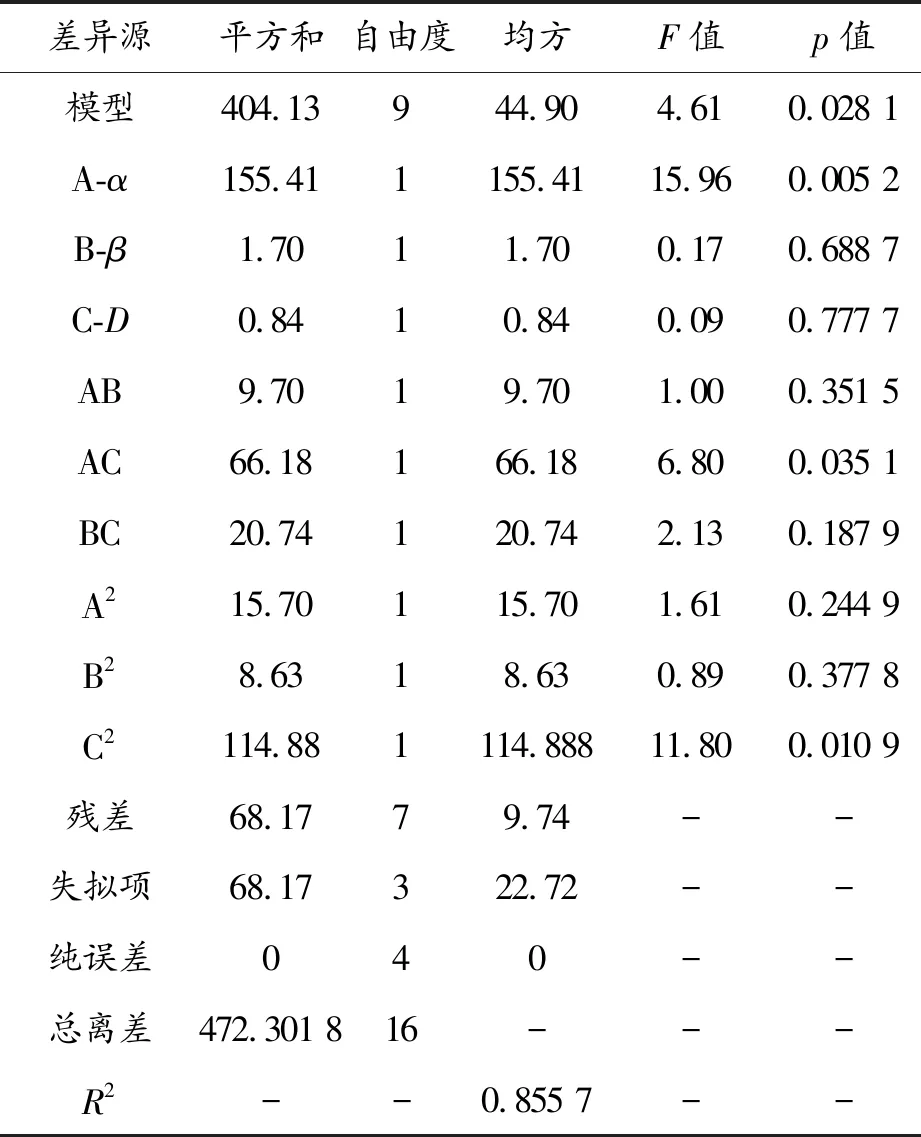
差异源平方和自由度均方F值p值模型404.13944.904.610.028 1A-α155.411155.4115.960.005 2B-β1.7011.700.170.688 7C-D0.8410.840.090.777 7AB9.7019.701.000.351 5AC66.18166.186.800.035 1BC20.74120.742.130.187 9A215.70115.701.610.244 9B28.6318.630.890.377 8C2114.881114.88811.800.010 9残差68.1779.74--失拟项68.17322.72--纯误差040--总离差472.301 816---R2--0.855 7--

2.3 最佳结构参数

以装置的脱水率和脱油率达到最大值为最优条件，通过对响应模型进行求解分析得到优化结果；同时，为验证响应曲面模型求解的合理性，在最佳分离效率条件下采用数值计算方法对装置模型进行模拟计算，得到的结果如表5所示。表5中：S表示模拟计算值；P表示模型预测值。由表5可知：响应模型的预测值与数值计算值相差较小，其中：脱水率响应模型的最大偏差约为0.24%，脱油率响应模型的最大偏差为3.46%。因此，响应模型的最优解是合理的。

表5 优化条件下模拟值与预测值

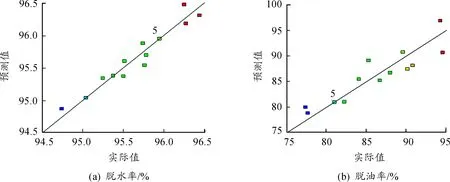
图2 预期值与实际值对比曲线

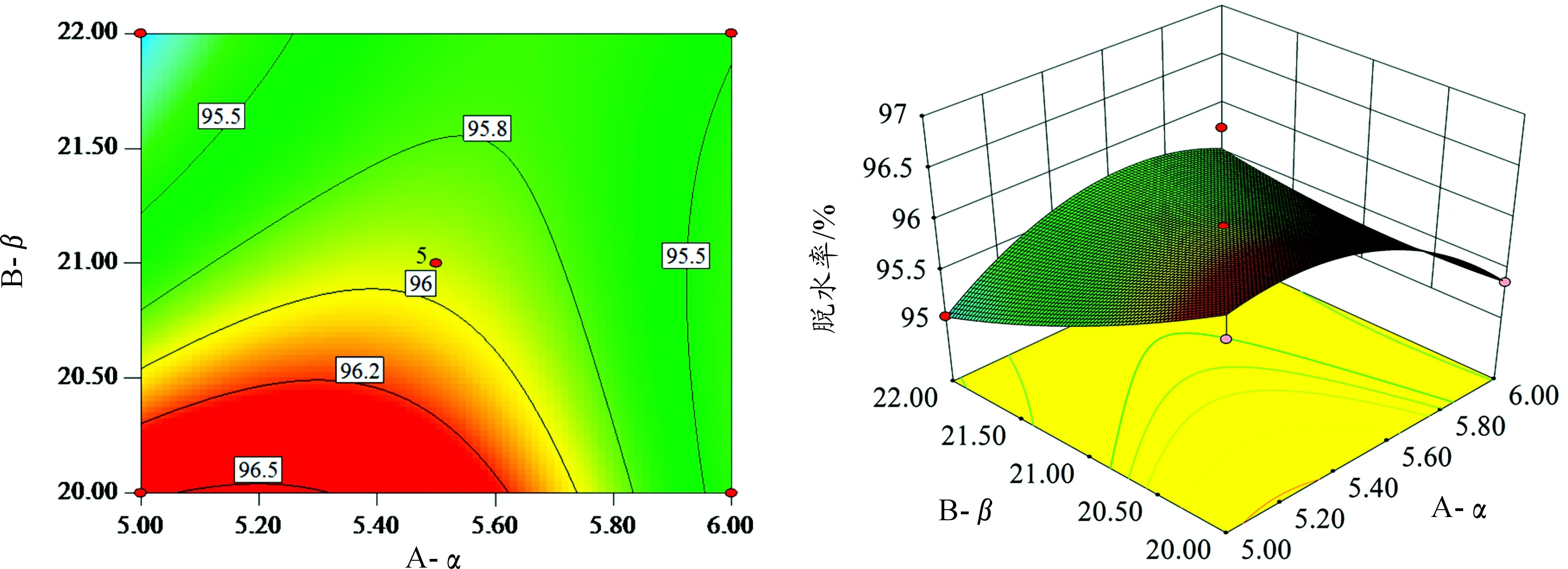
图3 α-β间的交互作用对脱水率的影响

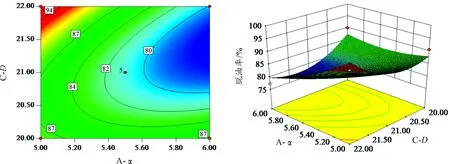
图4 α-D间的交互作用对脱油率的影响

3 结论

针对双场耦合破乳脱水装置用Design Expert 8.0软件建立响应模型对其锥段结构进行优化。

1) 利用数值模拟，结合使用Box-Behnken因子设计和响应面法，建立了各结构参数与分离效率间的拟合回归模型。小锥角与大锥角之间的交互作用对装置溢流口脱水率的影响显著；小锥角与公称直径之间的交互作用对装置底流口脱油率的影响显著。

2) 根据响应模型计算结果，得到最佳结构参数为：小锥角、大锥角和公称直径的最佳取值分别为5.09°、20°和22 mm，且在该条件下耦合装置的脱水率和脱油率的数值计算值分别为96.46%和97.05%。