基于小波变换的伺服电机位置检测误差修正方法

彭东林，唐渐鸿，王淑娴，张 准

(重庆理工大学 机械检测技术与装备教育部工程研究中心 时栅传感及先进检测技术重庆市重点实验室, 重庆 400054)

随着对复杂机电系统智能化研究的不断深入，获取准确的电机位置信息日益重要。时栅课题组利用隧穿磁电阻(TMR)体积小、灵敏度高、易集成化、成本低的特点[1]，直接将检测元件TMR芯片嵌入永磁伺服电机内部来检测电机转动过程中位于转子上的多对极永磁体产生的旋转磁场变化，并结合时栅技术来实现永磁伺服电机嵌入式位置检测，测量精度达到±1.8°[2-3]。这是由于在检测过程中不可避免地存在因机械加工和机械安装引入的误差，降低了测量精度。在精密检测理论中误差修正技术是提高测量精度最常用的有效方法[4-6]。

根据近年来国内外的研究学者对误差修正方法的大量研究，目前常用修正方法可归纳为以下几种：最小二乘法曲线拟合[7]、傅氏级数谐波修正法[8-10]、短时傅里叶变换[11-13]。最小二乘法以实验数据与拟合值差值的平方和最小为理想结果，但不适合高精度的拟合[14]。傅氏级数谐波修正法实现了信号从时域到频域的转换，然而它只能得到整段信号中存在的频率成分，却无法判断各频率成分出现的时刻。短时傅里叶变换通过窗口函数分割信号，信号在分割后的时间段内进行傅里叶变换，获得相应时段的频域信息，但是短时傅里叶变换的时域分辨力取决于不可调形状和大小的时间窗[15]。小波的多分辨率分析的特性克服了短时傅里叶变换的缺陷，根据信号的具体形态动态调整时间窗和频率窗，实现了更精准的时域定位。因此，将小波应用在动态检测中可以更好地聚焦误差数据的细节，很好地补偿与位置相关的误差。

基于上述分析，本文提出基于小波变换的伺服电机嵌入式位置检测误差修正方法，构建了相关算法程序流程，搭建了伺服电机嵌入式位置动态检测实验系统，借助Matlab软件对此修正方法进行测试，有效地提高了伺服电机嵌入式位置检测精度。

1 伺服电机嵌入式位置检测误差修正原理

1.1 伺服电机嵌入式位置动态检测系统

如图1(a)所示，一对空间正交放置(相距90°电角度)的TMR芯片嵌入在电机端盖中用于感应电机内部旋转磁场的变化。随着电机的转动，气隙磁场为正、余弦变化，同时给一对TMR芯片分别加载时间正交(90°相位差)的正、余弦激励，则这一对TMR芯片输出相位相差90°的驻波信号，两路驻波信号叠加后得到携带电机转子位置信息的行波信号，将行波信号送入时栅信号处理系统，通过信号处理、角位移计算后得到电机的转动位置，实现了永磁伺服电机嵌入式位置检测。永磁伺服电机嵌入式位置检测内部结构如图1(b)所示。

然而在伺服电机位置的实际检测中，存在几种误差源降低了测量精度[2]。电机轴与TMR芯片安装轴不同心会导致TMR在整周内感应的磁场不均匀变化，引入整周内长周期一次谐波误差。2个TMR芯片安装不在同一圆水平面会导致四路差分信号的幅值不一致，引入短周期一、二次谐波误差。2个TMR芯片的个体差异、空间位置上不正交、两路激励信号时间上不正交、幅值不相等会导致两路驻波幅值不相等，引入短周期二次谐波误差。电磁干扰及其他因素会为测量结果引入高次谐波误差。

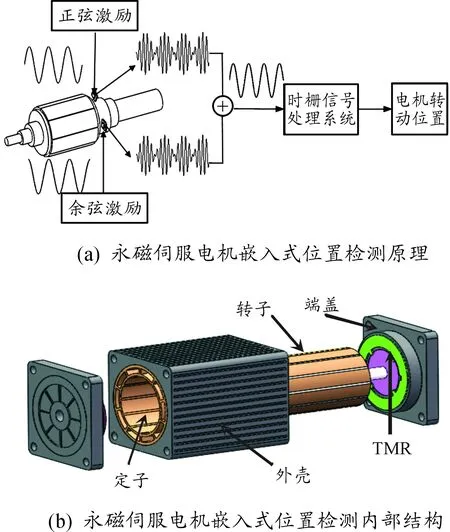
图1 永磁伺服电机嵌入式位置检测原理及其内部结构

为了补偿误差提高测量精度，设计了图2所示的伺服电机位置动态检测系统。嵌入在电机端盖中的TMR芯片感应变化的磁场输出携带转子信息的时栅信号。光电编码器作为基准量仪通过连接装置与电机轴同心连接，得到基准信号。下位机由FPGA和DSP组成，实现对信号进行数字化处理和计算，输送测量数据到上位机。上位机对误差数据进行分析、处理及显示。首先，对低转速下的误差数据进行小波分解，得到此转速下误差数据的小波分解近似及细节系数序列、小波基函数对应低通和高通滤波器系数，并将所有系数储存。然后，在标定过程中转换实时转速下插值点的坐标值到低转速下对应的坐标值，通过选择插值数值周围的系列相邻系数对小波系数进行线性插值，进而得到插值点的近似以及细节系数。最后，对插值后的近似及细节系数序列与低、高通滤波器系数进行卷积运算实现数据重构，从而得到实时转速下插值点的测角误差值，最终输出实时转速下角位移测量值。

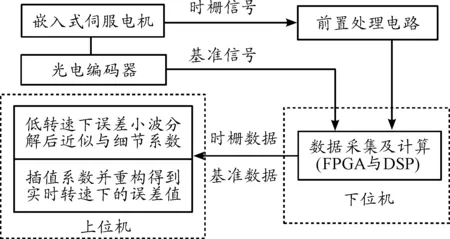
图2 伺服电机嵌入式位置动态检测系统框图

1.2 小波变换的思想

在图3中直观地表示了小波与正弦波的区别。正弦波是一个在无限区域幅值恒定的周期性函数，小波是一个在有限区域内存在且幅值衰减的函数，小波数学描述为：

(1)

(2)

(3)

式中：ε取0<ε<1的任何一个数。

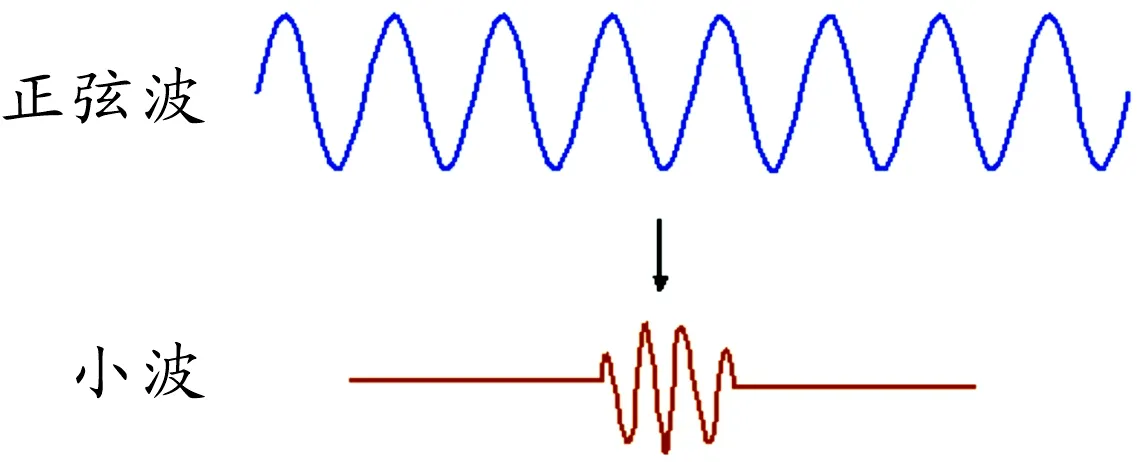
图3 小波与正弦波的比较

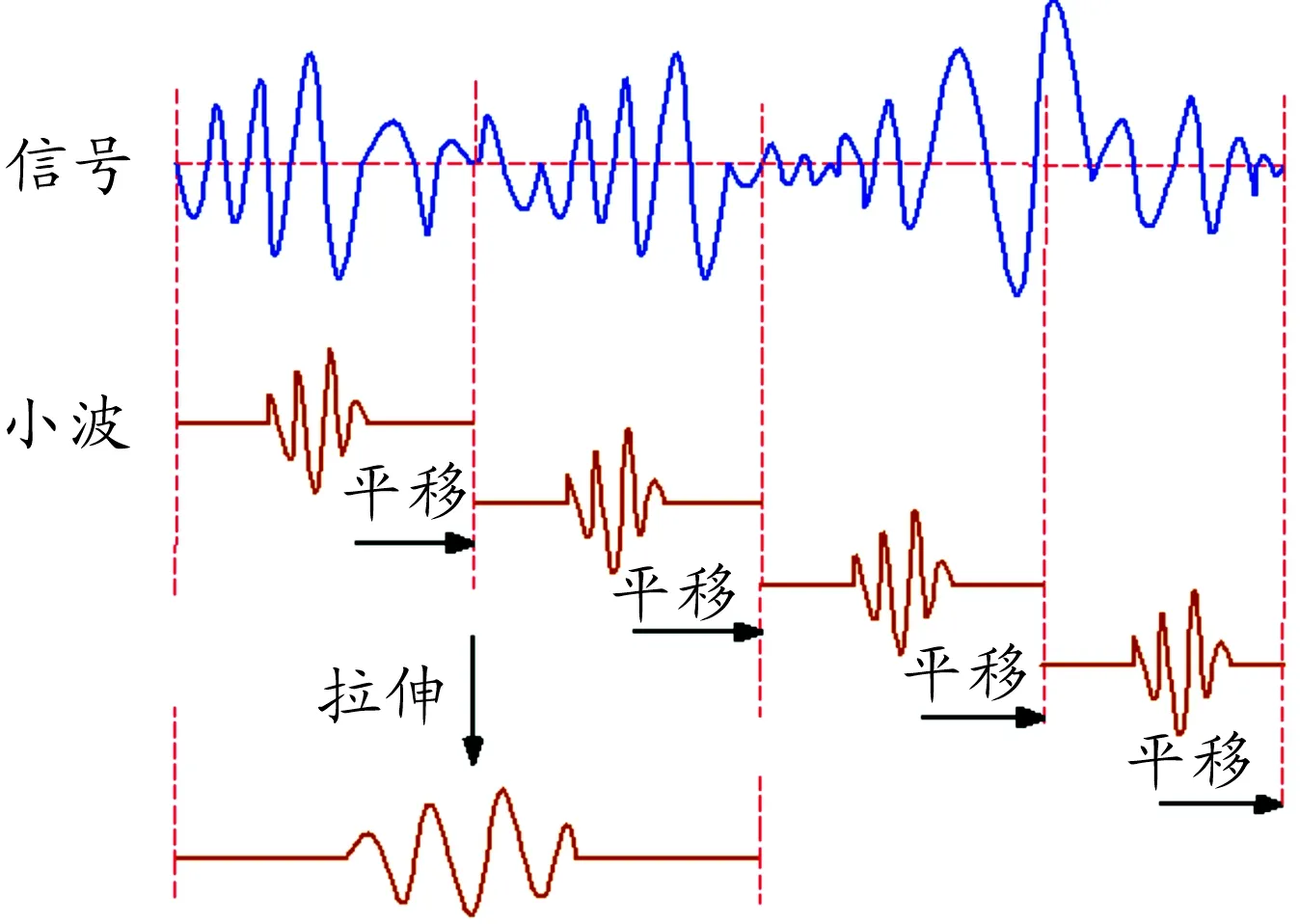
图4 小波变换实质

小波分析是一种变分辨率的时频分析方法，在时域和频域都具有很好的表现信号局部信息的能力[16-17]。如图4所示，小波变换的实质是信号与小波函数的卷积，利用不同尺度的小波对不同时刻的信号进行卷积运算，得到的一序列的系数反映了不同尺度的小波函数与不同时刻的信号的近似程度，从而得到信号在各个时刻上的频率成分。

在多分辨率特性的基础上，小波级数的展开式表达为：

(5)

式中：dk,n=〈f,ψk,n(u)〉为小波系数或细节系数；k为尺度因子；n为平移因子。

dk,n体现的是变换后信号的高频部分，k和n都在-∞到+∞之间取值，即在所有不同的尺度上作细化处理，然而当细化尺度超过一定的特定尺度或分辨率(如m0)之后，细节特征就失去了作用。因此，以m0为界限，m0以下各尺度用于基本特征的提取，m0以上作细化特征近似，可得到新的小波级数展开式：

(6)

式中：dk,n=〈f,ψk,n(u)〉 为细节系数；cm0,n=〈f,ψm0,n(u)〉为近似系数。

在小波变换中小波基函数的选取十分重要。选择的小波母函数不同，经过小波分解，插值小波系数后重构得到的信号值也不同，所以小波母函数的选取需依据以下几点：① 小波的支撑长度要适中，过大会增加计算量，过小则会损失信号的细节。② 消失矩阶数需折中选择，越高信号越平滑，但是其支撑长度过长。③ 选择具有对称性的小波，能够较准确地还原出原始信号。④ 选择正则性好的小波，能在小波重构中获得较好的平滑效果。

1.3 伺服电机嵌入式位置检测中基于小波变换的插值算法的实现

小波变换在伺服电机嵌入式位置检测中的应用步骤如下：

1) 选取合适的小波基函数及分解的层数，从导入的低转速下得到的误差数据中反算出细节系数dk,n和近似系数cm0,n。

2) 对分解后的系数进行插值处理。

3) 重构实时转速下插值点的误差值。

依据小波基函数的选取准则，本文选取具有较高的正则性以及具有高度对称性的“sym5”作为小波基函数，其支撑长度为9，滤波器长度为10，消失矩阶数为5。

选取小波基函数后，执行如图5所示的程序算法。首先获得伺服电机在低转速nr/min下相对标准量仪的测角误差数据x，运用命令“[L,H]=dwt(x,′sym5′)”对x进行单层小波分解，得到此转速下误差数据的近似系数序列L和细节系数序列H，利用“[Lo_R,Hi_R]=wfilters(‘sym5’,‘r’)”得到由小波“sym5”产生的低通和高通滤波器系数，并将所有系数存储。标定时，将实时转速m下插值点的横坐标p转换到低转速n下对应的横坐标值pi，由线性插值得到插值点的近似系数y1和细节系数y2，对线性插值后的系数序列进行二元插值，运用“x1=conv2(chazhi1,Lo_R,‘full’)”与“x2=conv2(chazhi2,Hi_R,‘full’)”对二元插值后近似及细节系数序列与低、高通滤波器系数序列进行卷积运算实现数据重构，得到实时转速下插值点的测角误差值x′。最后，测量值减去基于小波变换的线性插值算法得到的测量误差值，输出最终的实时转速下角位移测量值。

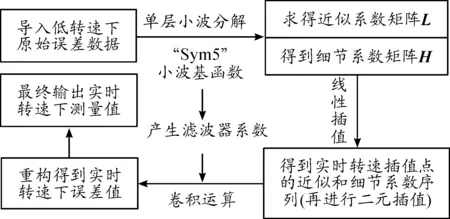
图5 程序流程

2 实验验证及分析

2.1 实验平台的搭建

为了验证本文提出的误差修正技术的可行性，搭建了如图6所示的实验系统。系统包括直流电源、嵌入TMR芯片的永磁伺服电机、下位机(信号处理板)、光电编码器(型号ZKT-58A，精度±1′)、预处理电路、上位机等装置。以额定功率为750 W的8极9槽面装式永磁伺服电机为测量对象，通过比较时栅信号和基准信号对同一角位移的动态测量值得到原始误差。借助Matlab软件对基于小波变换的伺服电机位置检测误差修正方法进行测试。

图6 实验平台

2.2 实验结果及分析

本文实验采用4对极的永磁伺服电机，单对极对应的角度为90°。永磁伺服电机在120 r/min转速下，原始误差曲线及谐波成分如图7所示。由图7(a)可以看出，整周内原始误差的峰值为1.8°，一次谐波误差比较突出，正是电机轴与TMR芯片安装轴不同心引入长周期一次谐波误差。

如图7(b)所示，在单对极内对误差曲线进行谐波成分分析，可以看出在短周期内，以一、二、四次谐波误差为主，且一次谐波误差最大。与前文误差分析一致：验证了正是2个TMR芯片安装不在同一水平面引入短周期一、二次谐波误差；2个TMR芯片的个体差异、空间位置上不正交、激励信号时间上不正交、幅值不相等引入了短周期二次谐波误差。

根据前文程序流程图，首先测得交流永磁伺服电机在低转速1 r/min下的误差数据，经过用基于小波变换的插值算法对永磁伺服电机嵌入式位置检测误差进行修正，重构得到120 r/min转速下的误差曲线如图8所示，可以看出由电机轴与TMR芯片安装轴不同心引入的长周期一次谐波误差明显降低，修正后误差达到±30′，精度提高约3.6倍。

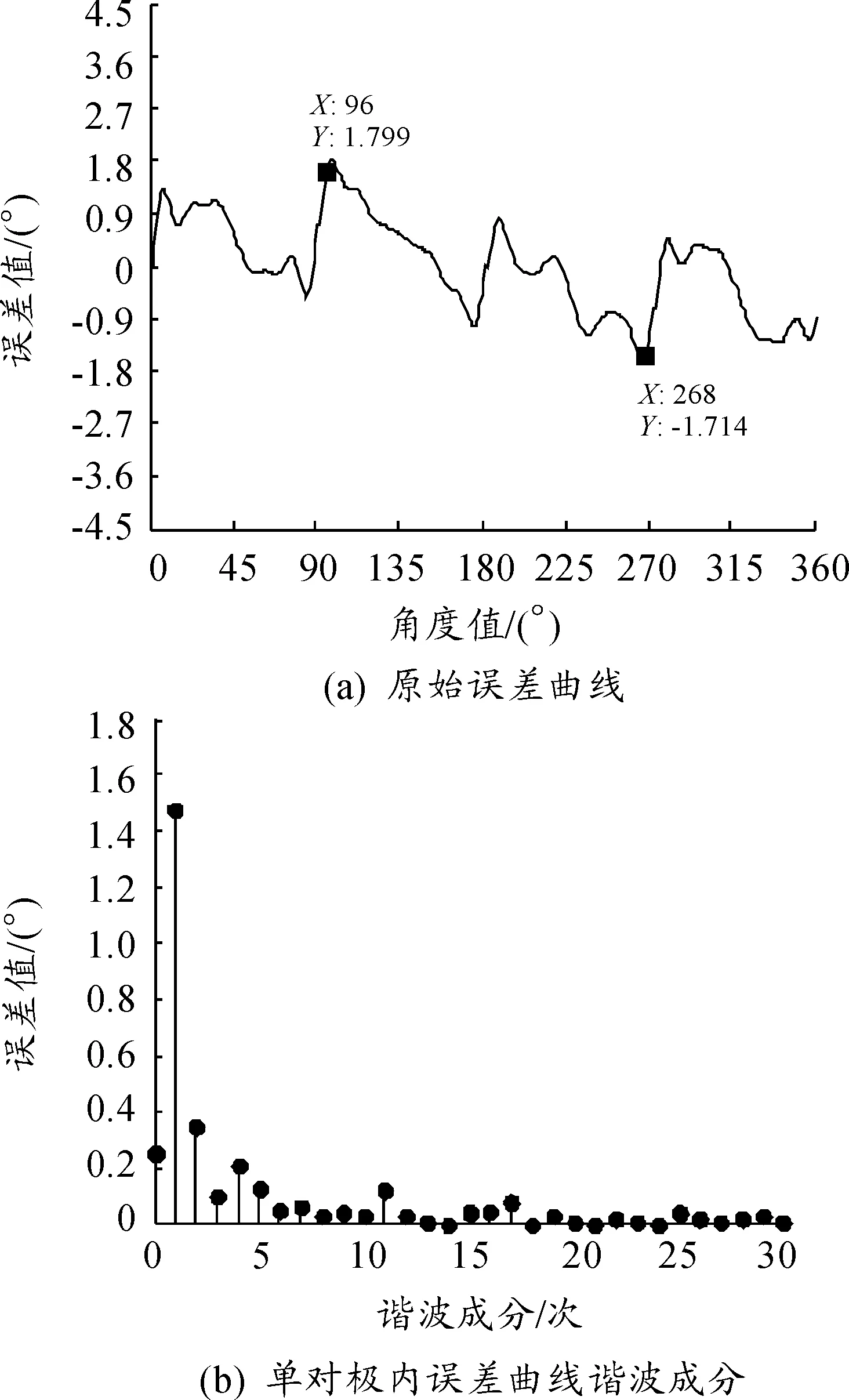
图7 原始误差曲线及谐波成分

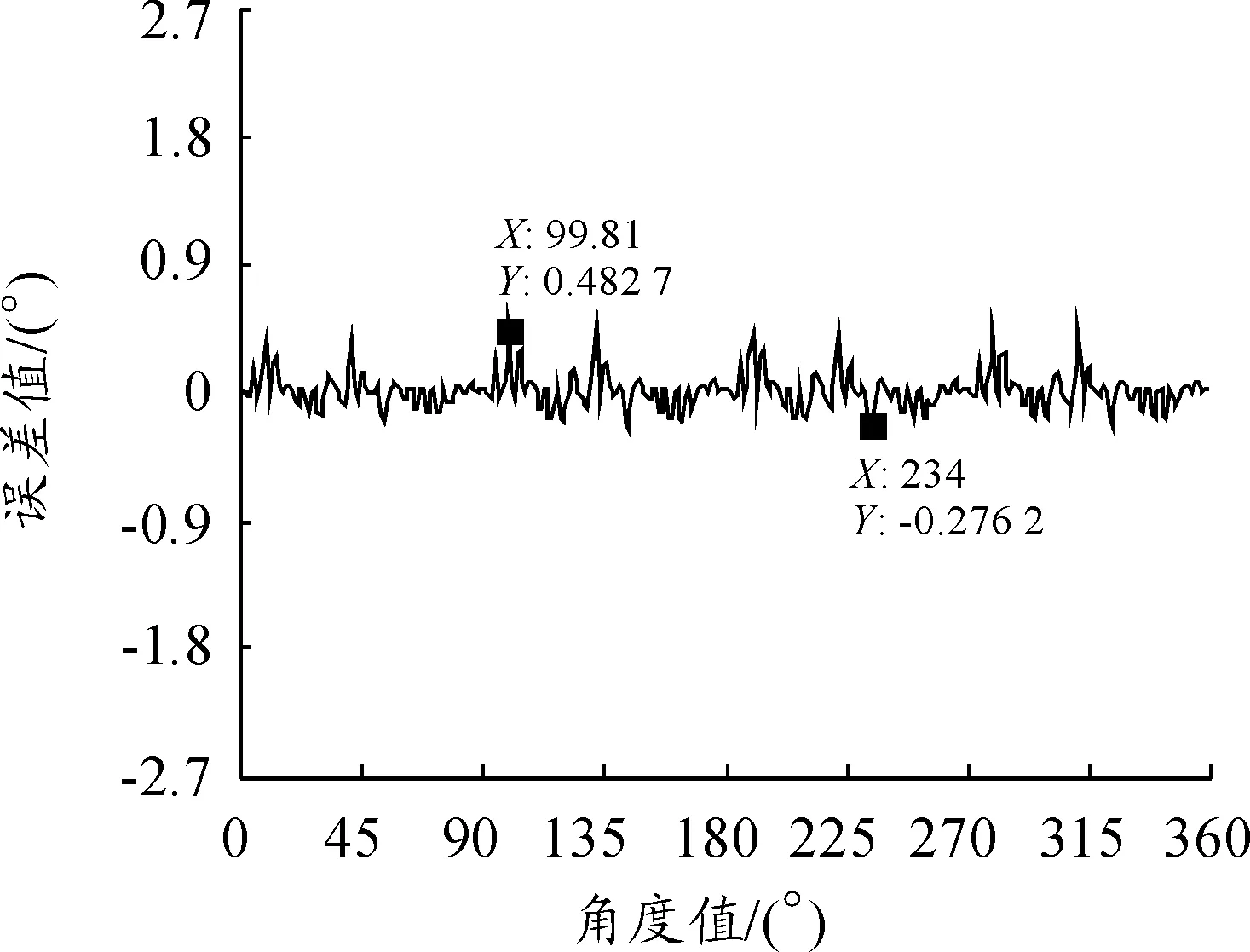
图8 修正后误差曲线

在图9(a)中对比了单对极内120 r/min转速下修正前后的误差曲线。在单对极内对修正后误差曲线进行谐波成分分析，结果如图9(b)所示，从中可以看出，在短周期内一、二次谐波误差大幅度减少，少部分高次谐波误差也被削减。由此可以说明，该方法很好地补偿了测量误差，有效地提高了伺服电机嵌入式位置检测精度。

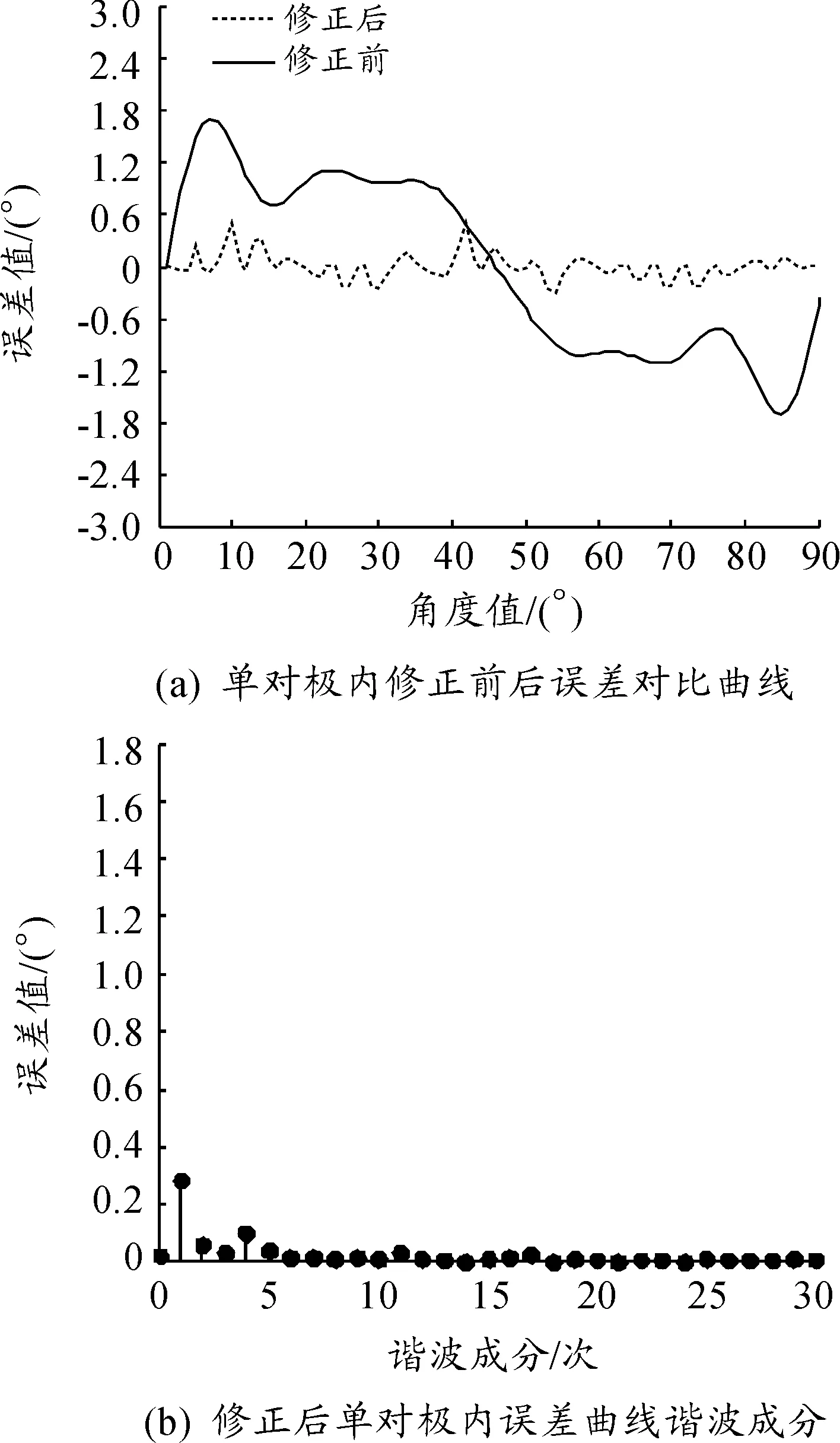
图9 单对极内修正前后误差曲线对比及修正后谐波分析

3 结论

本文在课题组前期的研究基础上，提出基于小波变换的伺服电机嵌入式位置检测误差修正方法，构建了相关算法程序流程，搭建了伺服电机位置动态检测实验系统，并借助MATLAB软件对该修正技术进行实验验证及分析。根据实验验证可以得到以下结论：

1) 测量精度明显提高，在整周的范围内测量精度从±1.8°提高到了±30′，精度提高近3.6倍。

2) 此方法凭借对误差细节的聚焦能力，很好地修正了因机械安装位置不理想而带来的检测误差。

3) 本方法不仅为永磁伺服电机嵌入式位置检测精度的提升提供了实验基础，而且为其他领域的检测方法提供新思路。