IrN的结构相变和弹性性质的第一性原理计算

李 杨，李为虎，次仁曲措，达瓦格桑，赵杏倩

(1.西藏农牧学院 公共教学部，西藏 林芝 860000；2.西北民族大学 数学与计算机科学学院，甘肃 兰州 730030)

0 引言

超硬材料一直是人们关注的热点，因为无论是石油开采、修公路用的钻头，还是精密仪器和手表表面的抗磨涂层，都需要使用超硬材料.超硬材料是指维氏硬度大于40Ga的材料.目前，自然界中最硬的材料是金刚石，它的硬度高达90 GPa[1]，但由于金刚石在空气中加热到600 ℃时就会发生氧化，且易与铁族金属发生氧化反应，因而在钢铁加工中受到很大的限制[2]，这就迫使人们寻找一种可替代的具有高热稳定性的超硬度材料.金属氮化物因其具有高硬度、脆性、高熔点、催化活性、化学惰性、超导性和光致发光性等优良性能而越来越受到实验和理论上的关注[3-7]，但目前研究大多集中于3d和4d系列中前过渡金属或后过渡金属的氮化物，而关于二元贵金属氮化物的报道却非常少见.近年来，Pt、Ir、Os和Pd等氮化物在极端条件下被人工合成[8-11]，引发了人们对新型贵金属氮化物的晶体结构、弹性稳定性和电子结构的研究兴趣.IrN是5d金属氮化合物的一种.当前，关于IrN的理论研究还较少.Chen等[12]讨论了利用第一性原理研究IrN岩盐和闪锌矿结构的弹性特性和电子结构，发现IrN在闪锌矿结构具有力学稳定性，与实验数据(IrN2，B=428GPa )[9-10]相比，IrN的体弹模量 (GGA为278 GPa，LDA为313 GPa)[12]较低.Zhao等[13]介绍了利用密度泛函理论计算IrN的结构、电子特性和力学特性.该文献分析的六种结构，即岩盐、闪锌矿、CsCl、纤锌矿、NiAs和WC结构中，发现纤锌矿结构最稳定，其次是闪锌矿结构，仅有的这两个力学稳定结构的体弹模量(闪锌矿：284 GPa，纤锌矿：253 GPa)均远小于纯金属Ir的355 GPa，根据态密度计算表明，IrN为金属.迄今为止，还没有文献报道过IrN在高压下结构相变的实验的研究.

此外，弹性常数对于固体来说是非常重要的参数，首先因为它们和各种基础的固态现象有着密切的关系，如原子间的结合键、态方程和声谱等；其次它们还和热力学性质紧密联系，如比热、热膨胀系数、德拜温度、格林乃森参数等；最后它们还与固体物质的机械性质有着紧密的关系，如加载位移、热弹性应力、内应变、声速和断裂韧性等[14-15].而研究高压等极端条件下晶体的性质,对认识晶体基本性质以及实际应用具有重要的意义，但是，到目前为止，有关高压下IrN的弹性常数的研究尚未报道.

课题组采用密度泛函理论的第一性原理赝势平面波方法，结合广义梯度近似(GGA)，通过第一性原理，计算了IrN的岩盐(B1)、氯化铯(B2)、闪锌矿(B3)、纤锌矿(B4)、NiAs (B8)和tungsten carbide(Bh)这六种结构的结构相变和弹性性质，并与之前的理论结果进行了比较.

1 理论方法

1.1 总能量电子结构计算

1.2 弹性常数

为了计算零压力下的弹性常数，本文采用了非体积守恒张力的方法.这种方法也适用于计算弹性声速.弹性常数Cijkl和有限张力变量的关系为公式(1)[19-20]:

(1)

式中σij和ekl分别表示施加的应力张量和欧拉应变张量，X和x表示坐标变形前后的坐标.

对于各向同性的压力，由公式(2)和公式(3)[20-21]决定：

(2)

(3)

这里Cijkl是对无穷小欧拉张力的二阶导数，四阶矩阵张量C一般有21个独立组元组成.然而，当考虑到晶体的对称性时，这个数字会大大减少.对于立方晶系，它们减少为三个独立的分量，即C11，C44和C12.对于六角晶系，它们只有五个独立的分量，即C11，C33，C44，C12和C13.

2 结果与讨论

2.1 晶体结构与相变

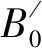
表1零温零压下IrN的晶格常数a和c、平衡体积V、弹性常数、

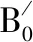
在所考虑的多晶态中，B3-IrN结构是最稳定的，其相对稳定顺序为B3类型> B4类型>B8类型> B2类型> B1类型>Bh类型.通过计算发现B3-IrN结构的能量略低于B4-IrN结构，B3和B4结构的总能量差为0.006 3 eV.这个计算结果说明，对于IrN而言，B3结构可以很容易地转变为B4结构.

热力学稳定相是在给定的压强和温度下的吉布斯自由能(G)最低的相

G=E+PV-TS

(4)

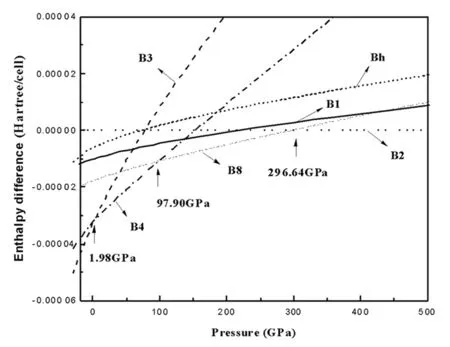
图1 T=0 K下IrN六个结构相对于B2结构的焓差随压强的变化关系

其中E、S、P和V分别表示内能、熵、压强和体积.理论计算是在T=0 K条件下进行的，因此，吉布斯自由能G与焓H相等，即H=E+PV，其中P=-∂E/∂V.一般来说，计算相变压强的方法是通过找任意两个相的能量曲线的公切线来找相变压强，但是这种方法操作起来很困难而且会有很大的误差.因此，本文计算了IrN六个结构(B1、B2、B3、B4、B8和Bh)对应的焓，考虑到任意两个结构之间的焓具有很细微的差值，据此绘出焓差与压强之间的关系,如图1所示.从图1中可以发现,B3→B4→B8→B2的结构相变压强分别发生在1.98 GPa，97.90 GPa和296.64 GPa.而现有文献尚未找到可供与IrN结构相变比较的其他数据，因此，本文的结果可作为将来研究的一个理论参考.

此外，为了更加深入地理解IrN随压强变化结构性质，本文对B4结构在0～85 GPa的压强范围内进行了结构优化，在图2中绘出了晶格常数的比率a/a0，c/co和体积的比率V/V0与压强的关系.从图2能够看出，随着压强的增大，原胞体积的比率从1变化到 0.823，而晶格常数比率a/a0，c/co也随压强的增大单调递减，显然a/a0较c/co随压强增大下降得更快．这说明B4-IrN沿着晶体的a轴方向比沿着c轴方向更容易被压缩，IrN这种明显的各向异性压缩行为将会导致不同的压强对声子模式的影响，并且也会引起费米能级附近的电子结构发生改变.

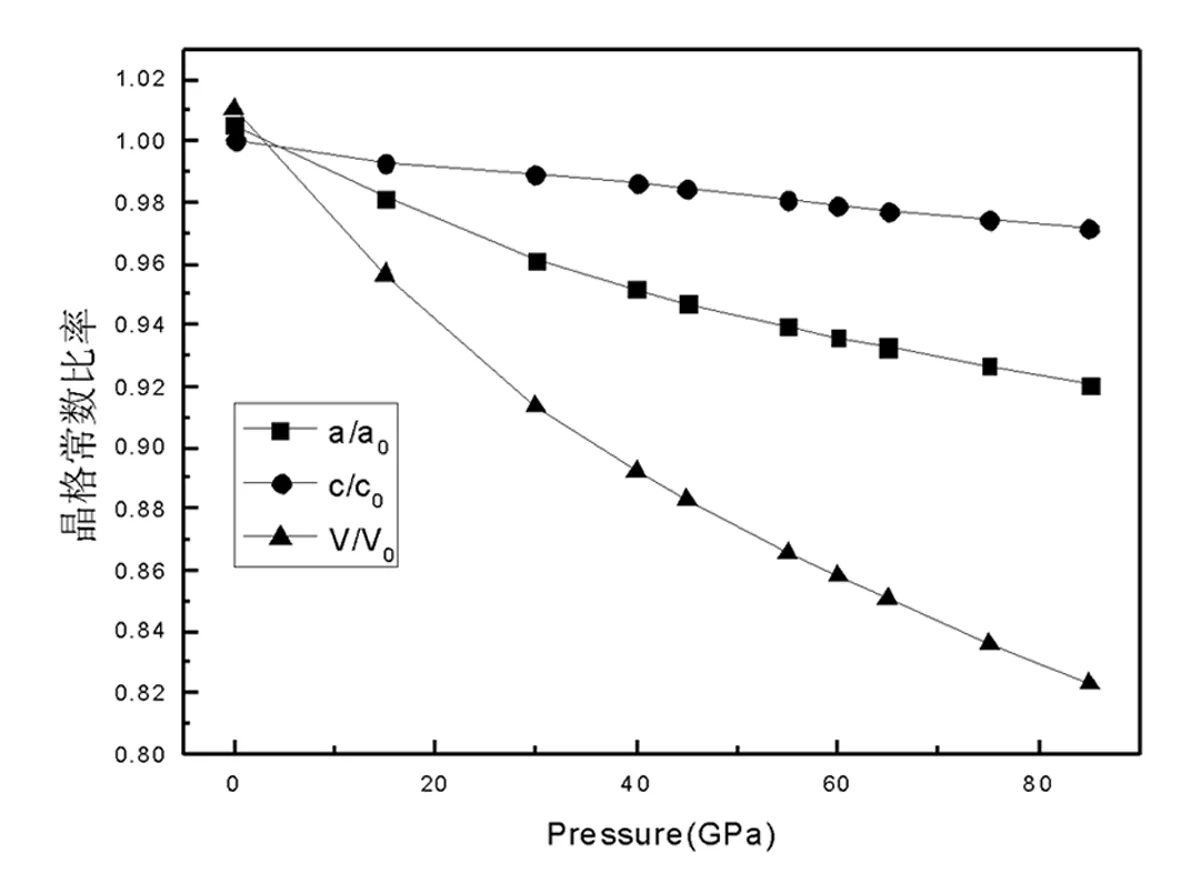
图2 晶格常数比率随压强的变化关系

2.2 弹性性质

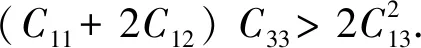
根据Voigte-Reuss-Hill (VRH)平均算法[23]，利用弹性常数可以得到体弹模量B和剪切模量G.对于立方晶系和六方晶系，体弹模量BV和BR以及剪切模量GV和GR都可以从参考文献[22]给出的关系式求得(V表示的是Voigte约束，R表示的是Reuss约束)，Voigte和Reuss约束的平均算法被称作Voigte-Reuss-Hill近似[24]：

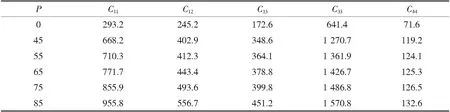
表2T=0K下IrN的B4相弹性常数Cij(GPa)与压强的关系

(5)

计算出体弹模量和剪切模量后，可由此得出压缩波速υp、剪切波速υs以及平均波速υm：

(6)

(7)

式(6)中ρ表示密度.在图3和图4中，给出了体弹模量B、剪切模量G、压缩波速υp、剪切波速υs和平均波速υm随压强的变化关系，显然，体弹模量、剪切模量、压缩波速、剪切波速和平均波速都随着压强的增大而单调递增.

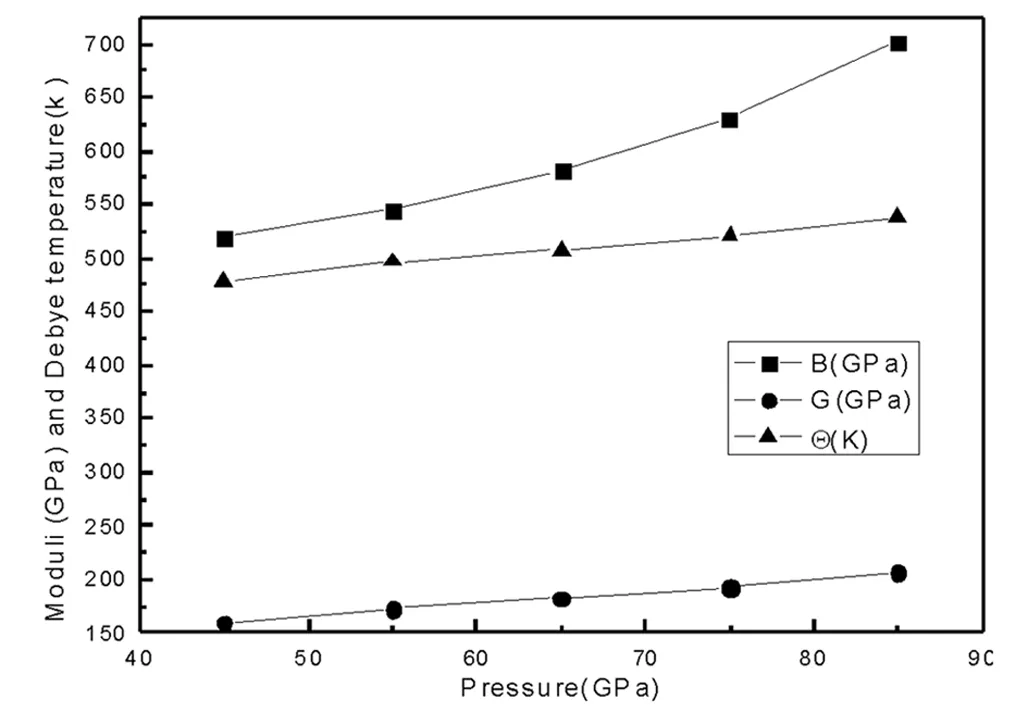
图3 B4-IrN结构的体弹模量、剪切模量以及德拜温度与压强的关系

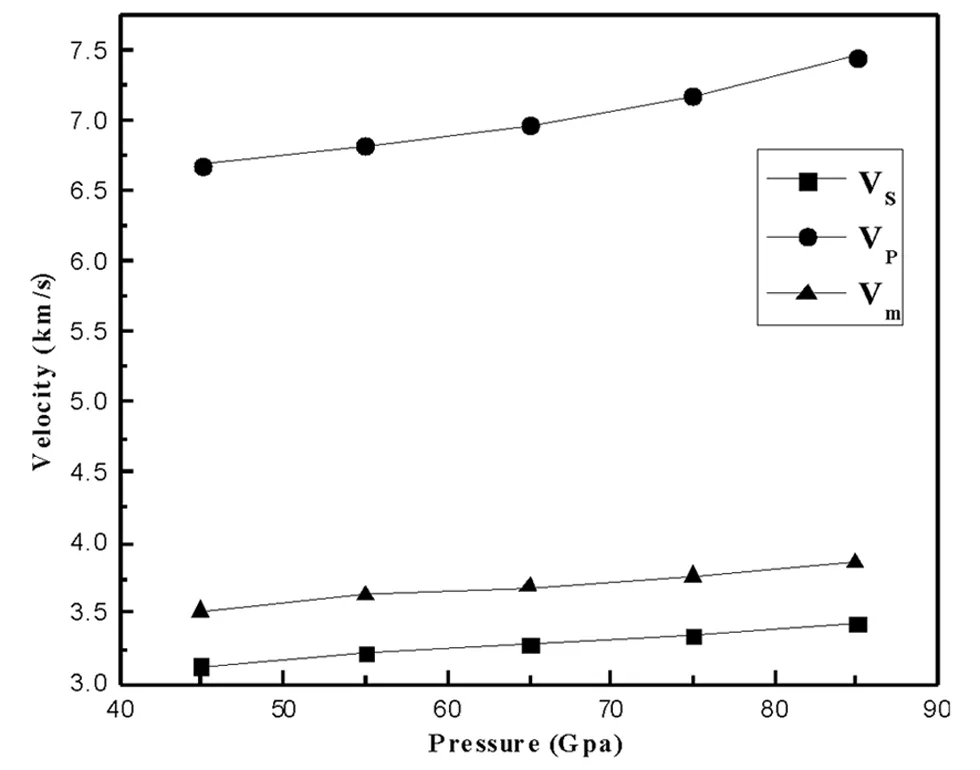
图4 B4-IrN结构的声速随压强的变化关系

为更全面了解B4结构的弹性特性，本文还使用公式(8)计算了泊松比υ：

(8)

利用上述关系计算出的体弹模量B、剪切模量G、杨氏模量Y和泊松比υ,详见表3所示.

表3不同压强下B4结构的体弹模量B(GPa)、剪切模量G(GPa)、杨氏模量Y(GPa)和泊松比v

为了预测固体的脆性和韧性，Pugh[25]提出了一个衡量材料的韧性或脆性的体弹模量与剪切模量的比值(B/G)的简单关系式，即B/G的值高对应韧性，而低比率则对应脆性.并且Pugh[25]给出了韧性-脆性转变的临界值，如果B/G<1.75，那么这种材料就表现为脆性，反之则表现为韧性.对于IrN在0 K和0 GPa下的B4结构，本文计算出的B/G值是4.39(见表3)，表明该材料表现为韧性.随着压强从45 GPa增加到85 GPa，B/G比值均在3.20附近变化，其值总是大于1.75，这说明B4结构始终保持着韧性.此外，Frantsevich[26]提出了一种用泊松比来判别材料脆性和韧性的方法.根据Frantsevich的理论方法，材料泊松比的临界值是1/3，对于某种固体材料，如果它的泊松比大于1/3，这种材料展现出韧性，反之，展现脆性.通过得到的B4结构泊松比(见表3)，泊松比随着压强的变化在0.360附近变化，都大于1/3，说明该结构在所选取的压强范围内都呈现韧性，与采用B/G方法所预测的结果完全一致.

弹性各向异性在工程科学和晶体物理学中有着重要的应用，高压下的弹性各向异性对于理解固体中原子键的演化过程有着重要的意义.表4列出了不同压强下B4结构各向异性因子的变化情况，对于六方晶体，弹性各向异性ΔP、ΔS1和ΔS2可以通过下面的公式给出[27]：

ΔP=C33/C11

(9)

ΔS1=(C11+C33-2C13)/4C44

(10)

ΔS2=2C44/(C11-2C12)

(11)

其中，ΔP、ΔS1和ΔS2分别是相对于压缩波和两个剪切波的各向异性.对于某种固体材料来说，若ΔP=ΔS1=ΔS2=1，则说明该材料为弹性各向同性，反之为各向异性.计算得到的不同压强下的ΔP、ΔS1和ΔS2在图5中给出.从图中可以看出，ΔP和ΔS2随着压强增加而下降，ΔS1则随着压强的增大而递增.

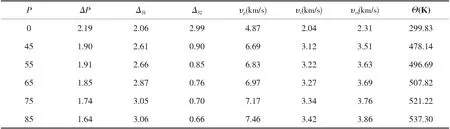
表4不同压强下B4-IrN结构的各向异性因子(ΔP，ΔS1，ΔS2)、压缩波速υp、

剪切波速υs、平均声速υm和德拜温度Θ

2.3 德拜温度

德拜温度Θ是一个非常重要的物理量，它与固体的许多物理性质密切相关，如：比热容、弹性常数、导热系数以及熔点等.从弹性常数出发，可以获得德拜温度，因为德拜温度可通过平均声速υm推出[28]：

(12)

其中，h是普朗克常数，κ是玻尔兹曼常数，NA是阿伏伽德罗常数，n是单位体积的原子数，M是分子质量，ρ为密度，晶体的平均声速υm可由公式(7)求得.本文计算出的零温零压下B4-IrN结构的德拜温度为299.83 K，结果详见表4.从表4可以看出,德拜温度随压强的增大单调递增.遗憾的是到目前为止还没有其他的理论和实验值能够进行对比.此外，图3给出了B4-IrN结构的德拜温度随压强的变化关系.从图3可以看出,德拜温度随压强的增大而单调递增.

3 结论

基于密度泛函理论对IrN的结构相变进行了预测，发现IrN的相序为B3→B4→B8→B2，得到的相变压强分别1.98 GPa，97.90 GPa和296.64 GPa.通过计算比较，发现B3结构在0 GPa时最稳定.还对B4结构在高压下的弹性常数进行了预测，得到了体弹模量、剪切模量、杨氏模量、压缩波速度和剪切波速度等.结果表明，体弹模量、剪切模量、杨氏模量、压缩波速度和剪切波速度均随压强的增大而单调增加.根据对B/G的分析，发现B4结构在压力下也保持着一定的韧性.此外，为更全面地了解IrN的弹性特性，本文还对泊松比、弹性各向异性和德拜温度进行了理论预测，希望该研究结果有助于进一步的实验研究.