空间两直线相关位置的探究

郑 惠

(阿坝师范学院 数学与计算机科学学院，四川 汶川 623000)

0 引 言

判定空间两直线相关位置是解析几何中一项重要内容.由于两直线方程的表现形式可以有多种情形：两条直线方程均为标准方程；一条直线方程为标准方程、另一条直线方程为一般方程；两条直线方程都为一般方程；甚至还可以是参数方程等.文献[1-3]在空间两直线方程均为标准方程的基础上详细介绍了空间两直线异面、相交、平行、重合的充要条件,但一般方程的情形并没有讨论.文献[1-3] 作为教材依旧为读者继续探讨两直线间的相关位置留下了较大的思索空间. 文献[4-11]分别用不同的方法对不同的情况进行了研究,文献[9]就“一条直线方程为标准方程、另一条直线方程为一般方程”的情形进行了研究，但是给出了一个错误的异面直线的距离公式以及两共面直线相交、平行的充分不必要条件为充要条件.本文将再次讨论此情形下两直线的位置关系，给出两直线异面、相交、平行、重合的充要条件以及异面直线间的距离公式.

1 定理及证明

定理1设空间两直线的方程分别为：

1)异面：Δ=N(A1X+B1Y+C1Z)-M(A2X+B2Y+C2Z)≠0

2)相交：Δ=0，且(A1X+B1Y+C1Z)2+(A2X+B2Y+C2Z)2≠0

3)平行：A1X+B1Y+C1Z=A2X+B2Y+C2Z=0，且M2+N2≠0

4)重合：A1X+B1Y+C1Z=A2X+B2Y+C2Z=0，且M2+N2=0，其中M=A1x0+B1y0+C1z0+D1,N=A2x0+B2y0+C2z0+D2.

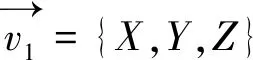
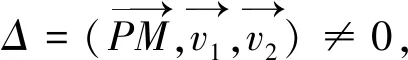
=[(A1x1+B1y1+C1z1)-(A1x0+B1y0+C1z0)](A2X+B2Y+C2Z)

-[(A2x1+B2y1+C2z1)-(A2x0+B2y0+C2z0)](A1X+B1Y+C1Z)

=N(A1X+B1Y+C1Z)-M(A2X+B2Y+C2Z).

故直线l1与l2异面的充要条件为：

Δ=N(A1X+B1Y+C1Z)-M(A2X+B2Y+C2Z)≠0；

共面的充要条件为：Δ=0.

又当两直线共面时，有以下三种情况：

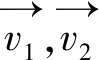
Δ=0，且(A1X+B1Y+C1Z)2+(A2X+B2Y+C2Z)2≠0.

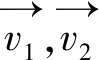
A1X+B1Y+C1Z=A2X+B2Y+C2Z=0,且M2+N2≠0.

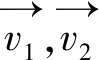
A1X+B1Y+C1Z=A2X+B2Y+C2Z=0,且M2+N2=0.