基于EMD和CICA的单通道盲源分离方法用于齿轮箱混合故障诊断研究

郝如江，安雪君，史云林

(石家庄铁道大学 机械工程学院，石家庄 050043)

机械设备结构复杂，组成部件较多，齿轮箱作为其中重要的传动部件，对其进行故障诊断具有重要意义。振动信号分析技术是对机械设备进行故障诊断与状态检测的重要方法之一，已形成比较完备的理论与技术体系，在齿轮箱故障诊断中常用的信号处理方法有：经验模式分解[1]、小波变换[2]、局部均值分解[3]等方法，这些经典的方法可在一定程度上实现对观测数据的预处理，从而获取齿轮箱的故障信息。

盲源分离(Blind Signal Separation，BSS)是实现机械设备故障诊断的有效方法之一[4]，该方法的特点在于不依赖任何先验知识，利用设备各故障信号和噪声信号的相对独立性，将源信号从观测信号中分离出来。传统的盲源分离方法，如独立分量分析方法(Independent Component Analysis，ICA)，要求信号接收器的数目不少于源信号的数目[5]，这在工程实践中往往难以实现。约束独立分量分析方法(Constrained Independent Component Analysis，CICA)由ICA发展而来，该方法的关键是在ICA基础算法中引入有效的约束条件[6]，使ICA算法向着约束条件所要求的方向收敛，进而提取感兴趣的独立分量。国内陈进、王志阳、梁瑜等将CICA应用到滚动轴承的故障诊断，成功提取出了滚动轴承故障特征[7-9]。经验模式分解(Empirical Mode Decomposition，EMD)可实现对一维信号的自适应分解，产生一系列本征模式分量(Intrinsic Mode Function，IMF)[10]。Wu等[11]应用EMD方法研究了归一化白噪声的统计特性，提出一种新颖的振动模式提取方法。本文将EMD算法引入混合故障盲源分离中，提出了基于EMD与CICA的齿轮箱混合故障单通道盲源分离方法。通过EMD分解对单通道信号进行预处理，从而解决了盲源分离时的欠定问题，实现齿轮箱混合故障的特征提取。

1 基于白噪声统计特性和峭度值的EMD方法

1.1 EMD原理

EMD方法是通过对非线性、非平稳信号的分解获得一系列表征信号特征时间尺度的固有模态函数[12]。对于一个给定的信号x(t)，经EMD算法分解后可得到一系列IMF分量ci(t)，直到rn(t)满足EMD分解的终止条件，结束筛选过程。IMF分量筛选过程结束后，原信号可表示为

(1)

在上述EMD分解中，由于EMD自身分解规则存在缺陷，导致得到的IMF分量中存在虚假模式分量，会对后续的故障特征提取造成影响，因此需要对IMF分量进行筛选。

1.2 基于白噪声统计特性的IMF筛选方法

一组归一化随机白噪声时间序列nm，m=1,…，N。对其进行EMD分解后表示为

(2)

式中：cl(m)为第l个IMF分量，定义cl(m)的能量密度为

(3)

Wu等发现，对于第一个IMF除外的任意IMF分量，其Fourier谱的函数形式均可表示为

(4)

式中：Sln T,l为cl(m)的Fourier谱；const为常数。

为衡量各IMF分量的Fourier谱和能量之间的关系，cl(m)的能量为

(5)

式中：Sw,l为cl(m)关于频率ω的Fourier谱。

将式(4)代入式(5)，可得到任意cl(m)的能量密度和平均周期Tl的关系为

(6)

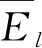
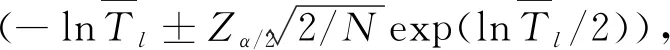
1.3 基于峭度的IMF筛选方法

峭度是反映振动信号分布特性的数值统计量，对冲击类故障信号的反应比较准确。机械正常运转时，其振动信号近似服从正态分布，其峭度值约为3。当有故障出现，大幅值振动信号的概率密度增加，信号幅值的正态曲线会出现偏斜或分散，峭度值随之变大。而峭度指标的绝对值越大，说明包含的故障信息越多，因此，当某些IMF分量的峭度值大于3时，说明其中保留了较多的故障冲击成分，可以以此作为IMF有效振动模式提取的参考准则。峭度的定义如式(7)所示

(7)

式中：μ和σ分别为振动信号x(t)的均值和标准差；E为数学期望。

2 约束独立分量分析(CICA)

CICA算法是建立在ICA基础上，将源信号的先验知识作为约束函数(参考信号)，提取出和参考信号最相似的一个独立分量。基于源信号已知信息构造参考脉冲信号r(t)，将待提取的目标成分y和参考信号r(t)的距离函数定义为ε(y,r)，用以表示目标成分和参考信号的接近程度。ε(y,r)可用均方误差ε(y,r)=E{(y-r)2}度量，CICA算法的数学模型如式(8)及式(9)所示

目标函数

maxJ(y)≈ρ{E[G(y)]-E[G(v)]}2

(8)

约束条件

(9)

式中：ρ为正常数；G(·)为非线性函数；v为具有与y相同协方差矩阵的高斯变量；ξ为阈值。式(9)实际上是一个约束优化问题，通过拉格朗日乘数法对其求解，可得到源信号的最佳估计，提取出目标源信号。

3 基于EMD和CICA的混合故障盲源分离

为从齿轮箱轴承与齿轮故障信号中提取出目标源信号，提出一种EMD和CICA相结合的方法，具体故障特征提取方法流程图，如图1所示。首先将单通道采集到的数据进行EMD分解，利用各IMF的白噪声统计特性和峭度值对比结合方法，选取出有效的振动模式分量作为下一步盲源分离的输入信号。将故障齿轮及轴承的先验信息，即故障特征频率作为参考信号，最后通过CICA算法提取感兴趣的故障信号，诊断出齿轮及轴承的故障信息。

图1 故障特征提取方法流程图Fig.1 Flowchart of fault feature extraction method

4 试验验证

4.1 仿真数据实验

为了验证上述方法在分析齿轮箱混合故障特征提取中的有效性，构造一组仿真信号。其中，s1为轴承外圈故障仿真信号，s2为齿轮故障仿真信号，s3为混入的白噪声信号，采样频率为25 600 Hz，s1及s2如式(10)所示。仿真信号时域波形如图2所示。

(10)

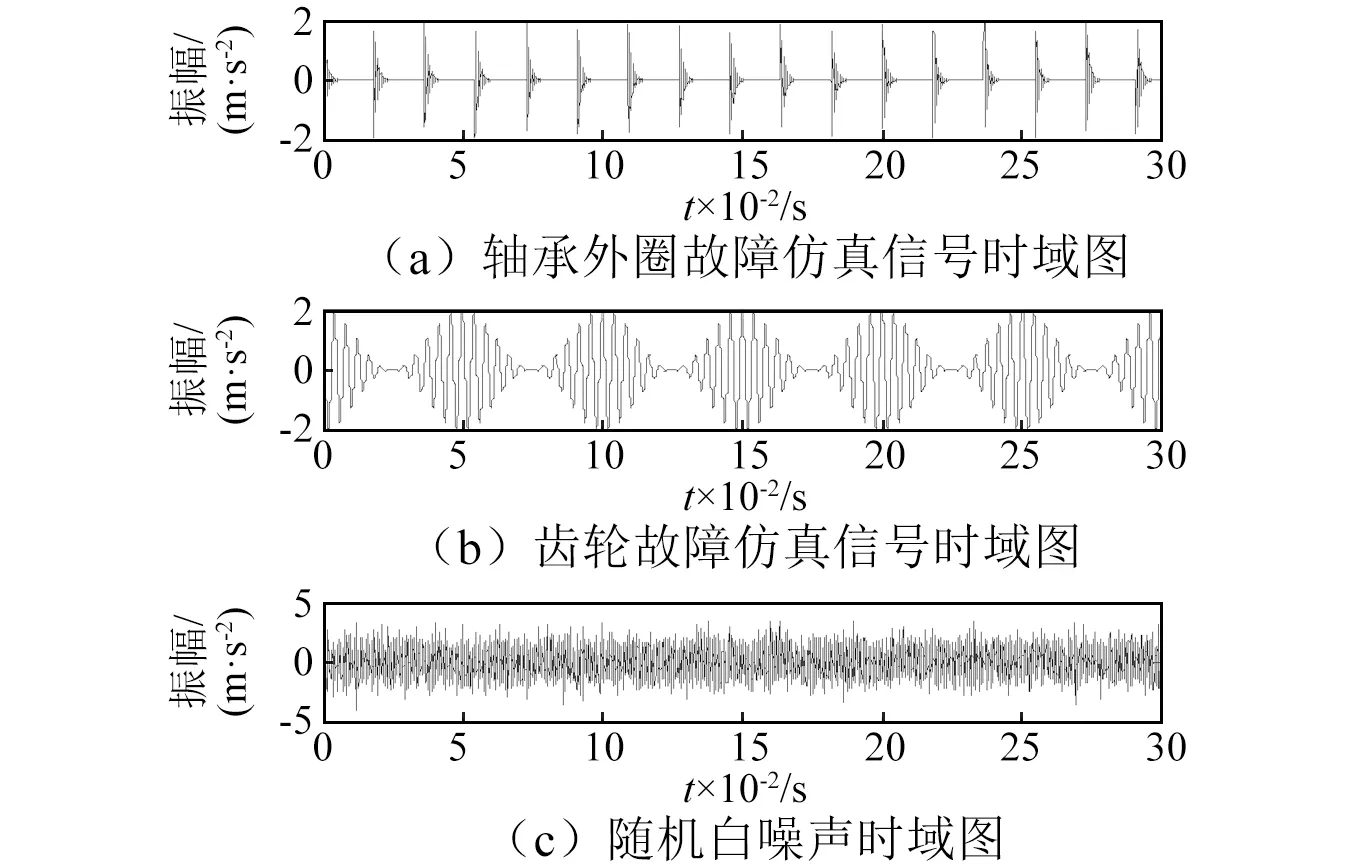
图2 仿真信号时域波形Fig.2 Time-domain waveform of simulation signal

式中：N为冲击个数;仿真时长t=0.5 s;fm=55 Hz为周期性冲击信号的频率即仿真轴承的故障特征频率;h(t)为单个冲击函数，见式(11)；f2=240 Hz为故障齿轮啮合频率；仿真故障齿轮幅值调制频率fz为20 Hz。

(11)

式中：a=400为衰减率；冲击幅值A=2 m·s-2；f1=3 000 Hz仿真轴承冲击导致的共振频率。

将以上信号进行混合，仿真单通道数据。对归一化处理后的混合信号进行EMD分解，得到13个IMF分量。构造与仿真信号等长度的归一化白噪声样本模板图，将仿真信号分解出的各IMF分量的能量密度和平均周期对数值(用*表示)与该模板中置信区间对比，结果如图3所示。IMF1，IMF2，IMF5，IMF6及IMF7落在置信区间外，其中IMF1虽落在置信区间外，但符合白噪声模板中第一个IMF集合的分布特点，可判断出IMF1属于高频噪声分量。计算各IMF的峭度值，如图4所示。从图4可知，IMF2，IMF5，IMF6，IMF7及IMF11的峭度值大于3，将白噪声统计特性与峭度值方法相结合，最终判断IMF2，IMF5，IMF6及IMF7属于振动模式分量。将选取出的IMF分量进行重构，其时域图与原信号对比，如图5所示。从图5可知，对信号进行EMD分解再重构实现了一定程度上的降噪处理，冲击成分更加明显。

图3 仿真信号各IMF的白噪声统计特性分布Fig.3 IMF’s white noise characteristics of simulation signal

图4 仿真信号各IMF的峭度值Fig.4 IMF’s kurtosis values of simulation signal

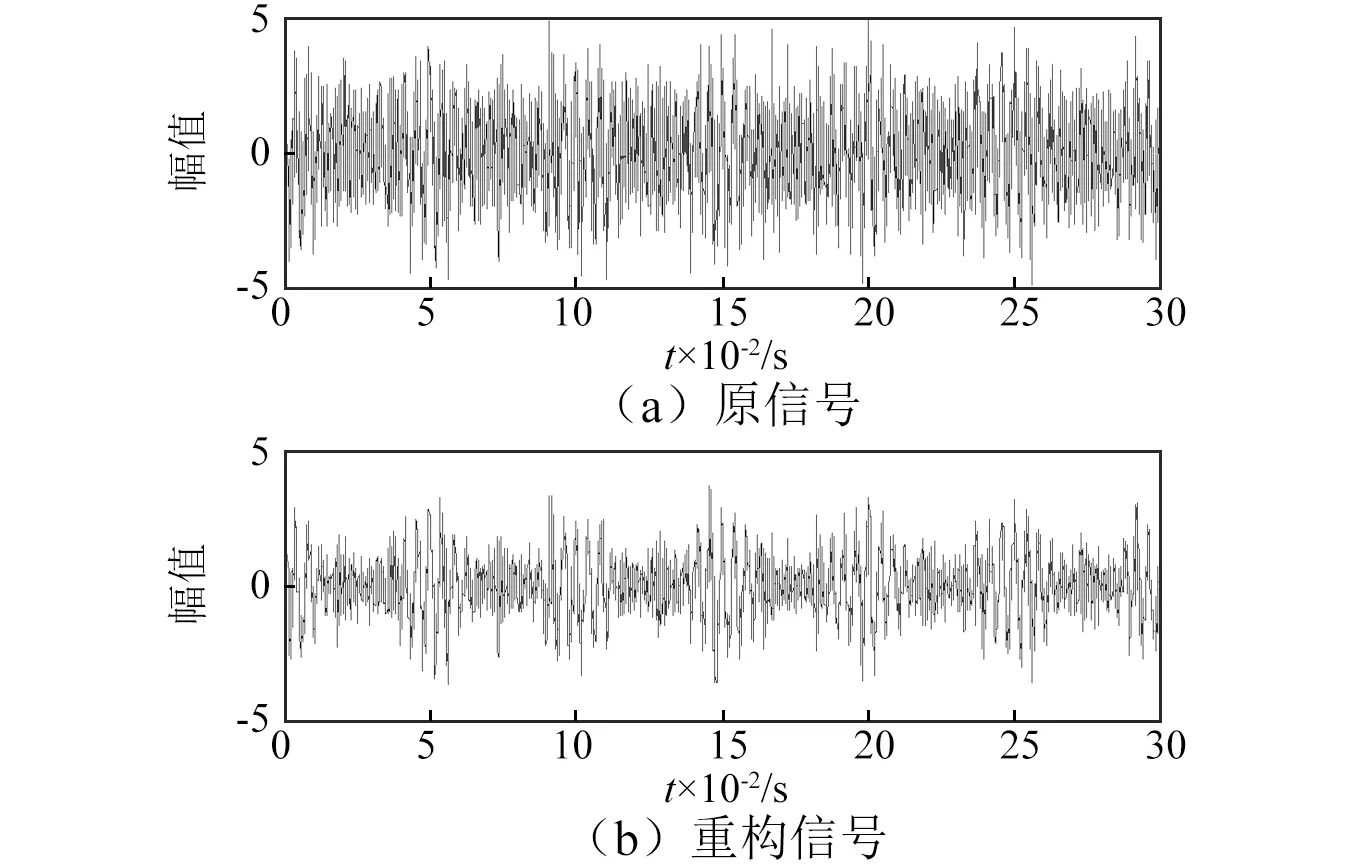
图5 原信号与重构信号的时域对比图Fig.5 Time-domain comparison of original signal and reconstructed signal

利用CICA算法对筛选出的IMF分量进行盲源分离，目的将轴承及齿轮故障仿真信号从选取的IMF分量信号中提取出来。将IMF2，IMF5，IMF6及IMF7作为四维输入信号，如图6所示。参考轴承及齿轮仿真故障特征频率，建立方波形式的参考信号，并利用CICA方法提取出的轴承及齿轮仿真故障信号时域波形，如图7所示。为更清楚地分析已提取出的信号，对分离出的目标信号分别做Hilbert包络分析，得到Hilbert包络谱如图8所示，从图8可知，对应的轴承仿真故障频率55 Hz以及倍频，以及齿轮仿真故障的调制频率20 Hz，验证了上述选取IMF分量方法以及CICA算法在混合故障特征提取中的有效性和可行性。

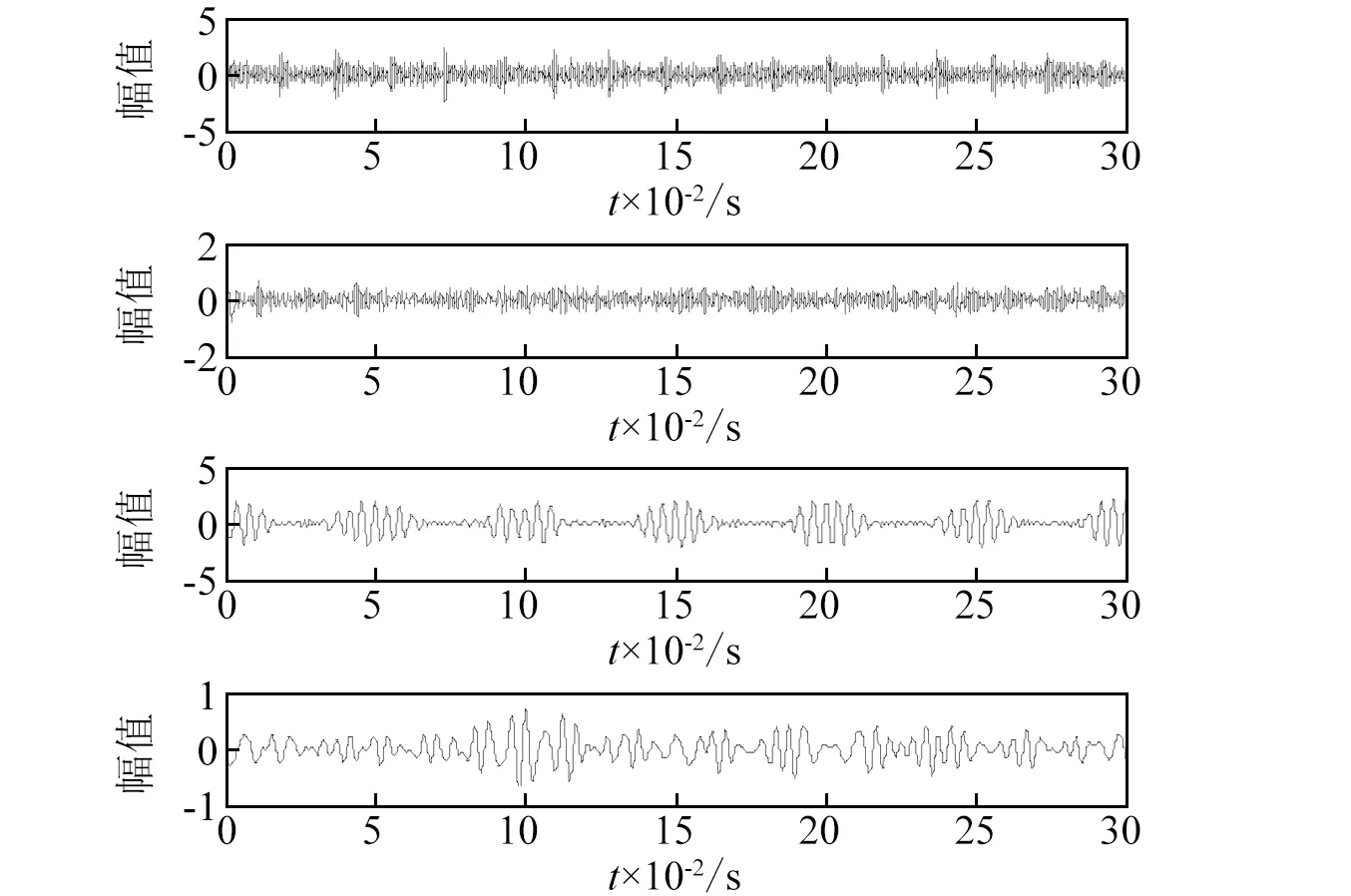
图6 选取出的IMF分量Fig.6 The selected IMF components

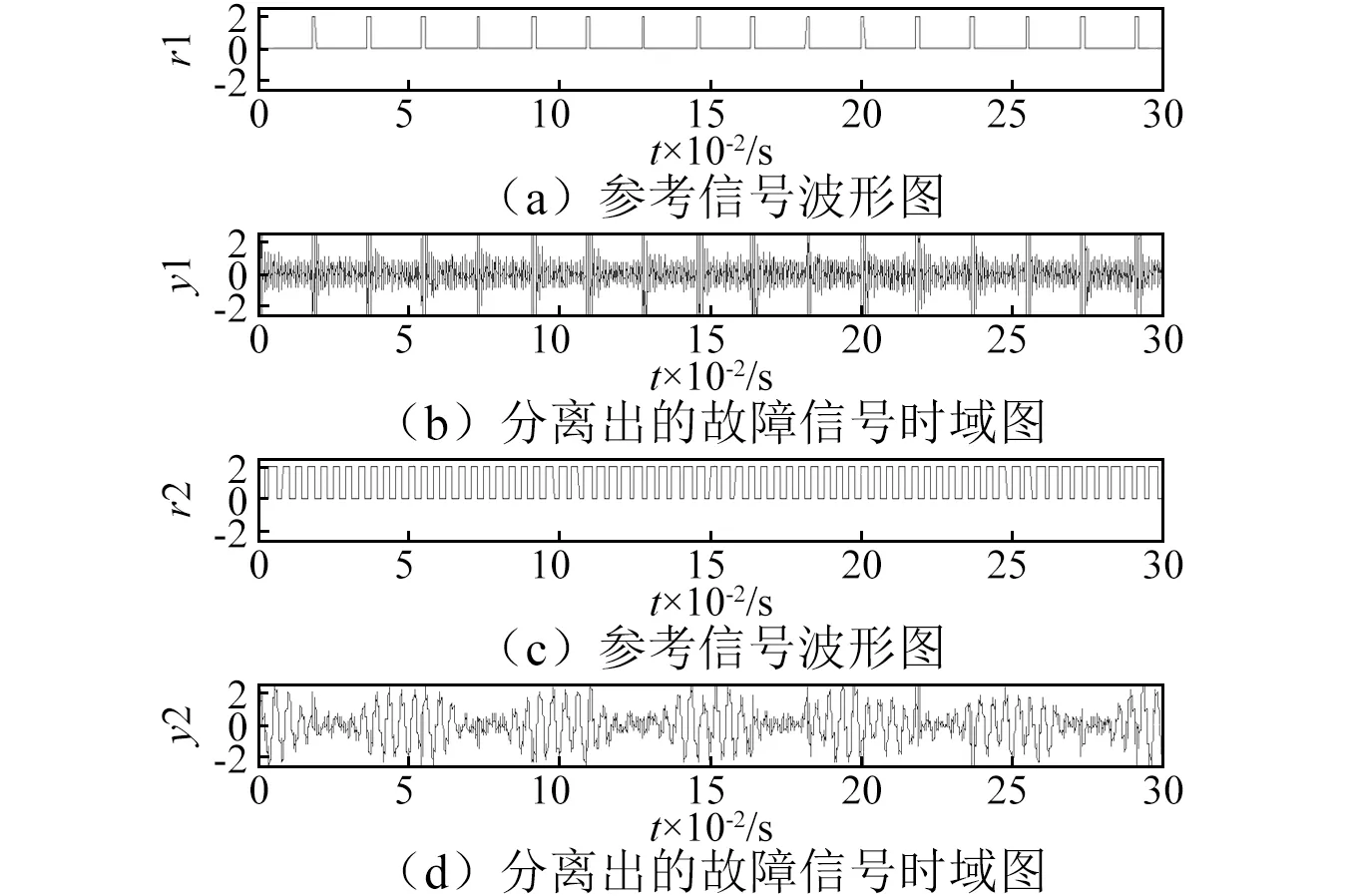
图7 参考信号及分离出的故障信号时域波形Fig.7 Reference signal and time-domain waveform of isolated fault signal

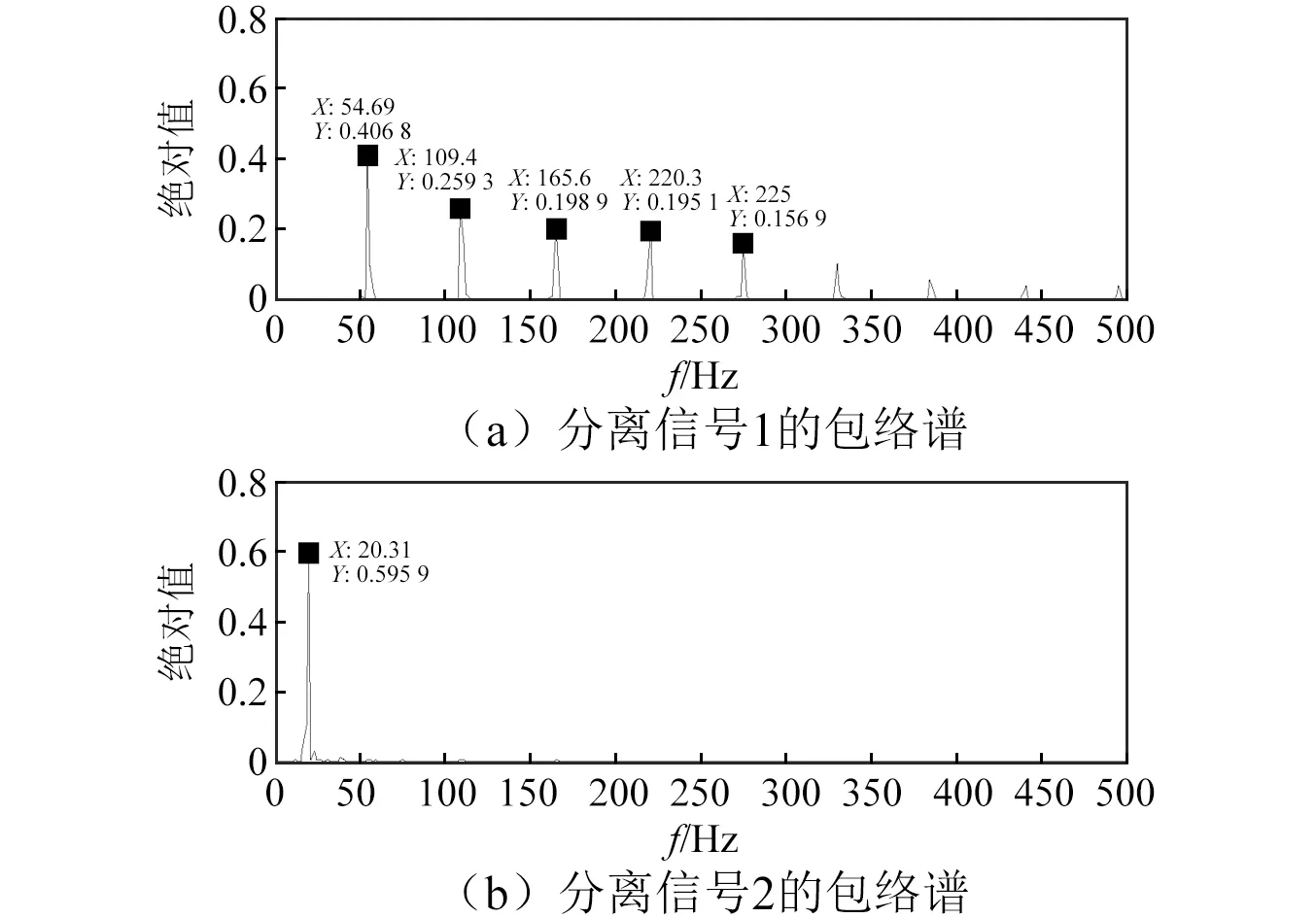
图8 分离信号的包络谱Fig.8 Envelope spectrum of isolated signal

4.2 齿轮箱实测数据及分析

为验证上述方法对实际测试信号的有效性，采用SpectraQuest公司设计的可模拟工业动力传动的故障诊断综合实验台(DDS)进行实验分析。如图9所示。动力传动系统由一个1级行星齿轮箱，一个2级平行轴齿轮箱，一个轴承负载和一个可编程的磁力制动器组成，齿轮箱的传动系统图如图11所示。故障齿轮及轴承均位于平行齿轮箱内的中间轴上，电机输入转速为2 400 r/min，传递到平行齿轮箱中间轴的转频为2.537 Hz，齿轮为断齿故障，齿数为36，啮合频率为91.35 Hz；轴承采用61800型滚动轴承，内圈故障，其基本参数如表1所示。计算得到内圈故障特征频率为13.78 Hz。单通道传感器布置在靠近故障轴承的轴承座外壳上(垂直方向)，如图10所示。利用DASP数据采集仪采集数据，采样频率为25 600 Hz，总采样时长为10 s，截取其中2 s数据进行分析。

表1 故障轴承几何参数Tab.1 Geometric parameters of fault bearing

图9 DDS实验台Fig.9 DDS test platform

图10 传感器安装位置Fig.10 Location of the sensor

首先采集正常齿轮箱的单通道振动数据，时域波形及其幅值谱和Hilbert包络谱，如图12所示。幅值谱中可见较明显的峰值为39.84 Hz和91.02 Hz，接近电机输入转频40 Hz和中间轴上齿轮的啮合频率91.35 Hz；包络谱可观察到较明显的峰值为8.594 Hz，接近平行齿轮箱高速轴的转频8.75 Hz。可见齿轮箱在正常工作时，由于该实验台传动系统较复杂，上述频率比较突出，不可避免。采集局部断齿及轴承内圈的单通道混合故障信息，时域波形及其幅值谱和Hilbert包络谱，如图13所示。与正常齿轮箱相比，混合故障时域波形有明显冲击，其幅值谱中齿轮啮合频率91.41 Hz更加突出，包络谱中可观察到平行齿轮箱中高速轴转频8.984 Hz(理论值8.75 Hz)，中间轴(故障所在轴)转频约2.34 Hz(理论值2.53 Hz)，但与高速轴转频对比而言幅值较小；频率成分较复杂，由于轴承内圈故障十分微弱，幅值谱及包络谱中均无法识别出轴承内圈故障信息(理论值13.78 Hz)。

图12 正常齿轮箱信号分析Fig.12 Signal analysis of normal gearbox

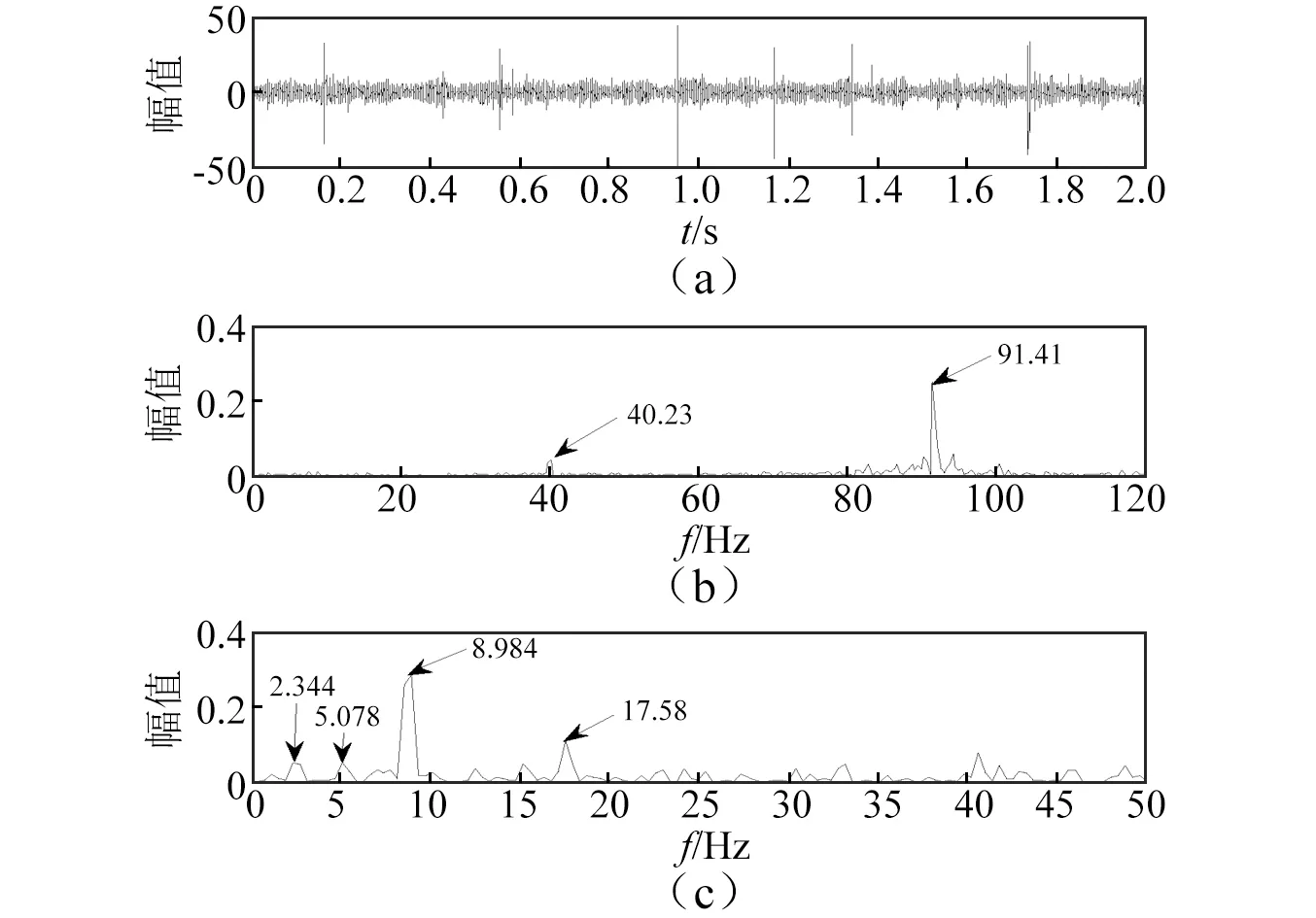
图13 混合故障齿轮箱信号分析Fig.13 Signal analysis of gearbox with multi-fault

对单通道信号进行EMD分解，得到14个IMF分量，基于白噪声统计特性及峭度值原则对IMF分量进行筛选。各IMF的能量密度和平均周期对数关系表示在白噪声统计模板中，如图14所示。计算各IMF的峭度值如图15所示。根据上文中叙述的根据白噪声统计特性选取振动模式分量的原则，并结合峭度值筛选原则，选择落在白噪声统计模板的置信区间外，同时满足峭度值大于3的IMF分量，最终确定IMF2，IMF5以及IMF6作为筛选出的振动模式分量。

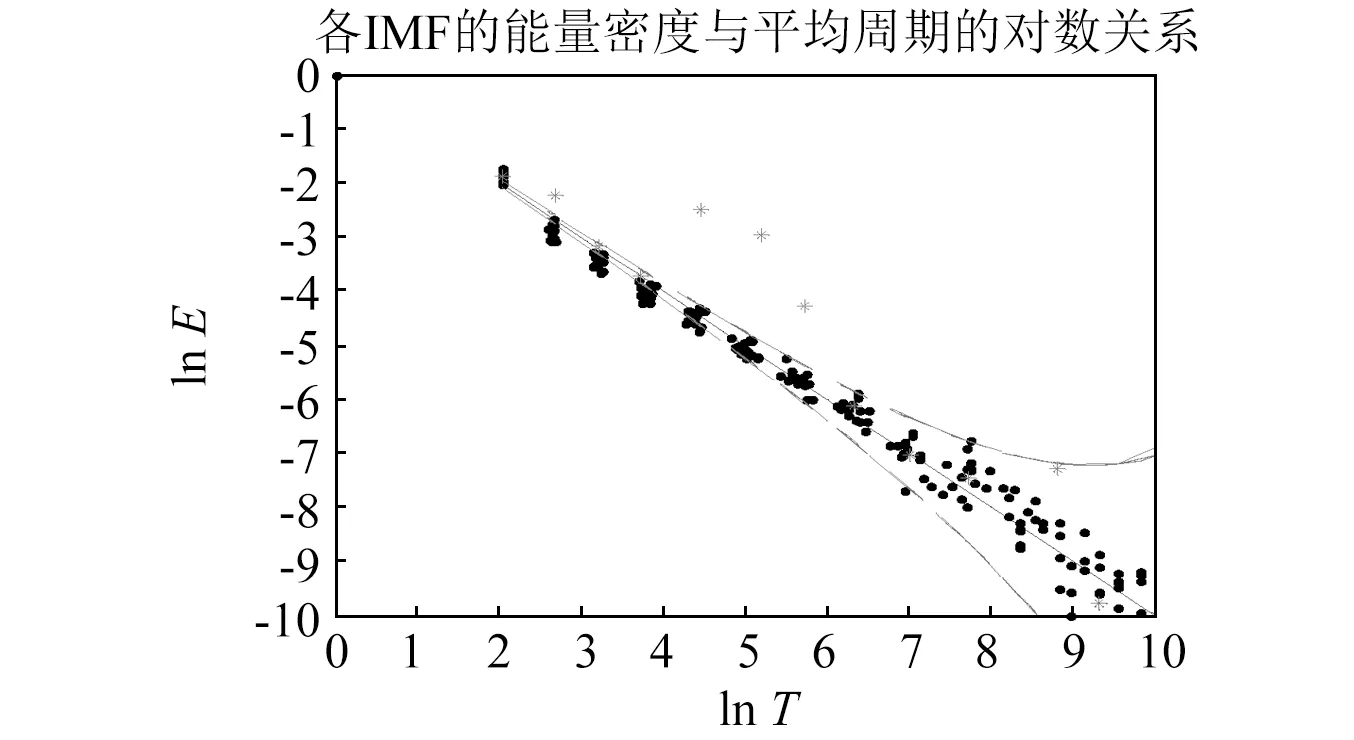
图14 实测信号各IMF的白噪声统计特性分布Fig.14 IMF’s white noise characteristics of experimental signal

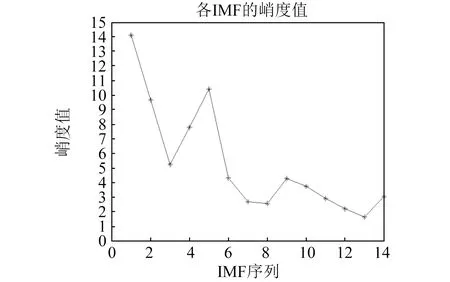
图15 实测信号各IMF的峭度值Fig.15 IMF’s kurtosis values of experimental signal

对IMF分量进行筛选，去除了由EMD分解出的高频噪声分量以及虚假振动模式，所选择的IMF分量包含了齿轮箱混合故障信息，在一定程度起到了降噪作用。对数据进行EMD降噪后，传统分析方法是将选取的分量IMF2，IMF5和IMF6重构，对其进行Hilbert包络分析，得到故障特征频率。按照此方法所得包络谱如图16所示。从图16可知，高速轴转频的干扰依然很严重，故障轴承的特征频率(理论值13.78 Hz)十分微弱，故障齿轮所在轴的转频(理论值2.53 Hz)几乎不可辨，说明直接对重构信号进行Hilbert包络的方法对于提取轴承及齿轮的故障特征频率效果并不显著。

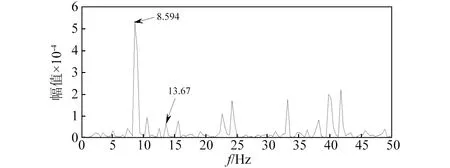
图16 重构信号的包络谱Fig.16 Envelope spectrum of reconstructed signal

利用ICA算法对信号进行分析，将IMF2，IMF5和IMF6作为ICA算法的输入信号，时域波形如图17所示。经过ICA算法得到3个分离信号，对其分别进行幅值谱和包络谱分析，见图18和图19。图18(b)的幅值谱中可见突出的频率峰值为91.41 Hz，接近故障齿轮的啮合频率，但峰值两侧并未出现明显的边频成分。图19(a)和图19(b)对应的包络谱中分别可观察到故障轴承的特征频率(理论值13.78 Hz)和故障齿轮的转频(理论值2.53 Hz)，但是在其周围均存在较强的其他频率成分；图19(c)中对应的包络谱可见平行齿轮箱高速轴的转频(理论值8.75 Hz)及其倍频。通过对信号的幅值谱和包络谱分析可见，ICA算法得到的分离信号故障特征不够明显。

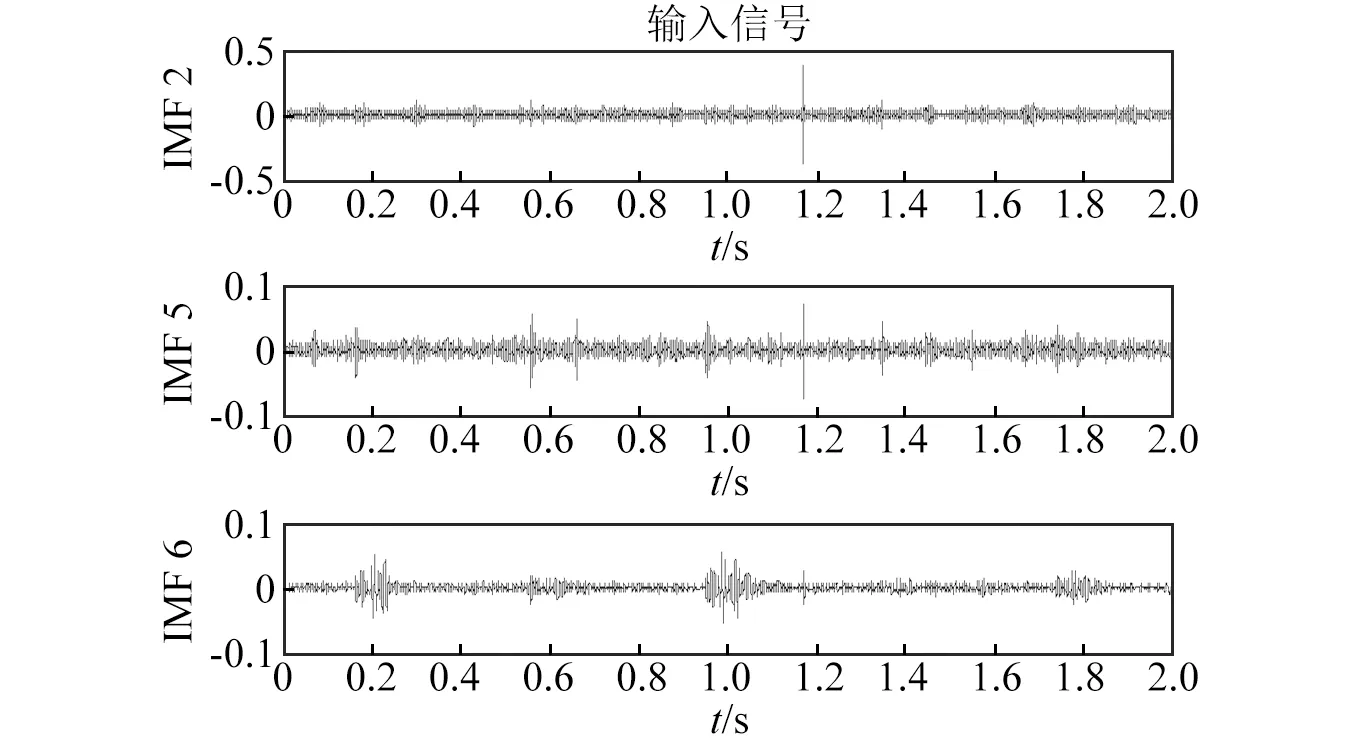
图17 选取的IMF分量Fig.17 The selected IMF components

图18 ICA分离信号的幅值谱Fig.18 Amplitude spectrum of isolated signals by ICA

图19 ICA分离信号的包络谱Fig.19 Envelope spectrum of isolated signals by ICA

将IMF2，IMF5和IMF6输入CICA算法，根据故障齿轮啮合频率及轴承内圈故障特征频率建立参考信号如图20(a)和图20(c)所示，利用CICA算法提取出相应的故障信号如图20(b)和图20(d)所示。对提取信号进行Hilbert包络分析，得到的包络谱分别如图21和图22所示。从图21可知，轴承内圈故障频率(理论值13.78 Hz)，且与图16中重构信号Hilbert包络方法相比较，平行齿轮箱高速轴转频(理论值8.75 Hz)及其倍频幅值明显减小，突出了轴承内圈故障特征。从图22可知，故障齿轮所在的中间轴转频(理论值2.53 Hz)及其倍频成分，与图19的ICA算法包络结果相比，齿轮故障的特征提取效果十分显著。进一步对分离出的齿轮故障信号做幅值谱分析，如图23所示。从图23可知，故障齿轮的啮合频率(理论值91.35 Hz)及其两侧被转频2.53 Hz调制的边频，对比图18中ICA分离信号的幅值谱，可见CICA算法可更好地实现齿轮箱混合故障的分离，突出了齿轮及轴承内圈的故障特征，效果明显。

图20 参考信号及分离出的故障信号时域波形Fig.20 Reference signal and time-domain waveform of isolated fault signal

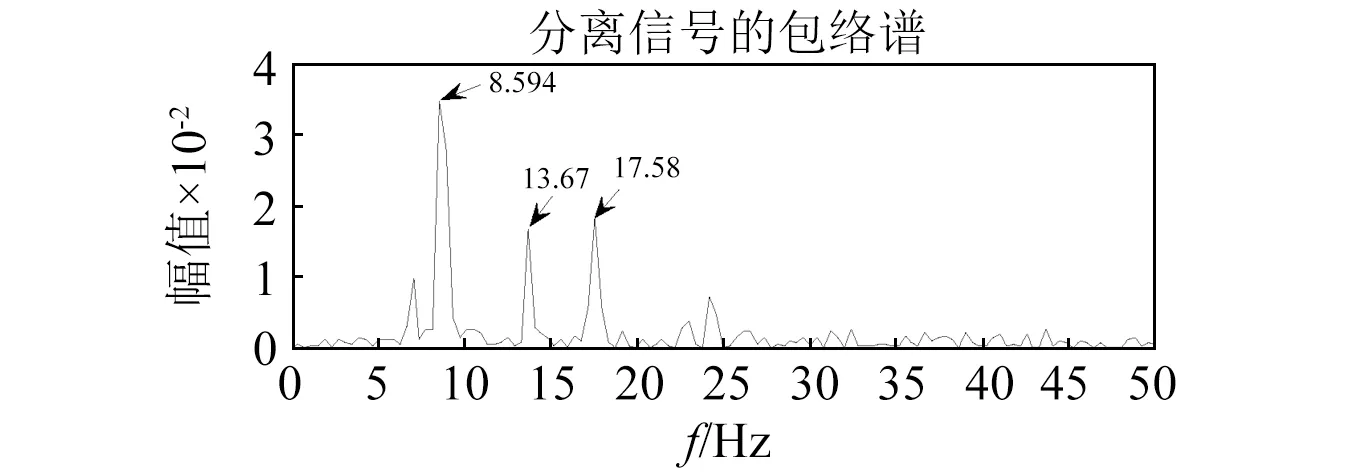
图21 CICA分离出的轴承内圈故障信号包络谱Fig.21 Envelope spectrum of isolated bearing inner ring fault signal by CICA

图22 CICA分离出的齿轮故障信号包络谱Fig.22 Envelope spectrum of isolated gear fault signal by CICA

图23 CICA分离出的齿轮故障信号幅值谱Fig.23 Amplitude spectrum of isolated gear fault signal by CICA

5 结 论

本文针对齿轮箱混合故障特征提取以及盲源分离中的单观测通道欠定问题，结合EMD与盲源分离各自优势，提出基于EMD与CICA结合的混合故障单通道盲源分离方法。采用EMD方法对单通道信号进行预处理，基于白噪声统计特性和峭度值结合方法选取有效的IMF分量，达到了降噪及单通道扩展的目的。将选取的IMF分量输入到CICA算法，依据齿轮及轴承的故障信息建立参考信号，将特定的故障信号分离出来。通过用本文方法对仿真信号与实测齿轮箱混合故障信号进行分离，验证了该方法的可行性和有效性，为混合故障诊断技术提供了新方法。