在线自适应神经网络算法及参数鲁棒性分析

王 涛，翟绪恒，孟丽岩

(1.中国地震局 工程力学研究所 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080；2.黑龙江科技大学 建筑工程学院，哈尔滨 150022；3.同济大学 土木工程防灾国家重点实验室，上海 200092)

混合试验方法是一种将物理试验与数值模拟相结合来检验整体结构动力反应的试验手段。为了提高混合试验中数值子结构模型精度，研究者们提出了基于模型更新的混合试验方法[1-2],即在混合试验过程中利用物理子结构试验数据在线识别数值模型参数[3-4]或在线预测数值子结构恢复力[5-6]。在线模型参数识别算法需要事先假定系统数值模型，然而，算法假定的模型与结构真实滞回关系之间必然会存在模型误差，这将大大降低算法参数识别精度和鲁棒性。

BP神经网络等智能算法不需要事先假定数值模型，可直接利用试验数据在线预测结构或构件恢复力，为解决复杂系统在线模型更新提供了另一种途径。Yang等首先在结构混合试验中，基于试验子结构观测数据采用变神经元节点的神经网络算法在线预测滞回结构的恢复力模型，然后采用训练好的BP神经网络在线预测数值子结构的恢复力。研究表明，该方法能够提高数值子结构恢复力计算的精确性。Yun等[7]提出五变量的神经网络输入，并根据输入变量在滞回曲线不同位置的正负号初步应用在恢复力识别中。张健[8]在此研究成果上又增加了三个输入变量，并应用在混合试验中预测数值子结构恢复力。传统神经网络算法基本采用离线学习方式，然后利用训练好的网络再进行在线预测应用[9]。这种离线学习并不能满足混合试验中数值子结构恢复力在线预测的要求。王涛等[10]在传统的BP神经网络基础上提出一种在线学习的神经网络算法，并应用于混合试验中来在线预测数值子结构恢复力。然而，BP神经网络本质上属于静态前馈网络，对动态系统进行预测时会出现问题。尤其在利用BP神经网络对非线性结构在线识别时，恢复力预测值会出现预测误差偏差的现象，精度较差，这将大大降低混合试验精度，甚至导致试验失败。同时，神经网络在应用时需要人为事先确定算法相关参数，这些参数对算法性能具有重要影响。因此，如何进一步提高神经网络算法在线预测性能并揭示算法参数对算法性能影响规律是亟需解决的问题。

本文首先在传统BP算法的基础上，通过增加反馈层和修改训练样本和权值与阈值更新方式，提出一种在线自适应神经网络算法。然后，通过两组防屈曲支撑(Buckling-Restrained Brace,BRB)构件拟静力试验数据验证所提算法的恢复力预测精度和计算效率。最后，基于BRB构件试验数据对该网络结构中的输入变量、输入和观测样本、隐含层激活函数等算法参数进行了鲁棒性分析，给出算法应用时参数选择建议。

1 在线自适应神经网络算法

传统BP神经网络一般包括输入层、隐含层和输出层，采用离线学习方式优化网络结构各层权值和阈值来逼近任意非线性模型。然而，将该算法直接应用于在线预测时，会产生以下问题：①传统BP算法采用样本批量训练方式进行离线学习，即需要事先得到全部的训练样本，包括所有的输入样本和观测数据。然而，当训练样本只能是批次获得时，传统BP神经网络算法无法进行在线学习，限制了传统算法在线预测应用。②传统BP算法也可仅利用当前步的训练样本直接进行在线学习和预测。传统算法每一步都要对权值和阈值进行初始化，然后重新开始训练参数。可见，这样的学习方式没有充分利用已有的训练样本信息，同时也大大降低了权值和阈值的收敛速度，增加了算法计算负荷。③传统BP算法在当前步的权值和阈值训练结果并没有对下一步权值和阈值训练产生直接影响。也就是说前后相连步之间的参数不存在递推关系，记忆性能差，因此传统BP算法对于动态系统预测的自适应能力不强。

针对传统BP神经网络算法在线预测方面存在的问题，本文提出了一种在线学习的自适应神经网络算法，算法结构示意如图1所示。包含了输入层、隐含层、反馈层和输出层组成。所提出的算法在传统BP算法基础上进行了以下三方面的改进。

图1 第k步在线自适应神经网络结构图Fig.1 Structure of online adaptive neural network at the k step

(1)训练样本的选取方法

在学习阶段，仅利用当前第k步的系统输入和观测数据集{xk,yk}对神经网络结构中的权值和阈值进行内部迭代训练，当满足性能目标后，得到当前步最优的权值Wk和阈值θk。其中，k为算法预测步数；xk为当前第k步的系统输入样本

xk=[x1kx2k…xik…xnk]T

(1)

yk第k步的系统观测样本为

yk=[y1ky2k…yjk…ymk]T

(2)

式中：n,m为输入样本xk和观测样本yk的向量维度。由于仅利用当前的输入和观测样本，而不是得到的所有样本，因此缩减了矩阵运算维度，大大降低了计算负荷。

(2)权值与阈值更新方式

在学习阶段，每一步的权值Wk与阈值θk都是在前一步网络训练得到的权值Wk-1与阈值θk-1基础上进行修正，使得权值与阈值在计算上具有递推形式，充分利用了上一步的训练结果信息，减少了迭代计算耗时。权值更新表达式为

(3)

式中：ΔWk(·)为第k步权值Wk在前一步Wk-1基础上的增量部分，通过网络内部迭代得到；η为学习率，其取值范围在0～1，本文采用固定学习率，η取值均为0.05；E为误差性能函数。阈值的更新方法同上，这里不详细阐述。

(3)增加反馈层

与传统BP神经网络相比，改进算法在隐含层上又增加了一个反馈层。其目的是加强了层间或层内信息反馈，使得在输入与输出之间存在时间上的后滞，承接隐含层输出的信号并存储之前的系统状态，并在下一个输入信号来临后再次作为隐含层的输入，进行系统的非线性映射，从而增强算法自适应动态学习能力。

由图1可知，增加反馈层后，隐含层输入则会发生改变。以第k步第1层隐含层第s个节点为例，其节点输入为

(4)

隐含层第s个节点的输出为

(5)

综上，本文所提出的在线自适应神经网络算法流程，如图2所示。

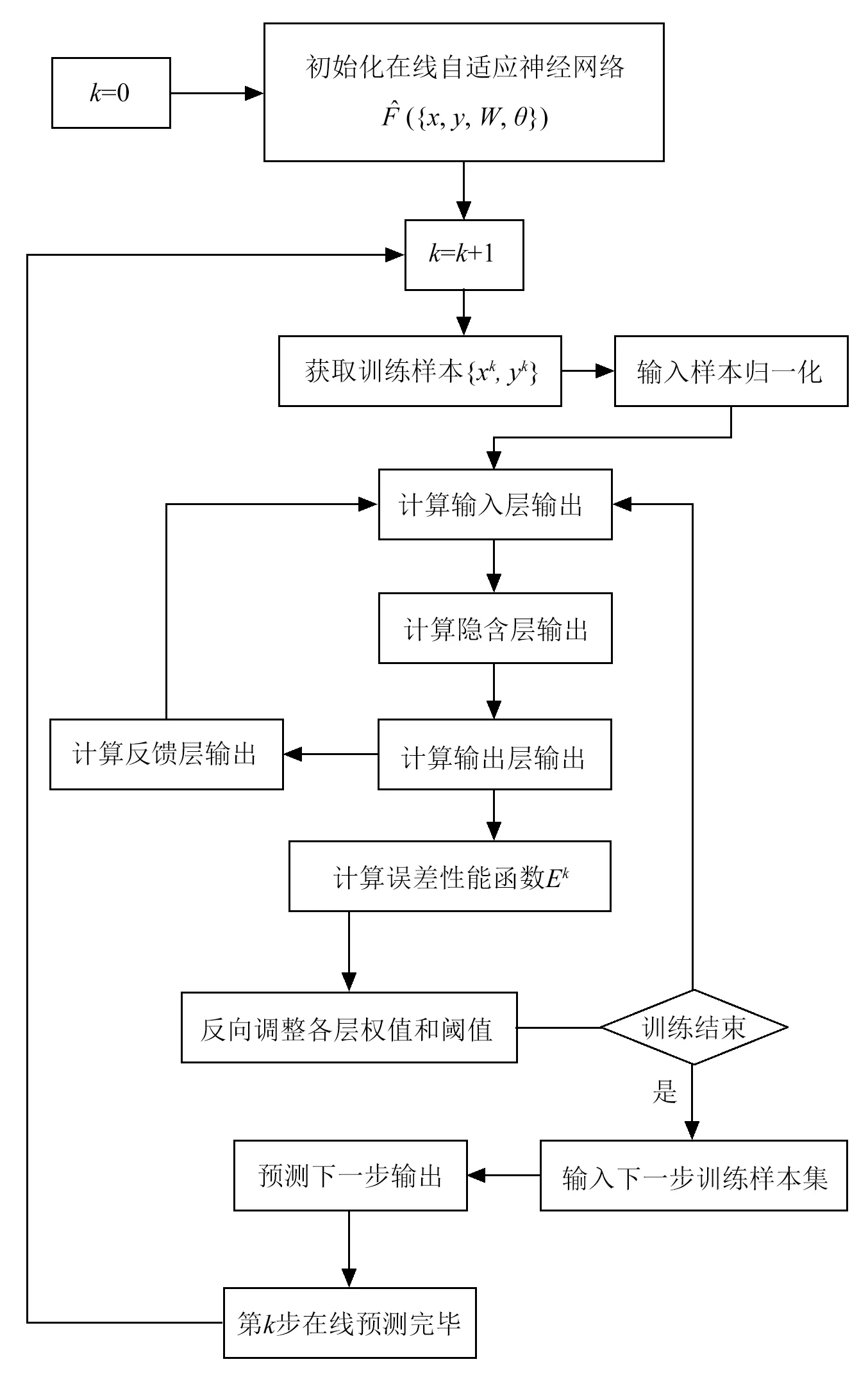
图2 在线自适应神经网络算法流程图Fig.2 Flow diagram of online adaptive neural network

2 算法试验验证

下面通过防屈曲支撑拟静力试验来检验本文所提的在线自适应神经网络算法有效性。采用250 t MTS电液伺服试验机完成两组不同加载路径下的拟静力试验，测得支撑轴向恢复力。防屈曲支撑构件内芯为一字型钢板，截面尺寸为72 mm×13 mm，面积为93.6 mm2，屈服力实测值为309.7 kN；内芯的外部约束采用方钢管，其截面尺寸为70 mm×4.8 mm，屈服力计算值为1 327 kN，约束比为4.28。

为了能通过试验来验证所提出在线神经网络算法性能的有效性，采用以下方案：

(1)首先对同一根BRB构件在两组不同加载路径下的进行拟静力试验，加载步数均为3 000步，试验测得的两组BRB构件轴向滞回曲线，如图3所示。两组试验数据均为同一根BRB构件在两组不同加载路径下的输入和输出。利用一组BRB构件试验的位移和恢复力在线训练神经网络模型，以近似反映BRB构件受力特性，从而利用网络模型在线预测在其它加载路径下BRR构件的恢复力。与第二组BRB构件加载试验相比，第一组试验中BRB构件的加载位移幅度明显更大，即在相同的试验加载步中，第一组试验BRB会首先进入非线性受力状态。为了更好地近似BRB构件的非线性受力性能，选择第一组BRB构件试验的位移与恢复力数据集对神经网络进行训练。

(2)采用两组BRB构件试验数据验证在线自适应神经网络算法有效性，其验证方法示意如图4所示。其中，传统BP神经网络和在线自适应神经网络在当前步学习时，均利用当前步及之前的所有样本集对网络进行训练，然后将第二组支撑试验当前步的输入样本输入到训练好的网络中，从而输出第二组试验支撑在当前步的恢复力预测值。接下来再利用两组试验下一步的数据，进行在线学习，并在线预测第二组支撑在下一步的恢复力，如此循环往复，直至用完所有试验数据而结束。

图3 两组BRB试验滞回曲线Fig.3 Hysteresis curves of two groups of BRB tests

图4 BRB恢复力在线预测示意图Fig.4 Schematic diagram of online prediction of BRB restoring forces

(3)最后将两种神经网络得到的第二组BRB构件恢复力预测值与第二组支撑恢复力试验测量值进行比较，以检验算法预测精度。

采用这种验证方法主要考虑以下两个方面：①与采用单纯的混合试验数值仿真相比，该方案可以在考虑真实BRB构件的力学性能的条件下，检验算法对不同加载路径下试验构件恢复力预测效果。②与进行真实结构混合试验相比，该方案可以在比较经济、安全情况下验证改进算法在线学习及在线预测性能，同时也更为方便对算法参数进行鲁棒性分析。

为了比较改进神经网络算法性能，两种算法采用相同的网络拓扑结构，隐含层节点个数均设为20个，学习率均设定为0.05，训练迭代次数限值设为100次，输入向量采用八变量，分别为：uk,Rk-1uk-1，Rk-1sign(Δuk),uk-1，Rk-1,ut,Rt和ek-1。其中：下标k为试验加载步数；uk为结构层间位移；Rk-1为结构恢复力；ut和ft分别为在滞回环转折点处的位移和恢复力；ek-1为滞回系统第k-1步的耗能，即ek-1=(Rk-1+Rk-2)(uk-1-uk-2)/2；sign(Δuk)为第k步位移增量的符号函数。

为了定量分析试验预测精度，文中选用量纲1的误差指标：相对均方根误差(Root Mean Square Deviation，RMSD)，第k步恢复力预测值RMSDk的表达式为

(6)

第二组BRB滞回曲线的试验测量及预测结果对比如图5所示，图中“Exact”为试验测量值；“BPNN(Back Propagation Neural Network)”为传统离线BP神经网络预测值；“ANN(Adaptive Neural Network)”为自适应神经网络预测值。由图5可知，在线自适应网络算法预测结果与试验结果吻合较好，而传统BP算法的预测结果与试验结果有较大偏差，说明在线自适应算法有较好的预测精度和自适应性。图6给出了两种神经网络算法恢复力预测值相对均方根误差对比，从图6可知,在线自适应算法误差在整体上明显小于传统BP算法，在最终试验结束的第3 000步时，两者的RMSD分别为0.017 2和0.115 94，相对于传统BP算法，在线自适应算法的误差降低了85.16%。

图5 滞回曲线对比Fig.5 Comparison of hysteresis curves

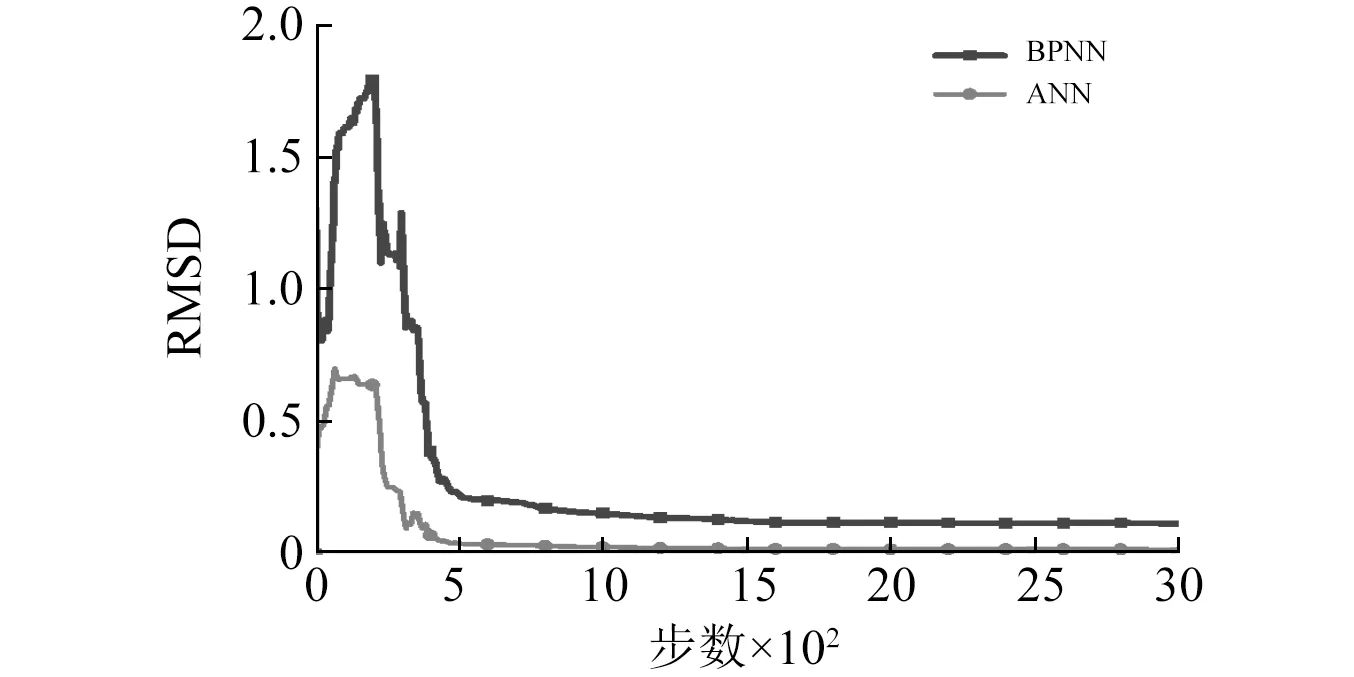
图6 恢复力在线预测精度对比Fig.6 Comparison of online prediction accuracy

为了验证在线自适应神经网络算法的计算效率，在线自适应算法和传统BP算法在全部3 000步中的平均单步耗时为0.20 s和0.43 s。相对传统BP网络算法，在线神经网络算法的计算用时缩短了53.48%。这主要有两方面的原因：①传统算法在每一步上需要利用从开始到当前步的所有样本数据进行训练，而在线自适应算法仅采用了当前步的数据，这样就会大大缩减了运算负荷；②在线自适应网络算法每次进行样本训练时权值与阈值都是在上一步的权值和阈值基础上进行调整的，具有递推性质，不仅充分利用前一步的训练得到的有效信息，避免了网络重新开始训练的步骤，这样就显著减少了训练所需要的用时，从而提高了计算效率。

3 在线自适应神经网络算法鲁棒性分析

神经网络系统是一个非常复杂的算法结构，需要事情确定网络结构和诸多参数，包括：输入变量以及样本集的选择、隐含层的层数以及节点个数设定、激活函数的选取等，这些因素都会直接或间接的影响自适应神经网络算法性能。因此，对算法进行参数鲁棒性是非常必要的。下面仍以第“2”节中的两组BRB构件试验数据分别作为训练样本和预测模型，分析算法参数对预测精度的影响规律。

3.1 输入变量的选择

神经网络输入变量选择对建立高精度的网络结构具有直接关系，从而会影响算法预测精度。当输入变量选择越合理，则越能体现模型非线性的特点。结构滞回特性是具有较强的非线性，结构系统输入位移与输出恢复力并不是一一对应的映射关系。为了能够更好地抓住结构恢复力模型的滞回特性，目前已有三种输入变量形式，即三变量、五变量和八变量，如表1所示。三变量最为简单，分别为uk，Rk-1uk-1和Rk-1sign(Δuk)，其中u为位移，R为恢复力，k为当前步。五变量是在三变量的基础上增加了上一步的位移和恢复力uk-1和Rk-1。张健为了进一步的刻画滞回环的强非线性，在五变量输入的基础上又加入了三个输入变量，即转折点处的位移ut、恢复力Rt及上一步的耗能ek-1，其中，ek-1=(Rk-1+Rk-2)(uk-1-uk-2)/2，从而最终形成了八变量输入形式。

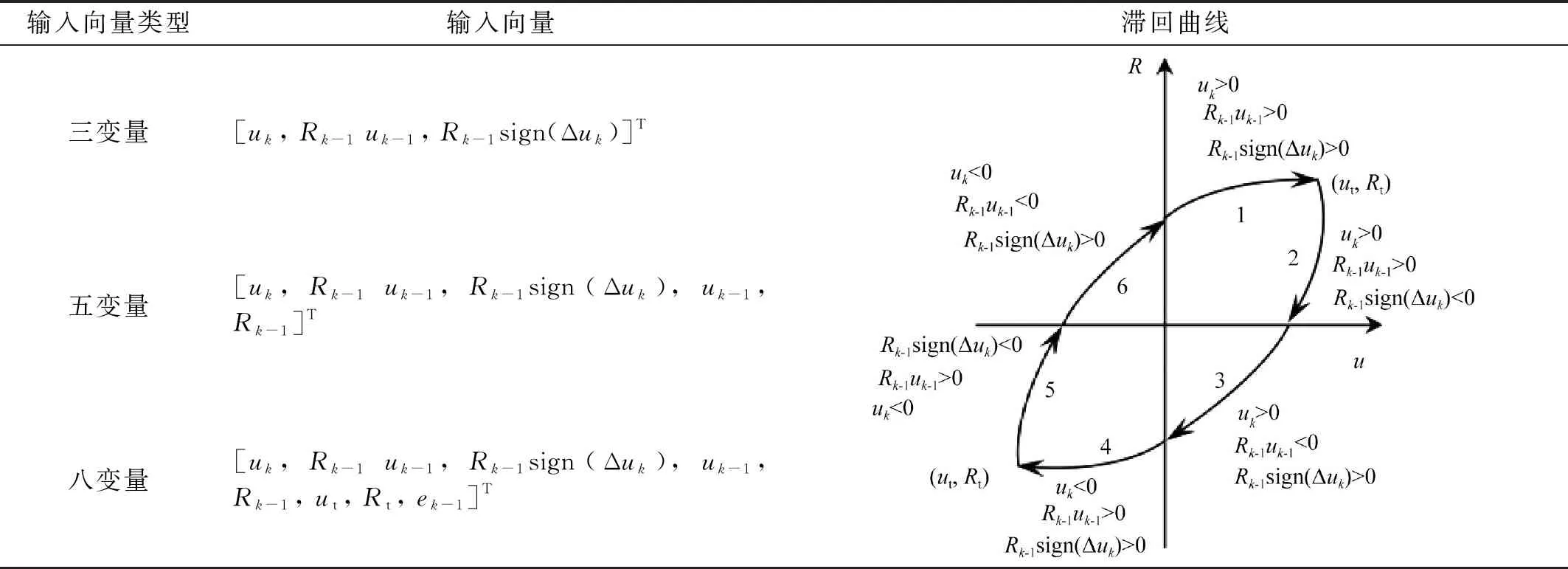
表1 输入变量与滞回曲线的关系Tab.1 Relationship between the input vector and the hysteresis curve

下面分别采用三变量、五变量和八变量的输入向量，分析输入变量对在线自适应神经网络算法预测性能影响。三者均采用当前步以及之前所有步的试验加载数据作为训练样本。采用单层隐含层的拓扑结构，其中隐含层激活函数为tansig函数，输出为结构恢复力。三输入变量、五输入变量、八输入变量的条件下得到的第二组BRB构件恢复力预测值所对应的滞回曲线对比如图7所示。

由图7可知，采用三变量输入时的恢复力预测效果最差，其滞回曲线与试验真实值差别较大；而五变量和八变量输入时预测得到的滞回曲线与试验曲线基本吻合，恢复力预测精度有了很大提高。图8给出了恢复力预测值相对均方根误差对比。在计算到最终的第3 000步时，采用三变量输入时的恢复力预测均方根偏差RMSD达到了约0.202，在三者之中累积误差最大；采用五变量输入时的累积误差RMSD为0.017 2，与三变量相比，精度提高约91.48%；与五变量输入相比，八变量输入对滞回特性的描述更加细致，然而算法预测精度没有提高，反而会下降。

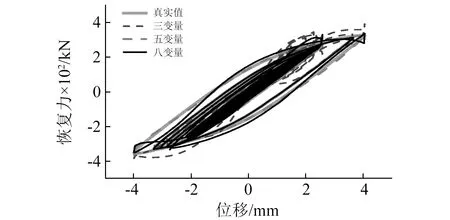
图7 输入向量对滞回曲线预测影响Fig.7 Prediction of hysteresis curves with different input vectors

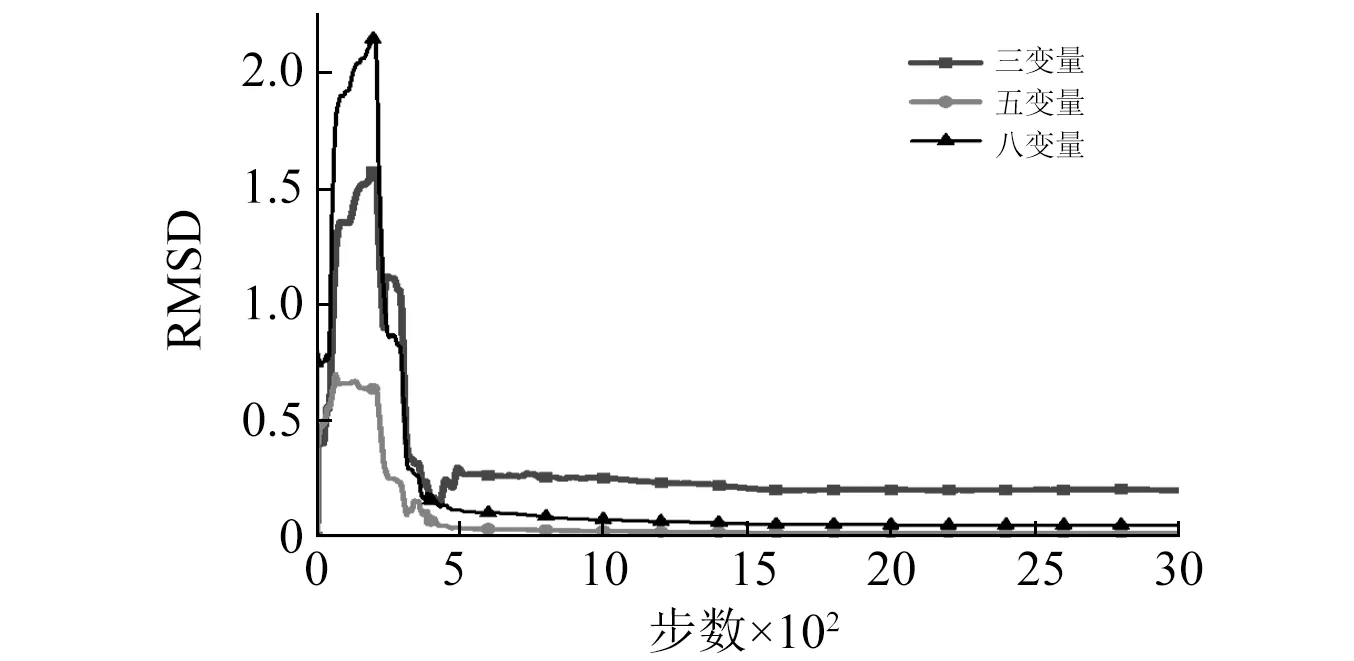
图8 不同输入向量下恢复力预测精度对比Fig.8 Comparison of prediction accuracy of restoring forces with different input vectors

采用三输入变量、五输入变量、八输入变量的三种算法的平均单步计算耗时间分别为0.31 s，0.14 s和0.21 s。可见，采用三变量与八变量的神经网络算法预测的耗时明显高于五变量算法用时。三个输入变量对滞回环的非线性特点描述不够不充分，相对比较粗糙，导致神经网络系统很难建立三个输入变量与输出层的精确映射关系，因此需要增加权值和阈值的训练迭代次数，计算耗时也会随之增大。同时，当采用输入变量过多时，网络结构变得复杂，矩阵运算的维度变大，也更容易造成数据冗余，增加了过学习的可能性，从而导致训练耗时增大。

由以上分析可知，输入变量过少会导致算法预测精度和计算效率降低，输入变量过多，算法预测精度会有明显提高，但同时会增加计算耗时。应用在线自适应神经网络算法进行BRB构件恢复力在线预测时，采用五个输入变量在预测精度和计算效率上效果上都相对更好。

3.2 训练样本数量的选择

在混合试验中，由于试验加载是在线闭环进行，神经网络预测与物理试验加载过程需要同时进行，因此要求在线预测不仅要有较好的鲁棒性，也要有较高的预测精度和计算效率。在确定了在线自适应神经网络算法输入变量后，还要确定在当前步进行训练时所采用的样本数量。训练样本数量将会对算法应能产生直接的影响，下面分别讨论四种样本选取方案，分析样本数量对算法预测效果的影响规律。在下面的对比分析中，所有算法的输入变量始终采用五变量，只是在学习阶段样本数量选取不同。

(1)情况1——在第k步在线学习时，训练样本为从第1步到当前第k步的所有输入样本和观测数据，即1∶k步样本。

(2)情况2——在第k步在线学习时，训练样本为第k-5步到当前第k步的输入样本和观测数据，即k-5∶k步样本。

(3)情况3——在第k步在线学习时，训练样本为第k-1步到当前第k步的输入样本和观测数据，即k-1∶k步样本。

(4)情况4——在第k步在线学习时，训练样本只选用当前第k步的输入样本和观测数据，即第k步样本。

以上四种情况在每一步中均基于第一组支撑试验数据来进行在线学习训练神经网络，然后利用每一步训练好的网络和第二组支撑试验加载位移在线预测第二组支撑恢复力。四种情况下在线自适应神经网络算法得到的滞回曲线对比如图9所示。由图9可知，随着训练样本数量的增加，算法预测得到的第二组支撑滞回曲线与试验真实值就越接近。情况1与情况2的预测结果与试验结果基本重合，而仅采用当前第k步样本的情况5预测结果与试验真实值偏差最大。

为了能更直观看出四种情况预测效果的差异性，采用RMSD定量评价恢复力预测精度。

图9 训练样本个数对滞回曲线预测影响Fig.9 Prediction of hysteresis curves with different training sample numbers

从图10可知，在全部3 000步的整体预测中，从情况1～情况4的恢复力预测值相对均方根误差依次增加。情况1与情况2在第3 000步时的相对均方根误差分别为0.017 2与0.038 2，预测精度较高；对于情况3和情况4在第3 000步时相对均方根误差分别为0.106 9与0.439 1，可见随着样本个数的减少，在线预测精度明显降低。

在计算耗时方面，四种情况单步计算耗时依次分别为：0.136 3 s，0.118 9 s，0.100 8 s和0.066 s。可见，随着样本数量的增加，计算耗时会不断增加。情况1采用当前步以及之前所有步的试验加载数据，预测精度最高，但同时其计算耗时也最大。随着样本数据的不断增多，系统的计算负荷将迅速增大，计算效率会明显降低。因此，若综合考虑预测精度和计算效率，情况2是一种相对更合理的选择。

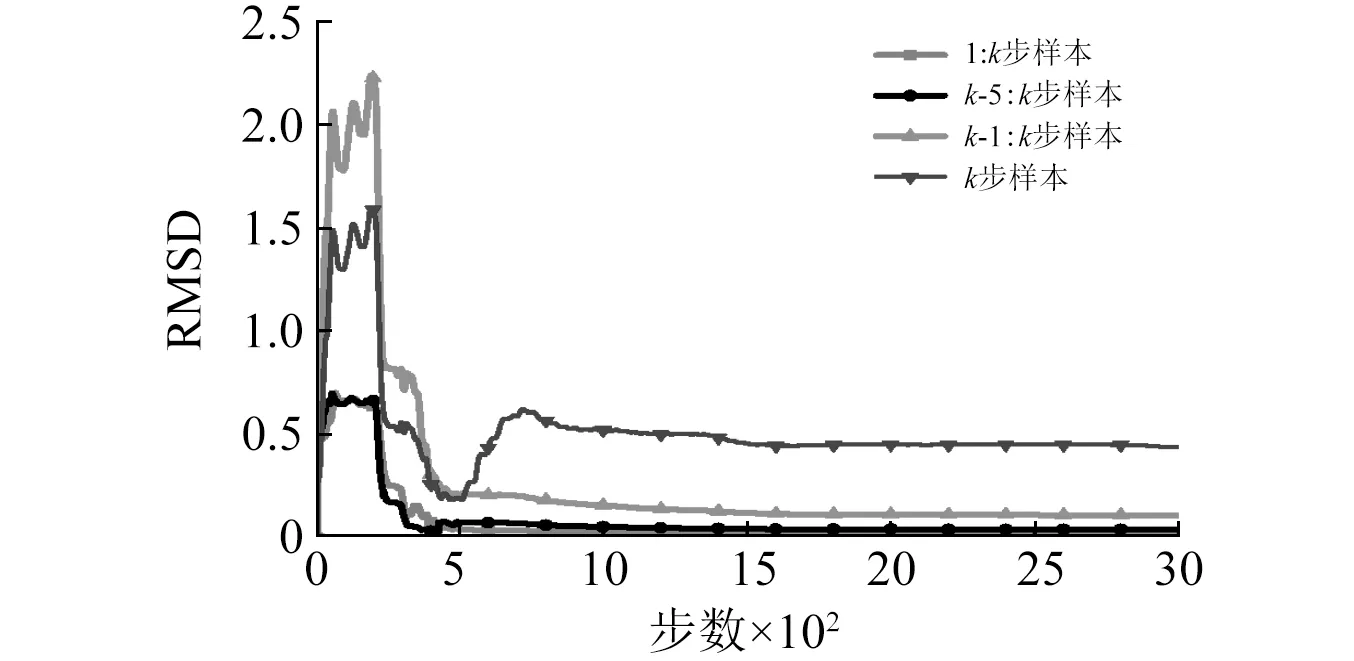
图10 不同样本数量下恢复力预测精度对比Fig.10 Comparisons of prediction accuracy of restoring forces with different training sample numbers

3.3 隐含层激活函数的选择

当确定了输入变量和训练样本后，算法还需要进步确定隐含层的层数和激活函数。在此文中，在线自适应神经网络结构均采用单层隐含层。下面将分别在隐含层中采用两种常见类型的激活函数，即双曲正切函数(tansig)和对数函数(logsig)，分析隐含层激活函数类型对在线自适应算法计算耗时和预测精度的影响规律。其中，输入均采用第“3.1”节中五变量输入，训练样本个数采用第“3.2”节中的情况1，输出层均采用线性激活函数(purelin)，未提的其他参数也均相同。

采用两种隐含层传递函数的在线算法预测得到的第二组支撑滞回曲线，如图11所示。由图可看出，隐含层的激活函数的类型对在线自适应神经网络算法的预测性能影响很敏感。采用对数型激活函数的神经网络预测的效果很差，而采用双曲正切型激活函数的神经网络算法预测得到的滞回曲线与试验真实值基本吻合，此时算法具有较好的预测精度。图12给出了不同隐含层激活函数下恢复力预测精度对比，可以清楚看出双曲正切型激活函数的算法误差要明显小于对数型激活函数的算法误差，两者在第3 000步时的相对均方根误差分别为0.017 2，0.760 2。分析表明：在反馈型神经网络中，双曲正切型激活函数相比于对数型激活函数具有更强的输入与输出映射能力和更高的预测精度。

图11 隐含层激活函数对滞回曲线预测影响Fig.11 Prediction of hysteresis curves with different activation functions in hidden layers

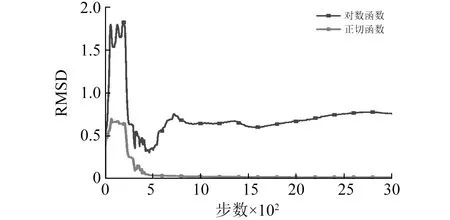
图12 不同隐含层激活函数下恢复力预测精度对比Fig.12 Comparisons of prediction accuracy of restoring forces with different activation functions in hidden layers

4 结 论

本文提出了一种在线自适应动态神经网络算法，通过两组BRB构件拟静力试验数据检验算法对支撑恢复力在线预测效果。研究表明：与传统BP神经网络算法相比，改进算法可以显著提高计算效率和恢复力预测精度。然后又进一步对网络结构中的输入变量、输入和观测样本、隐含层激活函数等算法参数进行了鲁棒性分析，研究表明：与三输入变量和八输入变量相比，五输入变量可以同时取得较高预测精度和计算效率；随着样本数量的增加，预测精度和计算耗时增加，在第k步在线学习时，将第k-5步到当前第k步的输入和观测数据作为训练样本更为合理；隐含层激活函数对算法预测精度影响较大，相比于对数型激活函数，双曲正切型函数在反馈型神经网络中具有更强的输入到输出的映射能力，BRB构件恢复力预测精度更高。