一种圆柱壳类声子晶体振动带隙及振动特性研究

罗金雨，姚凌云，江国期，吴 飞

(西南大学 工程技术学院，重庆 400715)

当前，声子晶体广泛用于振动波的控制，这一领域的形成起源于面向电子波控制的光子晶体概念[1]。声子晶体是两种或两种以上弹性介质组成的具有弹性波带隙的周期复合性材料[2]。当弹性波在声子晶体中传播时，由于散射体的周期性分布，将会禁止某些频率的波传播从而形成带隙。在过去的二十年间，由于声子晶体这一特有物理性质，弹性波在声子晶体中的传播得到了广泛的关注和研究[3-7]。研究表明声子晶体的带隙形成机理可分为布拉格散射(Bragg Scattering)机理和局域共振(Locally Resonant)机理[8]。布拉格带隙的调控依赖于复合介质的材料参数(密度和弹性常数等)和结构参数(晶胞形状、排列方式和填充比)[9]。局域共振带隙与空间排列基本无关，而带隙宽度与材料参数密切相关[10-11]。布拉格声子晶体获得的带隙频率比较高，但是带隙内的衰减比较大。局域共振声子晶体获得的带隙频率比较低，但是由于类Fano现象[12]影响，因此，带隙内的衰减较小。

声子晶体的带隙特性，对于减振降噪技术具有广泛的应用前景。目前对于声子晶体在减振降噪方面的应用，已经做了大量的研究与发展[13-17]。在工程中，最常见的基本结构单元为梁、板和壳结构，因此研究人员对于声子晶体的在工程中的应用也集中与对这三类结构的研究。在梁的振动控制研究中，温激鸿等[18]通过将声子晶体中的周期结构思想引入到梁中，设计构造了一种具有振动带隙的细直梁。Wang等[19]研究了一种局域共振弯曲梁的频散曲线。在板的振动控制研究中，郁殿龙等[20]研究了二维声子晶体薄板的振动带隙,将声子晶体应用到了板结构中。Song等[21]分析和加强了板的弯曲波带隙。

相比于梁和板结构，圆柱壳在工程应用中具有不同之处，具有更广泛的应用。圆柱壳是各种飞机，轮船，火箭和精密仪器的基本结构单元，被广泛应用与化工，航空航天，国防等领域。因此研究圆柱壳的减振特性意义重大，且具有巨大的应用前景。目前研究人员通过分析或数值计算等方法已经研究了波在圆柱结构中的传播[22-23]。由于波在弯曲板和圆柱中传播的复杂性，许多对于弯曲板和圆柱中波的传播研究都使用了简化假设和近似理论。Pany等[24]通过有限元法(Finite Element Method,FEM)研究了轴向波在周期弯曲板中的传播。Manconi等[25]通过有限元法研究了波在圆柱和弯曲板中的传播特性。Nateghi等[26]提出了一种局域共振型圆柱壳，利用有限元法对该模型进行了研究，获得了不同方向的弯曲波频散曲线并讨论了圆柱壳半径对带隙的影响。谢宇晗等[27]通过将吸振器分布在圆柱壳上，使圆柱壳具有了减振降噪效果。

现如今，基于布拉格散射机理的声子晶体类圆柱壳还没有被研究和应用。基于此，作者提出了一种布拉格声子晶体类圆柱壳模型，利用圆柱壳结构动力学理论和Bloch周期条件，建立其结构有限元模型，并计算其能带结构。通过能带结构分析，给出了圆柱壳类声子晶体的能带和带隙的特点。通过对比同种材料参数和同种结构参数的板和壳的能带图，发现环频率会影响壳的第二能带曲线。为进一步的验证环频率对壳的第二能带曲线的影响，本文还给出了单一材料圆柱壳的能带图，得到的环频率与公式计算的环频率基本一致。最后，对提出的模型的振动传递进行了研究，证实了圆柱壳类声子晶体带隙的正确性。同时将带隙外与带隙内的位移场分布进行了对比，可以更加直观的看出该模型的减振效果。基于布拉格散射机理的圆柱壳类声子晶体的振动带隙研究为圆柱类结构隔振降噪方面的应用研究提供了一种新的思路和途径，具有良好的应用前景。

1 周期性结构的圆柱壳模型

1.1 简单模型

为了更好的描述如图1所示的周期结构圆柱壳，本节将笛卡尔坐标转换为圆柱坐标，如图2(a)所示。此时二维波传播的波矢在圆柱坐标中的表示如图2(b)所示。

图1 周期结构圆柱壳及相应的晶胞(边长为0.02 m，圆半径为0.008 m)Fig.1 The periodic shell and corresponding crystal cell (The side length is 0.02 m and the radius of the circle is 0.008 m)

图2 坐标变换及二维波矢的表示Fig.2 Coordinate conversion &representation of wavenumber vector

此时波矢k可以表示为

(1)

在对壳体进行分析时，更习惯使用环向坐标s，轴坐标y和指向圆心的坐标z，如图2(a)所示，即有

Rθ→s,z→y,r→z

(2)

相应的位移为

Uθ→U,Uz→V,Ur→W

(3)

1.2 周期结构圆柱壳结构波传播理论

弹性波在均匀，连续，线性的介质中传播时，传播方程为

(4)

式中：ui=(r,t)为弹性位移场的一个分量；ρ为密度，r=(s,y,z)；σ为应力张量，可以表示成

σij=λtr(ε)δij+2μεij,ij=s,y,z

(5)

式中：tr(ε)为相应应变张量；δij为克罗内克符号；λ和μ为Lamé常数，可用弹性模量E和泊松比ν表示，如式(6)所示

(6)

εij为应变张量具体可用位移场表示为

(7)

根据Bloch-Floquet定理[28]有

u(r,f)=U(r,k,f)ek·r

(8)

2 能带数值分析

目前有很多方法来计算周期结构的能带，本文采取了有限元法(FEM)即利用有限元软件COMSOL Multiphysics来计算周期圆柱壳结构的能带图。有限元法适合于包含有多种材料的声子晶体能带计算和振动分析。

本文利用COMSOL软件建立有限元模型，然后选择固体力学物理场的中的特征频率模块进行计算获得能带图。在COMSOL建立如图1所示的晶胞模型，如图3所示。

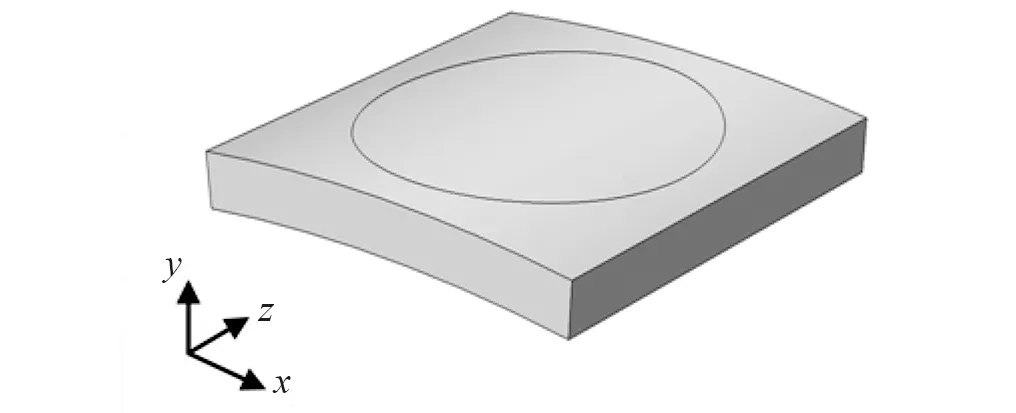
图3 晶胞模型(边长为0.02 m，圆半径为0.008 m)Fig.3 The crystal cell model (The side length is 0.02 m and the radius of the circle is 0.008 m)

对于圆柱壳晶胞模型，COMSOL软件中采用笛卡尔坐标，而圆周方向波矢ks为环向波矢，因此在COMSOL软件中设置圆柱壳周期性条件时，需将ks分解到x和y方向。故本计算中设置Floquet周期k矢量在x，y，z分别为kscos(a/R)π/a，kssin(a/R)π/a，kyπ/a，而对周期结构板的x，y，z分别设置为kxπ/a，0，kzπ/a。其中，a和R分别为晶胞边长和圆柱壳半径。为了保证结果满足有限元法的收敛性要求，本研究在COMSOL软件中将模型划分为7 330个四面体单元组成的网格，其自由度数为35 868。

利用COMSOL软件实际上是解决以下离散系统的二次特征问题

k2A(φ)+kB(φ)+(C-ω2D)=0

(9)

式中：A(φ),B(φ),C和D是基于式(1)、式(4)和式(8)得到的矩阵；A(φ),B(φ)分别为称矩阵和非对称矩阵；C和D分别为结构刚度矩阵和质量矩阵。

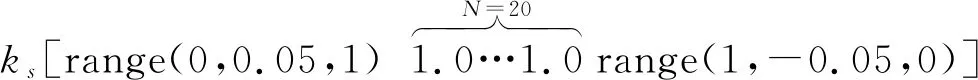
图4 第一布里渊区Fig.4 The irreducible region of the Brillouin zone

利用有限元法即通过COMSOL商业软件计算了半径为0.1 m厚度为0.002 m的周期结构圆柱壳的纵向模态能带图。周期结构圆柱壳如图1所示，基体采用了环氧树脂，散射采用了铅。材料属性参见表1。获得的能带图如图5所示。

表1 材料参数Tab.1 Material parameter

图5 半径为0.1 m的周期结构圆柱壳的能带图Fig.5 The dispersion curve of periodic structure cylindrical shell with a radius of 0.1 m

利用有限元模型进行能带计算，得到如图5所示的能带结构图。图5中带隙1～带隙4表示在该频率内没有振动传播，即振动带隙。如图5所示在0～80 kHz中存在3个完全带隙分别为带隙1、带隙3和带隙4和一个方向带隙即带隙2。第一个完全带隙在29～53 kHz，第二个完全带隙在60～62 kHz，第三个完全带隙在68～73 kHz，表明在这3个频率之间振动被完全禁止传播。方向带隙在54～56 kHz，表明在这个频率之间ΓX方向的振动被禁止传播。

为了评价圆柱壳与板的能带结构的差异，本文还计算了同种材料参数和同种结构参数的周期结构板的能带图。周期结构板如图6所示。板能带图如图7所示。

图6 周期结构板Fig.6 The periodic plate

图7 周期结构板能带图Fig.7 The dispersion curve of periodic structural plates

通过对比板和壳的能带图可以发现，板和壳的纵向模态能带图带隙并没有多大的区别。但是可以观察到板和壳的第二能带有着区别。板的第二能带从0开始，而壳的第二能带从2 095 Hz开始。这个频率可以由圆柱壳的环频率fr的计算公式计算

(10)

由式(10)可知，环频率的大小与所选材料和圆柱壳的半径大小有关，当所计算模型为平板时，可看作半径R为无穷大，此时环频率为0如图7周期结构板的能带图所示。为了进一步的证实环频率对壳的第二能带的影响，文章还给出了环氧树脂为材料的半径为0.1 m的圆柱壳的能带曲线，如图8所示。从图中可以看出第二能带从3 253 Hz开始。由式(10)可知此时fr为3 286.4 Hz，与图中频率相符合。

图8 半径为0.1 m的圆柱壳能带图Fig.8 The dispersion curve of cylindrical shell with a radius of 0.1 m

3 振动传递研究

如图5所示的能带图尽管很好的说明了带隙的频率位置及宽度，但是不能充分的说明周期性圆柱壳的减振特性。为了进一步的说明周期结构圆柱壳的减振特性及验证带隙的正确性，对多个周期(根据隔振要求，一般保证5～10个周期)结构的圆柱壳结构进行了振动传递分析。如图9所示给出了5个周期的振动传递仿真模型，铅柱均匀的插入厚度为2 mm的环氧树脂圆柱壳中，其晶胞大小与图1所示一致，材料参数参见表1。如图5所示周期结构圆柱壳的带隙频率范围集中20～75 kHz，因此采用有限元COMSOL Multiphysics软件划分了44 042个四面体单元形成了266 364个自由度来分析其20～75 kHz的振动传递特性，步长为1 kHz。本文只研究了ΓX方向的振动传递，在T线上施加了沿着如图9浅色箭头所示方向的谐波位移qinc=Qinceiωt，通过COMSOL Multiphysics软件分析计算得到了在右端Homogeneous part部分上的位移响应qres=Qreseiωt。传递系数就可定义为T=20 lg|Qres/Qinc。在Homogeneous part两端施加的完美匹配层(Perfectly Matched Layer,PML)是为了防止边界的散射波，同时模型的两侧运用了周期性边界条件。

图9 振动传递模型Fig.9 The vibration transfer model

根据计算结果获得该周期结构的振动传递函数如图10所示，从图中可以发现，曲线包含4个较大的衰减区域，第一个衰减区域的频率为30～51 kHz,第二个衰减区域的频率在54～56 kHz，第三个衰减区域的频率在60～62.5 kHz，第四个衰减区域频率在67～72 kHz。这与图5所示的带隙基本匹配，但是也存在误差。误差产生的原因是无论是采用有限元法计算带隙还是对振动传递进行仿真，这些都是近似算法，其精度决定于有限元网格的数量和质量，考虑到计算时间等问题只能选择适当的精度来计算。

图10 振动传递Fig.10 The vibration transfer

为了进一步直观的了解圆柱壳类声子晶体的减振特性，图11和图12给出了在带隙外频率点的位移场的分布情况，图13和图14给出了在带隙内的频率点的位移场分布情况。由图11和图12可以明显看出当频率为22 kHz，58 kHz处于带隙之外时，此时振动传递通过了周期结构圆柱壳，此时的周期结构圆柱壳没有任何的减振效果。经过对比可以发现，图13和图14可以明显看出当频率为43 kHz，71 kHz处于带隙内时，此时振动波只向右传递了一个周期，此时振动波的大部分能量都被周期结构反射回去了，因而右边基本没有振幅，振动传递不过去具有良好的减振效果。

图11 22 kHz的位移场分布Fig.11 The displacement field distribution of 22 kHz

图12 58 kHz的位移场分布Fig.12 The displacement field distribution of 58 kHz

图13 43 kHz的位移场分布Fig.13 The displacement field distribution of 43 kHz

图14 71 kHz的位移场分布Fig.14 The displacement field distribution of 71 kHz

4 结 论

本文研究了圆柱壳类声子晶体的振动特性，得到了圆柱壳类声子晶体的能带结构图。对能带图进行研究发现了圆柱壳类声子晶体具有纵向振动带隙。通过将同种材料参数和同种结构参数的壳和板的能带图进行对比，虽发现壳和板的带隙相似，但圆柱壳与板类结构在工程应用中具有不同之处，且圆柱壳结构应用更加广泛，同时发现了壳和板的第二能带具有不同之处，故研究圆柱壳类声子晶体具有重大意义。分析了周期结构圆柱壳的振动传递，发现了在带隙频率内振动传递具有很大的衰减，具有较好的减振特性。通过带隙外和带隙内两个不同的频率所对应的位移场分布，可以更加直观的描述圆柱壳类声子晶体对振动传递的影响。研究表明，圆柱壳类声子晶体具有良好减振效果，这就为圆柱类结构的隔振降噪技术提供了实质性的帮助，同时圆柱壳类结构在工程应用广泛，因此具有振动带隙的周期结构圆柱壳应用前景广阔。