反向转动双机驱动振动筛同步控制
2019-06-13陈长征王远涛
姜 娇,陈长征,薄 磊,舒 鑫,王 仲,王远涛
(1.沈阳工业大学 机械工程学院,沈阳 110870;2.沈阳城市学院,沈阳 110112;3.沈阳鼓风机集团股份有限公司,沈阳 110869;4.辽宁科技学院,辽宁 本溪 117004;5.辽宁电机职业技术学院,辽宁 丹东 118000)
振动筛是一种用于物料颗粒按粒度分级的筛分机械,广泛应用于采矿、冶金、石油、化工、建筑、粮食、垃圾回收等产业。振动筛的种类繁多,包括直线振动筛、圆振动筛、香蕉筛、复频筛、旋振筛、高频振动筛等[1-4]。在实际农业生产中,广泛应用的直线振动筛一般是由双机或双轴反向转动进行驱动。根据振动同步理论,双机或双轴可以实现振动同步运动,取代传统齿轮、链条等强制同步方式,降低了机械的复杂程度、结构简单、制造成本低,节约了能源[5]。虽然自同步直线振动筛有很多优点,但是对于每一台振动筛而言,其振动参数与振动形式往往是固定的,不能方便地进行调节,容易出现物料阻塞现象。针对上述问题,本文以反向转动双机驱动振动筛为研究对象,采用控制同步的方法,方便灵活地改变振动筛的振动形式。
近年来,人们对双机或多机控制同步理论进行了大量研究。Tomizuka等[6]设计自适应前馈控制器,实现了两台直流电机的控制同步。Deng等[7]对永磁同步电机的控制同步进行了研究。Xiao等[8-9]将交叉耦合方法与优化策略相结合,设计了一种广义同步控制器,实现了两台永磁直线电机的同步控制。Zhao等[10]基于相邻交叉耦合控制结构,应用全滑模控制策略,实现了多台感应电动机的速度同步运动。Zhang等[11]研究了多台感应电机的混沌速度控制同步问题。Li等[12]将自适应滑模控制算法引入相邻交叉耦合控制结构实现了多台感应电机的速度追踪和控制同步运动。张承慧等[13]将具有知识表达和自我学习能力的模糊神经网络同步控制器用于四电机的同步控制。但是,在上述研究中,很少涉及振动系统中双机或多机控制同步理论与方法的研究。
本文研究了反向转动双机驱动振动筛控制同步的问题。首先,在考虑感应电动机数学模型的基础上,建立双机驱动振动筛的机电耦合模型。接下来,采用主从控制结构和滑模控制算法,设计主电机的速度控制器和从电机的相位差控制器。对于每台电机,采用矢量控制策略及PI控制算法,实现电机的快速反应。基于Lyapunov稳定性理论及Barbalat引理,分析并验证了控制系统的稳定性。最后,应用Matlab/Simulink仿真分析验证所设计控制器的有效性,并讨论了系统参数的影响。
1 反向转动双机驱动振动筛数学模型
反向转动双机驱动振动筛的模型,如图1所示。筛箱由对称分布的4根弹簧进行支撑,原点o为筛箱质心。两反向转动激振器对称安装于筛箱上提供振动筛所需的激振力。筛箱存在三个方向的运动,分别为x方向的振动、y方向的振动及绕质心的摆动。再加上偏心转子绕自身电机轴的转动,共5个自由度。选择x,y,ψ,φ1和φ2为广义坐标,应用Lagrange方程建立振动筛的运动微分方程[14]
(1)
其中,
式中:l1,2为o~o1,o2的距离,m;r为激振器的旋转半径,m;θ1,2为oo1,oo2与x方向的夹角,°;α为振动方向角,°;m1,2为两激振器的激振质量,kg;mb为筛箱的质量,kg;Jb为筛箱绕质心的转动惯量,kg/m2;le为振动筛的等效转动半径,m;kx,ky,kψ为振动筛三方向弹簧刚度,N/m;fx,fy为振动筛x,y方向阻尼系数,N·s/m;fψ为振动筛ψ方向阻尼系数,N·s/m;J1,2为两激振器的转动惯量,kg/m2;f1,2为两激振器的阻尼系数,N·s/m;Te1,Te2为两激振器的电磁转矩,N/m;TL1,TL2为负载转矩,N/m。

图1 反向转动双机驱动振动筛Fig.1 Vibrating screen driven by two exciters rotating in the opposite direction
双机驱动振动筛是典型的机电耦合系统,对双机驱动振动筛的同步问题进行研究,需要建立感应电动机的数学模型。式(1)的最后两个式子为感应电动机的运动方程。对于电磁系统,感应电动机在d-q两相旋转坐标系下的状态方程为[15]
(2)
式中:d,q为旋转坐标系的d轴和q轴;φdr,φqr为转子磁链,Wb;ids,iqs为定子电流,A;uds,uqs为定子电压,V;Rs,Rr为定子和转子电阻,Ω;Ls,Lr为定子和转子自感系数,H;Lm为定子和转子互感系数,H;Tr为转子时间常数,Tr=Lr/Rr,s;σ为漏磁系数,σ=1-(Lm)2/(LsLr);np为极对数;ωe为同步角速度,rad/s;ω为机械角速度,rad/s。
根据感应电动机的状态方程,获得电磁转矩为
Te=KTiqs
(3)
式中:KT=(3/2)np(Lm/Lr)φdr。
2 反向转动双机驱动振动筛控制器设计
本文采用主从控制结构,滑模控制算法及矢量控制实现两激振器的同步控制,如图2所示。选择电机1为主电机,电机2为从电机。对于主电机1,只需要控制电机角速度等于目标值,对电机的相位不进行控制,利用滑模控制算法设计控制器1。对于从电机2,需要控制其与电机1的相位差等于目标值,同样利用滑模控制算法设计控制器2。而对每个电机电流环的控制采用矢量控制算法,提高电机的响应速度。
将式(3)代入式(1)的最后两式,并整理得
(4)
其中,
a1=-f1/J1,b1=KT1/J1,c1=-1/J1,a2=-f2/J2,b2=KT2/J2,c2=-1/J2,L1=c1TL1,L2=c2TL2。
式中:u1,u2为两电机的转矩电流iqs1,iqs2;L1,L2为有界的不确定量,满足|L1|<δ1,|L2|<δ2;δ1,δ2为正实数。
2.1 主电机控制器设计
(5)
设角速度目标值为ωd,角速度追踪误差为
e1=ω1-ωd
(6)
设计滑模函数s1
(7)
式中:β为正实数;e1(0)为初始速度差,°。
根据式(5)、式(7)可得
(8)
式中:W1=L1;|W|1<δ1。

(9)
为了抵抗干扰的影响,可设计鲁棒控制器为
usw1=1/b1[-ε1sgn(s1)]
(10)
式中:ε1为正实数;sgn(·)为符号函数。
最终,可得滑模控制器为
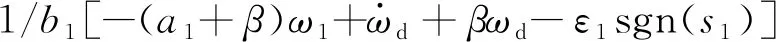
(11)
定义Lyapunov函数为
(12)
显然,V1=0,s1=0和V1>0,s≠0成立。式(12)求导,得
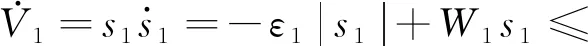
(13)
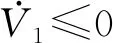
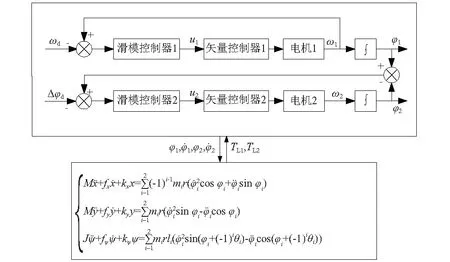
图2 控制系统结构图Fig.2 Framework of the controlled system
2.2 从电机控制器设计
选择两电机的相位差作为状态变量
Δφ=φ1-φ2
(14)
设相位差的目标值为Δφd,相位差的追踪误差为
e2=Δφ-Δφd
(15)
设计滑模函数
(16)
式中:β1,2为正实数。
根据式(4)、式(16),可得

(17)
式中:Δω=ω1-ω2;U=b1u1-b2u2;W2=L1-L2;|W2|=|L1-L2|≤|L1|+|L2|<δ1+δ2。

Ueq=-(a2+β1)Δω-(a1-a2)ω1-
β2(Δφ-Δφd)
(18)
设计鲁棒控制器为
Usw=-ε2sgn(s2)
(19)
式中:ε2为正实数。
由此可得滑模控制器为
U=Ueq+Usw
(20)
定义Lyapunov函数为
(21)
显然,V2≥0。Lyapunov函数的导数为

(22)

最终,从电机的控制器为
u2=1/b2[b1u1+(a2+β1)Δω+(a1-a2)ω1+
β2(Δφ-Δφd)+ε2sgn(s2)]
(23)
为了进一步减弱“抖振”现象,采用饱和函数sat(·)代替符号函数sgn(·),即
sat(si)={1,si>γ
(1/γ)si,|si|≤γ,i=1,2
-1,si<-γ
(24)
式中:γ为正实数。
最后,两电机的滑模控制器分别为
(25)
2.3 稳定性分析

证明:选择Lyapunov函数为
(26)
由式(7),式(16)和式(26),得

(27)
式(27)满足ε1>δ1和ε2>δ1+δ2。定义函数
(28)
对式(28)积分,得
(29)
因为V(0)有界,V(t)有界且非增,可得
(30)
式(28)可整理为
(31)
式(31)对时间求导并整理,得

(32)
由式(32),得
(33)


(34)

3 仿真实例
本节应用Matlab/Simulink仿真验证控制方法的有效性。振动筛和两电机的相关参数分别列于表1和表2。矢量控制结构图见文献[16]。

表1 振动筛参数Tab.1 Parameters of the vibrating system

表2 感应电动机参数Tab.2 Parameters of induction motors
3.1 仿真分析
选择参数m1=m2=4 kg,l1=l2=0.5 m,验证所设计控制器的有效性。目标角速度ωd=95 rad/s,目标相位差Δφd=0°。控制器的相关参数为:β=16,β1=16,β2=64,ε1=788,ε2=1 150,γ=1;矢量控制的PI参数为:kp1=184,ki1=11 474,kp2=223,ki2=7 490。图3为控制同步的仿真结果。如图3(a)所示,目标角速度ωd=95 rad/s,稳态时,两激振器的角速度基本相同,由于振动的影响,二者均在94.6~95.4 rad/s以近似正弦变化。图3(b)为两激振器相位差随时间的变化曲线。可以看出,在起动阶段,两激振器的相位差达到约-130°;在控制器的作用下,在1 s内收敛于Δφ≈0°。通过上述仿真结果可知,两激振器实现了控制同步运动。由于系统本身为典型的机电耦合系统,振动筛箱与电机之间是相互作用,相互影响的。在两激振器未达到零相位差同步运动时,振动筛x-,y- 和ψ-方向的响应变化很大,如图3(c)~图3(e)所示;稳态时,由于两激振器的相位差为0°,筛箱所受外激励方向为y-方向,所以筛箱x-与ψ-方向的响应为0,与计算结果一致。图3(f)为筛箱质心的运动轨迹,由于筛箱作y-方向的直线振动,质心的运动轨迹为直线。显然,应用本文所提出的控制同步方法也可以实现反向回转双机驱动振动筛的直线振动形式。
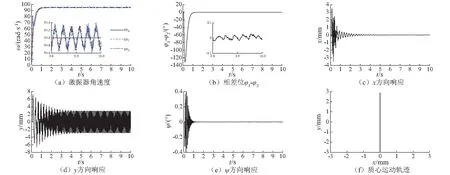
图3 控制同步仿真结果(m1=m2=4 kg,l1=l2=0.5 m,Δφd=0°)Fig.3 Simulation results of controlled synchronization (m1=m2=4 kg,l1=l2=0.5 m,Δφd=0°)
3.2 参数影响
首先,讨论目标转速ωd的变化对控制系统的影响,其他系统参数保持不变,即m1=m2=4 kg,l1=l2=0.5 m,Δφd=0°。图4为控制系统在目标转速发生变化条件下的仿真结果。如图4(a)所示,目标转速ωd在t=5 s时由95 rad/s变为80 rad/s。在目标转速发生变化时,从电机的角速度始终与主电机的角速度保持一致;当系统达到稳态时,两激振器的转速在80 rad/s附近以近似正弦的形式变化。当t=5 s时,两激振器的相位差始终等于0°,见图4(b)。在图4(c)和图4(d)中,由于激振器角速度的变化,造成筛箱x和y方向的响应从稳定状态变为不稳定状态;但是,在3 s内,x和y方向的响应又重新达到稳态。图4(e)为筛箱ψ方向的响应曲线,可以看出:其变化规律与相位差的变化规律是基本一致的。由于仅仅转速发生改变,而两激振器的相位差未发生变化,因此筛箱的运动轨迹不发生变化,仍然为直线,如图4(e)所示。从上述分析可以看出:控制系统对于目标转速的变化具有很强的鲁棒性;同时,采用本文提出控制同步的方法,可以很好地调节振动筛的工作频率。

图4 不同目标转速条件下控制同步仿真结果(m1=m2=4 kg,l1=l2=0.5 m,Δφd=0°)Fig.4 Simulation results of controlled synchronization with desired speed changes (m1=m2=4 kg,l1=l2=0.5 m,Δφd=0°)
图5为Δφd=90°时控制同步的仿真结果。如图5(a)所示,稳态时,两激振器的转速在94.4~96.6 rad/s以近似正弦的形式波动,显然可以说明两激振器实现了同步控制。如图5(b)所示,稳态时,两台电机的相位差在90°附近变化,与目标值之间的差值在0.1°以内,说明在控制器的作用下两激振器实现了相位差为90°的同步运动。由于两激振器相位差的存在,筛箱所受x方向的激振力不恒等于0,造成振动筛在x方向的响应的幅值不等于0,如图5(c)所示;同时,筛箱所受y方向的激振力的幅值与0相位差时相比有所减小,振动筛在y方向的响应的幅值相应的有所减小,如图5(d)所示;此外,振动筛存在轻微地摆动,如图5(e)所示。此时,式(1)的前两式的解可表示为x=Xsin[(φ1+φ2)/2-φx],y=Ysin[(φ1+φ2)/2-φy],依据参数进行计算可知φx≈φy,所以筛箱质心的运动轨迹仍然近似为直线,与图5(f)所示结果是一致的。通过上述结果可知,采用本文所提出的控制同步方法,可以调节振动筛的振动方向角。
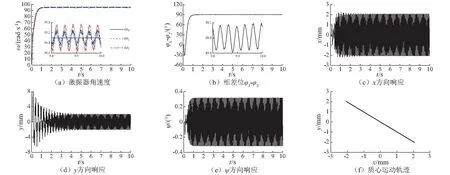
图5 控制同步仿真结果(m1=m2=4 kg,l1=l2=0.5 m,Δφd=90°)Fig.5 Simulation results of controlled synchronization (m1=m2=4 kg,l1=l2=0.5 m,Δφd=90°)
最后,分析不同激振质量对控制同步运动的影响。图6为m1=3 kg,m2=5 kg时控制同步的仿真结果。激振质量的变化,对于控制系统而言,改变了系统的外部干扰量,但是,由图6(a)和图6(b)可知,两激振器实现了控制同步运动,且相位差仍为0°。但是,由于m1≠m2,振动筛的响应为x=X1cos(φ1-φx),y=Y1sin(φ1-φy),ψ=Ψ1sin(φ1-φψ),筛箱存在x,y方向的平动及ψ方向的摆动,且质心运动轨迹为椭圆,与图6(c)~图6(f)所示仿真结果一致。上述结果再次表明,本文所设计控制系统具有很强的鲁棒性;同时说明采用控制同步方法不仅可以实现直线的振动形式,而且可以实现椭圆的振动形式。
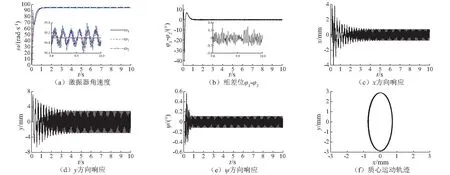
图6 控制同步仿真结果(m1=3 kg,m2=5 kg,l1=l2=0.5 m,Δφd=0°)Fig.6 Simulation results of controlled synchronization (m1=3 kg,m2=5 kg,l1=l2=0.5 m,Δφd=0°)
4 结 论
(1)基于滑模控制算法和矢量控制及主从控制结构,设计了两激振器的转速和相位差控制器,并应用Lyapunov稳定性判据及Barbalat引理,证明了所设计同步控制系统的稳定性。
(2)仿真分析发现:采用本文设计的控制器,可以实现两激振器任意相位差的同步运动,说明了所设计控制系统的有效性。同时,分析了目标转速、目标相位差、激振质量等参数变化对控制同步系统的影响,充分说明了本文所设计同步控制系统具有很好的鲁棒性。
(3)本文所提出控制同步的方法,可以成功地用于反向转动双机驱动振动筛,根据物料筛分情况,通过调节两激振器的相位差、激振质量、转速等参数,可以方便地调节筛箱的振动形式,避免筛孔的堵塞现象,获得理想的筛分效果,提高筛分效率。
