基于波原子变换的三维地震信号盲去噪

何 峰，周亚同，赵翔宇，石超君

(河北工业大学 电子信息工程学院 天津市电子材料与器件重点实验室，天津 300401)

地震信号由震源的振动产生，沿地层传播后被检波器采集接收[1]。在采集过程中地震信号往往含有高斯随机噪声。去噪时噪声水平未知，只能进行盲去噪。目前信号盲去噪算法主要分三类：①噪声估计与非盲去噪结合的去噪[2]；②信号评估与无参非盲去噪[3]；③同时进行噪声估计并去噪[4]。

本文拟采用第一类盲去噪算法，首先对信号进行噪声估计，然后利用噪声标准差作为非盲去噪输入参数。目前噪声估计主要为三类：①基于块算法[5]，将信号规则或非规则分块，再找出强度变换(噪声引起)最小块，此块即标准差最小的块；②基于高通滤波算法[6]，将信号经过高通滤波，再计算含噪信号与滤波后信号的差值，得到噪声标准差。但对复杂纹理信号，此算法有时不准确，会发生过估计；③基于统计算法：Zoran等[7]提出一种基于统计的估计算法，分析DCT(Discrete Cosine Transform)滤波的信号后，发现噪声的存在导致了峰值变化，利用该影响准确估计出噪声标准差。本文所用估计算法为基于块的算法[8]。

常见变换域非盲去噪算法主要有：小波去噪[9]、脊波去噪[10]、轮廓波去噪[11]、曲波去噪[12]等。波原子变换是一种新型的多尺度几何分析工具，相比小波、曲波等，对震荡型纹理型信号具有“最优”稀疏表示，且能同时表征沿振荡与穿过该振荡方向的信息。已有研究学者将其应用于信号去噪领域，如Haddad等[13]将波原子应用至典型纹理型信号(指纹)压缩，表现出波原子优势。Zhang等[14]提出一种波原子结合循环平移的算法，较好地抑制了信号边缘易出现的伪吉布斯现象。杨宁等[15]将波原子应用至叠前地震信号的信噪分离，利用各尺度间系数相关性去噪。这些研究表明波原子对振荡纹理型信号的处理优势。而地震同相轴的排列组合可视作纹理，故波原子变换亦适用于处理地震信号。

本文提出一种基于波原子变换的三维地震信号盲去噪算法，利用噪声估计得到信号的噪声标准差，再对信号进行循环平移并在波原子变换域处理，按不同尺度分层选取阈值并进行修正，然后利用改进阈值函数处理波原子系数，再波原子反变换与反循环平移得到去噪后信号。合成与实际地震信号实验表明，本文算法能够有效去除地震信号噪声。

1 基于块的地震信号噪声估计

针对纹理复杂场景易出现过估计问题，从含噪地震信号中选出不含高频分量的低秩信号块，再从利用主成分分析(Principal Component Analysis，PCA)估计噪声。

1.1 基于PCA的噪声估计

设含噪信号块的生成模型为

yi=zi+ni,i=1,2,…,M

(1)

式中：M为分块数量；zi为无噪信号块；ni为均值为0，方差为σ2的高斯白噪声。将数据方差投影到某个轴，则投影向量的方差为

(2)

式中：u为单位向量；V(uTyi)为zi在u方向的方差。可利用PCA求解，则

(3)

(4)

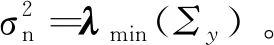
1.2 低秩信号块选择

信号结构的复杂度可利用梯度协方差计算。信号块yi的梯度矩阵为Gyi=[DhyiDvyi]，其中Dh与Dv为水平与垂直导数算子。梯度协方差矩阵为

(5)

式中：T为转置运算符；V为Cyi的特征向量；s1与s2为特征值。协方差矩阵的迹能够反映出信号块的纹理强度。则定义纹理强度ξi为：ξi=trace(Cyi)，其中trace()为求迹运算符。ξi越小，则信号越平滑，纹理越弱。梯度矩阵对噪声极敏感。此时需考虑一种低秩块的极端情况：理想的无噪信号块zf的梯度为0，即Gzf=[DhzfDvzf]=[0 0]，则得yf的梯度矩阵为

Gyf=[Dh(zf+n)Dv(zf+n)]=
[DhnDvn]=Gn

(6)

则含噪块yf的纹理强度为

(7)

为简化问题求解，用Gamma分布来近似ξn分布，其概率密度函数为

(8)

式中：α为形状参数；β为尺度参数。

假设给出的含噪块为理想块(即无噪信号块的梯度为0)，置信区间为：P(0<ξ(n)<τ)=1-δ，其中τ为阈值，δ为显著性水平。若信号块的ξi小于阈值则认为其为弱纹理块(低秩块)。阈值τ可由δ与σn定义

(9)

式中：Gamma-1(δ,α,β)为Gamma反分布;N2为信号块中的像素数量。

1.3 噪声估计迭代过程

选出低秩块就可准确估计噪声标准差。但选择弱纹理块的阈值τ应可变。用迭代来选择需要的块并估计噪声。具体过程如下：

步骤3用τk+1从含噪信号中选出弱纹理块Wk+1；

步骤4然后用Wk+1与τk+1估计噪声标准差；

步骤5重复步骤2～步骤4，直至噪声标准差不变。

2 波原子变换

波原子是一种新型的多尺度几何分析工具[16]，是一种遵循抛物比例尺度关系的二维小波包的变体。对于给定精度，以一个N×N大小的二维信号为例，仅需o(N)波原子系数就可稀疏表示该信号，若要表示相同精度，则需曲波系数o(N3/2)，小波和Gabor系数o(N2)。波原子能以最少的系数最优稀疏表示信号，因此本文选择波原子作为变换基。

2.1 波原子定义

若将波原子表示为wμ(f)，其中μ=(j,m,n)=(j,m1,m2,n1,n2),j,m1,m2,n1,n2∈Z，设(fμ,ωμ)为相空间中任意的一点，且满足

(10)

式中：C1,C2为正数；j,m,n分别为尺度、频率与空间系数；fμ与±ωμ为空间域wμ(f)与频率域wμ(ω)中心。

若wμ(f)满足空域局部条件

|wμ(f)|≤CM2j(1+2j(ω-ωμ))-M

(11)

且满足频域局部条件

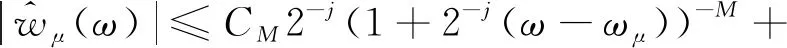
(12)

则称波包{wμ}为波原子。

2.2 波原子构造及系数求解

(13)

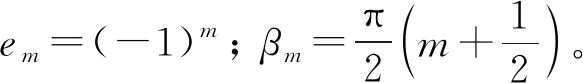
(14)

离散波原子变换的系数为

coeffj,m,n=

(15)

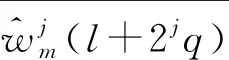
(16)

(17)

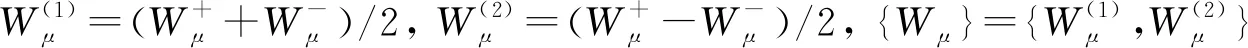
3 基于波原子变换的三维地震信号盲去噪过程

3.1 总体去噪流程

本文基于波原子变换的三维地震信号盲去噪的总体去噪流程为：

步骤1利用噪声估计算法估计信号噪声标准差；

步骤2对地震信号进行循环平移运算；

步骤3循环平移后信号做波原子变换得到系数；

步骤4对变换系数进行阈值选取和修正；

步骤5构造阈值函数，基于该函数对波原子变换系数进行筛选处理；

步骤6对处理后系数进行波原子反变换；

步骤7对反变换结果进行反循环平移，得到当前循环平移的结果；

步骤8重复步骤2～步骤7，至所有循环平移完成；

步骤9对每次循环平移得到的去噪结果求平均值，得到最终的去噪地震信号。

3.2 地震信号循环平移

波原子变换缺乏平移不变性，会导致在边缘或纹理等不连续点临域内产生伪吉布斯现象，造成去噪信号的失真[17]。为了防止该现象，Coifman等[18]提出一种循环平移算法，即将信号做循环平移，然后阈值去噪，再做反循环平移。每次伪吉布斯现象会在不同位置出现。三维地震信号循环平移表达式为

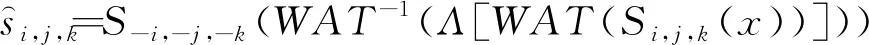
(18)

3.3 阈值选取及修正

记波原子变换系数的阈值为λ，作为波原子去噪算法中的重要参数，会直接影响去噪效果。Donoho等[19]提出一种VisuShrink阈值法

(19)

式中：K为可调参数；σn为噪声标准差；N为波原子系数长度，但该阈值为全局阈值。通常噪声的波原子系数在低尺度时较大，在高尺度时较小，因此阈值参数也应该随尺度的变化而变化，即阈值应与波原子变换尺度成反比关系，但变化范围不宜过大。且全局阈值会导致地震信号细节的丢失，因此本文采用分层阈值

(20)

式中：j为波原子变换的尺度；Nj为第j层波原子变换系数的长度。考虑到地震信号的特点，波原子变换的系数偏大，因此阈值也应相应变大，但不宜过大，因此考虑引入指数函数，且指数参数不宜过大，应为一接近零的值。经由实验发现，随地震信号的含噪量的增大，阈值也应随之稍有增大。因此在多尺度分层阈值选取的基础上，引入噪声参数，提出了随信号含噪量自适应变化的阈值修正

λnew=λ·e1/(m·n·d)

(21)

式中：m为波原子分解最大尺度；n为一常数，本文取n=4；d与噪声大小有关d=2/σn。

3.4 阈值函数构造

硬阈值函数保留了信号的局部特性，但由于其不连续性，导致处理信号时存在一定的波动与振荡。硬阈值函数为

(22)

式中：cλ为阈值函数处理后得到的系数；c为波原子系数；λ为阈值。

软阈值函数在阈值处连续，处理系数时会更平滑，但会损失一部分高频信息，且存在固有的偏差，会使信号模糊。软阈值函数为

(23)

软阈值函数的连续性比硬阈值好很多，但为克服其存在的固有偏差，又提出了软硬阈值折衷算法

(24)

式中：T介于0～1。尽管效果有所改善，但T是固定值，针对不同尺度的系数，很多学者提出了改进算法[20]。考虑到软硬阈值的优缺点，要克服硬阈值函数在阈值点处不连续的缺点，还有解决软阈值函数处理前后存在的固有偏差。因此需找到一种函数，在阈值点处连续，且应为高阶可导的。综合软硬阈值不同特点，本文构造了一种新的阈值函数

(25)

4 实验结果与分析

为验证本文算法对三维地震信号的去噪效果，以合成地震信号为例，验证阈值修正、改进阈值函数与循环平移对传统波原子去噪效果的提升。然后以合成与实际地震信号为例，将小波变换(Wavelet Transform，WT)、双树复小波变换(Dual Tree-Complex Wavelet Transform,CPLX_DT_WT)、曲波变换(Curvelet Transform,CT)以及传统波原子变换(Wave Atoms Transform,WAT)与本文算法对比。采用输入信噪比(SNR_IN)作为输入地震信号的含噪大小衡量指标，以输出信噪比(SNR_OUT)、均方误差(MSE)以及峰值信噪比(PSNR)作为去噪质量评价指标。

4.1 去噪处理过程前后性能对比

本实用采用合成地震信号，并归一化至[0,1]。信号共41×41=1 681道，每道85个采样点。为定量分析去噪效果，分别添加信号最大幅值的5%，10%，15%，20%，25%与30%的噪声。图1为归一化后信号。

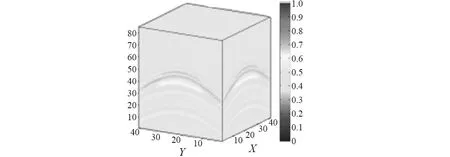
图1 三维合成地震信号Fig.1 3D synthetic seismic signal

表1为各去噪手段处理前后的性能对比，其中“未修正”表示多尺度阈值与硬阈值函数；“阈值修正”表示分层多尺度阈值后进行阈值修正，再硬阈值函数处理系数；“改进阈值函数”表示分层多尺度阈值并进行阈值修正，然后采用改进阈值函数；“循环平移”表示在“改进阈值函数”前对地震信号进行循环平移。其中参数设置为p=0.9，q=10(σ≥25%)或15(σ<25%)。对比指标采用PSNR。

表1 去噪处理过程性能对比Tab.1 Performance comparison of denoising process

从表1中列与列两两对比可知，阈值修正前后PSNR有了一定提升，噪声较小时提升不明显，但随信号含噪量增大，去噪效果提升越明显，表明阈值修正对去噪效果的提升；改进阈值函数比硬阈值函数处理系数能获得更优秀去噪效果；循环平移处理前后去噪效果提升最明显，即使在含噪量仅为5%时，也将PSNR从34.089 3提升至34.769 2。但循环平移会造成运算时间增加。从整体分析可看出，数据从左至右，PSNR从小变大，且随信号含噪量增大，PSNR值也越大。表明阈值修正、改进阈值函数与循环平移处理的有效性。

4.2 合成地震信号去噪

本实验针对合成三维地震信号去噪，所用地震信号同第“4.1”节，添加噪声大小分别为信号最大幅值的5%，10%，15%，20%，25%及30%。对比算法采用全局经验阈值。因为经验阈值往往为能够取得各算法最好去噪效果的阈值。图2为对图1合成地震信号添加噪声后信号。

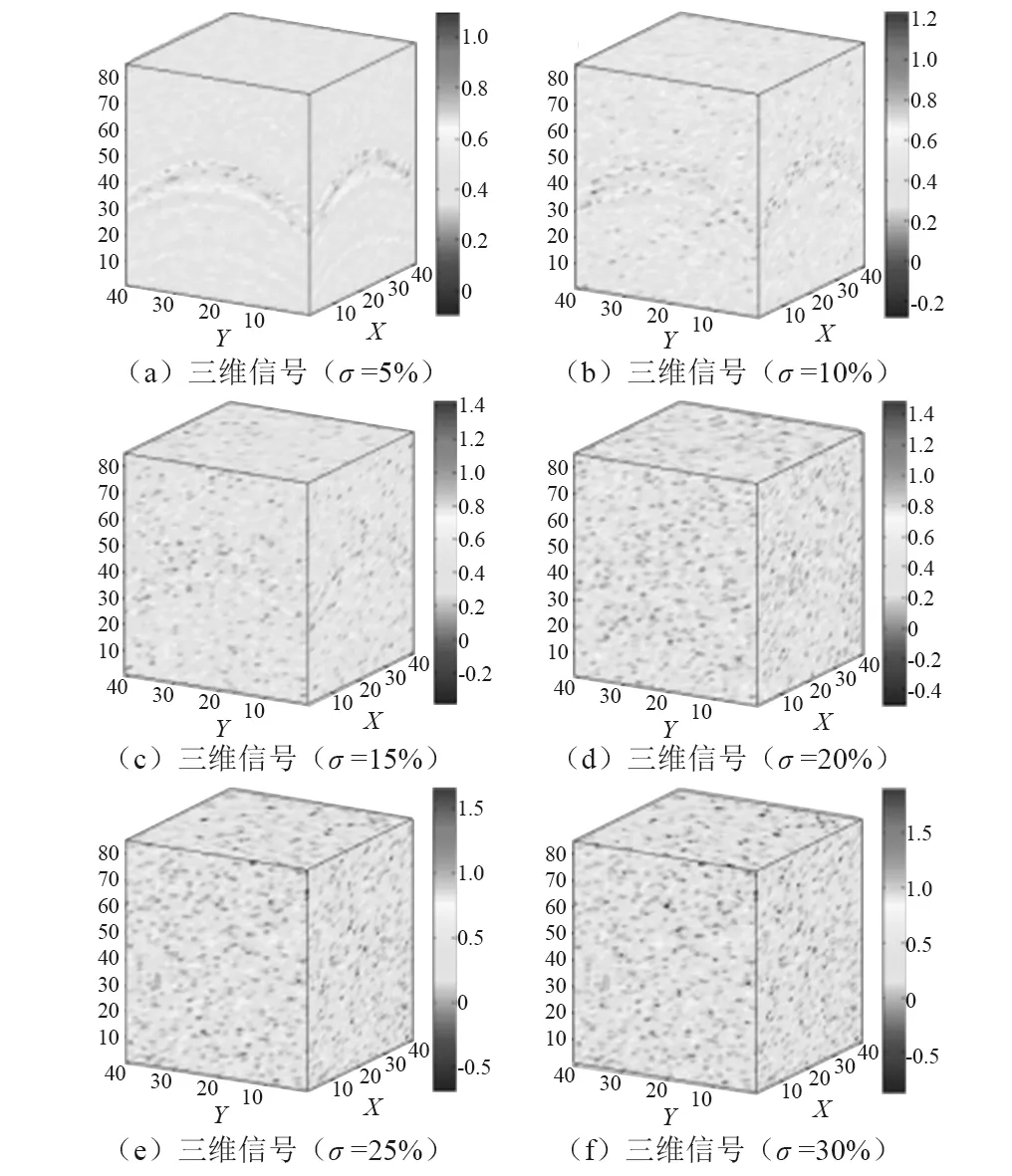
图2 含噪的合成三维地震信号Fig.2 3D synthetic seismic signal with noise

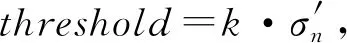
表2 合成地震信号去噪评价指标Tab.2 Denoising evaluation index of synthetic seismic signal

从表2可知，同一噪声水平下，针对各重建算法，由于MSE较小，因此去噪效果差距不明显，但从SNR_OUT与PSNR可以看出，WT去噪质量稍差，而CPLX_DT_WT与CT，WAT的去噪效果优于WT。本文算法在任何噪声水平下均取得最佳的去噪效果，明显优于其他对比算法。图3为添加噪声幅度为5%时，各算法去噪效果图。

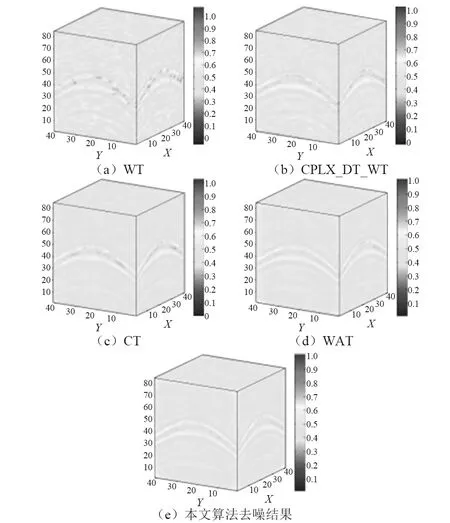
图3 各算法去噪结果Fig.3 Denoising results of each algorithm

从图3去噪结果可知，WT与CPLX_DT_WT的去噪结果图3(a)与图3(b)表面仍稍有较明显的噪声痕迹；CT与WAT的去噪效果如图3(c)与图3(d)，只残余轻微的噪声痕迹；而本文提出的算法，图3(e)可知，本文算法的去噪效果最好，基本将噪声去除。本实验说明，相对其他对比算法，本文算法能以较大优势去除合成地震信号的噪声。

4.3 实际地震信号去噪

本实验信号源自北海F3数据体，F3是北海位于荷兰的一个区块，已采用OpendTect进行了倾角导向滤波。信号范围为In-line：400-527；Cross-line：700-827；Time：480-732。In-line与Cross-line方向空间采样率为1，时间采样率为4 ms，故信号大小为128×128×64。将信号归一化至[0，1]。图4(a)、图4(b)分别为原始实际三维地震信号的三维与横切片图。图5为添加信号后的信号。

图4 三维实际地震信号Fig.4 3D real seismic signal

图5 含噪的实际地震信号Fig.5 Real seismic signal with noise

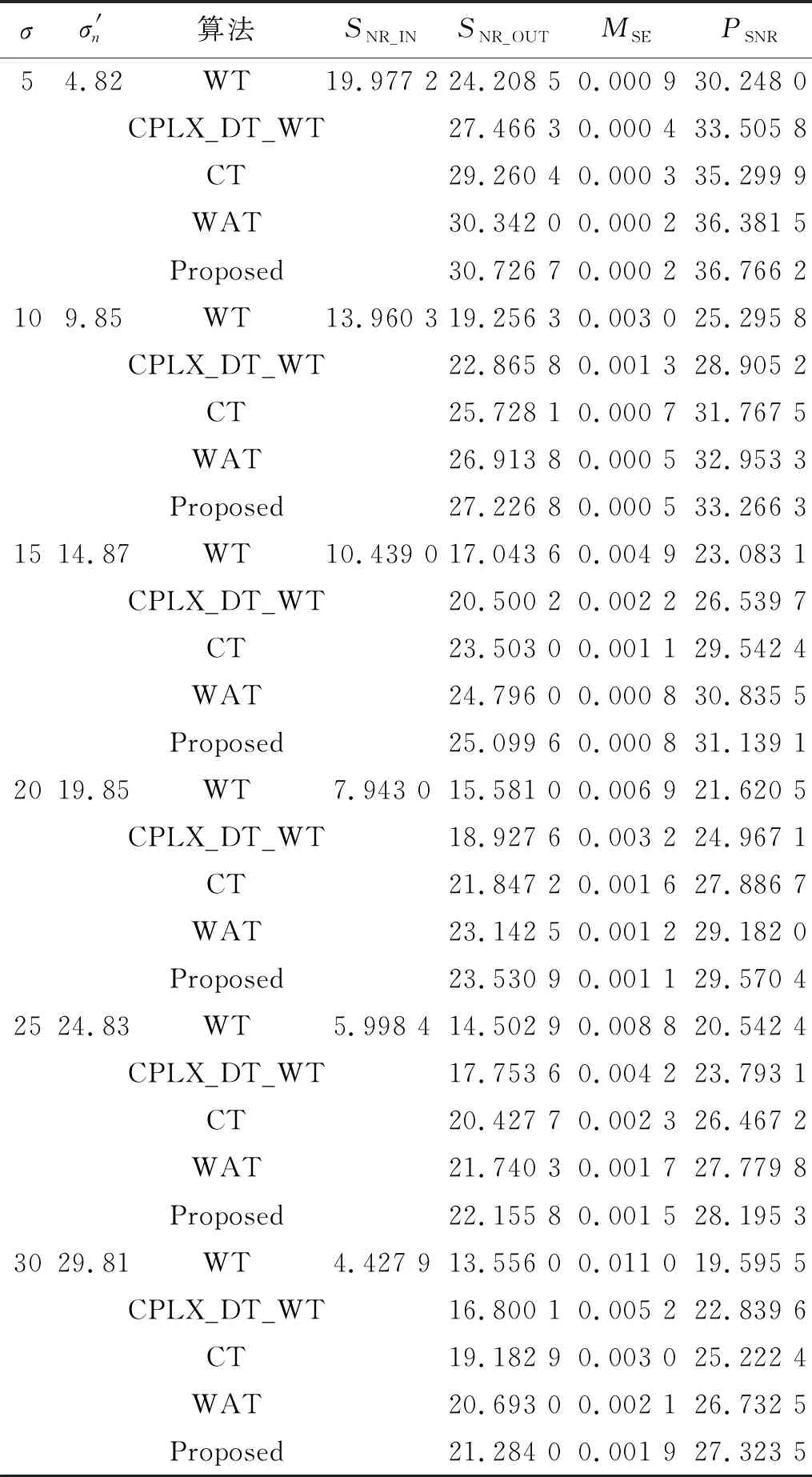
表3 实际地震信号去噪评价指标Tab.3 Denoising evaluation index of real seismic signal

首先从图6(a)和图6(b)可知，WT与CPLX_DT_WT去噪算法的去噪效果较差，仍可在表面观察到噪点的存在，未完全去除噪声，这是由于WT算法运算简单，算法复杂度较低，对复杂的地震信号处理存在一定劣势，但运算速度较快。从图6(c)、图6(d)、图6(e)可知，其余三种去噪算法较好地完成了去噪，表面几乎观察不到噪声的存在。三维图的表面以及去噪结果切片图中都不再含有噪点，可观察到地震信号清晰的纹理与结构。其次从表5中也可以定理分析出，除本文算法之外的其它几种对比算法，去噪效果最好的是WAT算法，其次是曲波算法、双树复小波算法以及小波算法，证明了波原子相对曲波、双树复小波以及小波对地震信号的处理优势。去噪效果最佳的是本文算法，证明了本文算法中用到的分层阈值选取及阈值修正、改进阈值函数以及循环平移等处理手段的有效性，表明本文算法的准确性。

5 结 论

(1)波原子作为一种新型多尺度几何分析工具，能够比小波、曲波、Gabor原子等工具更稀疏的表示纹理丰富的地震信号，本文提出的基于波原子变换的三维地震信号盲去噪算法，直接将含噪三维地震信号进行去噪，且无需给出噪声的标准差，提高了去噪效率。该算法的创新点主要为：①结合基于块的噪声估计算法对含噪地震信号进行噪声估计，用于盲去噪；②采用分层多尺度阈值，并进行阈值修正；③对阈值函数进行改进，改善硬阈值、软阈值的缺陷；④利用循环平移解决伪吉布斯现象，并提升地震信号的去噪效果。

(2)本文提出的阈值修正与改进阈值处理函数，结合噪声估计与循环平移算法，较好地完成了合成三维地震信号与实际三维地震信号的去噪，在SNR_OUT，MSE，MAE及PSNR等效果指标上要优于小波变换、双树复小波变换、曲波变换以及传统波原子变换去噪算法，表明了本文算法的有效性与准确性，为地震信号的变换域去噪提供了一种新思路。下一步工作将继续研究阈值选取与修正、改进阈值函数等，使其更加具有自适应性。