基于小波形函数的动态荷载识别方法

贺文宇，汪 洋，任伟新

(合肥工业大学 土木与水利工程学院，合肥 230009)

结构动态荷载识别是结构健康监测领域的热点问题[1-4]。其识别方法一般可归为两类：频域法和时域法。频域法和时域法分别基于频率响应函数和脉冲响应函数建立动态荷载与结构响应之间的关系，来估计动态荷载。与频域法相比，时域法结果通常具有更明确的物理意义和相对较高的精度,因此近年来得到了越来越多的关注。

时域动态荷载识别法大多数都是在时域内假定动态荷载在每一离散的采样时间间隔内为常数，将动态荷载表示为单位矩形脉冲信号之和，对应的动力响应表示为单位矩形脉冲响应之和的形式。简化荷载与实际荷载的误差，取决于矩形脉冲的脉宽即采样的时间间隔，间隔愈小，误差越小。为准确描述动态荷载，需要采用较高的采样频率，但这将导致所形成的脉冲函数响应矩阵及对应的荷载-响应方程组维数过大和待求系数过多，增加系数矩阵的病态性，从而使数值求解困难和效率低下[5-6]。为平衡识别精度和效率，众多学者采用一组基函数来拟合动态荷载，把直接求解动态荷载转化为求解荷载基函数系数，缩减荷载-响应方程组维数，减少待求系数个数[6-7]。

基函数方法是全域函数，与结构分析中的Rize方法类似，难以适应复杂的动态荷载和响应，而且形成的荷载-响应方程组的系数矩阵为非稀疏矩阵，给后续计算带来很大的挑战。鉴于此，众多学者引入荷载形函数的概念，利用常规结构有限元分析理论中的位移形函数拟合动态荷载[8]。基于形函数方法的识别精度主要取决于离散时间单元的长度，然而离散时间单元的长度难以事先确定。本文提出了一种基于多尺度小波形函数和时域反卷积的动态荷载识别方法，有效避免预先确定离散时间单元长度的难题。通过不同结构的数值算例验证了方法的可行性。

1 多尺度小波形函数

1.1 多分辨率小波分析

多分辨率分析是小波的最重要的特征之一[9-10]，它使小波能够以动态多尺度方式来逼近函数。利用小波逼近函数，可在不同尺度空间中得到不同的逼近精度。例如函数可在低尺度空间近似为

(1)

(2)

在小波空间V0中加入0尺度小波函数ψ0，l，形成V1空间，可提高逼近精度。

(3)

式中：C0，l为Ψ0，l对应的小波系数。

c0,l=〈f(x),ψ0,l(x)〉

(4)

当j→∞时，将逼近精确的函数。

(5)

1.2 拉格朗日小波形函数

常用的小波函数主要有样条小波、Daubechies小波、Hermite小波、Lagrange小波和三角小波等。本文采用计算方便的第二代拉格朗日小波，来实现动态荷载识别。当定义在区间[0,1]内,0尺度下的第二代拉格朗日小波为

(6a)

(6b)

j尺度下对应的小波函数ψj,l(x)为

(7)

第二代拉格朗日小波尺度函数(V0)、小波函数(W0,W1以及W2)如图1所示。

2 动态荷载识别

基于小波函数优越的多分辨率特性，对结构进行分析时，可在低尺度空间获得初始解，然后通过逐渐添加将小波函数，提升空间尺度，进而得到更精确的结果。本节将拓展小波多分辨率特性到基于时域反卷积法的动态荷载识别领域。

图1 拉格朗日小波形函数Fig.1 Lagrange wavelet shape functions

假设结构初始条件为零，结构动力响应y(t)可表示为外部动态荷载的卷积积分f(t)以及相应的脉冲响应函数h(t-τ)[11]。

(8)

式(8)可以转换为离散形式

(9)

式中：Δt为离散时间间隔，利用该方程可通过结构响应y(t)和脉冲响应函数h(t-τ)识别动态荷载时程f(t)。为获得较高的识别精度，通常需要采用小的离散时间间隔Δt，但过小的时间间隔会导致过多的待定系数，不仅增加计算成本，而且加重问题的病态性。

本节采用与结构有限元法类似的思路，将动态荷载在时间域离散化为局部时间单位，并通过二代拉格朗日小波形函数逼近荷载，进一步组集所有时域单元的小波形函数的动力响应，建立基于小波形函数的荷载-响应矩阵，识别结构动态荷载。

假定在整个时域内动态荷载被离散化为p个时间单元，每一个单元包含q个数据点，总数据样点为r=p(q-1)+1，因此式(9)可改写为

Y=KD

(10)

(11)

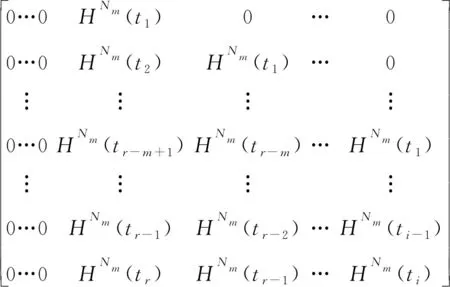
(12)

式中：HNm为由mth形函数Nm表示的荷载引起的动态响应。

式(10)中的系数矩阵K通常病态的，由系数矩阵K和响应列阵Y难以直接获得形函数系数D的稳定解。为此，通常将其转化为如下Tikhonov正则化问题

(13)

式中:λ为正则化因子，可由L曲线法来确定的。

通过式(13)求得小波形函数系数后，动态荷载可通过式(14)获得

F=DN

(14)

式中：F和N=[N1,N2,…，Nr]T分别为识别的动态荷载和小波形函数。

(15)

将式(15)代入式(10)和式(13)，求得待定小波系数，并通过式(14)，即可识别动态荷载，将对应的结果称为j尺度解。显然，高尺度解的精度高于低尺度解。

加快河湖长制立法步伐，完善河湖治理管护法规制度体系，为维护河湖健康、实现河湖功能永续利用提供法制保障。

基于二代拉格朗日形函数的多分辨率特性和时域反卷积法，可对动态荷载进行识别，其具体步骤如下：

步骤1将动态响应在时间域离散化为局部时间单元；

步骤2采用有限元法计算小波形函数荷载对应的动力响应；

步骤3组集所有时间单元的小波形状函数响应，形成0尺度系统荷载-响应矩阵，得到0尺度解；

步骤4提升小波尺度和增加测点响应信息，得到1尺度荷载-响应方程，并获得相应的1尺度解，提高识别精度；

步骤5检查收敛性，主要比较相邻尺度解之间的差值，决定是否继续提升求解尺度。

3 数值算例

通过悬臂梁和单层刚架算例验证了本文提出的自适应动态荷载识别方法的可行性和有效性。数值算例采用有限元方法计算动态响应，时间步长为0.001 s。为了模拟真实的测试环境，在精确的位移响应中引入5%随机高斯噪声[12-13]。

图2所示的悬臂梁长度L=16 m，弹性模量3.3×1011N/m2，密度2.5×103kg/m3，横截面面积A=1×4 m2。表1列出了两种工况、荷载时程、加载位置和测试位置。将整片梁等分成16个梁单元，建立有限元模型，计算动力响应。

图2 数值悬臂梁Fig.2 The simulated cantilever beam

表1 数值算例模拟工况Tab.1 Scenarios considered in the numerical simulations

工况B1中，识别过程分为0，1，2，3四个尺度。将整个动力响应时间程等分为50个时间单元。首先采用0尺度二代拉格朗日尺度函数和时间点为t=0.2Vs(V=0,1,…，50)的动力响应构成如式(14)的0尺度荷载-响应方程(阶数为51×51),进而将荷载-响应方程转化为如式(14)的Tikhonov正则化问题，获得0尺度解。图3和图4分别给出工况B1中动态荷载的识别结果和误差。进一步将0尺度的小波函数和时间点为t=0.1+0.2Vs(V=0,1,…,49)的动力响应加入0尺度荷载-响应方程，将其提升为1尺度方程(阶数为101×101)并求解，识别结果和误差如图3和图4所示，识别精度得到了有效提高。与此类似，可得到2尺度荷载-响应方程(阶数为201×201)和3尺度荷载-响应方程(阶数为401×401)，2尺度和3尺度解，如图3和图4所示。随着荷载-响应方程尺度的提升，阶数和计算量逐步增大，荷载识别的精度逐步提高，0～3尺度解的最大误差分别为0.8 N,0.2 N,0.05 N,0.01 N，相对误差约为40%,10%,2.5% 和0.5%。

(a)0尺度和1尺度

(b)2尺度和3尺度图3 工况B1动态荷载识别结果Fig.3 The identified dynamic force in case B1

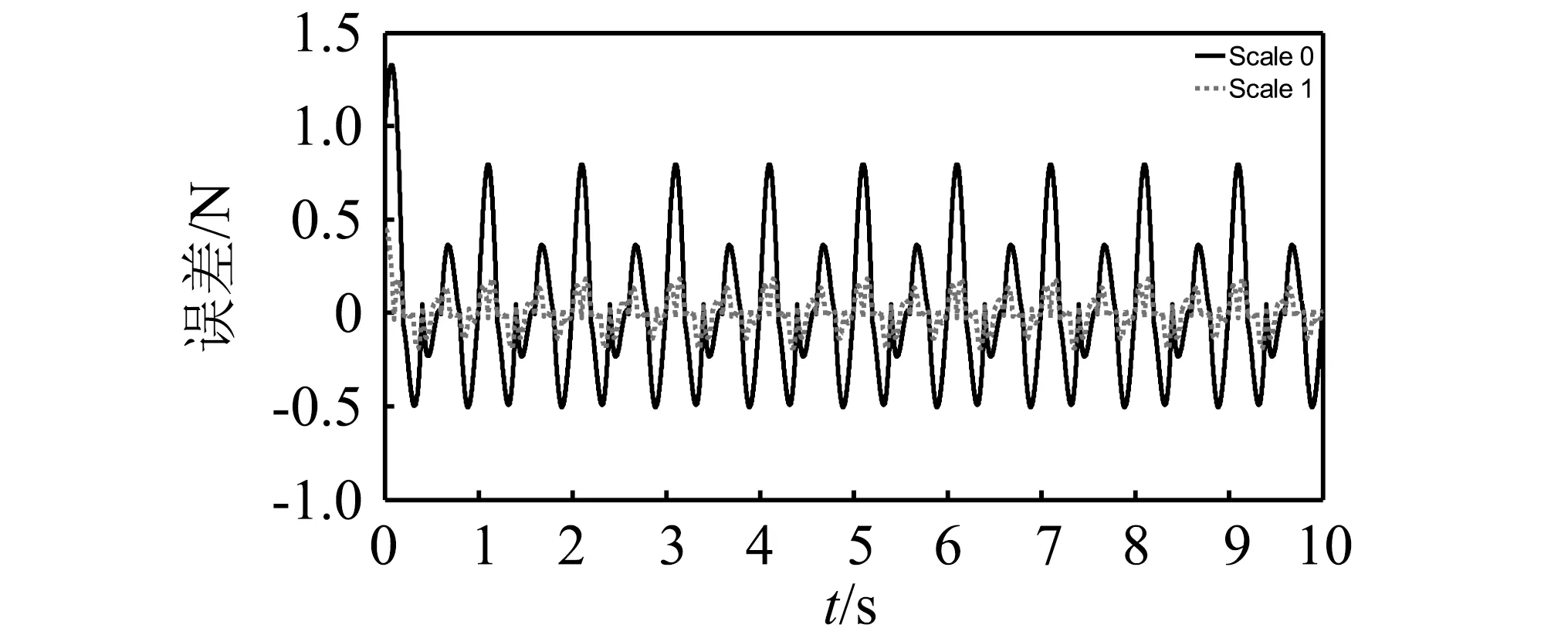
(a)0尺度和1尺度

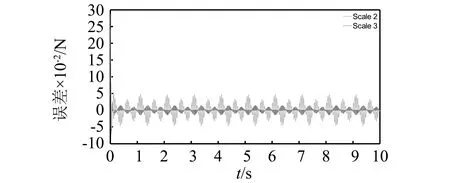
(b)2尺度和3尺度图4 工况B1的识别误差Fig.4 The identification error in case B1

鉴于4尺度解与3尺度解相比，识别精度提升有限，说明三尺度解的精度已经接近真实解，尺度不再提升，此外后续算例只采用0，1，2三个尺度解。值得注意的是，荷载-响应方程的升阶过程中，只有部分行和列需要增加，这可以有效减小计算量，提高识别效率。采用同样的过程，对工况B2进行分析，其识别结果和误差，如图5和图6所示。

图7所示的单层刚架，梁和柱的长度均为4 m，弹性模量3.3×1011N/m2，密度2.5×103kg/m3，梁和柱的截面积均为A=1×1 m2。每根梁和柱均被分为四个梁单元，建立有限元模型。表1列出了本算例中考虑的两种工况、荷载时程、加载位置和测量位置。

图5 工况B2动态荷载识别结果Fig.5 The identified dynamic force in case B2

图6 工况B2的识别误差Fig.6 The identification error in case B1

图7 数值单层框架Fig.7 The simulated single-story frame

采用与工况B1同样的过程，对工况F1和F2进行分析，图8和图9分别给出工况F1中荷载识别结果和误差；图10和图11分别给出工况F2中荷载识别结果和误差。

图8 工况F1动态荷载识别结果Fig.8 The identified dynamic force in case F1

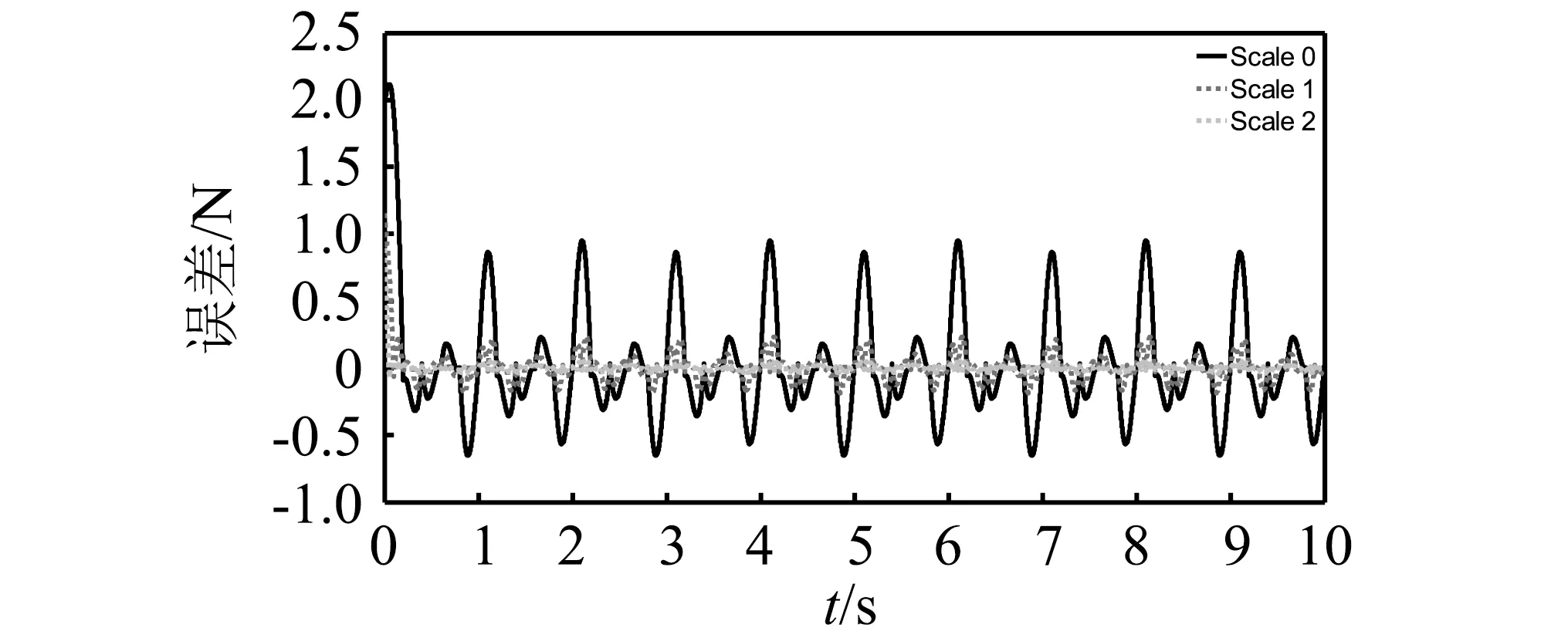
图9 工况F1的识别误差Fig.9 The identification error in case F1

图10 工况F2动态荷载识别结果Fig.10 The identified dynamic force in case F2

图11 工况F2识别误差Fig.11 The identification error in case F2

数值算例结果表明，随着荷载-响应方程尺度的提升，荷载识别的精度逐步提高，而且实施过程中，尺度可根据实际需要决定，而无需事前决定。如工况B1采用四个尺度，其它工况采用三个尺度。悬臂梁和单层框架的不同工况数值算例验证了本文提出的基于多尺度小波形函数和时域反卷积的动态荷载识别方法的可行性。

4 结 论

基于形函数的方法具有减少未知量数量和提高识别效率的优势，近年来在动态荷载识别领域的吸引了众多学者的兴趣。本文提出了一种基于多尺度小波形函数和时域反卷积的动态荷载识别方法，有效避免了预先确定离散时间单元的长度的难题。

基于小波形函数的动态荷载识别方法在时域内动态荷载进行离散化处理，并以小波尺度函数在时域单元内近似地逼近动态荷载，进一步组集所有时域单元的小波形函数的动力响应，建立基于小波形函数的荷载-响应矩阵，识别结构动态荷载。通过提升小波尺度来提升荷载-响应矩阵尺度，提高动态荷载识别精度。悬臂梁和单层框架数值算例验证了该方法的可行性。后续将进一步通过实验室试验验证该方法的有效性。