基于MSST的旋转机械故障诊断研究

2019-06-13黄传金雷文平李凌均孟雅俊

振动与冲击 2019年8期

黄传金，陈宏，雷文平，李凌均，孟雅俊,赵静

(1.郑州工程技术学院机电与车辆工程学院，郑州 450044；2.浙江大学机械工程学院，杭州 310007；3.郑州大学机械工程学院，郑州 450052)

单变量信号的调幅-调频模型含有振动信号的频率、幅值等信息，是分析振动信号的强有力的工具[1]。因旋转机械故障的位置不同、刚度和阻尼变化等原因，故障时的振动信号往往表现出非平稳性，而且不同方向的振动信号强度和频谱结构可能存在差异[2]。根据旋转机械回转特性可知，稳态时转子同一截面互相垂直方向上各谐波的运动轨迹为椭圆[3]。据此原理，基于同源信息融合技术的全息谱和全矢谱分别被提出，其中，全息谱以图的形式将各谐波的椭圆轨迹展现出来；全矢谱以傅里叶谱的形式将椭圆长轴、短轴表现出来。

考虑基于傅里叶变换的全息谱和全矢谱难以融合两个非线性的信号，与经验模态分解(Empirical Mode Decomposition，EMD)[4]和局部均值分解(Local Mean Decomposition，LMD)[5]联合的同源信息融合技术被提出，即分别先对两个信号进行自适应分解，然后按一一对应原则用全矢谱对分解结果进行融合。但用EMD和LMD分解不同通道信号时，分解结果可能不统一，给后续的信息融合造成困难[6]。

文献[7]和文献[8]分别将EMD和LMD扩展到二元领域，提出了二元经验模态分解(Bivariate Empirical Mode Decomposition，BEMD)和复局部均值分解(Complex Local Mean Decomposition，CLMD)以处理二元信号。BEMD和CLMD均将两个通道的信号作为一个整体来分解，可保证有统一的分解尺度，易于信息融合。因此有学者提出了联合BEMD和全矢谱[9]以及CLMD和全矢谱[10]的旋转机械故障方法。但基于傅里叶变换的全矢谱技术难以处理时变的信号，而且BEMD和CLMD分别是在EMD和LMD基础上发展而来，在分解频率相近的信号时存在模态混叠问题。

时频分析是一种强有力的非线性信号分析工具，Daubechies 等[11]提出同步压缩小波变换(Synchrosqueezing Transform，SST)。SST能有效地将小波变换后的时频图进行重组，获得较高频率精度的时频曲线，可将任意信号分解为若干个近似谐波的线性叠加，可对压缩后的信号重组，是一种类似于EMD的算法，具有EMD的自适应性；对小波母函数不敏感，克服了小波变换对小波基选取的困难。文献[12]将SST应用于识别时变结构频率；文献将[13-17]运用SST进行故障诊断。然而，这种方法大多依赖于单成分的前提。对于复杂的多分量非平稳信号，信号成分分量不仅可以随时随地变化，而且它们的瞬时频率曲线也可能彼此非常接近，甚至在频域中重叠，从而不能被小波变换分离，甚至导致模糊。

为分析多通道信号，Ahrabian等[18]将SST扩展应用到多元领域，并使用联合瞬时频率概念以便识别多个数据通道的振荡特征，海洋浮漂漂移数据和双变量多普勒雷达数据说明该方法的可行性和有效性。

在旋转机械故障诊断领域，随传感器技术的发展，同时获取多通道的振动信号已非常普遍。如大型转子的现场检测，一般采用非接触式电涡流传感器正交安装在某一支撑截面，然后采集正交方向的振动信号，即使是某个传感器出现故障，也能进行现场监测。但与之匹配的多通道振信号的时频分析技术还比较缺乏，故提出基于双变量同步压缩(Multivariable Synchrosqueezing，MSST)的旋转机械故障时频分析新方法，以综合双通道信号的时频信息，并能兼容分析单通道的信号。试验结果表明所提方法可以分析频率相近的信号，获取的时频曲线有较高的聚集性，噪声也被较好地抑制，还可兼容分析单通道振动信号。

1 正交双变量信号联合瞬时频率

1.1多变量调制振荡模型

单变量信号可通过调幅模型表示

x(t)=a(t)cosφ(t)

(1)

式中：a(t)和φ(t)分别为信号x(t)的瞬时幅值和频率，称为一个规范对。对x(t)进行Hilbert变换，可得相应的解析信号x+(t)

x+(t)=a(t)eiφ(t)=x(t)+iH{x(t)}

(2)

近年，基于单变量调幅-调频模型概念扩展到多变量领域，以便使用众所周知的联合瞬时频率和带宽的概念对多通道信号的联合振荡结构进行建模。对多变量信号x(t)，熊伟等在每个时刻t构造一个向量，给出相应多元解析信号模型x+(t)。

(3)

式中：an(t)和φn(t)为第n个通道信号的瞬时幅值和频率，n=1，2，…，N，N为总的通道数。Feng等提出了多变量数据的联合瞬时频率ωx(t)和联合瞬时带宽υx(t)的概念以便对多变量的信号进行建模。

ωx(t)捕捉多变量信号的组合振荡动态特性，而υx(t)捕获每个通道中的多变量振荡相对于联合瞬时频率的偏差。ωx(t)和υx(t)形式为

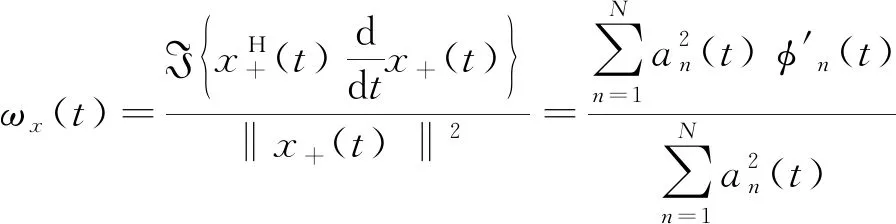
(4)

(5)

1.2 正交双变量振动信号调制振荡模型

正交双变量振动信号是指运用传感器采集的旋转机械某一支撑截面上互相垂直方向的振动信号。根据多元信号解析模型公式，令N=2，可得到正交双变量信号的解析模型为

(6)

对应的联合瞬时频率ωx(t)和联合瞬时带宽υx(t)形式为

(7)

(8)

1.3 各向同性时正交双通道信号联合瞬时频率

(9)

旋转机械各向同性时，联合瞬时频率即为单个通道振动信号的瞬时频率。因为实际测量的信号往往含有噪声，即使对单分量的信号，直接运用式(9)，通过差分的方法获得瞬时频率通常超出了信号频率范围，而通过式(4)求取的瞬时频率可解决这一问题。

1.4 各向异性时正交双通道信号联合瞬时频率

(10)

此时，联合瞬时频率表示为所有通道瞬时频率的功率加权平均。较之单通道信号频率，联合瞬时频率包含了所有通道信号的瞬时频率，频率特征更为丰富，反映了两个通道频率的变化情况。

通过式(9)和式(10)可知，正交采样时，即使缺少了某个方向传感器的数据，也能求出联合瞬时频率。只是此时联合瞬时频率不能捕捉两个通道信号的组合振荡动态特性，而变为单个方向振动信号的瞬时频率，说明了所提方法具有兼容分析单通道信号的能力。

需要指出的是，由于本文试验所用的双变量信号是通过正交采样技术获取的，所以本文强调了正交性。其实，由于没用到两个方向振动信号的相位信息，对于一般的双变量信号，本文所提方法同样适用，“4.1节”中的仿真信号分析结果证明了这一点。

2 同步压缩小波变换

同步压缩小波变换是应用于连续小波变换的后处理技术，以便表征非平稳信号的局部时频信息。对于给定的小波母函数ψ(t)，时变信号x(t)的小波变换为

(11)

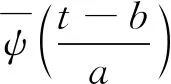
(12)

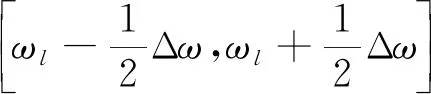
(13)

较之其它的时频重组算法，如短时傅里叶变换、小波变换等，SST可清楚描述、提取时变谱中的各分量；而且SST是可逆的，可重构单变量的调制振荡信号，如式(14)所示

(14)

由于SST可将小波变换后的时频图进行压缩重组，所遇获取的时频曲线更细、更清晰；而且在同步压缩过程中，丢掉了幅值很小的小波系数，噪声对分析结果影响较轻。

3 基于MSST的时频分析方法

3.1 时频域划分

如果调制振荡分量对于每个信道是已知的，可以通过式(7)求取联合瞬时频率。为此，首先将时频域划分为K个频段{ωk}k=1,2,…,K。这使得有可能从给定的多变量信号中识别一组匹配的单组分信号。

通过自适应频率拼接技术的多变量扩展来划分时频域，核心思想是根据多变量带宽确定多变量单组分信号。将时频域的频率划分为2l个相等宽度的频带，每一个带宽ωl,m为

(15)

式中：l=0,1,…,Ls为频带的层数，通常Ls=5；m=0,1,…,2l-1是频带索引。然后计算给定频带ωl,m的多变量带宽Bl,m，其中ωl,m被分成两个频率子带ωl+1,2m和ωl+1,2m+1，如下所示：

(1)如果频带ωl,m包含多变量单组分信号，那么Bl,m≤Bl+1,2m+Bl+1,2m+1。

(2)如果每个频率子带包含单独的多元单组分信号，那么Bl,m>Bl+1,2m+Bl+1,2m+1。

给定具有两个信道的双变量信号x(t)，对于给定频带ωl,m，每个信道的SST系数可由T(ωl,b)得到，即通过计算SST系数倒数的傅里叶变换来获得

(16)

式中:F{·}为傅里叶变换算子；Rψ为标准化常数；Φl,m(ω)∈RN，是一个列向量。

自适应频率标度基本原理如下：如果初始多变量带宽是针对整个信号在l=0处计算的，则基于以下条件来分割带宽

(17)

其中，

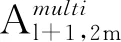
式(14)的右侧影响频率子带的总能量，因此，不考虑具有可忽略信号内容的子带。最终的系列自适应频带由{ωk}k=1,2,…,K给出，K是振荡尺度的数量，并且ω1>ω2>…>ωK。

3.2 双变量时频表征

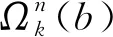
(18)

(19)

(20)

(21)

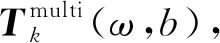
(22)

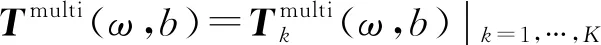
3.3 基于MSST的旋转机械故障诊断时频分析方法

建议的基于MSST的旋转机械故障诊断时频分析方法如下：

步骤1 通过正交采样技术采集两个通道的振动信号，组成一个双变量信号x(t)；

步骤2运用SST获取同步压缩值Tn(ω,b)；

步骤4根据式(20)和式(21)计算双变量信号的瞬时频率和振幅；

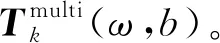
运用双变量同步压缩小波变换可获取两个通道内的频率变化情况，提供的时频信息较为全面、准确，而且也可兼容分析单通道的振动信号。

4 案例分析

4.1 仿真信号分析

旋转机械各相同性时，每个方向振动信号的频率相同，故构造一组频率成分相同而幅值不同的信号，由谐波信号、调幅信号和调频信号组成，如式(23)和式(24)所示

x(t)=sin 2πf1t+0.8cos 2πf2t+(1+0.6cos 18πt)×
sin 2πf3t+0.7sin(2πf4t+1.5cos(10πt))+
0.1rand(1,n)

(23)

y(t)=0.7sin 2πf1t+0.5cos 2πf2t+
(1+0.8cos 18πt)×sin 2πf3t+

0.8sin(2πf4t+1.2cos(10πt))+0.1rand(1,n)

(24)

式中：f1=32 Hz；f2=38 Hz；f3=128 Hz；f4=196 Hz。

信号x(t)的傅里叶谱，x(t)，y(t)基于双变量信号的同步压缩变换时频分析结果以及各自信号的SST结果，如图1所示。

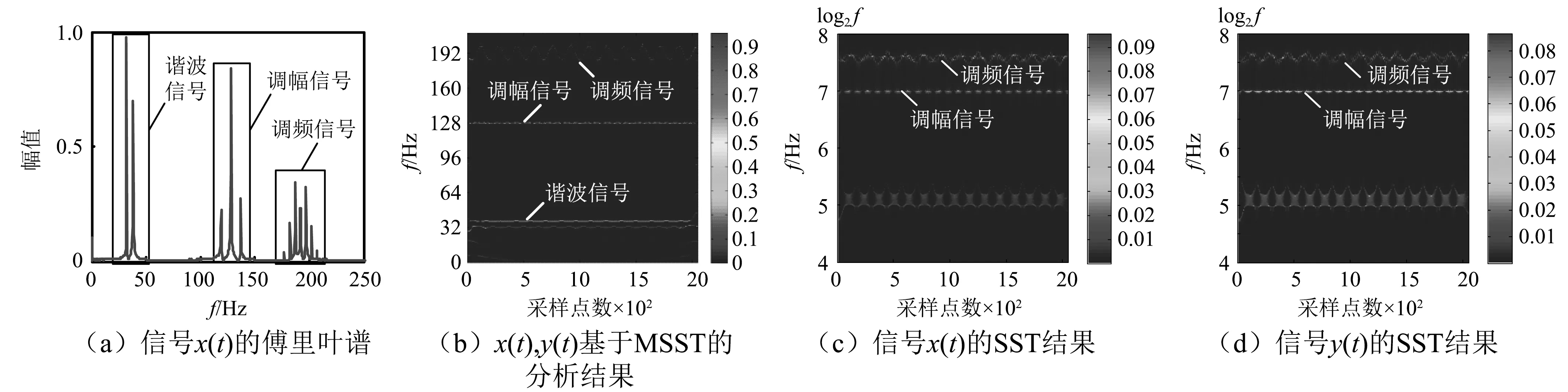
图1 信号x(t)的傅里叶谱、本文所提方法的分析结果以及各自信号的SST结果Fig.1 FFT spectrum of signal x(t),analysis results of the method proposed in this paper and SST result of each signal

从图1(b)可知，本文所提方法较好的提取了谐波信号、调幅信号和调频信号频率；从图1(c)，图(d)中x(t)和y(t)的SST结果可知，SST可提取调频信号和调幅信号特征频率；当SST分析瞬时频率比较接近的低频分量时，不能很好的提取两个低频分量的频率，并且在频域中重叠，导致模糊，与Feng等研究中的分析结果一致；本文所提方法不存在这一现象。

为体现本文所提方法可融合不同成分信号的频率频率信息，在式(24)基础上，为y(t)增加了0.5cos 2π50t的谐波成分，其余的不变；本文所提方法分析结果以及y(t)的SST分析结果，如图2所示。

(a)本文所提方法分析结果

(b)信号y(t)基于SST的分析结果图2 本文所提方法分析结果以及y(t)的SST分析结果Fig.2 The results of the proposed method and the analysis results of y(t)based on SST

从图2(a)可知，本文所提方法不仅有效提取了调频信号、调幅信号的频率特征以及频率相近的谐波信号特征频率，还融合了信号x和y的频率信息，包含了频率相近的三个谐波成分32 Hz，38 Hz和50 Hz。

4.2 转子各向同性时的双稳态信号分析

数据来自屈梁生院士所著《机械故障的全息诊断原理》一书中的双稳态行为案例。分别将风机前端支撑处水平和垂直方向的信号x,y(采样频率fs=2 000 Hz，采样点数为1 024，转速为5 625 r/min)组成二元信号x(t)。左、右两端支撑处水平、垂直方向的信号及其相应的傅里叶谱，如图3所示。

图3 x，y的平面图、三维图及其傅里叶谱Fig.3 2D,3D and Fourier spectra of x,y

从图3(a)和图3(b)可知，转子从一个稳态跳跃到另外一个稳态，发生了双稳态行为。从图3(c)和图3(d)所示的傅里叶谱可知水平和垂直方向的振动信号的频率相同，均为93.75 Hz，故可认为转子各向同性；另外，垂直方向的振动信号幅值大于水平方向的。但傅里叶谱不能表述图3(b)所示的幅值变化情况。

运用本文建议的基于MSST的时频分析方法处理二元信号x(t)以及用HHT分析信号x，得到时频分析结果如图4所示。

将图4(b)和图1(c)、图1(d)对比可知，图4中的瞬时频率仅有一个分量，且和各个通道信号的频率成分一致，验证了式(9)指出的：旋转机械各向同性时，双通道振动信号的联合瞬时频率等于各个通道信号的频率。另外从图4(b)可知，转子在0.25 s时幅值发生了跳变，但频率没有变化。对比图4(a)和图2(b)可知，通过MSST获取的时频曲线比较清晰，噪声也得到很好抑制，而且也不存在虚假低频分量。

(a)信号x的Hilbert-Huang谱

(b)转子双稳态信号的MSST时频分析结果图4 转子双稳态信号的时频分析结果Fig.4 The Hilbert-Huang spectrum of the signal x

4.3 转子不对中松动碰摩复合故障信号分析

在柔性转子试验台设置不对中松动碰摩复合故障信号(转速为28 r/s)；采用正交采样技术获取的水平方向和垂直方向的振动信号分别为x和y(采样频率为2 048 Hz，采样时长0.5 s)。x,y组成的平面图、三维时域图及其傅里叶谱，如图5所示。将信号x,y组成二元信号x(t)，运用本文建议的基于MSST的时频分析方法处理二元信号x(t)以及用HHT分析信号x和各自信号SST的时频分析结果，如图6所示。

图5 转子不对中松动碰摩复合故障信号及其傅里叶谱Fig.5 Composite fault signals and their spectrum

对比图5(c)和图5(d)可知，信号x比y多了3X成分(X=28，代表基频)，其余二者均含有X，2X，4.5X和5.5X，但y中的2X成分较大，另外信号x和y在152 Hz存在两个对称的边频带，两个边频带均与152 Hz相距28 Hz。由图6(a)可知，基于MSST的时频分析结果含有信号两个通道的瞬时频率成分，而且在5.5X附近频率是瞬时变化的，这一点在图6(b)、图6(c)和图6(d)均得到印证。较之Hilbert-Huang谱，MSST的时频分析效果不存在频率混叠现象，而且不也存在虚假的低频成分，频率分辨率较高；较之SST，本文所提方法不仅有效融合了信号x,y的频率信息，还提取了幅值较弱的3X特征频率，而基于SST的分析结果没有体现出3X特征频率。

图6 转子不对中松动碰摩复合故障时频分析结果Fig.6 Rotor misalignment composite failure time-frequency analysis results

4.4 磨煤机故障信号

某立式煤磨机结构及测点布置(太阳轮、行星轮为浮动部件无法布置振动测点)，如图7所示。电机轴承为一端固定一端浮动的配置，电机与磨机减速机分别座在磨煤机基础上，基础下面通过液压减振器支撑。电动机的水平轴与伞齿轮轴的小齿轮轴端相连接，伞齿轮的垂直轴承通过联轴器驱动由行星齿轮的三行星啮合点确定中心的太阳轮。行星齿轮架用螺栓与磨机磨盘固定，并以磨盘速度旋转。电机转速为990 r/min，小伞齿轮数为12。

图7 煤磨机传动系统及测点布置结构图Fig.7 The coal mill drive system and measuring point layout

采样频率为1 280 Hz，采样点数为2 048，采集的测点1水平和轴向振动信号、测点2水平和竖直方向的振动信号及其相应的傅里叶谱，如图8所示。用本文建议的方法分别对测点1、测点2的信号进行MSST时频分析，分析结果如图9(a)、图9(b)所示。总体而言，测点2的振动强度远小于测点1的，主要是因减速器整机刚度大，同样的激振力引起的振幅较小。图9(a)中测点1存在1X，2X，3X等低频成分和12X的啮合频率，可能存在轴不对中现象；由于啮合频率的幅值远高于低倍频的，可判断电机自由端轴承受的力主要来自小伞齿轮的啮合力，啮合力引起轴承轴向窜动，容易造成轴承摩擦损坏。从图9(b)可知，小伞齿轮存在1X，2X，和3X等低倍频信号和高频的调幅-调频信号；其中，边带是不对称的，啮合频率12X的下边带成分较多，而且调幅-调频信号是非线性的，总体上频带的间隔为转频X。从图9(b)中下边带成分较多可判断齿轮存在偏心故障。

图8 测点1、测点2采集的振动信号及其傅里叶谱Fig.8 Vibration signals collected at measuring points 1 and 2 and their Fourier spectra

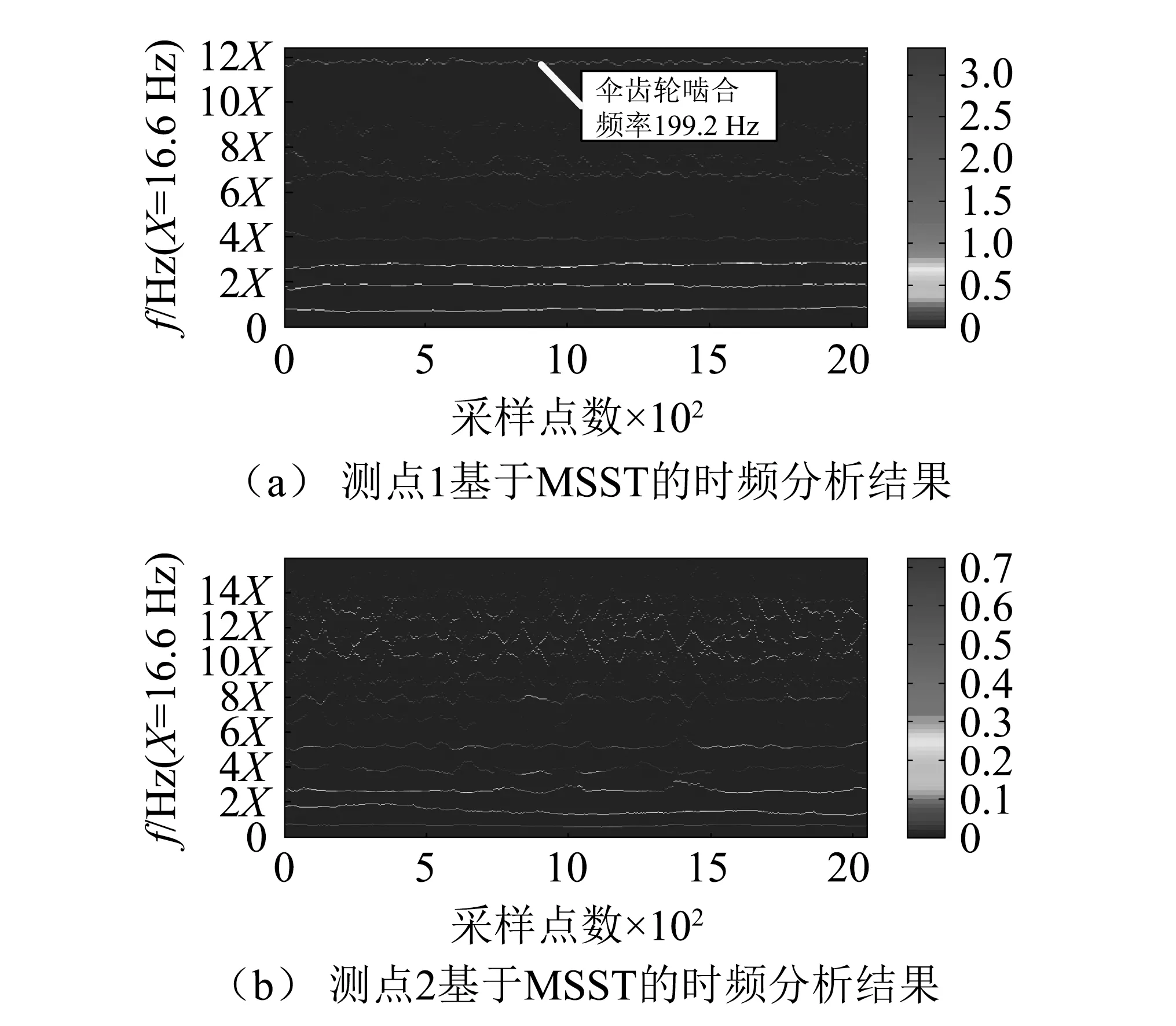
图9 测点1、测点2的双变量时频谱Fig.9 The bivariate time frequency spectrum of measuring point 1 and 2 signals

该磨煤机基础曾经两次打碎重做，电机自由端轴承也曾烧坏。综合图9(a)和图9(b)的分析结果和磨煤机工作特点可判断：磨煤机工作过程中的非平稳载荷导致调幅-调频信号是非线的；由于齿轮存在偏心故障使小伞齿轮进入和脱离啮合时的碰撞加剧，产生较大的冲击力，加上减速机本身传递的磨盘转矩、磨辊加载力及磨煤机振动产生的冲击力，导致该机基础、电机自由端轴承分别承受较强的竖直方向的冲击力和轴向力，进而引起了基础和轴承的损坏。

为验证所提方法可以兼容分析单通道的振动信号，假设因为传感器故障，测点1采集了水平方向的振动信号，其基于单通道的双变量分析结果，如图10所示。从图10可知，对于单通道的信号，所建议的方法也能很好地提取信号的时频特征，含有明显的1X，2X和3X，但啮合频率12X处的强度没有双通道信号的明显。