低雷诺数开缝圆柱绕流尾迹流场特性

邢鹏飞，孙志强

(中南大学 能源科学与工程学院，湖南 长沙，410083)

圆柱绕流是工程流体力学领域的热点研究课题[1-2]，其中所蕴含的流动分离、旋涡脱落和尾迹演化等流动现象长期以来是众多学者进行理论分析、数值模拟和科学实验的研究对象[3-4]，因此，对圆柱绕流尾迹流场特性的研究具有重要意义。此外，对圆柱进行合理设计和变形在设备减振[5]、流动减阻[6]、传热优化[7]和流量测量[8-9]方面具有重要应用价值。国内外学者运用实验测量和数值计算方法对开缝圆柱绕流进行了大量研究。在实验研究方面，IGARASHI[10-11]对 2个定相对缝宽圆柱在一定雷诺数范围内的流场特性进行了研究，对不同开缝角下的流动现象进行划分并对“自引入现象”和边界层的“吸吹作用”形成机理进行了探讨。OLSEN等[12]研究了不同类型的变形圆柱流场中旋涡脱落频率与雷诺数的关系及阻力系数的影响因素，并指出一定开缝角条件下的旋涡脱落频率比未开缝圆柱的高。ORDIA等[13]对圆管内平行开缝圆柱绕流进行了可视化实验，研究了旋涡生成机理。GAO等[14]对未开缝圆柱和平行开缝圆柱的尾涡模型进行了对比研究，发现未开缝圆柱尾涡脱落的反作用模式及其在开缝后的改变情况。PANKANIN[15]利用示踪技术研究开缝双圆柱发现，当开缝圆柱后侧形成的旋涡向下游运动时，其移动速度增大，而且流场中旋涡的间距也随着圆柱直径的增大呈现出线性增大的趋势。PENG等[16]在风洞和水洞中对不同相对缝宽的圆柱进行了测量，证明当相对缝宽在 0.10～0.15范围内时，旋涡脱落的稳定性最好，而且脱落频率与斯特劳哈尔数线性度最好，当相对缝宽为0.15时流场的二维性最好。谭广琨等[17]利用氢气泡显示技术研究了空心圆柱在相对缝宽和开缝角不同时的流动状况，发现较小的开缝角可以减小圆柱所受阻力，而且开缝角为 20°时效果最佳。同时，国内外学者利用各种流动模型对开缝绕流进行了大量数值模拟研究。杨锦文等[18]利用大涡模型对开缝圆柱近尾流场进行了模拟研究，结果表明缝隙内流体的往复振荡对圆柱绕流的周期性产生了显著影响，开缝圆柱的旋涡脱落频率和斯特劳哈尔数均比相同雷诺数下未开缝圆柱的高。刘志荣等[19]利用POD方法对开缝圆柱流场信息进行了重建，研究了开缝角对于旋涡脱落的敏感性。王慧等[20]对以开缝圆柱为旋涡发生体的流量计进行了仿真，证明开缝圆柱的旋涡信号强度和信噪比较高，尤其在相对缝宽为0.15时，旋涡信号质量最好。申春赘等[21]对圆内开缝圆不同开缝方向自然对流换热进行了研究，得到了不同开缝角的自然对流换热规律和特性。综上所述，不论是实验测量还是数值模拟，研究者大多是针对较大雷诺数进行的，而对于较低雷诺数的层流过程研究较少。为此，本文作者采用数值模拟的方法，应用商业软件Fluent对无限大流场内雷诺数为100的二维开缝圆柱绕流尾迹流场进行分析，探讨不同相对缝宽和开缝角时旋涡脱落和圆柱受力规律。

1 数值模型与计算方法

本研究对象为无限大流场中二维开缝圆柱绕流，其计算域如图1所示。开缝圆柱固定于流场中，计算域采用笛卡尔坐标进行描述，坐标原点位于圆柱中心，流体从左侧沿x方向流入，从右侧流出。圆柱直径d=20 mm，入口处及上下壁面到圆柱中心距离均为10d，圆柱中心到出口的距离为30d，流道宽度为20d。计算域范围为-10d≤x≤30d，-10d≤y≤10d。蒋赟等[22]发现，上述采用的计算域可以满足模拟无限大流场中圆柱绕流的要求。采用空气作为流动介质，密度ρ=1.225 kg·m-3，动力黏度μ=1.789×10-5N·s·m-2。入口为均匀来流，采用速度入口边界条件且速度U=0.073 m/s，出口采用压力出口边界条件，远场壁面为对称边界条件，圆柱壁面采用无滑移壁面。开缝圆柱结构示意图如图2所示。采用分割然后拉开的方式对圆柱进行开缝，开缝角α为开缝中心线与水平线之间的夹角，缝宽s为2个半圆柱之间的间距，圆周角φ为前驻点与圆周上任一点沿顺时针方向的夹角。

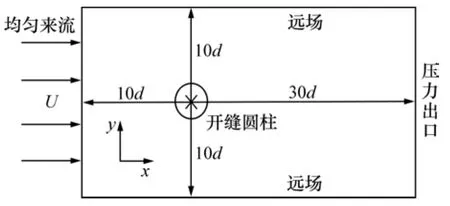
图1 计算域及基本设置Fig.1 Numerical calculation domain and basic settings

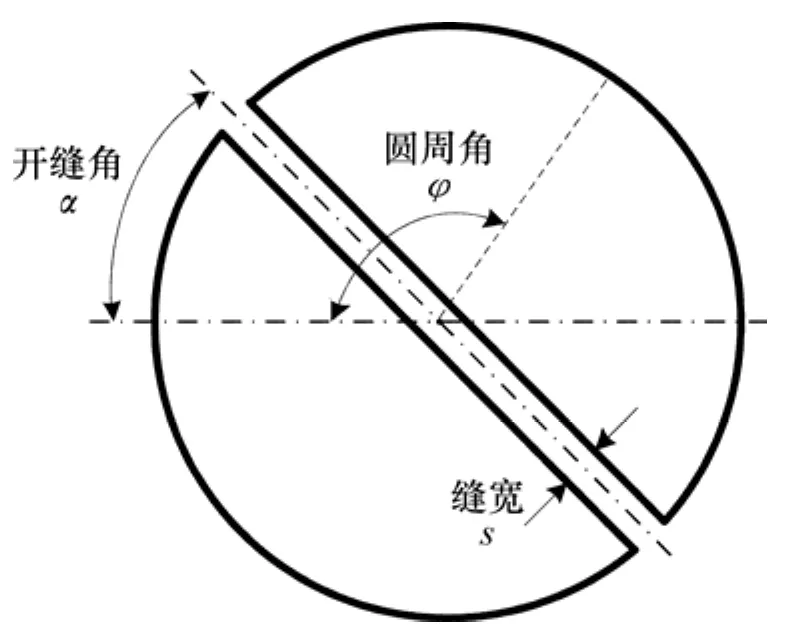
图2 开缝圆柱结构示意图Fig.2 Schematic diagram of circular cylinder with slit

本研究的雷诺数Re=ρUd/μ=100(其中，ρ，U和μ分别为流体的密度、来流速度和动力黏度；d为特征长度，本文取圆柱直径)，属于层流范围，因此，可忽略空气的压缩性和流场的三维性，采用二维模型进行计算。控制方程包括连续性方程和Navier-Stokes方程，即

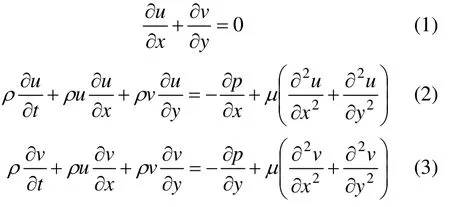
式中：u和v为速度分量；t为时间；p为压力。

根据桑文慧等[23]的研究，动量方程离散格式选择QUCIK格式，压力项离散格式选择Standard格式，非稳态项离散选择二阶隐式格式，压力速度算法选择SIMPLEC方法。考虑到圆柱绕流流场特性及计算精度和速度的影响，采用图3所示的结构化多块网格对流场进行划分。开缝圆柱前侧来流区、缝内和尾流区流体速度梯度大，流动现象复杂，因此，网格最致密；开缝上下端和尾流远场较稀疏，其他远离开缝圆柱区域速度变化小，流动现象简单，网格最疏松。

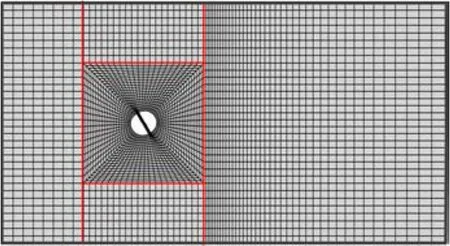
图3 网格划分图Fig.3 Schematic diagram of meshing

2 模拟结果验证

为了验证模型的准确性，利用上述模型对未开缝圆柱绕流流场进行计算，将提取得到的斯特劳哈尔数St、阻力系数Cd和升力系数Cl等流场特征参数与文献参考值进行对比。以上参数定义式分别如下：

式中：f为旋涡脱落频率；Fd和Fl分别为开缝圆柱所受阻力和升力。

在圆柱绕流过程中，Cd和Cl为时变量，因此，选择阻力系数的时均值Cd,avg和升力系数的均方根值Cl,rms作为流场特征参数。通过网格无关性验证发现，当网格数量达到95 430时，3个流场特征参数的计算值稳定，将其与文献值[24-26]比较，结果如表1所示。从表1可以看出：3个特征参数的模拟值与文献值之间的相对误差均在±3%以内，表明本模型和算法的精确度很高。

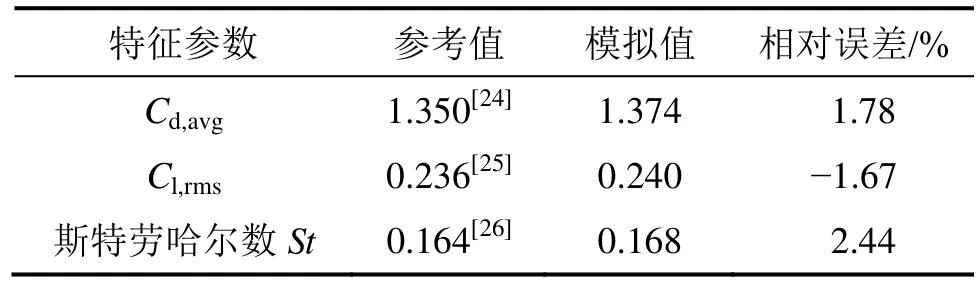
表1 流场特征参数验证Table 1 Verification of characteristic parameters of flow field

3 结果与讨论

以平行来流方向为基准，顺时针方向为正向，以相对缝宽(缝宽/圆柱直径即s/d为0.005，0.025，0.050，0.075 和 0.100)和开缝角(0°≤α≤90°，间隔为 10°)为自变量探讨开缝对圆柱尾迹的影响。

3.1 开缝圆柱尾迹演化过程

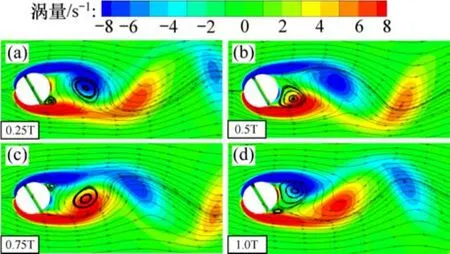
图4 开缝圆柱绕流尾迹演化过程Fig.4 Evolution processes of wake around circular cylinder with slit

当s/d=0.1，α=60°时，1个完整周期T内开缝圆柱绕流尾迹演化过程见图4。从图4可见：当t=0.25T时，开缝圆柱上侧旋涡开始脱落，下侧有逆时针旋涡生成，流体从左上侧缝隙入口流向右下侧出口，缝隙进口有顺时针旋涡生成；当t=0.5T时，上侧旋涡继续脱落，强度减弱，下侧旋涡在缝内流体冲击下不断变大；当t=0.75T时，下侧旋涡脱落，上侧有顺时针旋涡生成，缝内流体流向不变；当t=1.00T时，上侧旋涡不断变大并开始脱落，下侧有逆时针旋涡生成。相比未开缝圆柱旋涡脱落周期变化情况，开缝使得部分流体可以通过缝隙直接流向圆柱后侧，下侧旋涡生成频率有所增大。此外，缝隙对于圆柱上下侧流体的沟通作用使圆周压力分布情况出现变化，在一定程度上影响了开缝圆柱在流场中的受力情况。

3.2 压力分布与分离点

图5所示为s/d=0.1时开缝圆柱沿圆周方向的压力系数分布。从图5可见：前驻点(φ=0°)处压力系数最大，从前驻点至圆柱肩部最上侧流动区域减小导致流体速度不断增大、压力系数不断减小；从肩部上侧至后驻点(φ=180°)，边界层内的流体在黏性力作用下速度不断减小，因而，压力系数有所增大；当圆柱表面速度梯度减小至0时，开始发生边界层分离，旋涡开始形成；圆柱下侧压力系数分布与上侧对称，且不同相对缝宽时压力系数分布趋势相同，可见在本研究范围内相对缝宽对圆周压力分布影响较小；当雷诺数较高时，由于开缝圆柱后侧形成了强度更大的旋涡，在90°≤φ≤180°范围内随着开缝角度增加，圆周后侧压力系数波动不大，负压绝对值也更大[14]。图6所示为s/d=0.1时圆周压力系数最小值位置φ0分布。从图6可见：随着开缝角的增大，圆周上压力系数最小值有所减小，位置后移且移动幅度随相对缝宽的增大而增大，在s/d=0.1时，其值达到最大，Δφ0=6.11°。

图5 s/d=0.1时开缝圆柱沿圆周方向压力系数Cp*分布Fig.5 Distribution of pressure coefficient(Cp*)along circumference when s/d=0.1

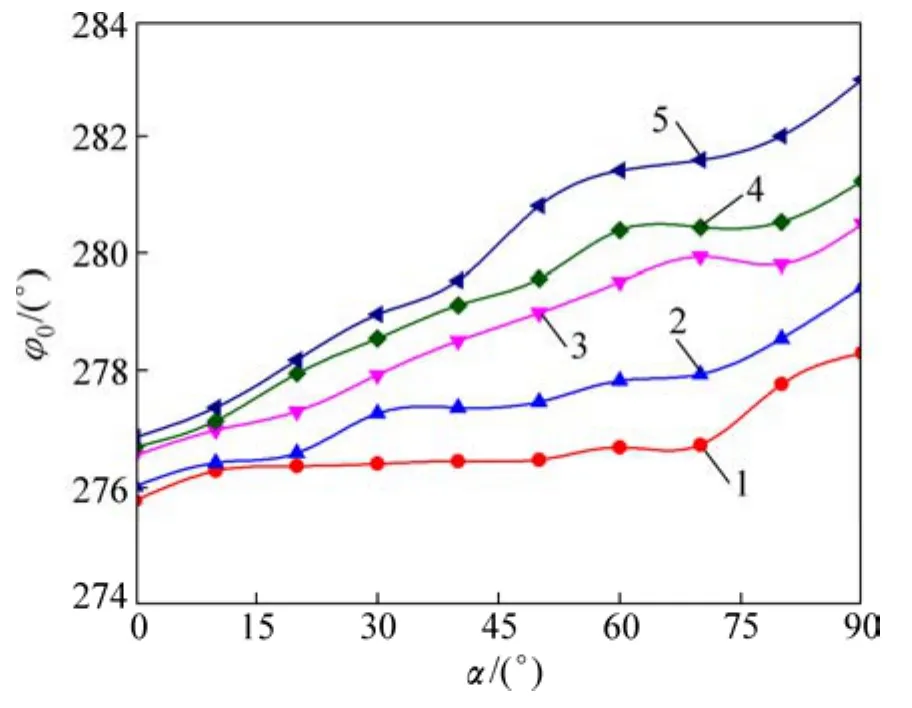
图6 不同开缝条件下圆周压力系数最小值所处位置φ0Fig.6 Distribution diagram of minimum value of circumferential pressure coefficient under different slits

图7所示为不同开缝条件下边界层分离点位置θ。从图7可见：当相对缝宽较大时(s/d为 0.050，0.075和0.100)，在0°≤α≤10°条件下，前侧流体在高压下经缝隙射入圆柱后侧流动滞止区，旋涡分离点位置明显后移；当 10°≤α≤30°时，分离点移动幅度较小；当 30°≤α≤80°时，随着开缝角度增大，圆柱前后侧压力差持续减小，动能增加，因此，流体能够克服更大的黏性力，分离点继续后移；当α=90°时，边界层吸吹作用趋于稳定，而缝隙对前后流场的沟通作用已经消失，分离点位置有所前移；当相对缝宽较小时(s/d为 0.005和 0.025)，分离点位置移动趋势与相对缝宽较大时相同，但因缝隙较窄，对流场影响较小。以往研究者普遍认为层流范围内圆柱绕流旋涡分离角小于90°，但近年来研究者通过实验和数值模拟的方法证明当Re数小于200时，旋涡分离角大于90°[27]，本文模拟结果也证明了这一结论。然而，PENG等[16]通过可视化实验现象发现当雷诺数较高(2 400≤Re≤11 400)时，随着相对缝宽增大，分离点位置随之前移。

3.3 升力和阻力

图8所示为不同开缝条件下前、后驻点的压力差。从图8可见：在0°≤α≤10°时，前、后驻点压力差随开缝角增大而增大，前驻点作为整个流场压力最大的点，其与后驻点的沟通大大降低了前后驻点的压力差；当倾斜角继续增加时，缝隙沟通作用减弱，前后驻点压力差增大；当 10°≤α≤90°时，前、后驻点压力差随开缝角增大而减小。前、后驻点压力差在一定程度上反映了开缝圆柱附近流场的压力分布，其值对圆柱所受阻力产生重要影响。

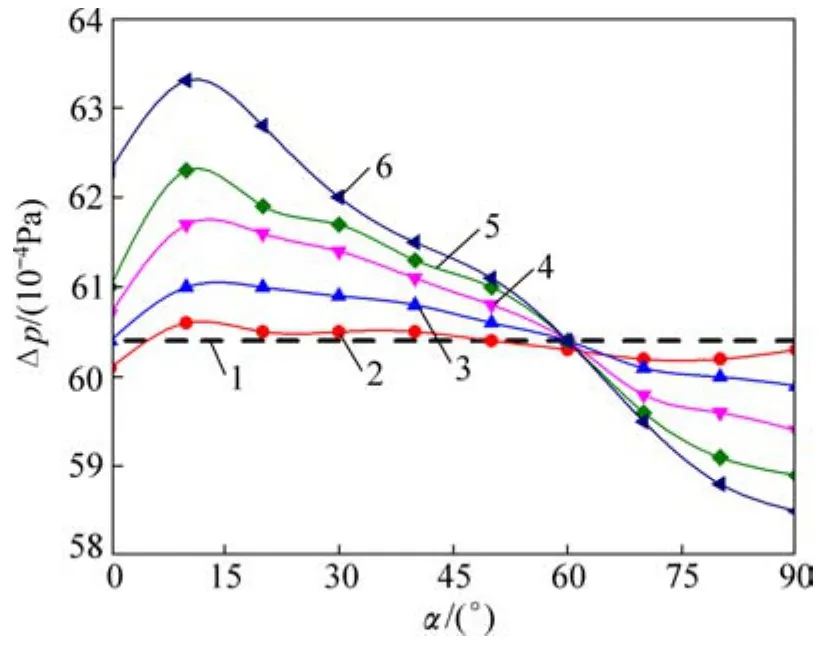
图8 不同开缝条件下前后驻点压力差ΔpFig.8 Pressure difference at front and back stagnation point under different slit conditions

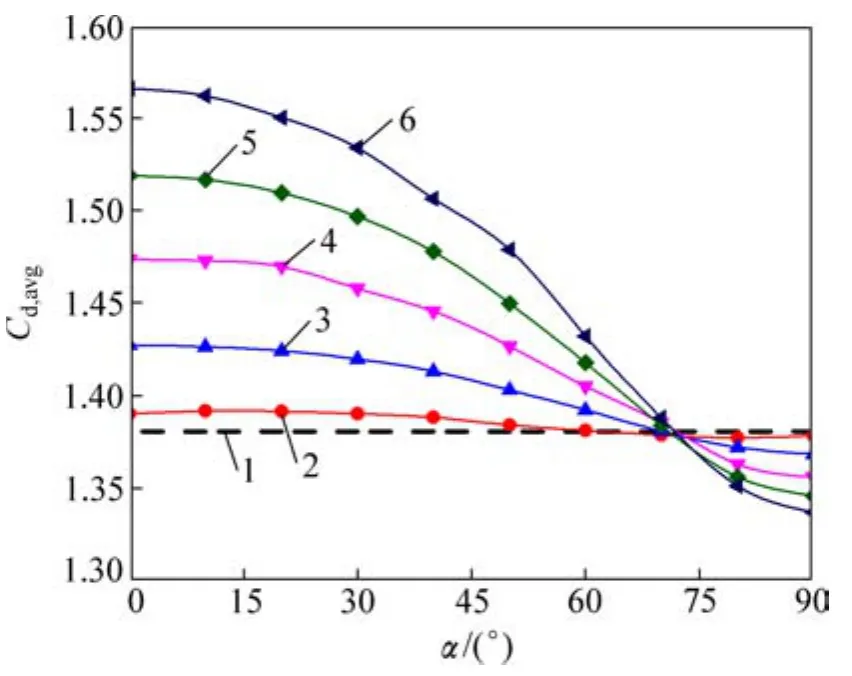
图9 不同开缝条件下圆柱时均阻力系数Cd,avgFig.9 Coefficient of resistance of cylinders under different slit conditions

图9所示为不同开缝条件下圆柱时均阻力系数。由于圆柱所受阻力由压差阻力和黏性阻力组成，层流条件下圆周上所受黏性阻力较稳定，其受开缝影响较小，而且缝隙两侧压差阻力较小，因此，开缝圆柱所受阻力主要由圆周所受压差阻力和缝内黏性阻力所决定。随着开缝角增大，缝隙过流量逐渐较小，其所受黏性阻力也逐渐减小。综合前、后驻点压力差可知：当0°≤α≤30°时，圆周所受压差阻力增加量小于缝隙黏性阻力减少量，开缝圆柱所受阻力减小；当30°≤α≤90°时，圆柱所受压差和缝内黏性阻力均减小时，开缝圆柱所受阻力随之减小。此外，从图9还可以看出：当α≤70°且其值不变时，随着相对缝宽增大，阻力系数不断增大；而当 70°≤α≤90°时，阻力系数变化趋势则相反。这与一定范围内随着相对缝宽增大，边界层吸吹作用增强、旋涡脱落频率增大有关，其值与未开缝圆柱的阻力系数的相对大小关系也可为圆柱绕流减阻提供参考。可见：随着相对开缝角度增大，圆柱所受阻力不断减小，且相对缝宽越大，圆柱所受阻力减小幅度越大；当s/d=0.1时，阻力系数减小14.63%。这与 IGARASHI[10]得出的“随着开缝角度增大，阻力系数随之增大”规律不同。这是因为当雷诺数较高时，自引入现象和边界层吸吹作用占主导地位，阻力系数随着开缝角增大而逐渐增大，且当边界层分离位置位于开缝前端时，其值达到最大。

图 10所示为不同开缝条件下圆柱均方根升力系数。从图 10可见：在固定相对缝宽条件下，当0°≤α≤30°时，升力系数随开缝角度的增大不断增大；当 30°≤α≤90°时，升力系数随开缝角的增大不断减小。这是因为当0°≤α≤30°且开缝角不断增加时，缝隙出口低压区拉动圆柱后部低压区向圆柱下侧移动，造成圆柱上下侧压差增大，升力随之增大；当开缝角继续增大时，缝隙出口低压区与圆柱后侧低压区断裂，继而汇入圆柱下侧肩部低压区，缝隙对上下侧流场的沟通作用造成圆柱上下侧压力差较小，升力随之减小。

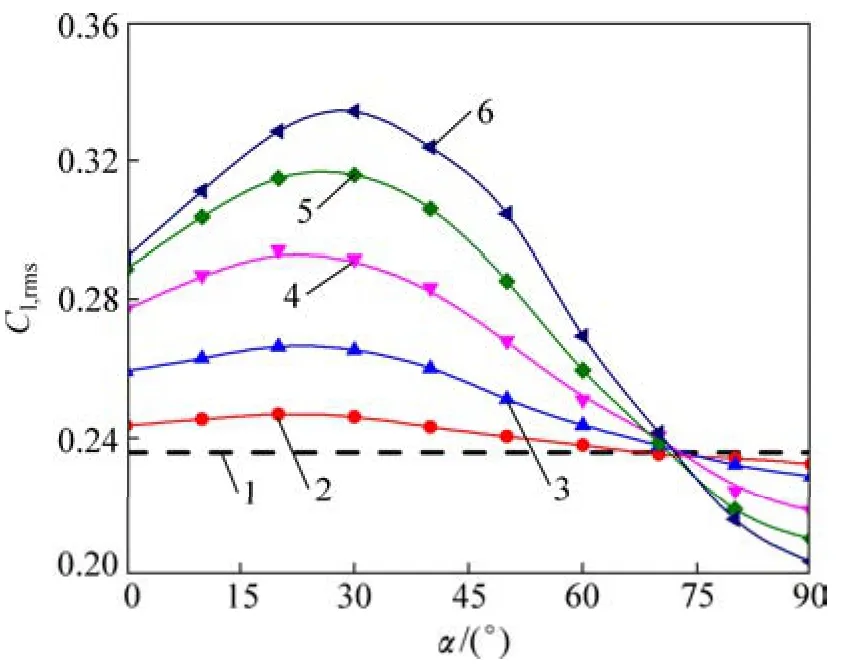
图10 不同开缝条件下圆柱均方根升力系数Cl,rmsFig.10 Lift coefficient of column root mean square under different slit conditions

3.4 旋涡脱落频率

图11所示为不同开缝条件下的斯特劳哈尔数St。从图11可见：在相对缝宽较小时(s/d取0.005，0.025和 0.050)，随着开缝角增大，旋涡脱落频率在波动中有所增大且均比未开缝圆柱的大；在相对缝宽较大时(s/d取0.075和0.100)，随开缝角增大，旋涡脱落频率增幅较大，其值仅在开缝角α大于70°时才比未开缝圆柱的略大，这验证了增大开缝角度可以在一定程度上增大旋涡脱落频率的规律，但也揭示了这一规律的局限性，即该规律仅对一定范围内较大相对缝宽的圆柱较明显；而当雷诺数较高时，St在开缝角较小时保持不变，或者略减小；当开缝角大于 50°时才会随着开缝角增大而增大[11]。

图11 不同开缝条件下的斯特劳哈尔数StFig.11 Strouhal number under different slit conditions

3.5 缝内流动

为了进一步揭示开缝对圆柱绕流尾迹流场的影响，对缝内流体速度及所受升阻力进行计算。图 12所示为不同开缝条件下缝内流体时均速度U。从图12可见：随着开缝角增大或相对缝宽减小，缝内流体流动速度持续减小。这是因为随着开缝角增大，缝隙进出口压力差逐渐减小。

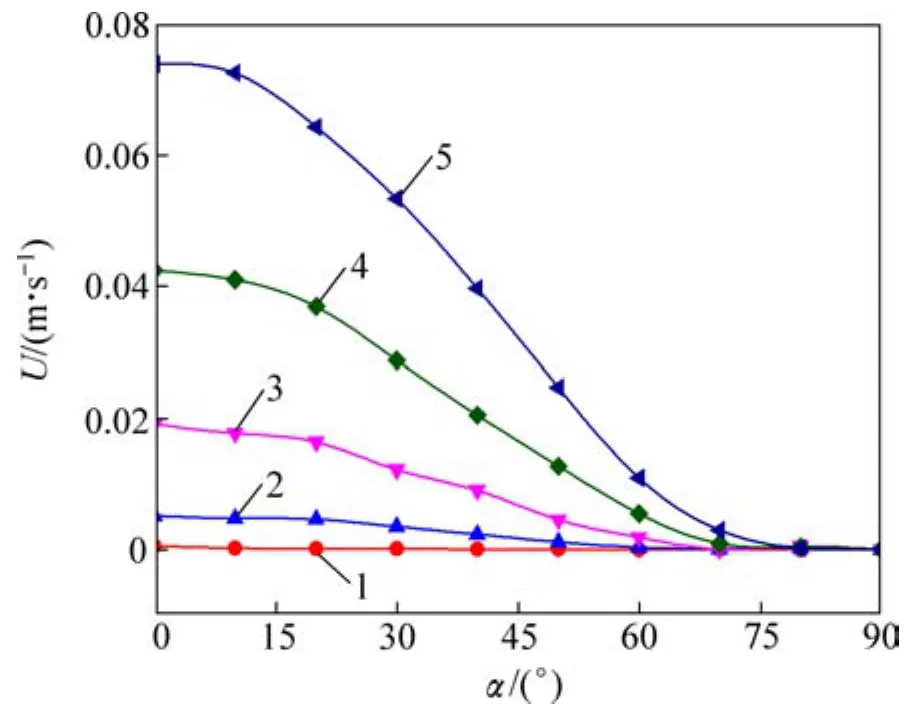
图12 不同开缝条件下缝内流体流速UFig.12 Fluid velocity in slit under different slit conditions

图13 不同开缝条件下缝内流体特征参数Fig.13 Parameters of fluid in slit under different slit conditions

图 13(a)所示为不同开缝条件下缝内流体特征参数。由于缝隙两侧所受压力近似相同，所以，所受阻力主要由黏性阻力决定；随着开缝角度的增大，缝隙进出口处压差减小，过流量减小，因而所受阻力减小。图13(b)所示为缝隙所受升力变化情况。从图13(b)可见：当开缝角小于 40°时，随着开缝角度增大，缝隙所受升力逐渐增大。这是因为缝隙出口低压区与圆柱后侧低压区融为一体，增加了前后压差在垂直来流方向的分量；随着开缝角增大，这一效果更加明显；当40°≤α≤60°时，开缝出口低压区汇入圆柱下侧低压区，缝隙的沟通作用使得圆柱上下侧肩部压力差减小，因此，缝隙所受升力减小，并在α≥60°时保持不变。

4 结论

1)相对缝宽和开缝角对圆周压力整体分布影响不大。随着相对缝宽增加，圆周最小压力点位置后移，移动幅度随相对缝宽的增大而增大，当s/d=0.1时，其值达到最大(Δφ0=6.11°)。开缝角对边界层分离点影响较大：在 0°≤α≤10°时，分离点明显后移；在10°≤α≤80°范围内继续后移，但速度减缓；在80°≤α≤90°范围内，分离点稍有前移；在不同相对缝宽条件下，分离点位置随开缝角变化的趋势一致。

2)随着开缝角度增大，前后驻点压力差不断减小，圆柱所受阻力不断减小，且相对缝宽越大圆柱所受阻力减小幅度越大。当s/d=0.1时，阻力系数减小14.63%。在0°≤α≤40°范围内，圆柱所受升力系数不断增大，40°≤α≤90°范围内呈减小趋势。随着开缝角增大，旋涡脱落频率均增大，在相对缝宽较大时，该规律更明显。

3)随着开缝角增大，缝内流体流动速度和缝隙所受阻力逐渐减小，缝隙所受升力则先增加后减小，最后保持不变。