基于CRLB的舰炮定位精度能力需求生成

许俊飞，王航宇，卢发兴，吴 玲

（海军工程大学兵器工程学院，武汉 430033）

0 引言

为适应未来海战场环境及作战需求，新型舰炮已发展成为具有高初速、远射程和快速打击等优越战技性能的杀伤武器，舰炮武器系统对目标的精准定位是把握战场态势、指挥决策和精确打击的重要前提，如何根据作战态势提出对目标定位精度要求是亟待解决的现实问题。舰炮定位精度是指雷达系统对目标的定位能力，定位精度作战能力需求生成是指在作战过程中为有效完成各项作战任务，即新型舰炮要达到一定的命中概率时，对目标定位精度的量化要求。

目前针对目标定位精度的研究有很多[1-2]，但多只针对雷达装备本身或算法研究，并没有根据作战目的对定位精度进行量化求解。本文针对舰炮对海作战任务，利用克莱默下界（CRLB）理论推导由目标定位精度引起的命中点预测误差计算模型，即火控系统误差，以单发命中概率模型为牵引，建立舰炮对海作战过程中的随机误差、射击命中界、检测概率、火控处理时间等模型，重点分析为达到指定作战目标时，对目标定位精度能力的解析关系，定量生成舰炮对目标定位精度的能力指标需求，为新型舰炮配套系统雷达装备的论证与发展提供依据。

1 需求生成框架

对海射击时影响单发命中概率的误差源可以分为系统误差与随机误差两大类[3]，系统误差主要是由火控设备对于目标的定位而引起的误差；随机误差主要是由多方面不确定因素引起的，因此，本文可从建立舰炮对海射击过程中要达到的射击概率入手，建立影响单发命中概率的因素模型，对所需的目标定位精度进行反推，求解框架模型如图1所示。

1）利用Cramer-Rao下界理论，推导在目标定位精度影响下的火控系统误差模型，根据求解需求还需建立对目标的检测概率模型、火控处理反应时间模型；

2）建立舰炮射击密集度模型，求解不同射击距离下的射击密集度和舰炮射击命中界；

3）根据作战对单发命中概率的要求对目标定位精度进行求解。

2 模型建立

2.1 系统误差模型

2.1.1 CRLB下的火控系统误差

火控系统误差主要表现为对目标命中点位置预测误差，由目标定位精度、火控滤波时间、数据采样间隔、预测时间等因素综合影响[4]。CRLB是对跟踪问题的有意义的评价，它表示任一无偏估计的误差下限或精度上限，在对海射击过程中，设目标在X轴方向为匀速直线运动，其测量方程为

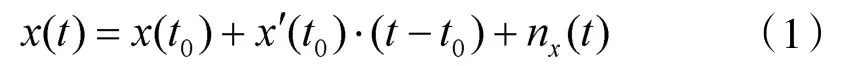
一般令t0=0，式（1）可表示为矩阵形式

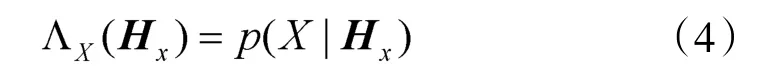
因此，

由于

所以

假设雷达对目标定位的距离精度为σrr，方位精度为σrθ，因此，雷达对目标定位在提前点引起的线误差σx与方位误差σz为

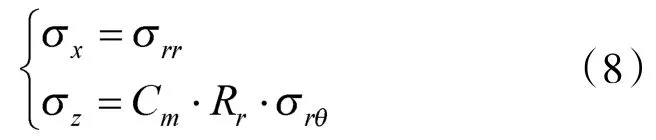
式中，Cm为密位变为弧度的转换系数；Rr为射击的水平距离。

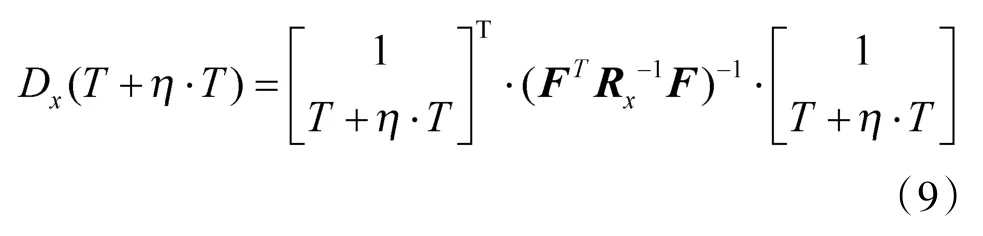
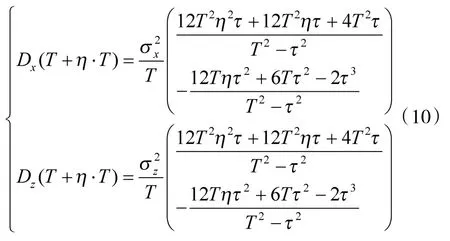
对海射击过程中的系统误差可认为主要由火控系统误差决定，因此，系统误差mx、mz可取为目标运动要素估计误差的精度下限CRLB，由上式可知：

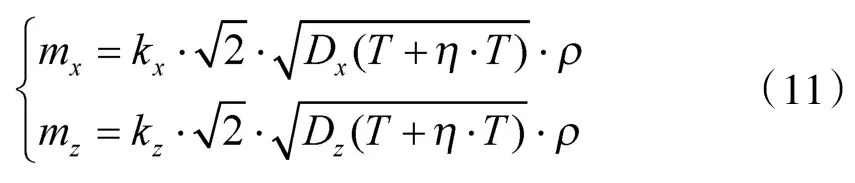
式中，kx，kz为系统误差系数，一般取；ρ 为正态常数，ρ=0.476 9。

2.1.2 火控处理时间

在火控系统误差的建模过程中，滤波时间为T，火控处理过程基本上就是滤波的过程，处理时间主要取决于点迹形成航迹的滤波方法，而在所有的滤波方法中，最小二乘滤波是适用性最强的滤波方法，位置滤波均方误差和一步外推均方误差公式为[6]：

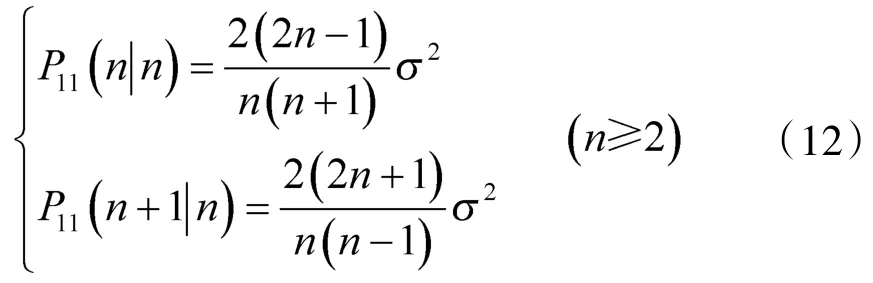
式中，n为采样点数；σ为量测的常数均方根误差。

式（12）是估算公式的主项，在此基础上考察目标检测概率Pdr和目标速度vm（马赫数）对位置滤波、外推误差的影响关系：

式中，α、β为修正系数，经优化确定取值α=1/3、β=1/2。

在计算过程中，通常会取一个与过程精度要求相关的值，即误差压缩系数的要求值2，该变量描述了系统的精度，满足的n值则为给定系统精度的采样点数[7]。

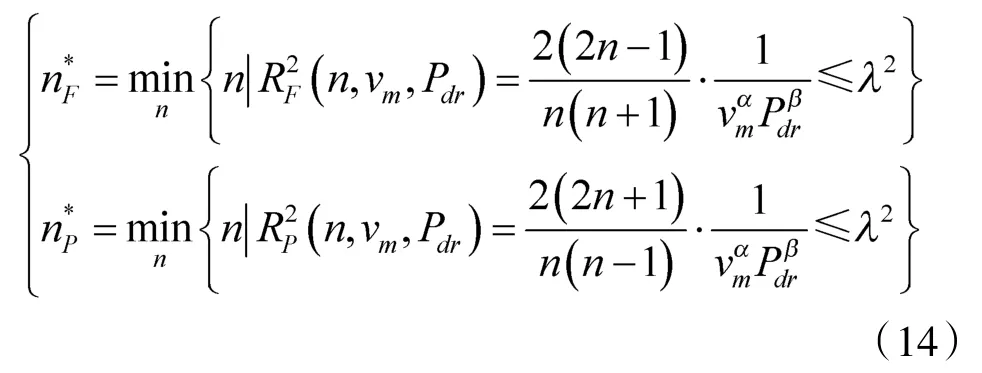
因此，火控系统滤波时间T为

2.1.3 检测概率

一般雷达部署确定以后，其本身固有的参数（如工作波长，发射频率）就随之确定，若其他环境参数（如气象条件、干扰状况等）及目标的参数也确定[8]，那么雷达所需信噪比与检测概率、虚警概率之间将满足

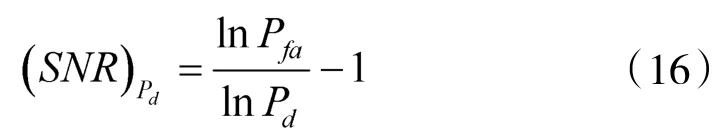
结合雷达方程，雷达雷达探测距离与检测概率、虚警概率之间的关系，进行恒等变换，将其转化为关于检测概率的一个赋值表达式，获得不同距离的雷达检测概率计算模型[9]

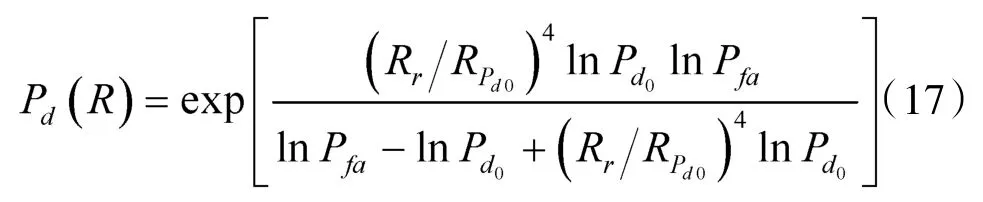
式中，RPd0表示在约束检测概率为Pd0时雷达的最大探测范围，当雷达的探测距离等于雷达的最大探测距离时，雷达的检测概率为0.5[10]，因此，计算时取Pd0=0.5；Pfa为虚警概率，一般取 10-6。

2.2 随机误差模型

在舰炮射击过程中，随机误差主要体现为舰炮的散布误差、随动系统误差以及弹道气象准备误差，由于弹道气象准备误差形成的射击准备综合精度与其准备的方法及技术水平密切相关，可通过前期的射击准备予以消除，本文暂且将弹道气象准备误差忽略不计。

在使用单炮对海射击时，按照海军习惯将由舰炮随动系统误差和射弹散布误差的合成称为舰炮单炮散布误差，而射击密集度是指弹着点相对散布中心的偏离程度，对于舰炮武器系统，射击密集度是以舰炮散布误差的大小来衡量，即以其距离方向概率误差来表征，因此，可用射击密集度来表征系统的随机误差[11]。

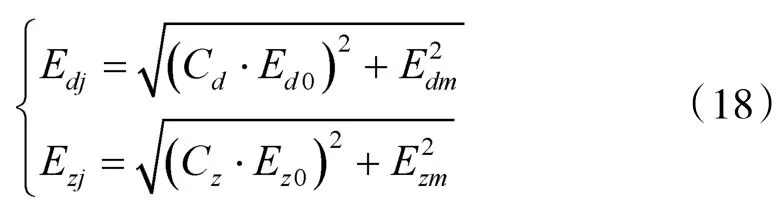
式中，Cd、Cz为舰炮散布修正系数，为射弹散布误差；Edm和Ezm为舰炮随动系统误差。

由于射弹散布误差与随动系统误差的取值大小与水平射击距离相关，因此，随机误差可通过以下简化公式进行仿真计算：

式中，ηx、ηz分别为距离和方向射击密集度系数；Cm为密位变为弧度的转换系数，Cm=1/955。

2.3 命中界模型

海上目标命中面积是弹丸可击中的目标面积，一般可根据等面积替代原则，用规则形状的目标面积近似代替舰艇命中面积[14]。以水面舰艇为例，设目标舰艇甲板面等效矩形长为Lj，宽为Bj，舰艇平均舷高为Hp，根据面积等效原则，当弹丸落角θc极小时，应将舰艇命中面积投影在弹丸落速的垂直面上，因此，舰艇目标的命中界模型为

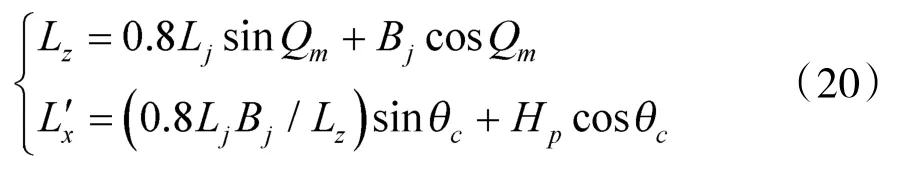
式中，Lz为舰艇目标的方向命中界，Lx为舰艇目标的距离命中界，θc为弹丸落角，可通过外弹道模型求解得到。

舰艇命中界不但与舰艇的外形特征有关，而且还与目标舷角和落角有关。在其他条件相同情况下，当Qm=90°时，可认为舰艇命中面积为最大，当θc增大，即射击距离增大时，舰艇命中面积将减小。

2.4 单发命中概率模型

单发命中概率的大小主要取决于射击误差的分布特性和目标的外形特征，通过上述系统误差、随机误差以及命中界模型的建立，可以得到系统误差为 mx、mz，射击误差的概率误差为 Ex、Ez，对于海上舰艇目标，一般近似处理为矩形目标，根据命中界模型，设矩形目标的边长为2Lx和2Lz，对此矩形目标射击的单发命中概率为

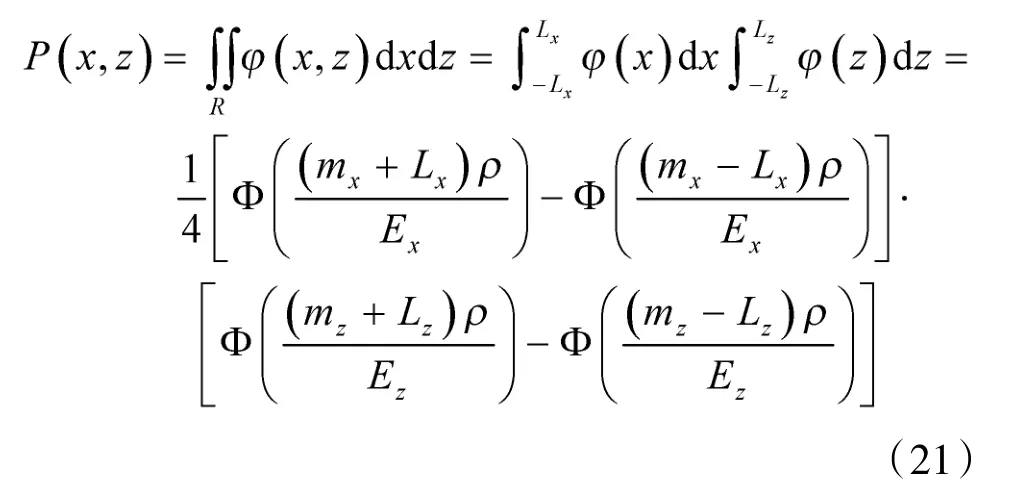
3 仿真分析

新型舰炮对于未来海上火力支援作战具有重要的意义，当前我方面临的海上典型目标以美军的阿利伯克级驱逐舰为主。由定位精度、火控滤波时间等因素造成的火控系统误差解析计算比较复杂，通过单发命中概率的解析计算公式很难反推出定位精度值，因此，在求解过程中，采用遍历求解的方法，当计算得到的命中概率与所要求的命中概率差值在可容许的阈值内，即满足要求，求解过程如图2所示。

拟定作战想定：作战环境适宜，敌方舰艇在距我方一定距离外，Rr以目标航路角30°向我方袭来，我方使用新型舰炮对其进行打击。

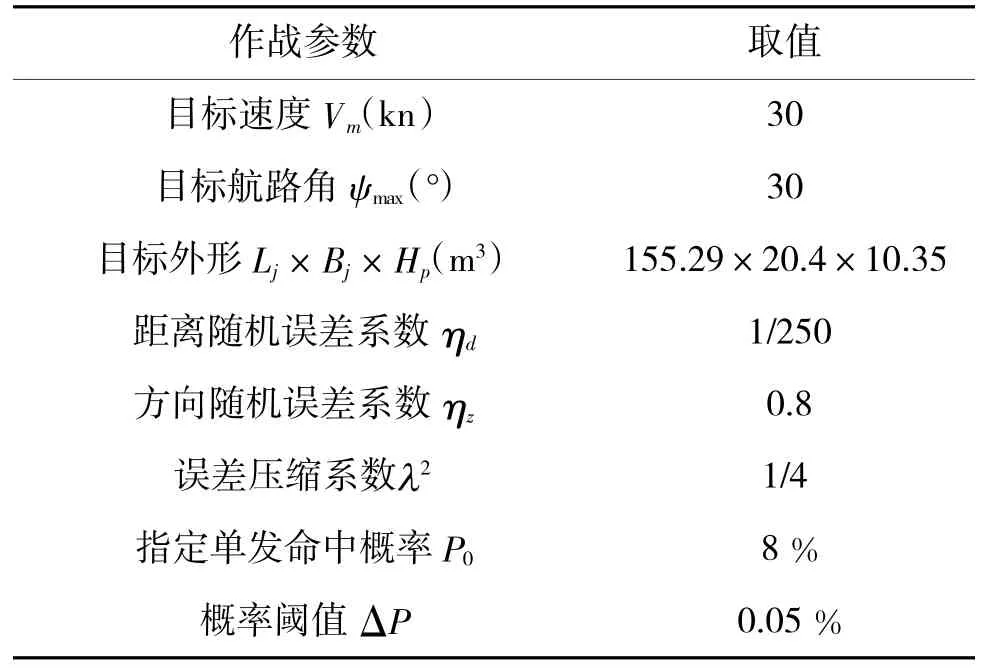
表1 作战参数值

3.1 射击距离不同对定位精度的要求

在仿真计算时，取弹丸初速为vw=2 000 m/s，得到在不同距离情况下，当指定单发命中概率达到8%时对目标的定位精度要求。对海目标定位精度指标由距离精度与方位精度组成，当取距离精度分别为40 m、60 m、80 m时，求取相对应的最低方位精度，仿真结果如表2所示。

表2 命中概率为8%下固定距离精度所需的最小方位精度

当取方位精度分别为0.2°、0.3°、0.4°时，求取相对应的最低距离精度，仿真结果如表3所示。

从表2和表3中可以看出：

1）当射击距离一定时，对目标定位的距离精度提高时，方位精度变化很小，当对距离精度要求较高时，方位精度要求则会相应减小，反之亦然；

2）随着射击距离的增大，为达到指定的射击概率，对定位精度的要求在不断提高，当提高到一定程度时，随着射击距离的增大，定位精度无法满足要求使其射击概率达到指定值。

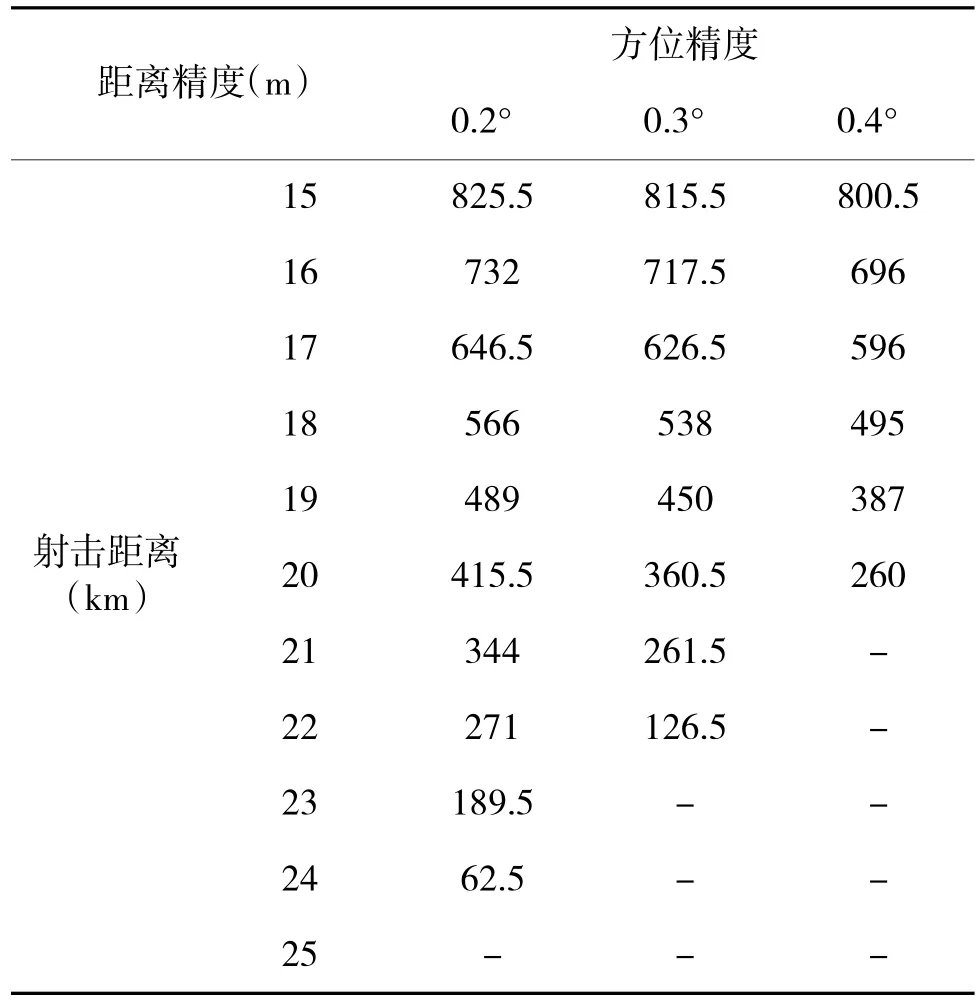
表3 命中概率为8%下固定方位精度所需的最小距离精度

如表2，在弹丸初速为2 000 m/s时，如果某型雷达对目标的定位精度为（60 m，0.3°），则当射击距离大于22 km时，系统精度便无法满足要求使其射击概率达到8%，如果可以通过技术手段提高，那么在23 km～27 km仍可满足单发命中概率达到8%的要求，但当射击距离超过27 km时，定位精度的提高已不能满足单发命中概率达到8%的要求。

3）当目标定位的方位精度相对固定时，随着射击距离的增大，为达到指定的命中概率，对距离精度的要求越来越大，说明方位精度的变化对命中概率的影响较大。

如表3，当方位精度为0.3°时，从仿真数值中可以看出，当射击距离为22 km时，只要距离精度达到126.5 m的要求，单发命中概率即可达到8%，而当射击距离大于22 km时，无论距离精度如何提高都无法满足要求，因此，方位精度相比距离精度对命中概率的影响更为显著一些。

3.2 速度不同对定位精度的要求

当速度固定时，超过一定的射击距离，便无法达到指定射击概率的作战需求，新型舰炮的特点在于其初速可调，现讨论不同初速对射击距离以及单发命中概率的影响关系，以初速为1500m/s，2000 m/s，2 500 m/s为例进行分析，结果如下页表4和表5所示。

从以上仿真数据中可以得到：

1）距离精度一定时，随着射击距离的增大要达到指定的命中概率，对方位精度要求越来越高；射击距离一定，初速越小，对方位精度的要求越高，反之同理；

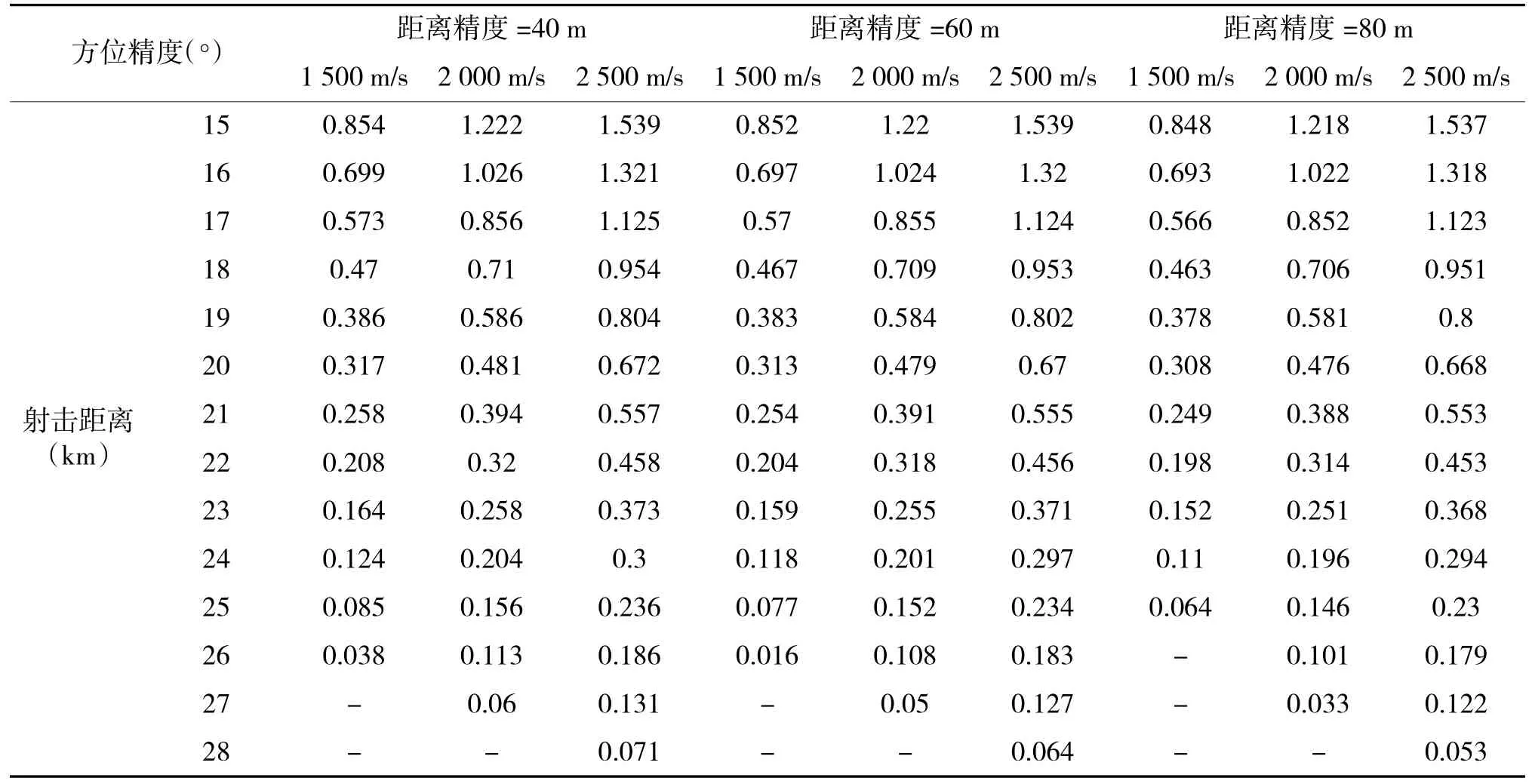
表4 固定距离精度不同初速不同射击距离下所需的最小方位精度

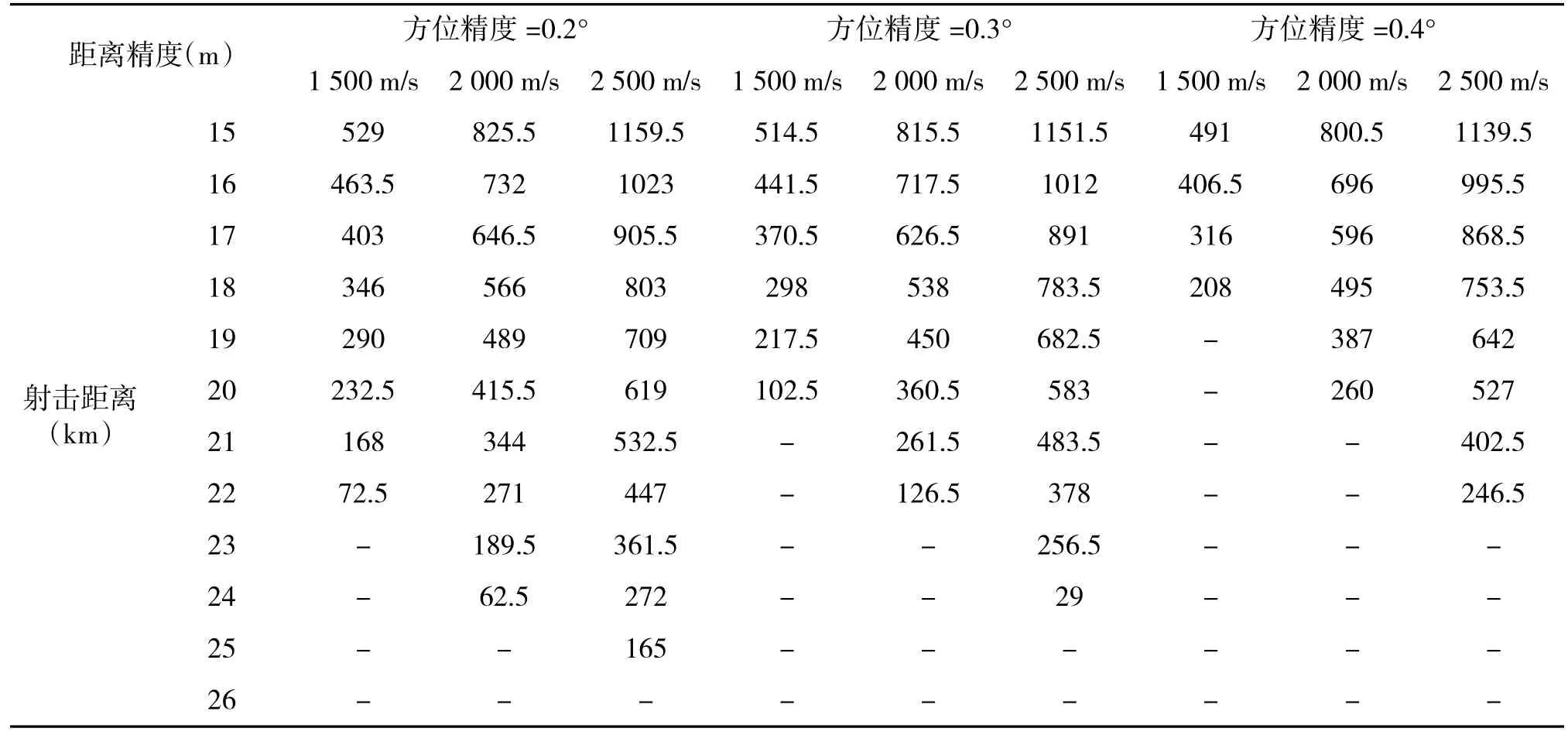
表5 固定方位精度不同初速不同射击距离下所需的最小距离精度

图3 距离精度为60 m下不同射击距离所需的最小方位精度

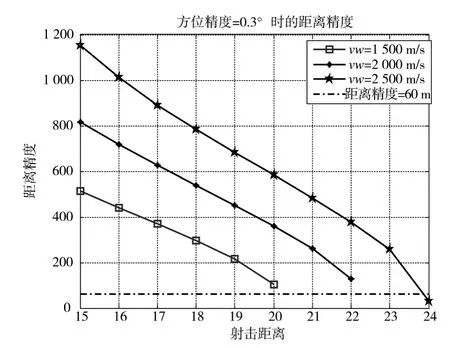
图4 方位精度为0.3°下不同射击距离所需的最小距离精度

2）当对目标的定位精度水平一定时，舰炮武器系统的初速越大，越能在更远的射击距离上达到指定命中概率。

根据表4及图3，如果不考虑技术水平的发展即方位精度可以达到很高，以距离精度为60 m为例，初速为 1 500 m/s、2 000 m/s、2 500 m/s时对应的方位精度为0.016°、0.05°、0.064°，大于26 km、27 km、28 km后无法满足单发命中概率为8%的要求；由于技术水平的限制，方位精度不可能无限高，某型雷达方位定为精度为0.3°时，从图5可以看出，初速越大可在更远的射击距离上满足单发命中概率为8%的射击要求，如图3所示，当距离精度为60 m，初速为1 500 m/s时最大射击距离为20 km，而2 500 m/s可达到24 km。

根据表5及图4，以方位精度为0.3°为例，初速为 1 500 m/s、2 000 m/s、2 500 m/s时对应的距离精度最小要求为102.5 m、126.5 m、29 m，大于20 km、22 km、24 km后无法满足单发命中概率为8%的要求；限于装备技术水平的发展，某型雷达距离定位精度最高为60 m时，从图4可以看出，当方位精度为0.3°，初速为1 500 m/s时最大射击距离为20 km，而初速为2 500 m/s在24 km处无法满足要求，要小于24 km。

4 结论

本文以舰炮对海上目标的命中概率模型为牵引，建立基于CRLB定位精度影响下的火控系统误差模型、射击密集度模型、弹丸外弹道模型，以及射击命中界模型，仿真分析了为达到作战要求的指定命中概率对目标定位精度的作战能力需求，通过分析可得，在初速、射击距离确定的情况下，为达到指定的命中概率对目标定位精度提出的最低要求，同时目标定位精度的提高可以使射击距离更远，由于技术发展水平的限制，可从降低舰炮随机误差，如射弹散布等方面进行提高，也可提高弹丸初速以达到指定命中概率的要求。