武器-目标分配问题研究*

2019-06-13杨进帅

火力与指挥控制 2019年5期

杨进帅，李进，王毅

（空军工程大学防空反导学院，西安 710051）

0 引言

武器-目标分配[1]（Weapon-Target Assignment，WTA）问题是研究分配武器单元打击敌方目标，从而取得最佳打击效果，优化火力打击体系，也称目标分配或者火力分配。是现代战争中指挥控制的关键问题之一。制定合理的火力分配方案，可以优化资源配置，用最小代价获取最大战场收益[2]。WTA问题实质是一类非线性组合优化决策问题，解空间大小随着武器和目标数量的增加而呈指数增加，是一个NP完全问题。

WTA主要在两个方面进行学术研究，一是模型研究，旨在建立更为合理、贴切实际的模型；二是算法研究，快速有效解决WTA问题，给出分配方案以提供决策支持。

1 基本内容

WTA问题的研究目的是提高战场指挥控制的自动化水平，快速有效地解决大规模武器目标的分配问题。武器-目标分配问题的研究可以追溯到上世纪五六十年代，最初的研究目的是用于制定作战计划、指挥军官训练，提高作战指挥的能力，为武器的选择以及新武器的研制与采购提供参考，而不是直接用于战场的作战指挥。

1.1 WTA分类

根据目标威胁和对抗方式可以划分出多种WTA类型，如图1所示。

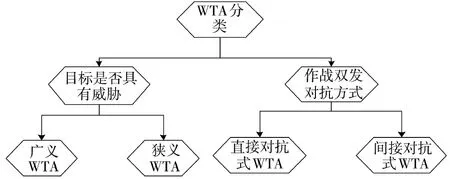
图1 WTA分类

考虑目标威胁，武器-目标分配问题划分为狭义WTA和广义WTA，狭义WTA中目标一定有威胁，而广义WTA中目标可能有威胁，也可能没有威胁[3-4]。考虑作战双方的对抗方式，武器-目标分配问题分为直接对抗式WTA和间接对抗式WTA。其中直接对抗式WTA的目的是消灭敌方，以此来进行目标分配，目标打击对象是防御方的武器；间接式WTA又称资源防护型WTA，是防御方保护资源不受摧毁或损失最小，选择性地对敌人的目标进行打击，目标打击对象是防御方所保护的资源。

1.2 WTA问题性质与数学模型

武器-目标分配问题的数学描述为T个目标攻击W个武器平台，第i个武器平台被第j个目标毁伤概率是；其中第i个武器平台的重要性是wi，并且第i个武器平台可用于防御的武器有mi件，第j个目标被它的第k件武器毁伤概率是rikj。同时，最多使用W个武器平台上的nj件武器对第j个目标进行还击。确定武器-目标分配方案是WTA求解的目标，最终目的是使己方损失最小。xikj=1表示第i个武器平台的第k件武器对第j个目标进行还击，否则xikj=0。

武器-目标分配问题的数学模型[4-5]抽象为如下形式：

在上述数学模型的基础上，不同的作战目的可以建立不同的WTA模型，既可以是单目标的，也可以是多目标的。多目标WTA可以通过权值转化为单目标WTA，也可以引入罚函数求解非劣解。

WTA问题一般具有下列数学性质：

1）WTA问题是NP完全问题；2）WTA问题具有离散性，难以进行微分；3）WTA问题具有随机性，需要用随机模型来描述武器与目标的交战活动；4）武器与目标的规模较大；5）目标函数是非线性的。

2 WTA问题研究现状

2.1 模型研究

模型研究主要分以下几个方面[3-4]：

1）模型假设。合理假设是建模研究的首要问题，WTA问题由于对抗环境的复杂性，必须合理抽象，建立准确模型才能有效解决WTA问题。

2）目标函数选择准则。不同的决策意图和不同的交战策略决定了不同的选择准则，一般可以采用防御方消耗最小、资源损失最小，敌方潜在威胁最小和敌方剩余目标数最小等选择准则设计目标函数。

3）约束条件；与决策意图有关，决定了问题的复杂程度，主要包括武器与目标的数量、毁伤概率、资源价值、目标威胁等因素。

4）时间因素。动态多变的战场环境对武器射击提出了时间的要求，不考虑时间因素的影响，不能正确反映实际作战过程。

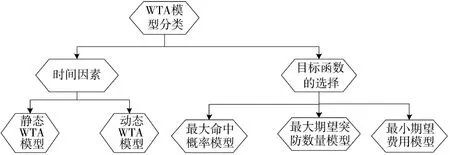
图2 WTA模型分类

因此，不同的出发点可以划分不同的WTA模型，如上页图2所示。静态WTA模型和动态WTA模型是国内外学者研究最多的两种模型。

静态WTA（SWTA）是基于所有武器同时分配发射和武器目标之间交战相互独立这两个假设[6]建立的模型。SWTA中武器和目标状态固定、参数恒定且已知，其目标是防御方根据进攻方的武器估计类型、预测点影响值，针对暂时防御任务，给出最优分配。

静态WTA模型是研究的主体，国外学者Patrick A Hosein和 Michael A[7-9]对一般性 WTA 问题进行了系统研究；S.P.Lloyd等[10]证明了WTA问题的NP完全性，指出其求解时间随问题规模的增加而指数增长；美军国防分析研究所改进了武器优化与资源需求模型[11]，并在C4ISR环境下建立了作战资源分配模型。国内学者主要针对特定领域进行研究，如空军工程大学的邢清华教授[12]等在防空导弹领域，装甲兵工程学院常天庆教授[13]等的坦克分队领域和国防科技大学蔡怀平教授[3]等。目前，基本解决了小规模的SWTA问题。

动态WTA（DWTA）模型是在SWTA模型的基础上，注重考虑分配过程中可能的随机事件并及时处理，研究动态防御作战过程中武器目标最优分配。由于时间因素和随机事件的影响，增加了问题求解的难度[14]。DWTA 的研究主要有 Hosein[15-16]的多级武器-目标分配和韩松臣[17]的基于马尔可夫决策过程最优化的动态WTA两种方法。

多级武器-目标分配将动态WTA问题分成许多时间段，是根据来袭目标持续的时间。在每个时间段中，根据目标当前情况，允许防御方发射武器进行迎击，而且所有武器效能评估由于前一阶段袭击过程中反馈信息的存在，防御方能更好地进行武器分配，提高武器的进攻效果。基于马尔可夫决策过程最优化的动态WTA方法结合动态分配策略和静态WTA模型，运用随机过程理论，为动态WTA提供了理论和方法依据[18]。

2.2 算法研究

求解SWTA的传统算法主要包括分枝定界法[19]、隐枚举法[20]、动态规划法[21]和割平面法，这些算法编程较为繁琐，难以处理大规模WTA问题。随着计算机技术的发展，一些启发式优化算法通过模拟自然现象或过程，为处理复杂问题提供新方法和新思路，比如遗传算法（GA）、粒子群算法（PSO）、蚁群算法（ACO）、差分进化算法（DE）等。

2.2.1 遗传算法求解WTA问题

遗传算法（GA）是 Holland教授[22]于 1975年提出，基于适者生存、优胜劣汰等自然进化规则模拟生物进化过程和基因遗传操作。遗传算法由于鲁棒性高、适应性强的特点在WTA问题中被广泛使用，取得了一定效果但也暴露出不少迭代时间长、过早收敛、容易陷入局部最优解和封闭竞争等局限和不足。鉴于此，国内外学者采用不同的方法手段改进遗传算法，用于求解WTA问题。

曹伟华[23]从问题编码、初始种群产生、遗传操作等方面给出了武器-目标分配问题的遗传算法详细设计，进而求解WTA问题。王玮[24]通过设计一种满足约束条件的染色体编码格式，把求解问题转化为无约束组合优化表现形式，利用精华选择策略、单点随机定位算术交叉和变异运算进行求解。杨山亮[25]采用精英选择和动态遗传算子改进遗传算法求解多种作战力量参战条件下的多武器-多目标的联合作战，避免了过早的收敛。常天庆[13]改进了基本遗传算法的关键步骤，设计了基于火力单元排序的战术种群初始化策略，在进化初期就产生适应度很高的个体，引入了小生境共享函数和参数自适应机制，维持种群的多样性的同时加速收敛，在坦克分队的武器-目标分配问题上取得了良好的收敛效果。薛羽[26]根据协同干扰武器-目标分配问题的实际性质，引入启发式规则，提出了具有贪婪修复过程的免疫遗传算法，求解大规模CJWTA问题，在较短时间内得到了较高质量的分配方案。吴坤鸿[27]设计了一种分布式遗传模拟退火算法，采用多目标分布式搜索方式，在交叉算子中引入模拟退火算法，保持算法的广度和深度搜索平衡，有效求解了火力打击目标分配的多目标优化问题。余家祥[28]改进了传统局部搜索遗传算法，将贪婪构造应用于局部搜索，设计了优秀保留交叉操作方法，获得了较好的搜索效率，并不改变算法的全局收敛速度。徐加强[29]从火力分配实时性角度出发，考虑常规导弹生存、突防等影响因素，以毁伤下界为约束，建立了时空约束的动态常规导弹火力分配模型，结合遗传算法和禁忌搜索的特点，构建了遗传禁忌融合算法，在较短时间内找到最优解。董朝阳[30]基于目标函数的相对大小构造火力分配的适应度函数，采用种群染色体相似度，灵活有针对性地对父代染色体进行交叉或变异操作，防止算法陷入局部最优同时保证更新速度，获得了高效的寻优能力。

2.2.2 粒子群算法求解WTA问题

近年来，国内外许多学者探索运用粒子群算法求解WTA问题，同遗传算法比较，粒子群算法[31]（PSO）没有许多参数需要调整，容易实现。

李欣然[32]提出了一种改进粒子群算法求解多种类型武器-目标分配问题，首先定义粒子聚焦距离变化率，自适应调整惯性权重；其次采用速度最大值线性递减的策略平衡算法收敛精度与全局寻优能力之间的矛盾；最后使用优势粒子替换劣势粒子的策略加快粒子收敛速度，使得算法适合求解各种大规模的武器-目标分配问题。提高武器-目标分配问题的求解效率和性能，曲在滨[33]提出了一种离散粒子群算法，重新定义了粒子群算法中的速度和位置，采用贪心的启发式策略调整迭代产生的方案，快速找到最优解或次优解。张蛟[34]采用混沌离散粒子群混合优化算法对以毁伤概率为优化目标，兼顾火力资源消耗的多次拦截时机的防空火力分配模型，提高了算法的全局搜索能力，避免陷入局部极值。范成礼[12]运用怀疑因子和斥力因子改进位置和速度更新公式，有效避免发生早熟收敛和陷入局部最优问题，同时保持了PSO固有的收敛速度，有效地处理大规模WTA问题，为现代战争进行实时性辅助决策。刘晓[26]通过化解约束条件、修改速度和位置更新改进多目标粒子群优化算法（MOPSO），使之适合求解WTA模型。刘爽英[36]提出了一种改进的量子粒子群优化算法，根据粒子聚集度来判断早熟停滞，并用慢函数克服，同时保持种群的多样性，能快速给出WTA的最优或近优分配方案。

2.2.3 蚁群算法求解WTA问题

蚁群算法易于与其他算法相结合，具有分布式、正反馈、鲁棒性好的优点和收敛速度较慢的缺点[37-38]。

袁梅[39]通过采用了信息素递减的信息素更新策略以及随机数方法的选择原则，明显加快解的收敛速度。崔莉莉[6]在蚁群算法信息素的更新规则中引入PS算法，利用局部搜索经验和去哪聚搜索经验指导后继粒子搜索的机制，扩展搜索空间，增强蚂蚁局部搜索经验和群体全局搜索经验，提高收敛效率。黄国锐[20]运用多目标模糊优选理论建立最佳武器-目标分配模型，采用蚁群算法对分配模型转化为蚁群网络进行求解。仿真结果表明，相同的弹药消耗量、射击效果和群体规模下，蚁群算法的收敛速度和最优解的性能优于其他算法。武从猛[40]在求解大型水面舰艇编队防空的武器-目标分配问题时，将遗传算法融入蚁群算法，运用遗传算法的全局随机搜索能力生成一组粗略解，用其作为蚁群算法的初始信息素，运用蚁群算法的并行性、正反馈机制，发挥了遗传算法和蚁群算法的优点，在最短时间内获得了最优火力分配方案，缩短了武器反应时间。苏淼[41]等人利用免疫记忆和克隆选择的思想方法，引入记忆库，提出了基于免疫记忆的蚁群算法，通过进行给定数据集和随机数据集的WTA问题的实验，结果在不管是解的质量上和时间性能上均取得了较好的效果。

2.2.4 差分进化算法求解WTA问题

差分进化（DE）算法通过个体间的竞争与合作求解高维非线性优化问题[42-43]，实现简单、搜索能力强，但存在容易陷入局部最优、收敛速度慢等问题。

北京理工大学的张春美博士[44]，设计了离散差分进化算法的差分变异算子和交叉策略，提出了一种新的算法DDE-MRR，求解静态WTA问题，并与DDE-FBT和DDE-RPI算法进行比较，表明算法更容易求出最优解且收敛性能较好。王少蕾[45]针对水面舰艇编队防空反导作战中武器-目标分配问题模型，采取使种群个体满足约束条件的编码方式，利用混沌序列初始化种群，加强种群的搜索多样性，优化改进变异、交叉的动态自适应策略和混沌序列扰动，避免算法陷入局部最优，便捷地解决了多平台多类型武器-目标分配问题。梅海涛[46]运用算子K调节差分进化算法前后的变异率，增强全局和局部寻优能力，运用直觉模糊知识优化WTA模型。

2.2.5 其他智能优化算法求解WTA问题

许多新型智能算法也在求解WTA问题中尝试应用，从不同的角度出发，解决不同求解目标的WTA问题。

类电磁算法[47]将种群中的个体模拟为带电粒子，通过吸引和排斥作用引导个体朝最优解方向移动，全局搜索能力强，初步应用于项目调度和函数优化等领域。杨晓凌[48]改造原始类电磁算法的种群初始化、局部搜索、合力计算及粒子移动等步骤，使之适应武器目标问题的整数解空间。徐克虎[49]提出了一种“（1+λ）选择”的全局更新技术和Memetic局部更新技术的人工免疫算法，采用最优抗体抑制技术避免AIA陷入局部最优，具有较宽的收敛速度和精度。王邑[50]根据从已知决策中推理生成新的决策，减少重复搜索的思路，利用分支界限法得到分配方案的训练样本，通过构造并行运行的类型2区间模糊K近邻分类器的机器学习方法推导目标分配方案，实现快速决策。

2.3 不足及发展方向

国内外学者从模型抽象和求解算法等角度，对WTA问题进行了许多研究探索，取得了一定的效果，但仍然存在4个不足：1）主要集中在静态模型的研究，对动态WTA模型研究不够充分；2）动态与静态分配结合的研究比较少；3）尚未提出能应用于实际作战中的大规模WTA问题的有效算法；4）不确定因素的研究较少。

新军事技术的变革使战争形式发生了巨大变化，比如无人机、弹道导弹、高超音速飞机等，传统的WTA问题模型的适用范围大大缩小，但要求更为严格，要求时间更快、打击目标更准，这给敌我双方带来挑战和机遇。许多学者已经开始WTA模型的更深一步研究，有的学者以实施一体化联合作战[51-52]为战争主要形式，研究多军兵种的多种战术类型和多种装备型号防空武器的混合部署条件下，如何进行防空目标的优化分配等问题进行探索；有的学者运用模糊数学[53]和关系算子[54]改进模型，将WTA转化为无约束优化问题，获得了更多打击效率满意的目标。

WTA的算法研究主要集中于智能算法，且都认为自己的方法具有不错的收敛性，其实只要初始条件发生改变，则算法可能就不收敛。实际作战中这是致命的且不被允许的，必须在保证有解的基础上，提高求解的质量和速度。目前主要解决了规模较小的静态WTA问题，求解大规模动态WTA问题的算法速度较慢，尚未提出有效的算法。为满足军事技术发展的需要，解决大规模动态WTA问题显得尤为突出和重要。智能算法求解了WTA问题，较为有效地解决了时间和收敛性的问题，且混合智能算法策略也越来越显示出其有效性。可以说，求解大规模动态WTA问题，多种群智能算法的融合是此类优化问题的研究方向。

从现有文献看，求解WTA问题的智能算法层出不穷，需要统一的标准评价算法的寻优能力，寻找相对更高精度、更高效率的算法[55]。这一方面的理论研究相对较少，目前只有黄大山等学者从算法代码编制质量、算法精准度和算法执行效率3个方面对智能算法的寻优能力深入讨论，试图建立评价准则体系。建立完善的智能算法求解WTA问题评价准则体系，有利于针对不同类型的WTA问题选择合适的智能算法，在理论上有更为清晰的指导。