基于故障率的舰艇维修备品备件优化配置*

2019-06-13张怀强卢远超

火力与指挥控制 2019年5期

张怀强，卢远超，王孟

（海军工程大学，武汉 430033）

0 引言

现代海战往往具有持续高强度的特点，对舰艇装备保障率提出了较高的要求[1]。通过战时备品备件资源的科学配置，提升舰艇装备保障率，增强装备可靠性，对保障舰艇执行高强度作战任务具有重要意义。传统的基于经验的备品备件资源配置方案，虽然一定程度上保障了舰艇装备的基本可用，但配置方式较为粗放，难以适应高强度作战任务对于保障装备可靠性的需求，迫切需要探索一种面向装备保障率提升的舰艇维修备品备件资源优化配置方法。

本文针对上述问题，分析了不同备品备件故障率分布特点，建立舰艇装备保障率计算模型和备品备件保障费用约束模型，并根据作战任务特点进行多目标决策，对提升舰艇装备保障率，增强装备可靠性，保障舰艇作战任务的执行具有重要意义。

1 多目标模糊决策的基本理论

多目标模糊决策是由哈佛大学Zadeh教授提出的“模糊优化”理论的发展和延伸[2]。其基本理论为，在多目标优化决策模型中，多个优化目标之间经常存在强烈的冲突，造成某些目标的优化结果不能尽如人意。通常情况下，为了缓和这种冲突、兼顾所有目标的利益，决策者可以根据实际决策环境，提前给每个目标函数设定一个期望值，每个目标期望值都要等于或劣于其目标函数在系统约束下的最优值，进而根据目标取值的上限和下限分别建立决策满意度函数，并根据目标特点对满意度函数赋以权重，求得总满意度最高的决策方案[3]。

一般来说，优化目标分为最大化期望和最小化期望两种，决策者对优化目标的满意程度根据目标取值的上限和下限确定，最小化期望目标的满意度计算公式为：

式中，F为决策者对优化目标的满意度；x为优化目标值；xmax为目标优化上限；xmin为目标优化下限。

同理，最大化期望目标的满意度计算公式为：

2 基于故障率分布的舰艇维修备品备件多目标模糊配置模型

2.1 舰艇装备保障率计算模型

考虑到舰艇作战的特殊环境，舰艇装备维修通常实施换件维修，即当装备出现故障时，不用对零件做处理，直接用备品备件代替故障件，以保障装备的可靠性。装备保障率是指在战时，通过对舰艇装备所需的备品备件进行更换，使装备始终保持有效运行状态的概率[4]。由此可见，舰艇装备保障率的高低与其所携带的备品备件的寿命特点有关。通常情况下，备品备件可以分为指数分布寿命件、正态分布寿命件和威布尔分布寿命件。

2.1.1 指数分布寿命件平均失效概率计算

舰艇装备中的指数分布寿命件通常是指具有恒定故障率的电子元器件，在损耗前正常使用的复杂部件或由于随机高应力导致故障的部件，以及一些弱损耗部件也可以视为指数分布寿命件。

指数分布寿命件的失效概率密度函数f（t）可以表示为：

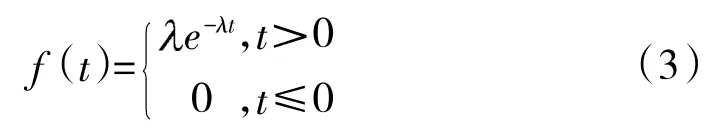
式中，t为指数分布寿命件工作时间；f（t）为指数分布寿命件失效概率密度；为分布参数，＞0。

指数分布寿命件的分布函数F（t）可以表示为：

根据分布函数可知，指数分布寿命件随着工作时间的增加，其失效概率递增。对含有该类备品备件的舰艇装备的维修保障过程中，通过增加指数分布寿命件的配置数量，在舰艇执行作战任务时间一定的条件下，可以有效缩短单个指数分布寿命件的工作时间，进而降低装备中该型备品备件的平均失效概率，提升装备可靠性。

指数分布寿命件的平均失效概率与配置数量的关系可以表示为；

式中，x为指数分布寿命件的配置数量；T为舰艇任务执行时间；P（x）为指数分布寿命件平均失效概率。

2.1.2 正态分布寿命件平均失效概率计算

正态分布寿命件主要包括在平均寿命期集中损坏的一类备品备件，如轮胎、变压器、灯泡、直升机旋翼叶片等。

正态分布寿命件的失效概率密度函数f（t）可以表示为：

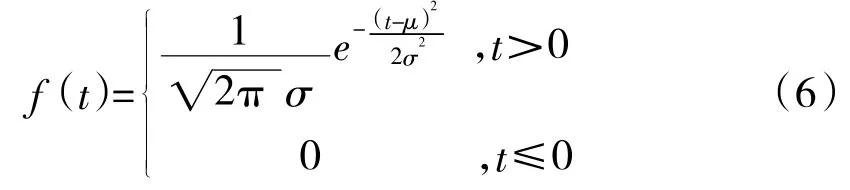
式中，t为正态分布寿命件工作时间；f（t）为正态分布寿命件失效概率密度；μ、σ为分布参数，σ＞0。

正态分布寿命件的分布函数F（t）可以表示为：

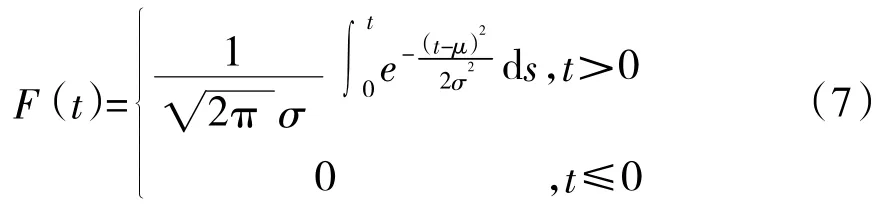
与指数分布寿命件类似，通过增加正态分布寿命件的配置数量，可以有效缩短单个正态分布寿命件的工作时间，进而降低装备中该型备品备件的平均失效概率，提升装备可靠性。

正态分布寿命件的平均失效概率与配置数量的关系可以表示为；

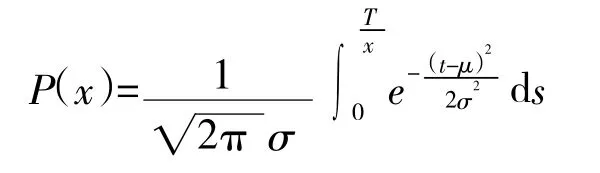
式中，x为正态分布寿命件的配置数量；T为舰艇任务执行时间；P（x）为正态分布寿命件平均失效概率。

2.1.3 威布尔分布寿命件平均失效概率计算

威布尔分布寿命件主要是指机电类产品的磨损累计失效形式，典型的威布尔分布备品备件包括滚动轴承、继电器、陀螺、电动机、发动机、蓄电池、液压泵、材料疲劳等[5]。

威布尔分布寿命件的失效概率密度函数f（t）可以表示为：

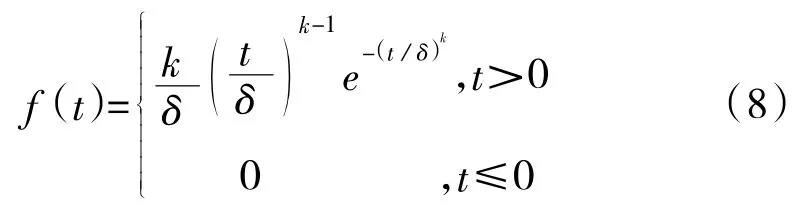
式中，t为威布尔分布寿命件工作时间；f（t）为威布尔分布寿命件失效概率密度；k、δ为分布参数，k，δ＞0。

威布尔分布寿命件的分布函数F（t）可以表示为：

与指数分布寿命件类似，通过增加威布尔分布寿命件的配置数量，可以有效缩短单个威布尔分布寿命件的工作时间，进而降低装备中该型备品备件的平均失效概率，提升装备可靠性。

威布尔分布寿命件的平均失效概率与配置数量的关系可以表示为；

式中，x为威布尔分布寿命件的配置数量；T为舰艇任务执行时间；P（x）为威布尔分布寿命件平均失效概率。

2.1.4 含有多种备品备件的舰艇装备保障率计算

通常情况下，一型舰艇装备由多种不同寿命分布类型的备品备件组成，当其中任何一个备品备件失效时，则该舰艇装备失效[6]。假设某一个舰艇装备由m个相同类型的指数分布寿命件，n个相同类型的正态分布寿命件和q个相同类型的威布尔分布寿命件组成，则该舰艇装备保障率与3种备品备件的配置数量x，y，z的关系可以表示为：

式中，x为指数分布寿命件的配置数量；y为正态分布寿命件的配置数量；z为威布尔分布寿命件的配置数量；T为舰艇任务执行时间；m为该舰艇装备所含有的指数分布寿命件个数；n为该舰艇装备所含有的正态分布寿命件个数；q为该舰艇装备所含有的威布尔分布寿命件个数；λ，σ，μ，δ，k 为备品备件的分布参数，λ，σ，μ，δ，k＞0。

通过公式可以看出，舰艇装备的保障率与保障该装备的备品备件配置数量有关，随着各型备品备件的配置数量增加，装备中各备品备件组成单元的平均失效概率降低，舰艇装备保障率随之提升。

2.2 舰艇维修备品备件保障费用计算

战场条件下，为了保障装备的可靠性，舰艇编队都会携带一定的备品备件，然而其数量并不是越多越好，备品备件携行过多不仅会造成损失和浪费，大大增加战时舰艇维修保障费用，而且还会占用大量的舰艇空间，限制舰艇综合保障能力的提升[7]。因此，有必要根据备品备件配置数量与保障费用之间的关系，对备品备件资源配置进行约束。

舰艇维修备品备件保障费用主要由两部分组成。一是为保障舰艇装备维修所需配置的备品备件的订购费用，不同类型的备件往往具有不同的订购单价，随着备件配置数量的增多，订购费用呈现线性增长；二是由于备品备件配置数量不足造成的舰艇装备停机而产生的损失费用，主要包括停机损失、维修或保障延迟所占用的费用等[8]。

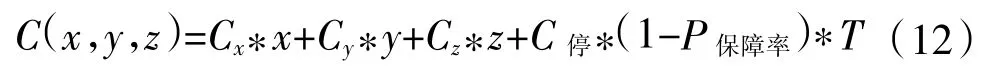
假设保障某一舰艇装备的3种类型备品备件的配置数量分别为x，y，z，则备品备件保障费用的计算公式为：式中，x为保障该装备的指数分布寿命件的配置数量；y为保障该装备的正态分布寿命件的配置数量；z为保障该装备的威布尔分布寿命件的配置数量；Cx为指数分布寿命件的单位订购费用；Cy为正态分布寿命件的单位订购费用；Cz为威布尔分布寿命件的单位订购费用；C停为舰艇装备停机损失费用；T为舰艇任务执行时间；P保障率为3种备件配置数量分别为x，y，z条件下的舰艇装备保障率。

2.3 舰艇维修备品备件多目标模糊配置决策

战场条件要求备品备件资源配置更多的面向舰艇装备保障率的提升，同时备品备件配置数量也要满足战时保障费用约束[9]。这两个因素通常是相互制约的：当要求更高装备的保障率就意味着投入更大的保障费用，而减少保障费用时会使装备的保障率无法达到要求[10]。一般情况下舰艇执行的作战任务不同，目标权重往往不同，高强度、短时间的作战任务要求更高的舰艇装备保障率；相反，低强度、长时间作战任务则对节约保障费用提出更高的要求。

根据舰艇执行作战任务的特点不同，分别对舰艇装备保障率和备品备件保障费用设立目标期望值，进而根据目标取值的上限和下限分别建立决策满意度函数，对满意度函数赋以权重，求得总满意度最高的备品备件资源配置方案。

假设保障某一舰艇装备的3种类型备品备件的配置数量分别为x，y，z，则战时舰艇装备保障率的满意度函数表达式为：

式中，U保为决策者对舰艇装备保障率的满意度；α为决策者对舰艇装备保障率的满意上限；β为决策者对舰艇装备保障率的满意下限；

假设保障某一舰艇装备的3种类型备品备件的配置数量分别为x，y，z，则战时备品备件保障费用的满意度函数表达式为：

式中，U费为决策者对备品备件保障费用的满意度；Cα为决策者对备品备件保障费用的满意上限；Cβ为决策者对备品备件保障费用的满意下限；

根据舰艇执行作战任务的特点不同，分别对舰艇装备保障率的满意度函数和备品备件保障费用的满意度函数赋予权重，进行加权求和，即为决策者总满意度函数。

计算总满意度最大时该舰艇装备对应的3种类型备品备件的配置数量x，y，z，即为战时备品备件资源的最优配置。运用本模型分别计算舰艇各装备各型备品备件的配置数量并累加，得到该艘舰艇战时的备品备件资源配置方案。

3 案例分析

执行某作战任务舰艇的某一型舰艇装备由4个可更换备品备件组成，其中包括2个相同类型的指数分布寿命件、1个正态分布寿命件和1个威布尔分布寿命件。根据同类型备品备件的历史统计数据分析，指数分布寿命件的故障率参数λ=1/80 000 h，正态分布寿命件的平均寿命参数μ=2 400 h、标准差σ=200 h，威布尔分布寿命件的尺度参数δ=12 000 h、形状参数k=2，3种备品备件的单价分别为Cx=20 000元、Cy=8 000元、Cz=40 000元，单位时间停机损失C停=1 000元/h，舰艇执行任务时间T=4 000 h。

根据上述分析，分别建立舰艇装备保障率函数和备品备件保障费用函数。

由于舰艇装备保障率P保障率的取值范围为0-1，以舰艇装备保障率函数直接作为决策者的满意度函数，即：

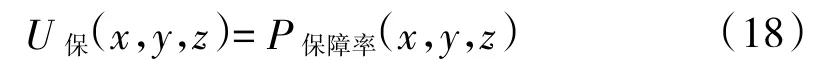
取备品备件保障费用满意上限Cα=200万元，满意下限Cβ=20万元，建立决策者对保障费用的满意度函数。

高强度、短时间任务要求提升舰艇装备保障率的满意度函数权重；相反的，低强度、长时间任务则要求备品备件保障费用的满意度函数具有较大的权重。根据舰艇作战任务特点，分别取ω保=0.9，ω费=0.1，得到舰艇维修备品备件资源配置的总满意度函数。

分别对x，y，z求偏导数，令偏导数等于零，求解总满意度函数最大值。

解方程可得，x=14.24，y=2.99，z=5.03，因此，保障该舰艇装备的备品备件资源配置方案为：指数分布寿命件的配置数量为14个、正态分布寿命件的配置数量为3个、威布尔分布寿命件的配置数量为5个。根据模型的意义，当前配置方案满足了战时的维修保障费用约束，同时提升了装备保障率，有效保障了该舰艇装备作战任务能力的发挥。

当前配置方案下的该舰艇装备保障率和备品备件保障费用如表1所示。