时变平坦衰落SIMO信道中的信噪比盲估计*

李 涛，许 华，蒋 磊

（空军工程大学信息与导航学院，西安 710077）

0 引言

通信信号的信噪比（SNR：Single-to-Noise-Ratio）是反应通信信号质量的一个重要指标，而且在无线通信中的许多场合，如分集接收中的最大比合并、调制信号识别、Turbo编码中的迭代译码、移动通信中的功率控制、码分多址中各链路的功率分配等，都需要将信噪比作为先验信息[1]，信噪比估计的准确度直接影响到通信系统的性能，因而信噪比估计算法的研究是一项重要课题。

目前，对于非衰落信道下的信噪比估计算法[2-7]研究最充分，主要有基于似然函数、统计量和子空间分解的方法，特别是在有数据辅助下，最大似然估计（ML）性能基本达到理论下限，而且实现简单。而对于高速移动终端，恒定信道的经典假设不符合实际，如果想要跟踪快速变化的信道参数，需要插入大量的导频序列，会降低信息传输速率。而且，对于频谱检测、通信侦查和其他非合作接收中，导频序列极难获得。在现实中，信道往往是衰落信道，因此，对时变衰落信道下的信噪比盲估计算法[8]的研究是一项重要的课题。

本文基于EM算法的迭代期望值最大化思想，首先推导了时变平坦衰落SIMO信道下EM算法的闭式解，实现了对信噪比的盲估计。为进一步改善性能，利用M2M4算法得到待估参数的粗略值，对EM算法进行初始化，从而加快EM迭代算法的收敛速度并提高其估计精度。

1 信号模型

考虑恒包络调制信号（下文以MPSK调制信号为例），在信号经过时变平坦衰落SIMO信道后，接收端经过时间同步和匹配滤波后，第i（i=1，2，…，Nr）个天线单元接收信号模型可以表示为：

其中，Ts为采样间隔，与符号间隔相等，N为处理窗口长度，nTs表示离散时间的瞬时时刻（下文用tn表示）。x（tn）表示tn时刻的发送信号，hi（tn）表示第i个天线单元的瞬时信道复增益，ωi（tn）表示复高斯白噪声，均值为0，方差为2σ2。将hi（tn）进行L-1阶泰勒级数展开，如下：

当L太大时，可能导致数值不稳定，本文根据FD通过选取合适的N和Fs，使为无穷小。

2 EM算法

整个EM算法的迭代过程由两部分组成：

E步：根据前一次得到的θ估计值计算似然函数 L（θ|xk）的数学期望值；

M步：求新的θ估计值使E步骤中的数学期望值最大化。

定义如下向量：

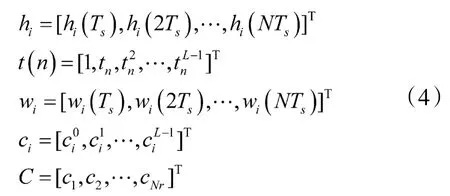
发送端发送 x（n）（即 x（tn）），接收端所有天线单元的接收矩阵y（n）可以表示为：

由式（5）得y（n）的先验概率密度函数为：

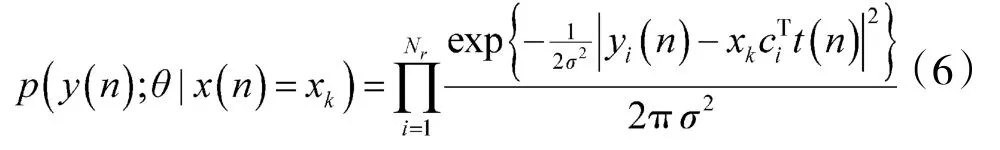
其中，xk可以是MPSK的任意一个星座点，θ表示待估向量ci和参数σ2。对于发送符号x（n），待估参数θ的似然函数为：

定义关于θ的函数Q：

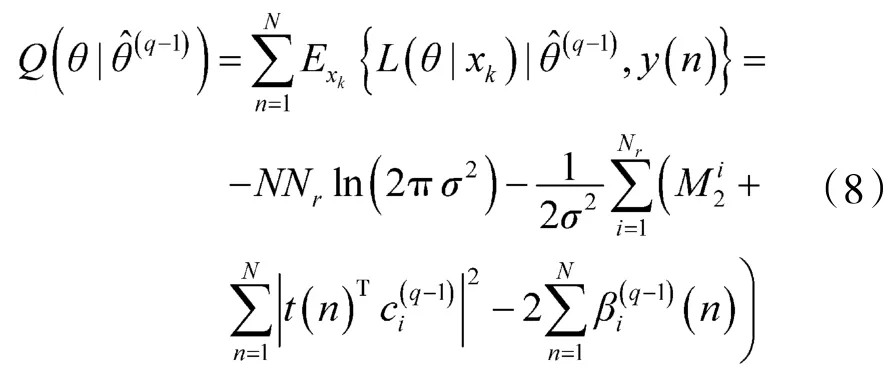
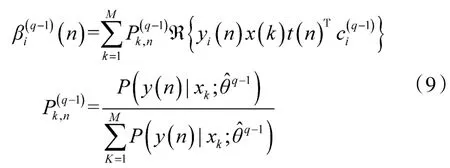
由于ci由实部和虚部构成，即：

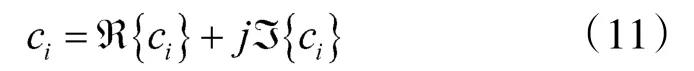
其中，

将式（8）对 σ2求导并置 0，求得 σ2（q）的最大似然估计值为：

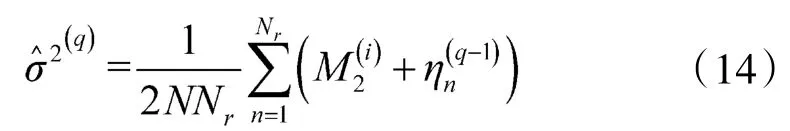
其中，

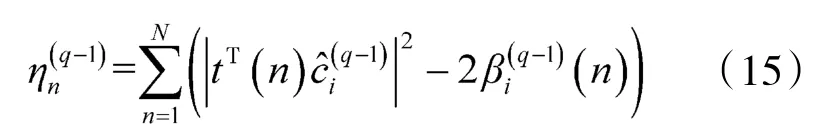
利用ci和σ2的估计值，第i个天线单元的信噪比最大似然估计值可以表示为：

3 基于M2M4的参数初始化

EM算法具有收敛性[9]，但一般情况下，EM算法的结果只能保证收敛到后验分布密度函数稳定的点，并不能保证一定收敛到所求问题的极大似然解。如果似然函数具有多极值，则EM算法只能保证收敛于某一局部极大值处，在这种情况下，EM算法能否收敛到全局极大值处，取决于算法初值的选取。

M2M4估计方法[10]利用接收信号的二阶和四阶矩的相互关系来进行参数估计，是一种自适应全盲算法，不需要载波相位的恢复，不需要接收机进行判决，而且运算量相对较小。采用较小运算量的M2M4算法对θ进行初始化，能快速提高EM算法的收敛速度，减少迭代次数，并尽可能使算法收敛到全局最大值处。

为简化初始化信号模型，当NFD较小时，第i个天线单元的时变信道增益可以当作常数，假设高斯白噪声 ωi功率为 Pi，即 Pi=2σ2。则式（1）的接收信号模型重写为：

第i个天线单元接收信号的2阶和4阶统计量分别为：

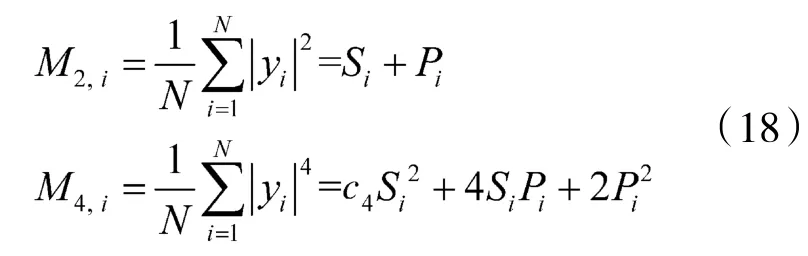
参数 ci，σ2初始化为：

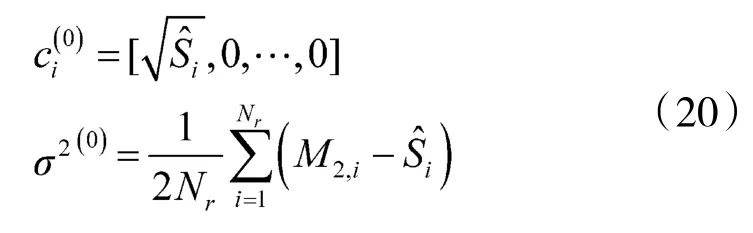
4 仿真与结果分析

为检验M2M4-EM算法性能，本文以常见的QPSK和16-QAM恒包络信号为例，分别仿真了EM算法和M2M4-EM算法在不同信噪比和接收天线单元数量下的性能，以信噪比的归一化均方误差（NMSE）作为性能指标，即：

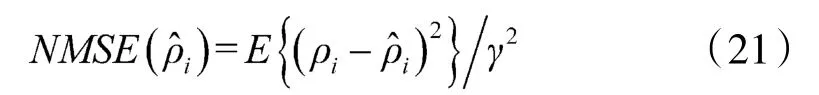
图1是QPSK信号在不同γ下，两种SNR估计算法独立进行5 000次MonteCarlo试验的NMSE对比。仿真条件设置为：N=56，Nr=3，L=4，Fs=14 000 Hz且FD/Fs=7.14×10-3。仿真时，EM迭代10次，初值；M2M4-EM算法仿真中仅进行4次迭代，初值由M2M4算法求得，其余仿真条件相同。

图1 不同γ下QPSK信号的SNR估计算法的NMSE对比

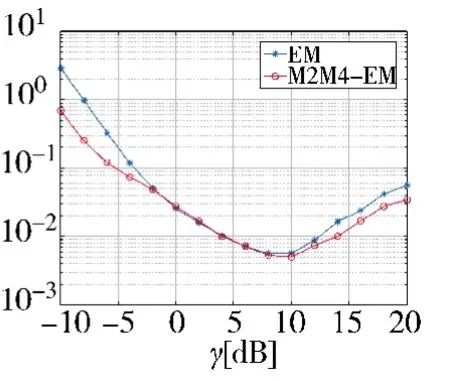
图2 不同γ下16-QAM信号的SNR估计算法的NMSE对比

从图1中两算法的性能曲线中可以看出，算法在较宽的信噪比范围内都具有较好的性能。M2M4-EM算法在迭代4次的情况下性能优于迭代10次的EM算法，且这种优势在信噪比低于-2 dB时更加明显。信噪比在-2 dB～8 dB时，两种算法性能几乎无异。当信噪比高于8 dB时，由于初始值不够精确，两种算法的性能相对降低。

表1为在上述5 000次MonteCarlo仿真中，两种算法的时间开销数据对比。可以看出，与EM算法相比，M2M4-EM算法耗时少近60%。

表1 两种算法的时间开销对比

图2是针对16-QAM信号进行的仿真，其他仿真条件与图1相同。从图中可以看出，两条性能曲线与图1相似，表明算法对恒包络信号都具有较好的实用性。

图3是在不同接收天线单元数量下，两种SNR估计算法的性能曲线，其他仿真条件与图1相同，EM算法迭代10次，M2M4-EM算法仅迭代4次。从图中可以看出，随着接收天线数量的增加，算法性能越好，且M2M4-EM算法性能始终优于EM算法；当接收天线数量大于6时，M2M4参数初始化算法的估计精度得到提升，使M2M4-EM算法性能得到显著提高。

图3 不同接收天线单元数量对两种SNR估计算法性能影响

5 结论

针对恒包络信号在时变平坦衰落SIMO信道下的信噪比盲估计问题，提出一种基于EM算法的改进M2M4-EM算法。首先利用了常规EM算法的迭代期望值最大化思想，推导出了SIMO信道下EM算法的闭式解。为了进一步提高算法性能，通过M2M4算法利用接收信号的二阶四阶矩得到待估参数的粗略值，对EM算法进行初始化，从而加快EM迭代算法的收敛速度并提高其估计精度。通过仿真算法在不同信噪比和接收天线单元数量下的性能，说明了M2M4-EM算法在较宽的信噪比范围内具有较好的估计精度和较快的收敛速度，在接收天线数量大于6时，能减小EM算法在高信噪比时由于初值偏差过大引起的估计误差，具有良好的实际应用价值。