一类具有限制联盟结构的合作对策的两阶段Shapley值

王利明

(1.内蒙古财经大学 统计与数学学院,内蒙古 呼和浩特 010070; 2.内蒙古经济数据分析与挖掘重点实验室,内蒙古 呼和浩特 010070)

0 引言

在合作对策中，联盟结构是指局中人集合的一个划分,划分中的每个子集表示局中人结成的一个优先联盟。 优先联盟内的局中人或者同时参与合作，或者同时不参与合作，即以整体的姿态参与大联盟的合作。 很多学者对具有联盟结构的合作对策进行研究，给出了解的概念，如Owen值[1]，Banzhaf-Owen值[2],对称联盟Banzhaf值[3]等。 2009年，Kamijo[4]从不同角度定义了具有联盟结构的合作对策的一个解，因在优先联盟之间和优先联盟内部分别计算Shapley值，称之为两阶段Shapley值(two-step Shapley value)。

在经典的具有联盟结构的合作对策中，通常假设优先联盟作为一个整体互相之间可以任意结盟，优先联盟内部的局中人也可以任意结盟。 然而在现实生活的合作实践中，经常会出现优先联盟之间或内部结盟有限制的情形。 基于此，学者们讨论了具有限制联盟结构的合作对策。 例如，Kongo[5]，van den Brink等[6]，Béal等[7]研究了优先联盟之间和内部具有交流结构限制的合作对策，Meng等[8,9]研究了凸几何上的具有联盟结构的合作对策、扩张系统上的具有联盟结构的合作对策，孙红霞等[10]研究了优先联盟之间具有格结构的合作对策。

在文献中被广泛研究的另外一类具有合作限制的合作对策是具有权限结构的合作对策[11,12]。 在这类合作对策中，局中人需要其上级的许可才可以参与合作并发挥作用。 本文讨论局中人结成优先联盟参与合作且优先联盟内有权限结构限制的合作对策。 利用两阶段Shapley值的分配思想给出这类合作对策的一个解，证明其满足的公理体系，并通过例子验证了公理的独立性。

1 预备知识

1.1 合作对策

用N={1,2,…,n}记局中人集合，v:2N→R满足v(Ø)=0，则称(N,v)为一个合作对策。∀E⊆N，v(E)表示联盟E内局中人通过合作获得的收益。 在不致引起混淆的情况下，合作对策(N,v)也用其特征函数v来表示。N上的所有合作对策记为GN。

设N′⊆N，称(N′,v|N′)是(N,v)的一个子对策，其中v|N′是v限制在N′上得到的函数，即v|N′(E)=v(E)，∀E⊆N′。 如果v∈GN满足v(E)≤v(F)，∀E⊆F⊆N，称v是单调的。 如果i∈N满足v(E∪{i})=v(E)，∀E⊆N{i}，则称i是v中的零元。 如果i∈N满足v(E∪{i})=v(E)+v({i})，∀E⊆N{i}，则称i是v中的哑元。如果i∈N满足v(E)=0，∀E⊆N{i}，则称i是v中的必要元。 如果i,j∈N满足v(E∪{i})=v(E∪{j})，∀E⊆N{i,j},则称i和j在v中对称。

映射ξ:GN→Rn称为合作对策的一个单值解(简称解)，其中ξi(v)表示分给局中人i∈N的收益分配值。Shapley值[13]是被广泛应用的一个单值解，定义如下:

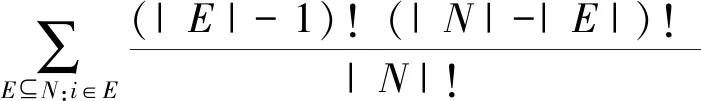
(v(E)-v(E){i}),∀i∈N

1.2 具有联盟结构的合作对策

映射ξ:GN×CN→Rn称为具有联盟结构的合作对策的一个解。 Kamijo[4]定义的具有联盟结构的合作对策的两阶段Shapley值如下：

1.3 具有权限结构的合作对策

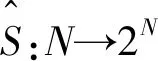
van den Brink等[12]对合取Shapley权限值进行了公理刻画。 下面给出解ξ:GN×SN→Rn需要满足的一些性质。

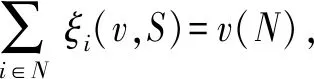
可加性 对任意v1，v2∈GN，S∈SN,有ξ(v1+v2,S)=ξ(v1,S)+ξ(v2,S)。

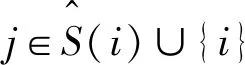
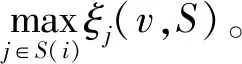
必要元性 设v∈GN是单调的，S∈SN，i是合作对策v中的必要元，则ξi(v,S)≥ξj(v,S)，∀j∈N。

定理1[12]合取Shapley权限值φ是满足有效性，可加性，非本质元性，必要元性和结构单调性的唯一解。

2 联盟内部限制两阶段Shapley值

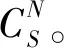
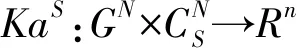
注如果Sk(Ck)=Ø,∀k∈M，则限制TS值KaS就是两阶段Shapley值[4];如果Γ={N}，则KaS就是合取Shapley权限值[11];如果Γ={{1},{2},…,{n}}，则KaS就是Shapley值[12]。

限制TS值KaS可以看作通过下面的两阶段分配得到的。

第一步，将大联盟的收益根据商对策u的Shapley值分配给各个优先联盟，即每个优先联盟Ct获得的分配为Sht(u)。

第二步，将每个优先联盟Ct在第一步获得的收益Sht(u)分配给内部各个局中人：v(Ct)部分根据具有权限结构的对策(v|Ct,St)的合取Shapley权限值分配给Ct内各局中人，优先联盟在第一步获得的合作增益Sht(u)-v(Ct)以平均分配的方式分给Ct内各局中人。

例设N={1,2,3,4,5}，N上的合作对策定义为:v({i})=0,∀i∈N;

v({1,2})=3,v({3,4})=3,v({3,5})=4,v({4,5})=3，其余v({i,j})=0;

v(S)=2|S|，∀S⊆N且|S|=3或4;

v({1,2,3,4,5})=15。

N上的限制联盟结构ΓS为:Γ={C1,C2}，其中C1={1,2},C2={3,4,5};S1(1)={2},S1(2)=Ø;S2(3) ={4,5},S2(4)=Ø,S2(5)=Ø。

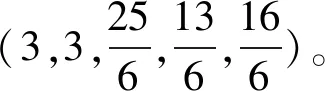
下面给出限制TS值的公理刻画结论，并通过一些解的例子说明这些公理是相互独立的。

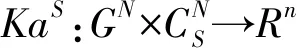
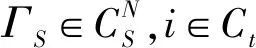
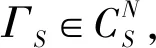
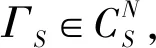
证明首先证明KaS满足上述六条公理。

(1)有效性。由KaS的定义及Shapley值、合取Shapley权限值均满足有效性，有

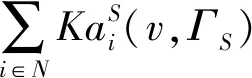
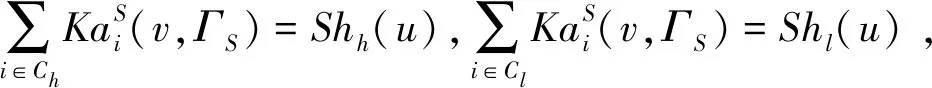
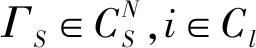
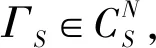
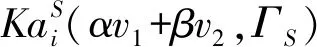
φi((αv1+βv2)|Ct,St)

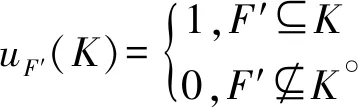
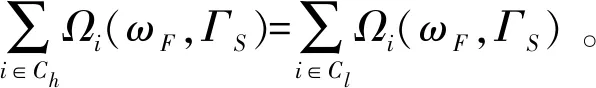
若k∉F′，则k是商对策uF′中的哑元，且∀i∈Ck，i是ωF中的零元，从而是(N,ωF,ΓS)中的非本质元。 由联盟非本质元性，对任意i∈Ck且k∈MF′,Ωi(ωF,ΓS) =0。

再由有效性得到

(1)

分两种情形讨论优先联盟Ck内部的分配。

情形1f′=1。

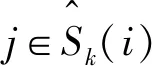
由于每个i∈F都是ωF|Ck中的必要元，因此存在某个常数c，Ωi(ωF,ΓS)=c,∀i∈F且Ωi(ωF,ΓS)≤c,∀i∈αk(F)F。再由联盟内部结构单调性得到Ωi(ωF,ΓS)≥c,∀i∈αk(F)F。结合式(1)，得到

情形2f′≥2。

若k∈F′，则对任意E⊆Ck，ωF(E)=0。因此任意i∈Ck，均是子对策ωF|Ck的必要元。 由联盟必要元性，Ωi(ωF,ΓS)=Ωj(ωF,ΓS),∀i,j∈Ck。

下面通过给出几个解的例子说明定理中公理化条件的独立性。

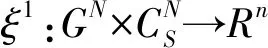
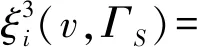
φi(v|Ct,St),∀i∈Ct∈Γ

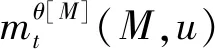
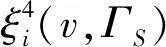
则ξ4满足有效性，联盟非本质元性，联盟对称性，联盟必要元性，可加性，但不满足联盟内部结构单调性。

联盟必要元性:定义f5:GN×SN→Rn为:

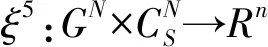
容易验证，ξ5满足有效性，联盟非本质元性，联盟对称性，联盟内部结构单调性，可加性，但不满足联盟必要元性。

可加性:定义f6:GN×SN→Rn为:

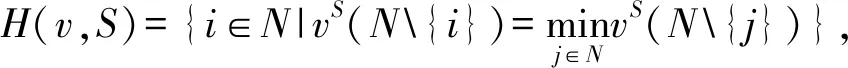
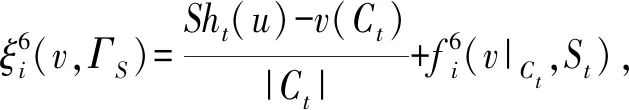
ξ6满足有效性，联盟非本质元性，联盟对称性，联盟内部结构单调性，联盟必要元性，但不满足可加性。

3 结束语

本文讨论了局中人通过优先联盟整体参与合作，并且优先联盟内部有合取权限结构限制的合作对策，在优先联盟内有些局中人需要获得其他局中人的许可才能参与合作。 利用两阶段Shapley值和合取Shapley权限值定义了这类合作对策的解，并用一组公理唯一地刻画该解，为现实社会中相应情形下的合作收益分配问题提供了一种定量方法和理论支持。 在后续的研究工作中，可进一步考虑其它的联盟结构限制方式，如二级权限结构，即优先联盟之间和内部均具有权限结构限制的合作对策。 或者利用具有联盟结构的合作对策的其它解，如Banzhaf-Owen值，对称联盟Banzhaf值等，从不同角度给出更多的分配方式。