基于演化博弈的工程项目施工安全管理分析

廖 佳， 周 强

(成都理工大学工程技术学院 资源勘查与土木工程系，四川 乐山 614000)

0 引言

建筑业已成为我国第二大高危行业，建筑生产过程中的安全问题亟待解决。安全事故的产生除因施工人员操作不规范之外，更重要的原因在于有限理性的施工管理方出于眼前利益的考虑，在安全风险和经济利益之间博弈，违规施工并向监理支付相应费用，使其放弃督促整改所致。继2016年江西丰城电厂“11.24”特重大事故，今年广州在建电厂发生的“3.25”安全事故再次警示了施工现场安全管理和有效监督整改的重要性，如何建立科学的约束机制来制衡双方严格按规范施工和监督，保障施工现场的安全稳定就成为项目管理者研究的重点。

对于工程项目的安全管理，国外主要从安全制度的完善、安全环境、安全文化及教育、工人安全行为、项目经理的选择、安全风险预防等角度进行实证和理论研究[1～6]，演化博弈在工程中主要用于结构、公路交通、桥梁设计约束优化、工程承包商腐败等方面[7～10]。国内运用演化博弈分析安全管理的文献较多，具体如下：程敏，陈辉[11]运用演化博弈对政府安监部门与施工单位在安全生产中的演化稳定状态进行了分析，并提出相应安全监管措施；WANG[12]，ZENG[13]，谭翀等[14]也作了类似的研究。冯群，石学军等[15]以国家、政府安监部门、建筑企业为研究对象，建立两两之间的演化博弈模型，探讨各自的策略选择及演化稳定均衡。贾璐[16,17]运用演化博弈从不同角度对政府、施工单位和监理单位的演化策略进行研究，并借助系统动力学进行仿真，以此提出相应措施和建议。俞乐，周洪涛等[18]构建政府和监理单位的演化博弈模型，探讨二者的演化稳定策略及均衡并进行仿真。周国华，张羽等[19]建立施工管理方和施工人员的演化博弈模型，引入前景理论分析双方演化均衡及影响因素，对其进行实证研究和仿真分析。王旭峰，刘毅等[20]基于组织的复杂网络，构建工人参与安全管理的演化博弈模型，分析工人参与安全管理意愿的主要影响因素，并对不同初始值下的演化进行数值模拟。杨世军，张羽等[21]以施工管理方和施工人员为研究对象，建立双方演化博弈模型，分析双方演化均衡及影响因素，并据以提出相应建议；SUN等[22]也作了类似的研究。

从现有文献可看出，演化博弈在安全管理的研究主要集中在从宏观上分析国家、政府安监部门、监理单位、施工单位之间的双方或三方之间的博弈，或是探讨施工现场管理方与建筑工人之间的博弈。但是，在我国现行项目经理责任制和总监负责制的形势下，建筑工人归属于施工现场管理方的管理，而政府和公司只在一定程度上起到监管作用，施工现场管理方和监理方的行为和策略选择才是影响项目成败的关键因素，而现有文献未见运用演化博弈和相位图对二者之间的博弈进行系统分析。鉴于此，本文基于施工现场管理方和监理方有限理性，运用演化博弈理论，从动态的角度探讨双方在施工过程中博弈的演化稳定策略，分析参数变化对演化稳定策略的影响，通过MATLAB R2014a进行验证，提出相应建议，为建立规范的安全生产管理秩序提供一定的理论依据。

1 安全施工管理模型构建与分析

1.1 模型假设与复制动态方程的建立

作为工程项目的现场管理者，施工方的施工管理和监理方的监督管理在项目实施过程中发挥了无可替代的作用，二者基于自身利益的策略选择是影响项目安全的根本原因。由于双方作为经济人并不具备完全理性，在施工过程中会在“自身利益”和“工程安全风险”之间进行博弈，而做出不同策略选择，从而影响工程安全。为探究工程项目安全管理，本文运用演化博弈对双方在施工过程中的演化策略进行分析。其模型假设如下：

(1)假设工程项目内施工方和监理方知识结构是共同知识，以保证双方在现场施工过程中具有相应的决策信息，使其自身利益达到最大化[23]。记施工方策略空间为按规范安全施工和违规施工；监理方的策略为严格监理和不监理。

(2)项目内的主体i=(1，2)都是有限理性主体，施工方(i=1)和监理方(i=2)之间存在非对称博弈。

(3)∏i(i=1，2)为双方项目完成项目的正常收益。

(4)S为施工方违规施工，将安全施工费转移节约的费用；K为施工方向监理方支付的默认其违规的成本；γ为安全事故发生的概率，γ∈[0,1]。

(5)D为施工方违规施工被监理方要求整改增加的费用(D>S)。

(6)Ci(i=1，2)为安全事故发生后对施工方和监理方的罚款。

(7)Wi(i=1，2)为施工方违规施工和监理方未按规范规定严格监理造成的声誉损失。

具体的支付矩阵如表1所示：

表1 施工方和监理方博弈支付矩阵

假定施工方选择安全施工策略概率为p，违规施工策略概率为1-p；监理方选择严格监理策略的概率为q，不监理策略的概率为1-q。则对施工方有：

采取安全施工的适应度：

UA(S1)=Π1q+Π1(1-q)=Π1

(1)

采取违规施工的适应度为：

UA(S2)=(Π1+S-D-W1)q+

[Π1+S-K-γ(C1+W1)](1-q)

=[K+γ(C1+W1)-D-W1]q+

[Π1+S-K-γ(C1+W1)]

(2)

平均适应度为：

UA(S)=pUA(S1)+(1-p)UA(S2)

=Π1+[K+γ(C1+W1)-D-W1]q(1-p)+

[S-K-γ(C1+W1)](1-p)

(3)

根据演化博弈原理，由式(1)和(3)可得施工方采取安全施工策略的复制动态方程为：

q-[S-K-γ(C1+W1)]}

(4)

同理，监理方采取严格监理策略的复制动态方程为：

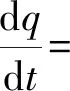
p-[K-γ(C2+W2)]}

(5)

1.2 施工方与监理方的演化稳定分析

当(4)(5)等于0时，可以得到五个平衡点：E1(0，0)，E2(0，1)，E3(1，0)，E4(1，1)，E5(p*,q*),其中

当p*,q*∈[0,1]时E5点存在。

按照文献[24]提出的方法，由Jacobi矩阵的局部稳定性分析可得系统的演化稳定策略(ESS)[24]。式(4)和式(5)构成的方程组，其雅可比矩阵为:

则有： detJ=(1-2p)(1-2q){[D+W1-K-γ(C1+W1)]q-[S-K-γ(C1+W1)]}

{[W2+K-γ(C2+W2)]p-[K-γ(C2+W2)]}-p(1-p)q(1-q)

[D+W1-K-γ(C1+W1)][W2+K-γ(C2+W2)]

(6)

trJ=(1-2p){[D+W1-K-γ(C1+W1)]q-[S-K-γ(C1+W1)]}+

(1-2q){[W2+K-γ(C2+W2)]p-[K-γ(C2+W2)]}

(7)

将E1(0，0)，E2(0，1)，E3(1，0)，E4(1，1)，E5(p*,q*)五个均衡点代入式(6)和式(7)，可知式(6)和式(7)的值由S-K-γ(C1+W1)和K-γ(C2+W2)所确定。显然，S-K-γ(C1+W1)表示施工方违规施工时，违规节约成本与付出期望成本的差值；K-γ(C2+W2)表示监理方对施工方违规施工行为不作为时获得收益与期望惩罚的差值。

故演化博弈可从S-K-γ(C1+W1)>0、S-K-γ(C1+W1)<0和K-γ(C2+W2)>0、K-γ(C2+W2)<0四种情况下讨论，稳定性分析结果见表2。

表2 稳定性分析结果

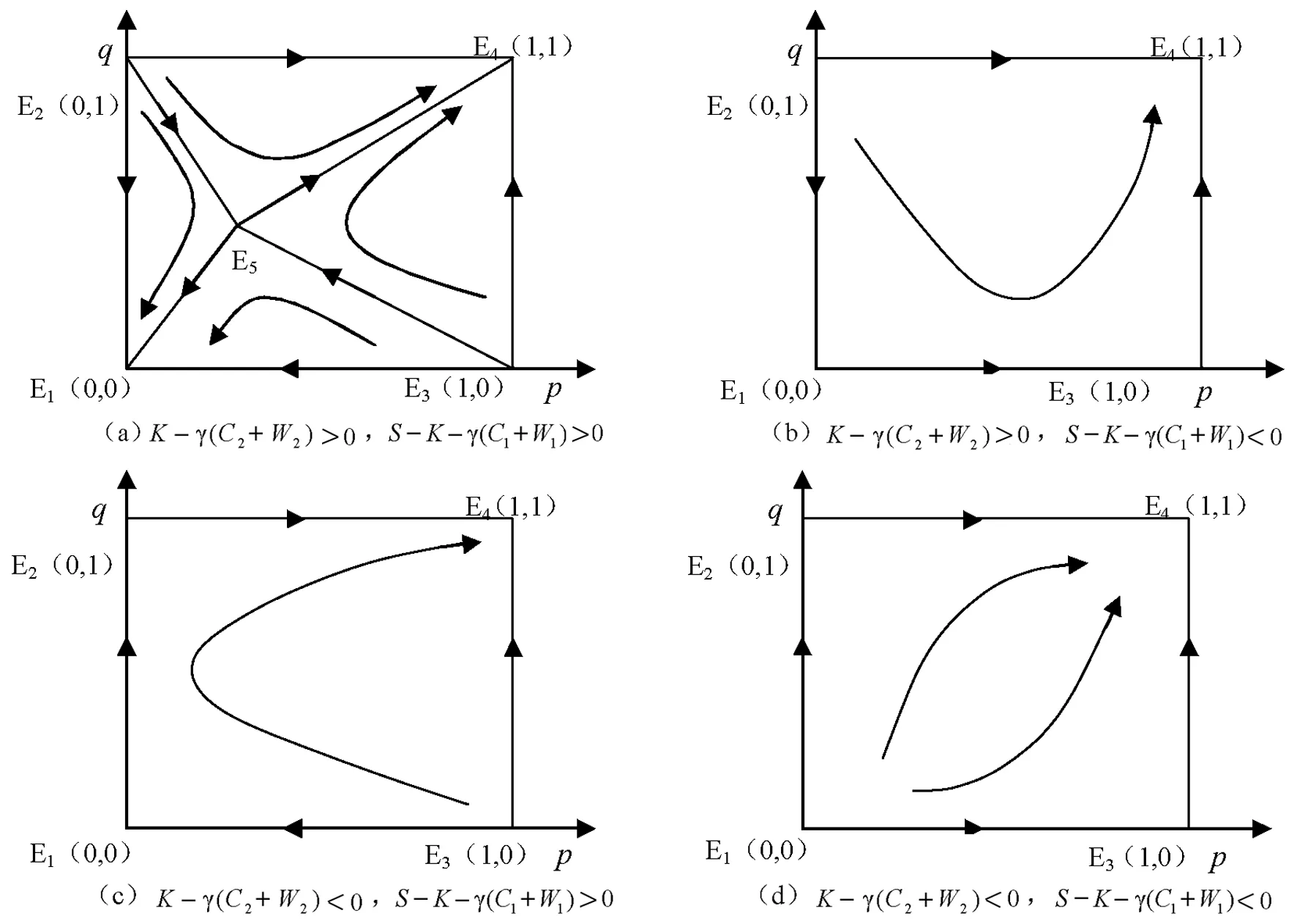
图1 演化博弈轨迹相位图

通过上述分析可知，双方的演化均衡结果为(安全施工，严格监理)或(违规施工，不监理)，以p、q为坐标轴表示的双方策略的动态演化博弈轨迹相位图如图1。

由相位图分析可知：

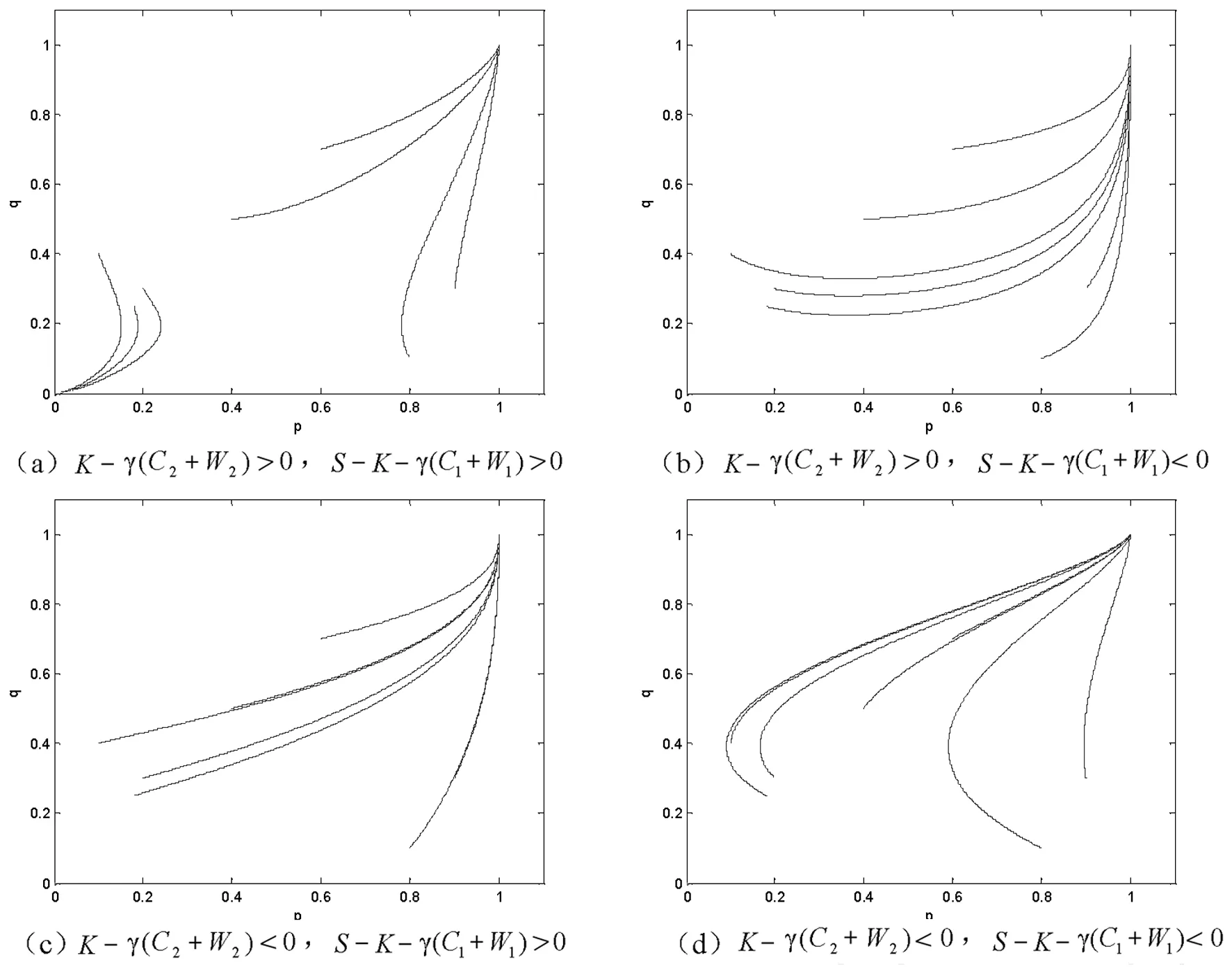
(1) 当K-γ(C2+W2)>0，S-K-γ(C1+W1)>0时，0

(2)当K-γ(C2+W2)>0，S-K-γ(C1+W1)<0时，由于01。对于施工方而言，违规所得收益小于支付给监理的允许其违规的成本和期望惩罚之和；对于监理方而言，不监理所得收益大于所受到的期望惩罚，如图1(b)所示，此时E1(0，0)、E3(1，0)为鞍点，E2(0，1)为不稳定点，即无论施工方和监理方的初始策略位于何处，最终都将收敛于(安全施工，严格监理)。

(3)当K-γ(C2+W2)<0时，对于监理方而言，通过不监理、允许施工方违规所得收益小于所受到的期望惩罚，因此，无论S-K-γ(D1+W1)的取值如何，严格监理是其占优策略，最终都将收敛于(安全施工，严格监理)，演化路径如图1(c)与图1(d)所示。

2 结果讨论

从上述分析可知，违规和不监理所得的净收益是影响二者演化均衡的重要原因，演化均衡的结果与博弈发生时的初始策略和鞍点E5(p*，q*)位置密切相关，影响策略选择的因素主要由鞍点E5(p*，q*)的位置决定，其中：

建筑市场安全管理、规范发展的演化均衡由E2E5E3E4的围成面积S所决定，由相位图1(a)可知：

具体参数分析为：

(1) 事故发生对双方的惩罚成本Ci。若发生安全事故，必然会受到相应惩罚从而减少自身收益，在其它变量不变的情况下，Ci越大，面积越大，系统收敛于E4的趋势越大，双方演化均衡结果为(安全施工，严格监理)。

(2)双方违约造成声誉损失Wi。Wi越大，面积越大，系统收敛于E4的概率越大，系统最终将朝(安全施工，严格监理)演化。

(3)施工方违规节约成本S。若S越大，面积越小，系统收敛于E4的概率越小，最终演化均衡结果为(违规施工，不监理)。

(4)事故发生概率γ，γ越大，面积越大，系统收敛于E4的概率越大，系统将朝着(安全施工，严格监理)演化。

(5)施工方违规被监理方要求整改费用D。D越大，面积越大，系统收敛于E4的概率越大，系统最终将朝着(安全施工，严格监理)演化。

(6)施工方支付给监理企业成本K。若K增大，面积可能增加也可能减少，系统的收敛将取决于K的大小，如果K大于监理方不监理时的期望惩罚成本，演化均衡为(违规施工，不监理)；反之，演化均衡结果为(安全施工，严格监理)。

3 数值模拟

为验证上述结果，运用MATLAB R2014a对二者的策略选择的演化轨迹进行数值模拟。其中图1对应四种情况参数设置见表3：

表3 四种情况参数设置一览表

易验证上述参数值满足四种情况的前提条件，并计算此时E5值(0.36，0.193)。选取{(p，q)|0≤p,q≤1}之间的如下七组数据：(0.1，0.4)、(0.18，0.25)、(0.2，0.3)、(0.4，0.5)、(0.6，0.7)、(0.8，0.1)、(0.9，0.3)，其中前三组属于E2E5E3E1、后四组属于E2E5E3E4进行模拟，所得复制动态演化轨迹见图2。

图2 图1对应的动态演化模拟图

(p为施工方选择安全施工策略概率，q为监理方选择严格监理策略概率)

从图2可知，图2(a)为图1(a)的数值模拟，此时系统演化分别收敛于(0，0)、(1，1)，系统最终收敛结果取决于初始状态的位置：当初始值位于E2E5E3E4区域时，最终将收敛于(安全施工，严格监理)，而当初始值位于E2E5E3E1区域时，最终将收敛于(违规施工，不监理)。图2(b)(c)(d)分别对应与图1(b)(c)(d)，即无论双方初始值如何选择，最终都收敛于(安全施工，严格监理)，且初始值越大，收敛速度越快。

4 结论及建议

通过对施工方和监理方演化博弈模型的研究可知，施工现场的安全稳定与事故发生的经济惩罚力度、声誉损失、事故发生概率、监理督促整改费以及施工方违规节约成本和支付给监理的费用等因素相关，具体取决于双方初始策略、违规和不监理所得的净收益。当经济和声誉惩罚力度大、支付给监理的费用高、违规和不监理的机会成本大于履约所耗成本，双方都选择严格履约，事故发生概率降低，系统将收敛于(安全施工，严格监理)；反之，则收敛于(违规施工，不监理)。

但在实际项目实施过程中，一方面由于施工方劳务水平参差不齐，工程安全管理和质量难以达到规范硬性要求；另一方面，在理性和利益博弈下，对于施工过程中某些安全隐患、质量偏差问题施工方和监理方已约定俗成：在小的问题上施工方违规支付费用而监理也会选择不作为，而在重大问题上施工方严格履约、监理方严格监理，因而在我国大多数项目实施过程中出现(安全施工，严格监理)，(违规施工，不监理)两种状态并存的状况；而当利益越过理性，问题大小把握失衡，又缺乏第三方监管，则易出现安全事故频发现象。

基于上述结论，若要实现施工现场的安全管理，主要可从合同约束、惩罚机制、加强监管、自律、劳务选择等方面着手制约各方利益，具体建议如下：

(1)在招投标时，优化招标文件，制定严格的施工企业、监理企业、项目经理、总监评选制度，明确企业和负责人所具备的资格和条件，选择合适的企业和经验丰富的项目经理、总监完成工程，制定措施防止企业中标后更换项目经理或总监牟取私利。

(2)在制定施工合同和监理合同时，根据二者的博弈利益，制定合理的经济惩罚和声誉约束机制，制衡双方的策略行为，建立基于业主平台的施工过程考评机制，在施工过程中让双方人员互评，并设置匿名举报和奖励制度，约束双方在施工中的行为，在一定程度上保障自身和工程的利益。

(3)政府管理机构严格建造师、监理工程师准入和执业制度，结合业主的施工考评结果建立项目负责人、总监及所在公司的征信记录体系，并将征信记录引入到评标系统，以适当的比例作为评标参考，影响其下次投标结果，增加二者的声誉损失成本，从而促使其按合同履约。

(4)加强对施工现场的监管，除设置监理之外，聘请第三方专业技术人员对施工安全状况进行随机抽查，并引入先进的管理技术，如BIM技术、物联网技术，实现工程的全过程管理与监督，促使双方自律履约。

(5)建立健全的施工劳务管理制度，对施工劳务人员严格考核获得资格后再进入岗位，并建立与其资格匹配的分级薪资制度，引导和鼓励专业工种劳务班组向品牌化技术企业转换。

除此以外，政府相关部门应加强安全生产监管力度，对违规施工和监理的责任人和企业进行严厉查处，淘汰信誉度低的人员和企业，以保障施工现场的安全稳定。