考虑保质期的非即时易腐品最优订购与定价决策
2019-06-11张锐,林峰,贾涛,2
张 锐, 林 峰, 贾 涛,2
(1.西安交通大学 管理学院,陕西 西安 710049; 2.过程控制与效率工程教育部重点实验室(西安交通大学),陕西 西安 710049)
0 引言
许多产品,例如蔬菜、水果、药品等,在零售阶段会由于损坏、变质、碰撞、蒸发等发生腐败,从而导致产品数量减少。根据Bakker等[1]的研究,易腐品基于贮藏特性可分为三种类别,包括(i)固定生命周期,(ii)随机生命周期,(iii)产品腐败率与其库存量减少速率相关。由于产品易腐特性对于零售商订购策略有着直接的影响,因而易腐品已成为库存理论研究的一个重要分支。基于需求率依赖于库存量,Hou[2]考虑资金的时间价值,建立了有限计划期内的易腐品库存模型。Chan等[3]则在允许缺货情况下,研究了零售商关于易腐品的最优运作策略。Manna和Chaudhuri[4]基于需求率和腐败率与时间相关,构建了易腐品库存系统模型,并分别讨论了不允许缺货和允许缺货情况下库存系统的最优决策。苏菊宁等[5]考虑物流时间和随机损失,分析了分散决策和集中决策下生鲜农产品供应链的订货与物流方案。Liang和Zhou[6]在两仓储模型中探讨了零售商在条件延期付款下关于易腐品的最优订货策略。在顾客部分预付条件下,贾涛等[7]分析了两级商业信用对于易腐品库存策略的影响。Ghiami等[8]则研究了易腐品在零售商的自有仓库和租赁仓库中有不同腐败率的情况,并分别考虑易腐品在自有仓库和租赁仓库的腐败成本。
上述一系列易腐品模型均假定产品到达零售商后就开始腐败,然而存在非即时易腐品可以在一定时间内维持自身品质不发生腐败(Wu等[9])。由于在非即时易腐品情境中,零售商可以通过调整订购周期来控制产品在腐败阶段的销售周期长度,因而许多学者也在各种维度下构建了非即时易腐品的库存模型。Ouyang等[10]研究了延时还款下非即时易腐品的最优订货量决策,发现零售商可通过降低订货量,以及提高存储条件等来降低库存成本。Yang和Chang[11]构建了两仓储和允许缺货下关于易腐品的库存模型,并考虑了通货膨胀对零售商订货策略的影响。Tat等[12]考虑了一个供应商和一个零售商组成的供应链系统,并分别在允许或不允许缺货情境中,研究了供应商管理库存下的非即时易腐品库存策略。
事实上,易腐品不仅会发生腐败,而且有保质期约束。即当且仅当在保质期内,易腐品可以用来满足市场需求;而在保质期之后,产品会由于腐败失去使用价值。因而,诸多学者也在将保质期纳入到易腐品的模型构建中。Chen和Teng[13]分析了延期付款下零售商对于有保质期的易腐品的最优订购决策问题。鉴于信用期有可能增加违约风险,Wang等[14]综合了违约风险和产品需求建立具有保质期的易腐品经济订购批量模型,决策买方的最优信用期和订货周期。Wu和Chan[15]研究了有保质期约束的易腐品的两级商业信用模型,该模型假设零售商有较好的商业信誉,因此能得到供应商的全额延时还款待遇。Wu等[16]在具有保质期的易腐品两级商业信用模型中,采用现金流量贴现法分析了所有的相关成本,得出了零售商的最优订货周期。
由于易腐品的腐败特性,有相当一部分产品会在零售阶段失去使用价值。因此,许多学者往往会通过调整零售价格来刺激产品销售量以减少产品腐败量,即基于产品需求与零售价格负相关这一假设来制定零售商关于易腐品或非即时易腐品的最优价格和订购决策。Teng和Chang[17]构建了一个货架展示量有限制的易腐品库存模型,并探讨了需求依赖价格和库存下零售商最优的运作决策。Avinadav等[18]则在需求与价格和时间相关的情境中构建了易腐品的库存决策模型。在需求率与价格和库存水平相关的情形下,Soni[19]则研究了延期付款条件下非即时易腐产品的最优订货策略。在需求依赖价格情境下,Maihami和Karimi[20]考虑了在允许缺货条件下零售商关于非即时易腐品的最优订购和定价策略。
在易腐品的零售阶段,企业不仅需要应对产品腐败造成的数量损失,同时也要考虑产品的保质期特征(货架时间限制)。因而企业通常会在产品的不同阶段(如较为新鲜的阶段和接近保质期的阶段),采用不同的定价决策来调整易腐品的销售速率。例如在易腐品货架周期的后半段,对于未销售的库存产品进行打折促销。而在理论研究中,相关学者会通过假设易腐品以一个恒定的零售价格在零售阶段进行销售,来考虑价格决策对于零售商易腐品订购策略的影响。然而考虑到消费者对于处于不同品质阶段产品的支付意愿,零售商可以考虑对非腐败阶段和腐败阶段的产品实行差异化的价格策略。即针对具有保质期的非即时易腐品,根据其产品品质可划分3个阶段:在非腐败阶段,零售商可以根据消费者对于新鲜产品品质偏好确定最优零售商价格;而在腐败阶段,为了刺激市场需求从而减少产品腐败量,零售商可以降低零售价格以尽快将产品全部售出;而到了保质期之后,由于产品失去使用价值而被舍弃。基于此,本文根据产品需求依赖零售价格假设,首次将保质期和非即时易腐品的概念进行结合,进而分析了零售商的最优订购与定价决策。具体而言,与已有易腐品库存模型相比,本文的创新点包括以下两个方面。
(1)针对具有保质期的非即时易腐品,首次提出了零售商可以通过在非腐败阶段设置较低的零售价格,将易腐品在产品腐败之前完全售出。
(2)基于需求依赖价格的一般化需求函数,首次分析了零售商在非腐败阶段和腐败阶段下最优的差异化定价决策方案。
1 符号表示与基本假设
本文主要采用以下符号表示和基本假设来构建零售商关于有保质期约束的非即时易腐品库存模型。
1.1 符号表示
A:零售商固定订购成本;h单位产品单位时间库存成本;p:在非腐败阶段,单位产品零售价格(决策变量);c:单位产品批发价格,其中c≤p;p0:单位产品零售价格的上限值;δ:在腐败阶段,单位产品零售价格的降价率(决策变量);D(p):产品需求率;θ(t):产品腐败率;td:产品的非腐败阶段长度;m:产品保质期,其中td≤m;T:零售商的订购周期(决策变量);Q:零售商的订购量;Π(p,T,δ):零售商单位时间利润函数。
1.2 基本假设
(1)本文考虑单一零售商关于有保质期约束的非即时易腐品的定价与订购决策问题。
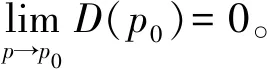

(4)基于非即时易腐品特征,本文借鉴Sarkar[23]的假设,将有保质期约束的非即时易腐品的腐败率定义如下:
(1)
(5)提前期为零且不允许缺货,因此在本文情境中,零售商的产品订购周期等同于其销售周期。
2 模型构建
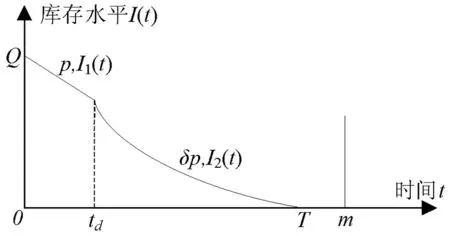
针对有保质期约束的非即时易腐品,零售商有两种订购策略:一种是将易腐品在开始腐败之前就完全售出,从而避免零售阶段产品腐败的发生,即0 情形10 (2) 情形2td≤T≤m。 在情形2中,零售商订购Q单位数量的非即时易腐品。在[0,td]期间,库存水平受产品需求率Dp的影响逐渐下降。而在[td,T]期间,受到产品需求率Dδ和腐败率的共同作用,零售商库存水平将减少直至为0。零售商的库存水平变化示意图可见图1。 图1 零售商库存水平变化示意图 因此,零售商在[0,td]期间库存水平变化可由下列微分方程表示 (3) 根据边界条件I1(0)=Q和式(3),可以得到I1(t)表达式 I1(t)=Q-Dpt, 0≤t≤td (4) 相应的,可知零售商在[td,T]库存水平变化由式(5)决定。 (5) 根据边界条件I2(T)=0和式(5),可得到表达式 (6) 考虑到I(t)的连续性,可以得到I1(td)=I2(td),因此零售商的订购量为 (7) 将式(7)代入式(4),可以得到 Dp(td-t), 0≤t≤td (8) 因此,可知零售商单位时间利润函数包括以下部分: (2)单位时间库存成本 (9) 综合情形1、2,得到考虑有保质期的非即时易腐品零售商的单位时间利润函数 (10) 由于T=td时,Π1(p,td,δ)=Π2(p,td),可知Π(p,T,δ)连续。 本部分,我们将分别分析两种情形下零售商单位时间利润函数Πi(p,T,δ),i=1,2,从而得到零售商的最优定价和订购策略。 情形10 在此情形中,对式(2)的Π1(p,T)分别关于p和T求一阶偏导数,可以得到 (11) (12) (13) 引理1考虑到p∈[c,p0],可知Dp>0和TA>0,且TA随着p的增加而增加。 情形2td≤T≤m。给定p和δ,对Π2(p,T,δ)关于T求一阶偏导数,可得到 (14) (15) (16) 通过分析G(td)和G(m),可得到以下定理。 定理2给定p和δ,对于T∈[td,m], (1)如果G(m)≥0,则Π2(p,T,δ)在T=m取得最大值。 (2)如果G(td)>0和G(m)<0,则Π2(p,T,δ)在唯一驻点T=TB处取得最大值,其中G(TB)=0。 (3)如果G(td)≤0,则Π2(p,T,δ)在T=td取得最大值。 根据定理2可知,当G(td)≤0,零售商会将产品在其非腐败阶段销售完毕,以避免腐败产品对于其运作绩效的消极影响。反之,零售商会延长订购周期,进而继续在腐败阶段销售产品。 类似的,给定p和T,对Π2(p,T,δ)关于δ求一阶和二阶偏导数,可得到以下等式: (17) (19) (20) (21) (i)当H(1)<0,则Π2(p,T,δ)在δ=δB取得最大值,其中H(δB)=0。 (ii)当H(1)≥0,则Π2(p,T,δ)在δ=1在取得最大值。 (iii)当H(1)≥0,则Π2(p,T,δ)在δ=1取得最大值。 根据定理3可知,当p≤Δ3时,零售商会保持产品在腐败阶段的零售价格不变。而当c≤Δ3≤p时,零售商虽有可能在腐败阶段降低零售价格而刺激市场需求,但会避免将零售价格降低至批发价格c。 类似的,给定T和δ,对Π2(p,T,δ)关于p求一阶导,可得到以下等式: (22) 算法: Step2给定单变量边界,求解情形2下的边界解。 Step3给定双变量边界,求解情形2下的边界解。 Step4分别给定δ=1、p=c和T的上下限,可得情形2下的驻点解,即(c,td,1)和(c,m,1)。 在本部分中,将采用不同的需求函数形式分析需求依赖零售价格下,零售商关于具有保质期的非即时易腐品的订购和定价策略。 (1)随着产品市场需求规模的增加,p*和Π*相应增加,T*则相应减小。由于初始市场的规模逐渐扩大,产品的需求也逐渐增加,因而零售商会考虑缩短订购周期,以降低产品腐败损失。同时受到不断上扬的市场需求的刺激,零售商愿意损失部分消费者来提高产品价格p*,以期获取更大的利润。 (2)随着价格敏感系数b的增加,p*和Π*同时减小,T*则相应增加。也就是说,由于产品需求与价格的敏感度的增加,零售商必须通过降低p*来刺激市场需求。但市场需求的增加量不足以弥补产品售价p*减少带来的销售收入下降,因而造成了零售商利润的减少。 (3)产品保质期与p*,T*和Π*均呈正相关。这可以认为是较长的保质期会导致一个相对较低的腐败率,因此零售商可以延长订购周期T*并提高产品售价p*,从而促使自身单位时间利润的上涨。当m较小时,产品腐败率高,零售商会缩短订购周期T*并降低产品在非腐败阶段的定价,使得产品在非腐败阶段出清。 (4)由于产品非腐败阶段时间td的延长,T*和Π*相应增加,p*则相应减小。即由于非即时易腐产品可以在更长的周期内维持产品品质,零售商可以延长订货周期T*并避免产品腐败量的大量增加。特别是当td超过一定数值时(本例中,td≥1.5时),零售商将会缩短订购周期直至小于td,使得产品在非腐败阶段出清。 (5)随着单位产品成本参数的增加(包括库存成本h和批发价格c),可以发现p*相应增加,T*和Π*则相应减小。即零售商会倾向提高单位产品销售价格p*来促进销售收入的增长,进而缓解成本支出对于利润的负面影响。同时,零售商会缩短订购周期T*来减少产品腐败/积压带来的成本上升。 表1 线性需求函数下零售商的最优运作方案 参数p∗T∗δ∗Π∗a14051.441.2412471.6916058.041.1813376.9318064.661.1214416.6120071.291.0915590.4822077.921.0516898.40b0.9115.721.08110022.141.287.951.0817250.751.571.291.0915590.481.860.181.0914485.782.152.251.1013698.56m171.240.9915581.71271.271.0615588.082.571.291.0915590.48371.301.1115592.52571.331.1815598.28td0.2571.480.9215520.380.5071.340.9915562.710.7571.291.0915590.481.2571.291.25/5613.751.571.401.47/5617.24h171.101.2215645.851.671.211.1315611.74271.291.0915590.48471.610.9215496.76872.140.74/5345.44c1.668.131.2216214.206.470.491.1115742.88871.291.0915590.489.672.081.0715440.291273.271.0415219.02 表2 指数型需求函数下零售商的最优运作方案 参数p∗T∗δ∗Π∗α36029.32 1.13 1.00 1484.9372028.81 0.81 1.00 4866.60120028.79 0.79 1.00 5435.16144028.750.75 0.96 6573.93156028.73 0.73 /7144.10β0.0248.750.751.0013922.110.0342.09 0.76 1.00 11051.220.0528.79 0.79 1.00 5435.160.07522.08 0.75 0.80 2786.990.118.75 0.75 /1573.59m128.77 0.77 1.00 5434.831.528.78 0.78 1.00 5434.92228.790.791.005435.052.528.79 0.79 1.00 5435.162.7528.790.791.005435.21td0.6028.730.711.005423.640.7528.79 0.79 1.00 5435.16 128.840.84/5436.811.2528.84 0.84 /5436.811.5028.84 0.84 /5436.81h0.428.260.971.005636.881.628.670.821.005481.17228.790.791.005435.162.829.000.71/5349.69429.200.60/5240.34c424.750.751.006695.966.427.180.781.005909.22828.790.791.005435.169.630.400.801.004997.771232.750.75/4400.51 算例2本算例采用指数型需求函数D(p)=αe-βp,其中α是产品市场需求基准,β是产品需求的价格敏感系数,且p0=+∞。相关参数赋值如下:α=1200,β=0.05,c=8,A=200,h=2,m=2.5和td=0.75。通过上述算法,我们可以知道零售商最优订购周期T*=0.79,最优定价p*=28.79,δ*=1,其最优单位时间利润Π*=5435.16。本算例进一步调整α,β,m和td的数值,分析不同参数值下零售商的最优定价和订购策略以及最优利润。 根据表2中指数型需求函数的计算结果,可以得到以下结论。 (1)产品市场需求基准α与Π*呈正相关,与p*和T*呈负相关。也就是说,当易腐产品初始市场规模逐渐增大,零售商会有动机去降低p*以缩短订购周期,从而刺激市场需求来实现自身利润Π*的增加。当α较大时(本例中,α=1440时),零售商会降低腐败阶段的产品零售价格(即δ*=0.96),降价加速腐败阶段产品出清。特别是当α足够大时(本例中,α=1560时),零售商会进一步调整非腐败阶段定价订购策略,使得产品在非腐败阶段内完全售完。 (2)随着产品需求的价格敏感系数β的增加,p*和Π*同时减少。当需求价格弹性增大时,零售商会通过降低p*刺激需求。当β较小时(本例中,β≤0.05时),零售商将不会下调产品在非腐败阶段的零售价格。而当β较大时(本例中,β=0.075时),零售商会降低腐败阶段时产品的售价(即δ*=0.80),以使产品尽快出清。当β足够大时(本例中,β=0.1时),零售商会降低非腐败阶段价格以便将T*小于td,从而使得产品在非腐败阶段出清。 (3)随着易腐品保质期m的延长,T*,p*和Π*相应增加。即保质期的增加使得产品腐败率的降低,因而零售商可以延长订购周期T*,并逐步提高价格p*从而获取更高的利润。当m足够大时(本例中,m≥2时),由于m远超过零售商的最优订购周期T*,因而不会对最优决策造成进一步的影响。 (4)由于易腐品非腐败阶段td的延长,T*,p*和Π*相应增加。也就是说,由于非即时易腐产品可以在更长的周期内维持产品品质,零售商可以相应延长订货周期来增加销售收入。特别当td足够大(本例中,td=1),零售商可以将最优订购周期T*限制td之内,从而在产品腐败之前实现产品的快速出清。 (5)与线性需求函数类似,在指数型需求函数下,零售商也会增加销售价格p*,缩短订购周期T*,进而应对单位产品成本参数的增加(包括库存成本h和批发价格c)。同时,可以发现当单位产品成本参数增加到一定数值后(在本算例中,h=2.8或c=12),零售商将在td之内把所有产品销售出去,进而避免腐败成本的发生。 对于具有保质期的非即时易腐品,零售商可以在非腐败阶段和腐败阶段进行差异化定价来优化自身的运作策略。即零售商可以通过降价将产品在非腐败阶段销售完毕,或者降低产品在腐败阶段的零售价格来减少腐败损失。基于此,在需求依赖零售价格情境下,本文考虑了零售商关于有保质期约束的非即时易腐品的最优订购和定价策略。并根据由此得到的零售商单位时间利润函数,发现零售商针对有保质期的非即时易腐产品有三种可行的订购与定价策略:i)在产品非腐败阶段,通过设置一个较低的零售价格刺激市场需求,将产品在腐败之前完全售出;ii)在产品进入腐败阶段情形下,零售商降低产品售价以加速产品清仓;iii)非即时易腐品在非腐败和腐败阶段的售价保持不变。借助线性与指数型两种形式的需求函数进行数值算例,可以得到以下管理启示。 (1)当非即时易腐品的初始市场规模逐渐扩大时,零售商可以缩短自身的最优订购周期来减少产品腐败量。特别是在指数型需求函数情境中,零售商可以考虑在产品进入腐败阶段后,降低产品售价以加速产品清仓。 (2)当产品的需求价格敏感系数增加时,零售商会倾向于降低产品零售价格,从而刺激市场需求来增加自身利润。特别是当需求的价格敏感系数较大时(在指数型需求函数下),零售商可以降低非腐败阶段价格以便将产品在非腐败阶段出清。 (3)当易腐品保质期m不断增加时,零售商可以将非即时易腐品在腐败阶段的售价保持不变。同时考虑到产品腐败速率的不断降低,零售商会提高产品定价来增加销售收入,并延长订货周期来提升自身利润。 (4)当产品非腐败阶段td较短时,零售商会将非即时易腐品在非腐败和腐败阶段的售价设为相同。而当产品非腐败阶段td不断增加时,零售商更更倾向将最优订购周期T*限制td之内,从而在易腐品开始腐败之前将产品完全售出。 (5)随着单位产品成本参数的增加(包括库存成本h和批发价格c),零售商会考虑增加销售价格p*和缩短订购周期T*,来减少库存成本或购买成本对于销售利润的负面影响。






3 理论分析

















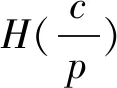


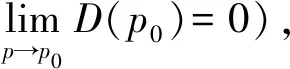


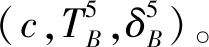
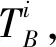




4 数值算例
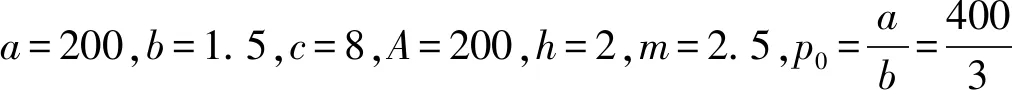


5 结论
