基于Pythagorean模糊非线性规划及其在群决策中的应用

朱敦赣

(集美大学理学院，福建 厦门 361021)

0 引言

1965年，Zadeh[1]首次提出模糊集理论。以此为基础，相关学者对模糊集进行了一步步优化，其中最具代表性的是直觉模糊集[2]和Pythagorean模糊集[3]。在现有的多属性决策问题中，决策者对备选方案在各属性下评价越来越模糊，使得多属性决策问题的难度也随之加大。而直觉模糊集和Pythagorean模糊集的出现，恰恰可以解决很多类似的决策问题。

Yager[2]于2014年提出Pythagorean模糊集。与直觉模糊集不同的是，Pythagorean模糊集将其隶属度和非隶属的取值范围从隶属度与非隶属度之和小于等于1拓展至隶属度与非隶属度的平方和小于等于1，隶属度和非隶属度取值范围的扩大，给决策者评价的精确性提供更多保障。Pythagorean模糊集现已被广泛应用于风险的评估[4]、投资[5]、模式识别以及医疗诊断[6]等方面。

目前，基于Pythagorean模糊集的决策方法相关研究已经取得了一些研究成果：刘卫峰等[7]定义了Pythagorean模糊数的交叉影响运算法则，并提出几种Pythagorean模糊信息集成算子和基于Pythagorean模糊交叉影响集成算子的决策方法；丁恒等[8]针对Pythagorean模糊环境下的多属性群决策问题，提出 Pythagorean模糊幂加权平均算子，研究所提出算子的基本性质，并提出基于PFPWA算子的群决策方法。但是以上研究多是基于集成算子的研究方法，由于集成算子公式构造的多样性，容易给评价结果造成误差，致使最终获得的最优方案存在争议。所以，本文将Pythagorean模糊集与最优化理论相结合，减少人为主观方面的影响，以使最终的评价结果更加精确。

在多属性群决策过程中，因为需要考虑多个决策的评价信息，首先需要确定决策者的相关权重，然后再将这些决策个体给出的评价信息通过信息集成的方式得到综合决策信息，所以在群决策过程中，确定决策者的权重就显得尤为重要。文献[9-11]从决策者的主观权重和客观权重出发，给出了确定决策者权重的几种方法。文献[12]给出将决策者主观权重和客观权重组合为决策者的最终权重的方法。解决多属性群决策问题的另一个重要的影响因素是属性权重的确定。在属性权重信息完全未知且属性值为实数的情况下，可采用加权平均法[13]、方差最大化法[14]、信息熵法[15]等。由于其评价的客观性以及专家在某些未知领域知识的局限性，多数评价值现被以模糊数的形式给出，所以以上针对实数的属性权重值的确定方法已经不足以解决该类问题，使得基于模糊评价值的多属性群决策问题成为了现阶段研究的热点方向。

本文主要研究在Pythagorean模糊环境下的多属性群决策问题，提出了一种基于Pythagorean模糊非线性规划的多属性群决策方法。首先,引入关于模糊集的一系列基本概念;其次,针对Pythagorean模糊非线性规划多属性决策问题,给出两种思路下决策者和属性客观权重的确定方法,同时给出Pythagorean模糊非线性规划模型;最后,以航空公司机型的选取为背景,实例论证了模型的可行性和有效性。

1 基本概念

定义1[1]设X为一论域,X上形如A={〈x,μA(x)〉|x∈X}的二元组被称为X上的一个模糊集,其中μA(x)∈[0,1],它代表x隶属于A的程度,简称隶属度,记a=μa为一个模糊数(FN)。

定义2[2]设X为一论域,X上形如A={〈x,μA(x),νA(x)〉|x∈X}的三元组被称为X上的一个直觉模糊集,其中μA(x)∈[0,1],νA(x)∈[0,1],且μA(x)+νA(x)≤1。μA(x)为隶属度，νA(x)为非隶属度。令πA(x)=1-μA(x)-νA(x),称πA(x)为犹豫度,故πA(x)∈[0,1]。记a=(μa,νa)为一个直觉模糊数(IFN)。

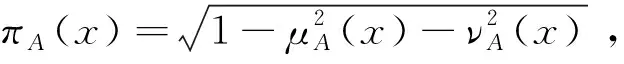
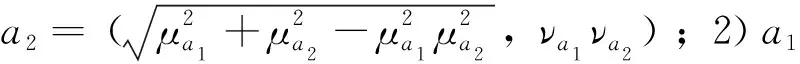
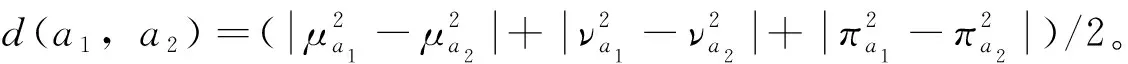
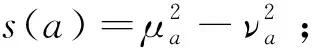
定理1[3]设a1,a2为两个Pythagorean模糊数,若：1)s(a1)>s(a2),则a1>a2；2)s(a1)=s(a2),有：若h(a1)>h(a2),则a1>a2;若h(a1)=h(a2),则a1=a2。

2 基于Pythagorean模糊非线性规划的群决策权重确定模型

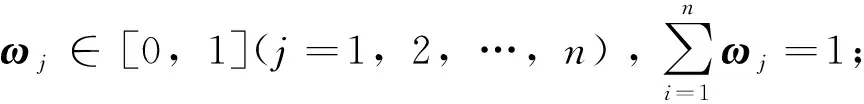
假设决策者用Pythagorean模糊数做决策评价,记决策者ek的评价矩阵Sk=(sij(k))m×n(k=1,2,…,l),其中sij(k)代表决策者ek对方案pi在属性qj下的评价,现假设属性权重ω和决策者权重W完全未知,试通过确定方案优先排序。

将决策者ek的评价矩阵Sk=(sij(k))m×n(k=1,2,…,l)规范化为Rk=(rij(k))m×n(k=1,2,…,l),对于效益型属性对应的评价值不需作任何变动,对于成本型属性对应的评价值,取其补来替代,即

(1)

2.1 基于非线性规划的群决策专家权重确定模型

对于决策者ek,es,其决策者权重分别为wk,ws,先计算两个矩阵加权之后对应元素的距离之和,简称加权决策矩阵距离,记为：

(2)

再计算两两决策者之间的加权决策矩阵距离之和,记为：

(3)

最后求解目标规划：

(4)

得：W={w1,w2,…,wl}。

另一种确定决策者客观权重的方法如下。

对于决策者e1,e2,…,el,其决策者权重对应为w1,w2,…,wl,将决策矩阵R1,R2,…,Rl加权求和,得综合决策矩阵R=(rij)m×n,其中：

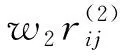
(5)

再计算每个决策矩阵与综合决策矩阵的矩阵对应元素距离之和,记为：

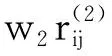
(6)

最后求解目标规划：

(7)

得：W={w1,w2,…,wl}。

2.2 基于非线性规划的群决策属性权重确定模型

在决策者的决策权重W={w1,w2,…,wn}已知的情况下,根据式(3)求得综合决策矩阵R,将综合决策矩阵的属性列加权平均,计算出综合属性列T={t1,t2,…,tm},其中

ti=ω1ri1⊕ω2ri2⊕…⊕ωnrin。

(8)

再计算综合决策矩阵的每一属性列与综合属性列的对应元素距离之和,记为：

⊕ω2ri2⊕…⊕ωnrin,rij)。

(9)

最后求解目标规划：

(10)

得：ω={ω1,ω2,…,ωn}。

3 基于Pythagorean模糊非线性规划的群决策方法

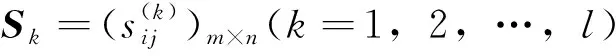
步骤2：利用式(2)～式(4)求解决策者的客观权重向量W={w1,w2,…,wn}。

步骤3：通过式(5),求得综合决策矩阵R。

步骤4：利用式(8)～式(10)求解方案属性的客观权重向量ω={ω1,ω2,…,ωn}。

步骤5：通过式(8)计算综合属性列T={t1,t2,…,tm},并根据定义6及定理1求得各方案对应的得分函数和精确函数。

步骤6：排序和择优。

4 实例分析

4.1 问题背景

随着我国经济的高速运转,我国的民航事业也得到了持续和稳定的发展,尤其自国家允许民营资本进入市场以来,多家民营航空公司相继问世,并迅速扩张市场。在多家航空公司激烈竞争的背景下,航空公司成立和发展过程中不可避免存在的问题就是飞机的机型选择问题。机型选择作为航空公司重要的战略规划之一,直接决定了航空公司的长期经济效益,而且还在一定程度上影响公司的技术、管理水平及其市场竞争力。

德国戴姆勒-克莱斯勒宇航公司(DASA)对全世界航空公司选购飞机的关键因素进行了分析研究,为航空公司提供相应的经济和运营指标,主要包括：经济性,飞机性能,通用性,环保性以及舒适性。随着旅客出行次数增加,对航空出行的深入了解,旅客出行行为逐渐改变,在航空出行时对机型、航空公司等方面有更多的要求。航空公司在进行机型选择时,不仅需要考虑旅客对机型的选择的偏好,还需要从旅客的安全、舒适性等角度考虑。因此,对航空公司机型选择的研究可以有效地分析旅客对机型的舒适性和品牌的要求,并能够给航空公司带来更多的收益。

4.2 实例分析

现考虑一个航空公司机型选择问题。假设现在有3个机型P1,P2,P3可以选择,针对这些机型选择需要考虑5个方面的内容：1)舒适度(Q1);2)飞机性能(Q2);3)环保性(Q3);4)通用性(Q4);5)价格(Q5)。其中Q1,Q2,Q3,Q4均为效益型属性,只有Q5属于成本型属性。现航空公司聘请了3位专家e1,e2,e3来对3种机型在5个方面进行评价,3位专家给出的初始评价矩阵如表1。

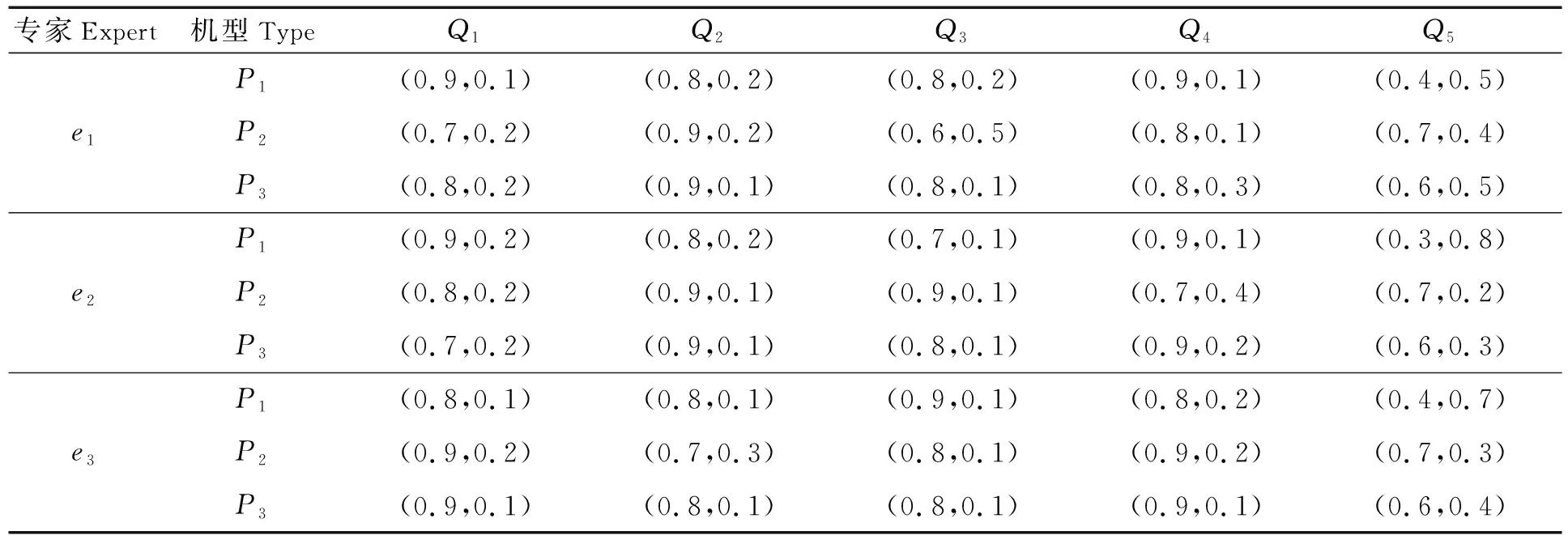
表1 专家e1,e2,e3给出的Pythagorean模糊评价矩阵S1

步骤1 根据式(1)将3位专家的初始评价矩阵规范化并计算其犹豫度,得规范化后的评价矩阵如表2。

表2 专家e1,e2,e3的规范化评价矩阵R1

步骤2 根据式(2)～式(4),解得专家客观权重向量为：W=(0.333 6,0.333 3,0.333 1)。

步骤3 已知专家客观权重向量,再由式(5)计算出综合的专家评价矩阵如表3。

表3 专家e1,e2,e3的综合评价矩阵R

步骤4 根据式(8)～式(10),求解得方案属性的客观权重向量为：ω=(0.1886,0.1679,0.1461,0.1886,0.3088)。

步骤5 已知属性客观权重,再通过式(8)计算方案的综合属性列T,并根据定义4计算出3个方案综合评分值的得分函数和精确函数,如表4。

表4 3个方案的综合属性评价表

步骤6 排序和择优。根据定义6和定理1,比较3个方案综合属性评价值的大小,得出3个方案的优先排序方案,结果为：P1>P2>P3。故综合5个方面的考虑,航空公司应选择第一种机型。

5 结语

本文提出了一种基于Pythagorean模糊非线性规划的多属性群决策方法。首先,针对Pythagorean模糊非线性规划多属性决策问题,给出两种思路下决策者和属性客观权重的确定方法,进而提出此类模糊群决策的详细解决步骤;其次,以航空公司机型的选取实例，论证了本文提出的Pythagorean模糊非线性规划的多属性决策模型的可行性和有效性。

本文运用的矩阵间距离测度公式的定义仅基于Lance距离进行的拓展，而且简单的平方差会增加评价误差。同时，目标函数的模型构造也较为简洁。下一步的工作目标就是在本文的基础上改进距离公式和目标函数，以提高评价的精确度。