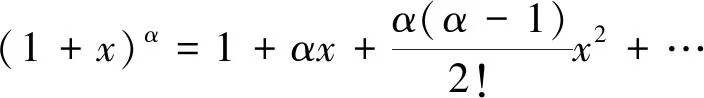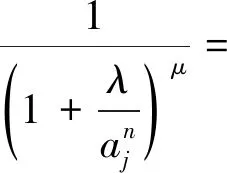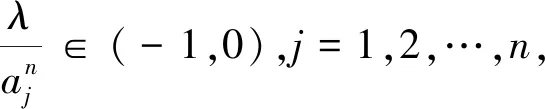两个猜想不等式的证明与推广*
2019-06-11石冶郝
石冶郝 林 玲 孙 颖
(1. 首都师范大学初等教育学院, 北京 100048; 2. 湖南省邵阳市大祥区祥凤实验学校, 湖南 邵阳 422000)
0 引 言
李阳刚[1]从一道奥林匹克问题入手,利用柯西不等式及均值不等式得到一类不等式的统一证法,并提出两个类似不等式的猜想. 为下文需要,先给出参考文献[1]的两个定理和两个猜想.
定理A设a,b>1,-1≤λ≤1,则
(1)
定理B若a1,a2,…,an>1,n∈N+,n≥2,0<λ≤1,则
(2)
猜想1若a,b,c>1,0<λ≤1,则
(3)
猜想2若a1,a2,…,an>1,n∈N+,n≥2,0<λ≤1,则
(4)
本文利用函数的凹凸性,借助琴生不等式,给出了不等式(1) 和(2)的更一般的形式,在特殊情形下,上述两个猜想得到了证明.
1 主要结论
定理1若a1,a2,…,an>1,n∈N+,-1≤λ≤1,则当μ≥1时,
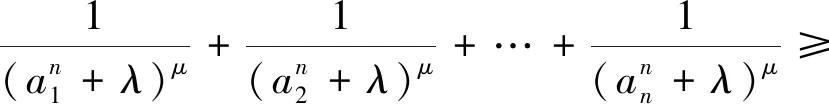
(5)
等号成立当且仅当a1=a2=…=an.
定理2若0 (6) 等号成立当且仅当a1=a2=…=an. 定理1和定理2证明方法相似,下面仅给出定理1的证明. 当μ≥1时,且-1≤λ≤1,x>0,则f″(x)>0. 注1当μ=1时,由定理1的特殊情形容易发现参考文献[1]的猜想2是成立的,显然猜想2是猜想1的高维情形,因而猜想1自然成立. 但是定理1拓广了两个不等式(3) 和(4)中参数λ的研究范围. 注2下面给出不等式(3)的一种加细. =f(lna3)+f(lnb3)+f(lnc3) 故有 高维情形类似可得加细不等式. 为确认SL-ASIA量表测量的有效性,本文将3个村寨获得的样本按各村寨人数比例随机分成人数基本相同的两组(Ecklund,2005;Reynolds,Ecklund &Terrance,2011)。使用一组样本借助探索性因子分析检验侗寨原住民的文化适应情况及内在维度,使用另一组样本借助验证性因子分析来交叉验证第一组样本里提出的维度模型,以观察和确认派生出的各个维度的内部一致性。 注3当μ≥1时, 如果事先用数学归纳法证明了猜想2,但是数学归纳法证明过程非常繁琐,则可根据不等式(2) 、(4)和幂平均不等式有 因此 整理即得定理1.利用Jensen加权不等式, 可以对定理1和定理2作加权推广. 定理3若ak>1,ωk∈(0,1),k=1,2,…,n,ω1+ω2+…+ωn=1,n∈N+, -1≤λ≤1, 当μ≥1时, (7) 等号成立当且仅当a1=a2=…=an. 定理4若ak∈(0,1],ωk∈(0,1),k=1,2,…,n,ω1+ω2+…+ωn=1,n∈N+,λ≥1, 则当0<μ≤1时, (8) 等号成立当且仅当a1=a2=…=an. 下面给出定理3的证明. 利用Jensen加权不等式, 得ω1f(lnx1)+ω2f(lnx2)+…+ωnf(lnxn)≥f(ω1lnx1+ω2lnx2+…+ωnlnxn), 同理可证定理4. 定理5若λ>0,n∈N+,ω1+ω2+…+ωn=1,ωk∈(0,1),k=1,2,…,n, (1)当μ∈(-∞,0)时,xk∈(0,+∞) ,则 (9) (10) (11) 等号成立当且仅当x1=x2=…=xn.证明过程从略. (12) (11)退化为: (13) 不等式(5)与(12),(6)与(13)比较,结构相同,但是不等式中的变量约束条件和参数范围不一致. 本文对λ<0的情形不再讨论. 回顾定理1和定理2,当λ=1且μ=1时,即成为Henrici′s不等式[2]: 等号成立当且仅当a1=a2=…=an. 同时,本文所证定理的一些特殊情形也频繁的出现在数学竞赛关于不等式证明的试题中,利用定理1(当λ=1且μ=1时)和定理4,分别得到下面3个例题. 例1(第39届IMO预选试题) 令实数r1,r2,…,rn≥1,试证 说明:本题也可以用数学归纳法证明. 不等式是数学的重要组成部分,它遍及数学的每一个分支学科,在竞赛数学中占有不可忽视的一席之地. 命题者可以根据本文的结论编制不同的数学问题,为不同层次的学生提供方法. 若定理1中参数λ为负数,我们可以用级数方法重新证明不等式(5). 根据二项式函数(1+x)α的幂级数展开式[4], 当α≤-1时, 收敛域为(-1,1). 因此,当μ≥1时, 于是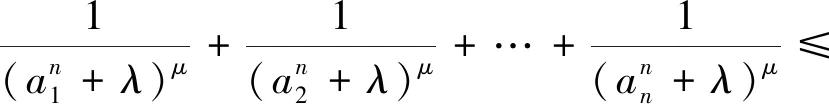
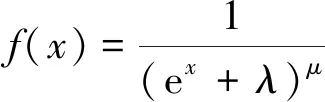
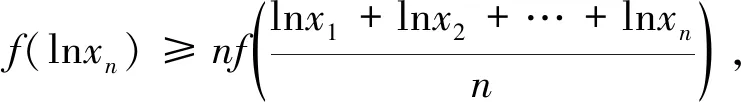
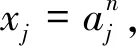
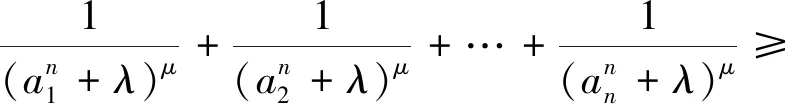
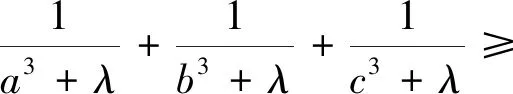
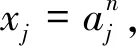

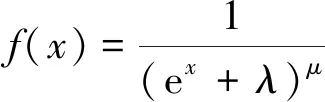
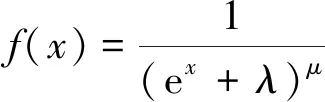
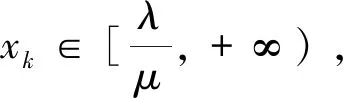
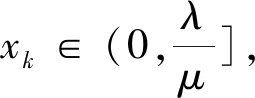
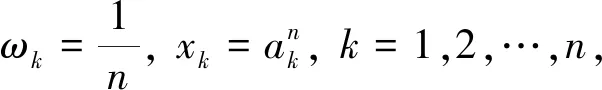
2 应 用
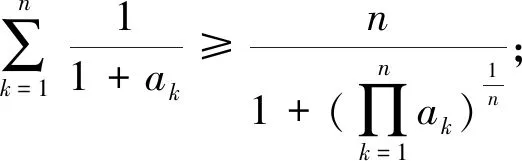
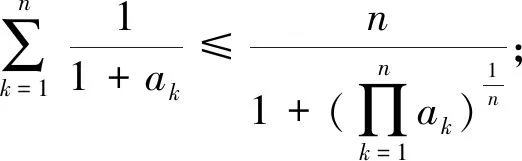
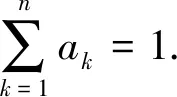
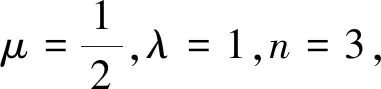
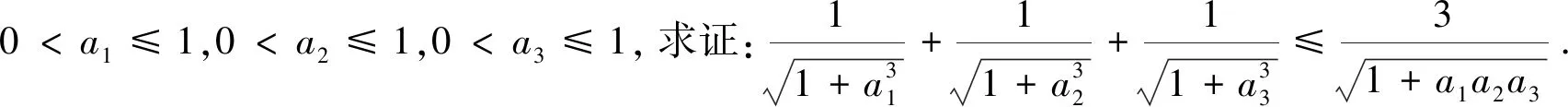
3 思 考