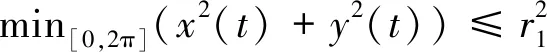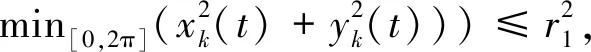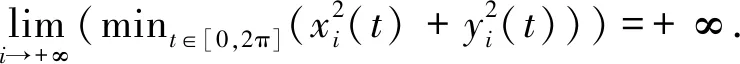具有不对称非线性项平面系统周期解的存在性*(下)
2019-06-11马田田
马 田 田
(首都师范大学,北京 100048)
4 主要引理的证明
x(t)=r(t)cosθ(t),y(t)=r(t)sinθ(t).
通过极坐标变换,系统(3.1)变形为
(3.2)
这里p1(t,r,θ)=p1(t,rcosθ,rsinθ),p2(t,r,θ)=p2(t,rcosθ,rsinθ). 令
(r(t),θ(t))=(r(t,r0,θ0),θ(t,r0,θ0))
表示系统(3.2)满足初始条件r(0,r0,θ0)=r0,θ(0,r0,θ0)=θ0的解,其中x0=r0cosθ0,y0=r0sinθ0.
接下来,引进旋转数的定义. 假设(x(t),y(t))是系统(3.1)的一个2π周期解,且对任意t∈[0,2π],有x(t)2+y(t)2≠0, 其相应的极坐标表示为(r(t),θ(t)). 定义 (x(t),y(t))的旋转数为

4.1 引理3.4的证明
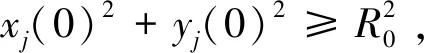

使得
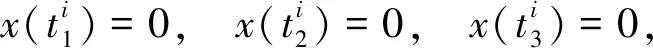
和
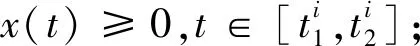

x*=x(t*)=max{x(t)∶α≤x(t)≤β}.
因为x′(t*)=0, 所以f(y(t*))+λp1(t*,x(t*),y(t*))=0. 根据条件(h4), |f(y(t*))|≤M0. 由(h2)、(h3)可知存在d1>0使得|y(t*)|≤d1. 根据(h2)可知f(y)在区间[-d1,+∞)上是有下界的,而由(h3)可知f(y)在区间(-∞,d1]上是有上界的. 因此, 存在η>0使得
f(y)≥-η,y∈[-d1,+∞);f(y)≤η,y∈(-∞,d1].
(3.3)
下面估计t*-α. 选取常数M>M0(M0是条件(h4)中的常数).令
显然,M1>M0. 由(h1)可知存在d2>0使得
sgn(x)g(x)≥M1, |x|≥d2.
(3.4)
定义W+∶R2→R,
W+(x,y)=F(y)+G(x)+M(x-y).
记
W+(t)=F(y(t))+G(x(t))+M(x(t)-y(t)).
则有
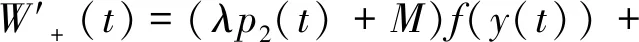
若x(t)≥d2,y(t)≥-d1, 则由(h4), (3.3)和(3.4)可得

从而当(x(t),y(t))位于区域{(x,y)∈R2∶x≥d2,y≥-d1}中时,W+(t)是递增的. 取tα∈(α,t*),tβ∈(t*,β)使得
x(tα)=d2,x(t)≥d2,t∈(tα,t*),
及
x(tβ)=d2,x(t)≥d2,t∈(t*,tβ).
因为y′(t)=-g(x(t))+λp2(t,x(t),y(t)), 所以由条件(h4)和(3.4)可知当t∈[tα,t*]时,有y′(t)≤0. 进而,y(t)≥y(t*)≥-d1,t∈[tα,t*]. 这样,当t∈[tα,t*]时, 有
W+(t)≤W+(t*).
因此,
F(y(t))+G(x(t))+M(x(t)-y(t))≤F(y(t*))+G(x*)+M(x*-y(t*)).
由于|y(t*)|≤d1, 故存在常数B1>0使得|F(y(t*))|≤B1. 进而可知
F(y(t))-My(t)≤[G(x*)-G(x(t))]+M[x*-x(t)]+B1+Md1.
(3.5)
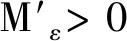
(l+-ε)y-Mε≤f(y)≤(l++ε)y+Mε,y≥-d1,
及
(3.6)
由(3.5)和(3.6)可得当t∈[tα,t*]时, 有
(l+-ε)y2(t)-2(M+Mε)y(t)≤2[G(x*)-G(x(t))]+2M[x*-x(t)]+B2,
这里B2=2(Mε′+B1+Md1). 因此,可得
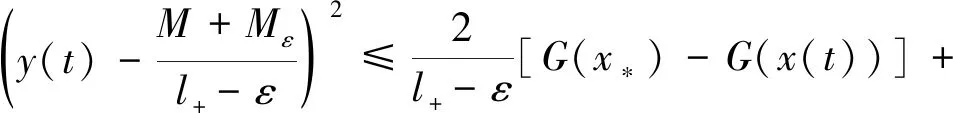
故当t∈[tα,t*]时, 有
y(t)≤
注意到x′(t)=f(y(t))+λp1(t,x(t),y(t)), 由(h4)可知当t∈[tα,t*]时, 有
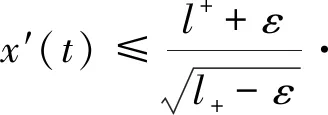
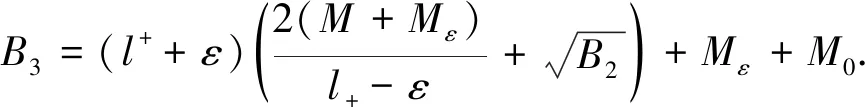

(3.7)
由(h1)可以推出当x*→+∞时,

故有
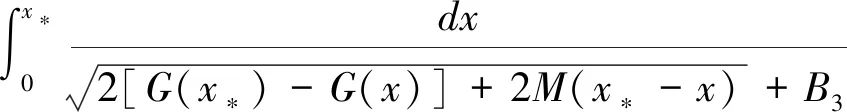
+o(1).
取一个正常数K. 记
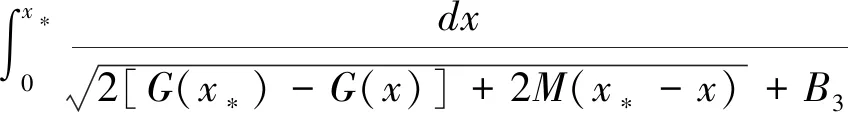
其中
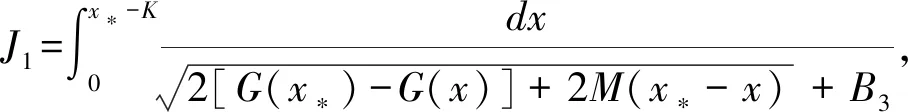
若x∈[0,x*-K],则当x*充分大时, 有
G(x*)-G(x)+M(x*-x)≥G(x*)-G(x*-K)+MK=[g(ξ1)+M]K→+∞,x*→∞,
这里ξ1∈[x*-K,x*].因此,当x*→+∞时, 有
若x∈[x*-K,x*], 则有
G(x*)-G(x)+M(x*-x)=[G(x*)+Mx*]-[G(x)+Mx]=[g(ξ2)+M](x*-x)≥μ(x*)(x*-x),
其中ξ2∈[x*-K,x*],μ(x*)=min{g(x)+M∶x*-K≤x≤x*}. 显然,μ(x*)→+∞,x*→+∞. 从而,可得


易知
根据Ji(i=1,2)的渐近性可知当时x*→+∞, 有

(3.8)
由[6]中的引理4和条件(τ0)可得
(3.9)
由(3.7),(3.8)和(3.9)可知当x(t*)→+∞时, 有
接下来估计tα-α. 因为0≤x(t)≤d2,α≤t≤tα,故由引理3.2可知当x*→+∞时, 有min{y(t)|α≤t≤tα}→+∞, 进而,cα=min{f(y(t))|α≤t≤tα}→+∞.
对等式x′(t)=f(y(t))+λp1(t,x(t),y(t))两边在区间[α,tα]上取积分,可得

因此,
(cα-M0)(tα-α)≤d2.
于是,当x*→+∞时, 有
tα-α=o(1).
这样,就证明了当x*→+∞时, 有
下面估计β-t*.定义函数W-∶R2→R,
W-(x,y)=F(y)+G(x)+M(x+y).
令
W-(t)=F(y(t))+G(x(t))+M(x(t)+y(t)).
则有
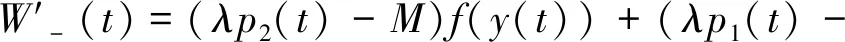
若x(t)≥d2,y(t)≤d1, 则由(h4),(3.3)和 (3.4)可得
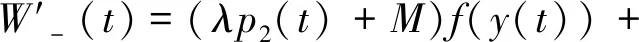
由此可知当(x(t),y(t))位于区域{(x,y)∈R2∶x≥d2,y≤d1}中时,W-(t)是递减的. 应用估计t*-α的方法,可以推得
因此,当x*→+∞时, 有
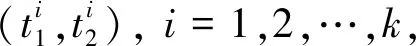
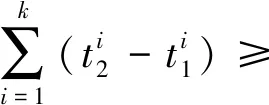
应用同样的方法可以推得

故有

令ε→0, 可得
4.2 引理3.5的证明
沿用证明引理3.5时的记号, 先估计β-α. 定义U+∶R2→R,
U+(x,y)=F(y)+G(x)-M(x-y).
令
U+(t)=F(y(t))+G(x(t))-M(x(t)-y(t)).
若x(t)≥d2,y(t)≥-d1,则由(h4),(3.3) 和 (3.4) 可得

≤(M+M0)η+(M0-M)g(x(t))+2MM0≤0.
因此,当(x(t),y(t))位于区域{(x,y)∈R2∶x≥d2,y≥-d1}中时,U+(t)是递减的. 从而,当t∈[tα,t*]时,
U+(t)≥U+(t*).
由此可知当t∈[tα,t*]时,
F(y(t))+G(x(t))-M(x(t)-y(t))≥F(y(t*))+G(x*)-M(x*-y(t*)).
(3.10)
根据引理3.5的证明可知存在一个常数B1>0使得|F(y(t*))|≤B1. 由(3.10)可得
F(y(t))+My(t)≥(G(x*)-G(x(t)))-M(x*-x(t))-M1,t∈[tα,t*],
(3.11)
这里M1=B1+Md1. 对充分小的0<ε
(l+-ε)y-Mε≤f(y)≤(l++ε)y+Mε.
(3.12)
进而,存在M2>0使得当y≥-d1时,
(3.13)
于是,由(3.11)和(3.13) 可推出当t∈[tα,t*]时,
(l++ε)y2(t)+2(M+Mε)y(t)≥2(G(x*)-G(x(t)))-2M(x*-x(t))-2(M1+M2).
故有

(3.14)
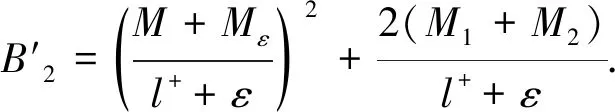
G(x*)-G(x(t))-M(x*-x(t))
=[G(x*)-Mx*]-[G(x(t))-Mx(t)]
≥[G(x*)-Mx*]-[G(x*-L)-M(x*-L)]
=[G(x*)-G(x*-L)]-ML
=[g(ξ)-M]L→+∞, 当x*→+∞,
(3.15)
这里ξ∈[x*-L,x*]. 因此,存在常数C1>0使得当x*≥C1并且x(t)∈[d2,x*-L]时,
(3.16)
由(3.14)和(3.16)可知当x(t)∈[d2,x*-L]时, 有
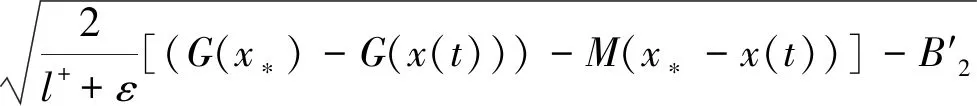
因为x′(t)=f(y(t))+λp1(t,x(t),y(t)),所以由 (3.12)可推得


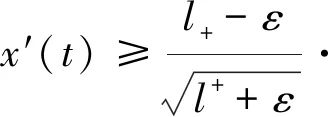
令t1∈[tα,t*]使得x(t1)=x*-L.则可得

由(3.15)和[6]中引理4可知当x*→+∞时, 有
因此,当x*→+∞时, 得到
(3.17)
接下来,估计t*-t1. 对等式x′(t)=f(y(t))+λp1(t,x(t),y(t))两边在区间[t1,t*]积分可得
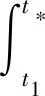
故有
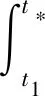
另一方面, 由(3.12)可知
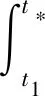
从而,
(3.18)
对等式y′(t)=-g(x(t))+λp2(t,x(t),y(t))两边在区间[t,t*](t∈[t1,t*])上积分, 可得

这里ν(x*)=min{g(x)|x∈[x*-L,x*]}. 显然,当x*→+∞时,ν(x*)→+∞. 因此,
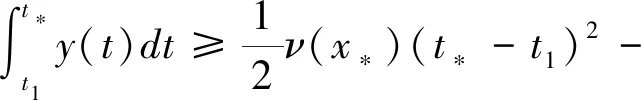
(3.19)
根据(3.18)和(3.19)可知当x*→+∞时,
t*-t1=o(1).
结合(3.17)可得

由引理3.5的证明可知tα-α=o(1),x*→+∞. 因此, 得到当x*→+∞时, 有
为了估计β-t*, 引进另一个函数U-∶R2→R,
U-(x,y)=F(y)+G(x)-M(x+y).
令
U-(t)=F(y(t))+G(x(t))-M(x(t)+y(t)).
若x(t)≥d2,y(t)≤d1,则由(h4), (3.3)和(3.4)可得

-η(M0+M)+g(x(t))(M-M0)-2M0M≥0.
由此可知当(x(t),y(t))位于区域{(x,y)∈R2∶x≥d2,y≤d1}中时,U-(t)是递增的. 应用估计t*-α的方法, 可以得到当x*→+∞时, 有
因此,
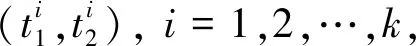
类似地,可以推得
于是, 当x*→+∞时, 有

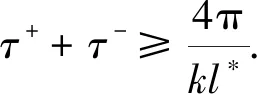
5 定理1.1的证明
只需验证连续性定理2.1的4个条件都满足即可,分4步进行验证.
(1) 存在常数D>0使得若(x(t),y(t))是系统
x′=f(y),y′=-g(x)
(4.1)
的任意2π周期解,则有
x2(t)+y2(t)≤D2,t∈[0,2π].
事实上, 系统(4.1)的首次积分可以表示为
Γc∶F(y)+G(x)=c,
这里F(y),G(x)是在第三节中定义的函数,c是一个任意常数. 易知当c>0充分大时,Γc一条围绕原点的星型闭曲线. 对充分大的c, 用(xc(t),yc(t))表示系统(4.1)位于曲线Γc的周期解,其最小周期记为T(c). 由引理3.5和引理 3.6的证明 (λ=0的情形)可知对任意充分小的ε(0<ε
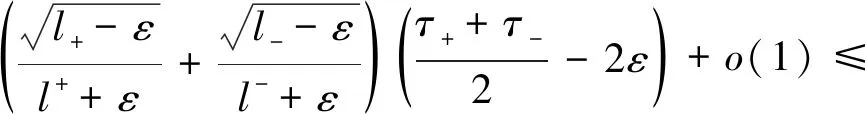
根据条件(τ0)可以取充分小的ε使得当c充分大时,有
设(x(t),y(t))是位于曲线Γc的一个2π周期解, 则存在一个整数k>0使得kT(c)=2π. 从而,n (2) 定义F∶R3×[0,1]→R2, F(t,x,y;λ)=(f(y)+λp1(t,x,y), -g(x)+λp2(t,x,y)). 则有 F(t,x,y;0)=(f(y),-g(x))F(x,y) F(t,x,y;1)=(f(y)+p1(t,x,y), -g(x)+p2(t,x,y)). 由(h2)、(h3) 可得 (4.2) 根据(4.2)和(h1)可推出当r充分大时,d(F,B(0,r),0)=1. (4.3) 由(τ0)可知 (4.4) 由(4.3)和(4.4)可得n 注记4.1定理1.2可以用类似证明定理1.1的方法证明. 事实上, 在定理1.2的条件下, 连续性定理2.1的前3个条件任然成立. 由引理3.4和条件(τ1)可证得条件(4)也成立. 因此,连续性定理2.1的4个条件都成立,从而, 系统(1.1)至少存在一个2π周期解.