遥感影像并行处理的数据划分及其路径优化算法

方 雷，姚申君，包航成，康俊峰，刘 婷

1. 复旦大学环境科学与工程系，上海 200438； 2. 华东师范大学地理科学学院，上海 200241； 3. 金华市规划与地理信息中心，浙江 金华 321000； 4. 江西理工大学建筑与测绘工程学院，江西 赣州 341000； 5. 杭州师范大学理学院，浙江 杭州 311121

海量空间信息处理和应用具有信息密集和运算密集的特征，目前广泛依赖于并行技术和高性能计算机的应用。遥感影像处理(如影像的校正、配准、识别)是并行技术在空间信息处理领域的一大主要应用。早在10年前，国内外就已广泛开展图像的并行化处理研究[1-10]，在该领域取得多方面的成果。例如，结合并行技术和遗传算法有学者提出利用低分辨率相机获取高分辨率图像的方法[6]；部分研究人员提出能高效实现遥感图像预处理的分布式共享存储并行处理系统[7]、遥感卫星图像几何粗校正的数据并行方法[8]、基于小波的遥感图像全局配准算法[9]、遥感多图像配准中自动提取特征点的并行算法[10]、基于GPU的并行算法[11-12]等，此外还有针对遥感影像识别、分割、分类、融合等高性能算法[13-18]。针对数据量呈指数增长的全球遥感图像，必须研究基于并行化的快速、有效、高精度的自动图像配准算法，为此，有学者提出了相应的遥感图像自动配准的并行策略[19-20]。而随着遥感影像并行化方法的研究深入，近5年来，越来越多的学者不满足于某一类操作或者数据的并行化处理算法，而倾向于提出并行算法的通用模型[21-24]。

可以看出，目前研究主要还是利用遥感图像的矩阵可分解性质，设计了大量关于影像并行算法和并行处理的环境。但是，在云计算环境下，一份遥感数据存在多个冗余备份，具备同步并行处理多个计算任务，解决了对一份数据处理时输入输出(I/O)资源争用的问题。例如，可以同时对同一份遥感数据的不同备份进行数据划分和压缩操作，快速生成金字塔索引。过往并没有针对该环境的最佳并行处理路径选择的深入研究。本文在总结前人研究的基础上，给出一个一般情况下的基于数据划分的最佳并行处理路径的数学模型，实现了在相同的遥感影像处理算法和同等的计算资源条件下，计算机自主选择最优处理路径，达到最优的遥感影像处理效率。

1 基于数据划分的最佳并行处理路径的数学模型

并行分为功能分解和数据分解。基于数据分解的并行处理，在遥感图像的并行处理中使用较为普遍。例如，创建金字塔索引时，对原始影像划分的过程中同时伴随着数据压缩。本文根据栅格数据的可分解性给出栅格影像数据并行处理的相关定义，最后提出最佳并行处理路径选择算法的数学模型，即旋转门模型。

1.1 并行处理算法数学模型及其相关定义

一般的栅格影像划分存储及并行处理过程均可以抽象成如图1所示的模型。它包含以下4个要素：数据态Ri、元素个数ni、相对信息量rj、映射f及其对应的单位信息量下的计算代价φp。

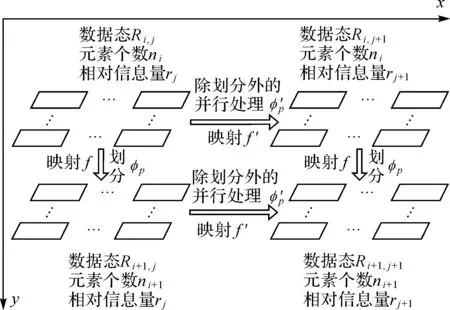
图1 栅格影像的一般并行处理过程Fig.1 General parallel processing model of a raster image

如果要想从源数据态Ri, j生成3个数据态(Ri, j+1、Ri+1, j和Ri+1, j+1)必须经过一次f和f′操作以及一次Ri, j到Ri+1, j的操作；或一次f′和f操作以及一次Ri, j到Ri, j+1的操作。这两次操作可以是串行的操作也可以是并行的操作。任何一条独立的处理链无法同时(并行的)获得3个结果数据态，所以并行操作必须将图中x方向和y方向的操作相结合，形成多路并行处理过程：既生成3个结果数据态，又可以充分利用云计算平台中的多个计算节点的计算资源，提高数据处理效率。此外，虽然有两条处理路径均能生成数据态Ri+1, j+1，但是这种情况在实际的并行过程中显然是不被允许的，因为该方式造成了计算资源的浪费。于是对并行模型进行化简，得到纵向并行和横向并行。

图2给出了更为一般的纵向并行和横向并行处理，显示了从源数据态经过处理链得到的不同的数据态(划分数据态和其他数据态)的过程。图2(a)和(b)均是一个不完全二叉树。易知，不完全二叉树上的每一个分叉都表示一种实行并行的可能性。若将每一个映射过程视为一个并行任务，则并行维数为d的映射过程，可以形成d条并行的子任务。若生成所有的数据态，均有横向并行和纵向并行两种并行路径的选择。易知，若映射f不发生变化，并行路径不发生改变。在具体的并行处理实施过程中，如何让计算机根据映射f动态选择最佳的并行路径将是“遥感影像并行处理并对处理后的数据进行分布式存储，再对存储后的遥感影像进行下一次的并行处理”这种循环往复操作的关键问题。

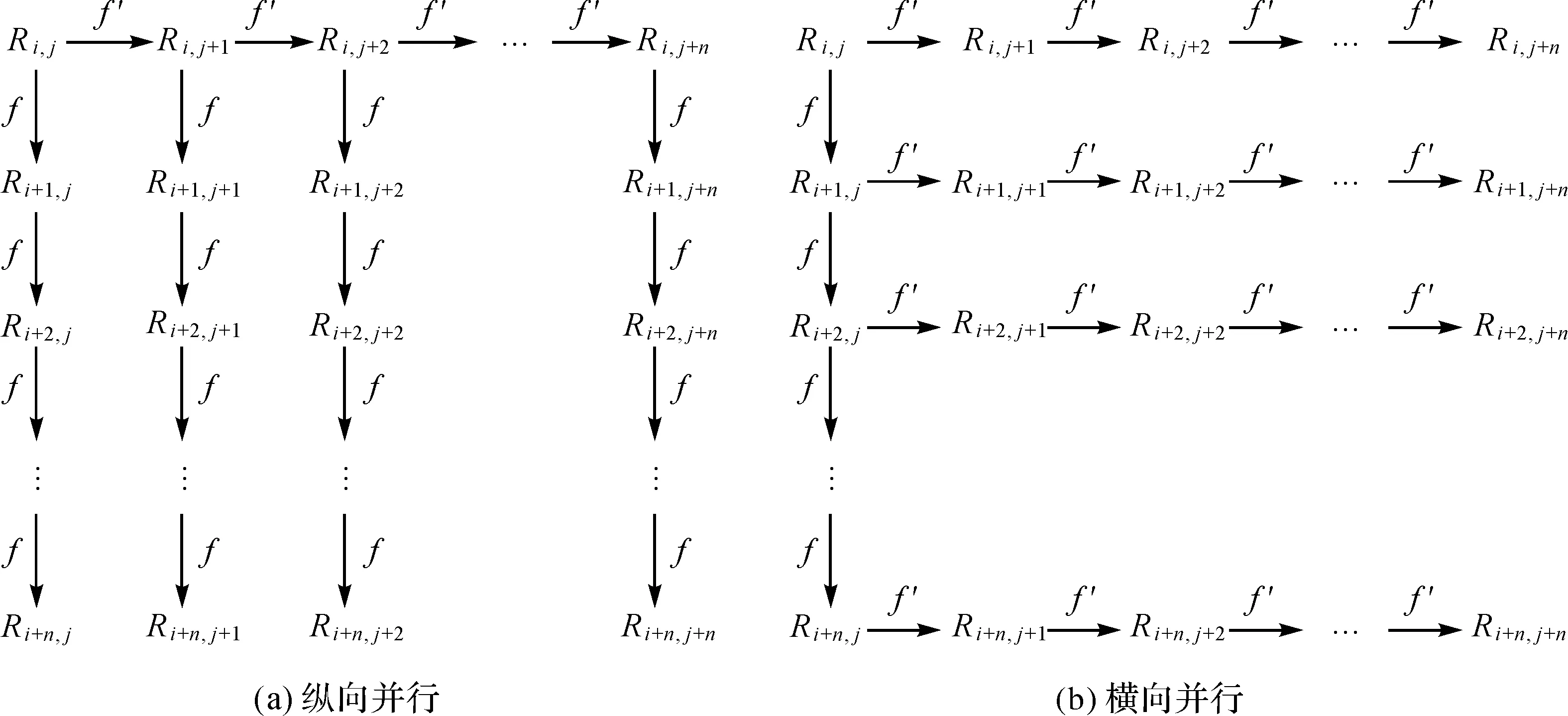
图2 一般性纵向并行与横向并行处理Fig.2 General longitudinal and horizontal parallel processing

经过推导[25]，采用式(1)对并行处理路径进行选择

(1)

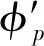
1.2 示例及讨论

(2)

即①划分的计算代价大于压缩时，采用横向并行(先划分再压缩)；②划分的计算代价小于压缩时，采用纵向并行(先压缩再划分)；③划分与压缩的计算代价近似时，为临界状态，采用横向并行和纵向并行均可。

(3)

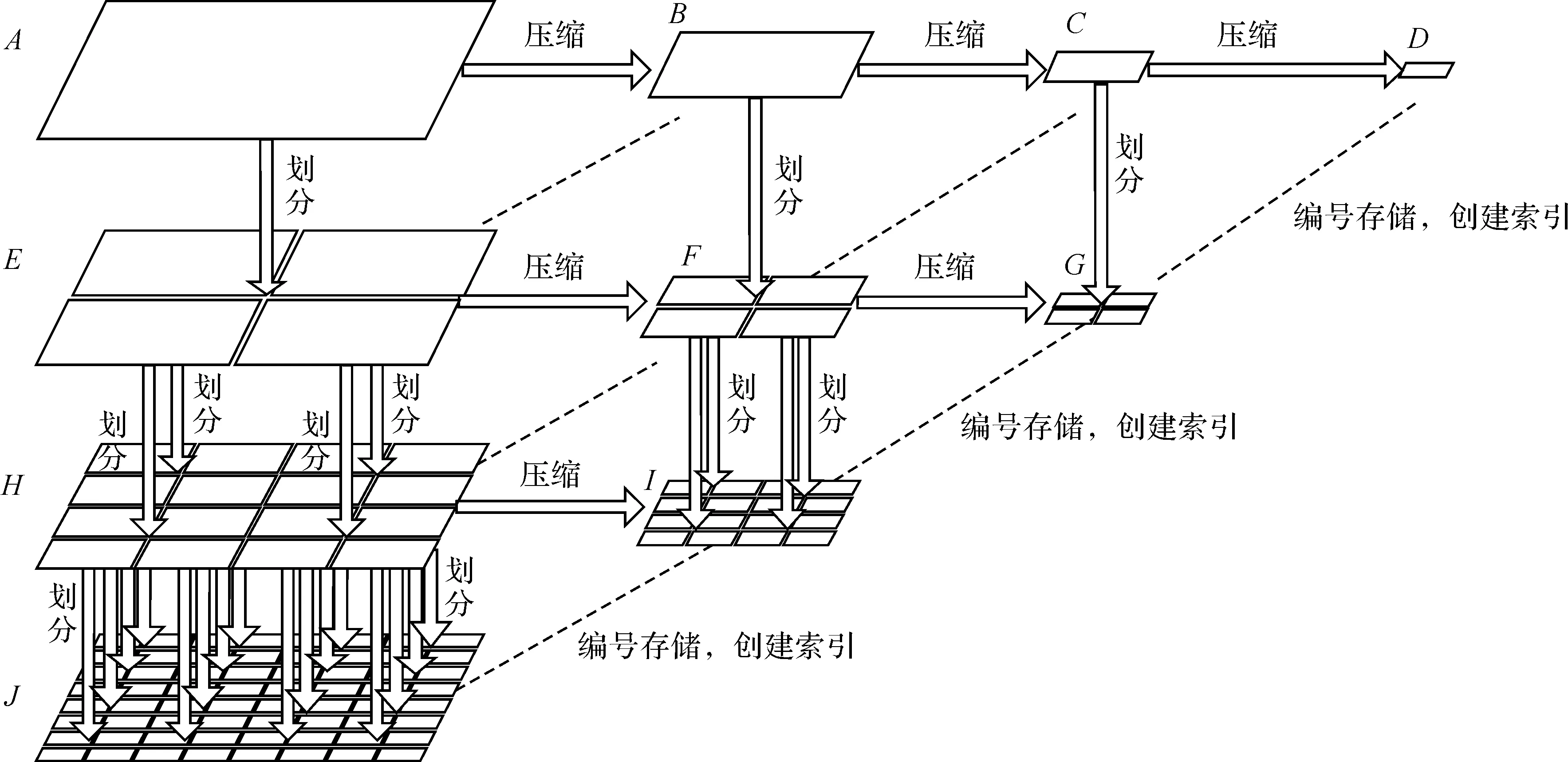
图3 生成四叉树索引(4层)Fig.3 Generating quadtree spatial index to image pyramid

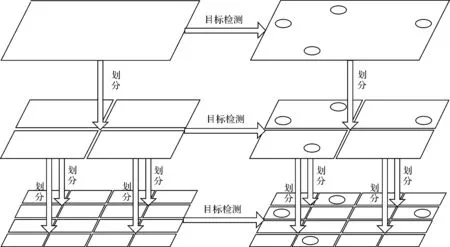
图4 栅格影像目标识别Fig.4 Detection and recognition parallel processing of target

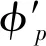
(3) 横向并行和纵向并行的多种并行操作组合(图5)。上述两个示例均为一个并行操作和划分操作组合的并行策略分析，本文提出的最佳并行策略可以推广到多个并行。例如，图5(a)给出了3个并行操作和划分操作，包含了两个纵向并行和一个横向并行组合，称为旋转门模型。旋转门模型是解决多个并行处理操作组合策略的问题，本质上是最优路径规划，而不是先后组合的问题。与“传统的、没有路径规划的”并行算法相比，旋转门模型的优势在于：可以实现在相同的遥感影像处理算法和同等的计算资源条件下，计算机自主选择最优处理路径，达到最优的遥感影像处理效率。旋转门模型以遥感影像数据划分为基础，是这个旋转门的主轴，每一扇门都是一个纵向或横向的选择(必定包含数据划分操作部分)，并且由于数据有多个冗余备份，每一扇门与其他扇门的操作都是可以同时进行的、独立并行的关系。如果不以划分为轴，这种组合起来的策略还可变成一个彼此为边的立方体模型(图5(b))。

此外，进一步讨论式(2)和式(3)可知，旋转门模型的路径判断准则可简单概括为“何种操作的单位计算代价大则先进行何种操作”。即，要获得全级别的栅格影像这一前提下，要实现多种并行处理操作组合的时间最优，则要优先进行计算代价大的操作。这一结论与传统的认知和经验不同，是旋转门模型的另一理论贡献。

2 算法实现流程描述及讨论

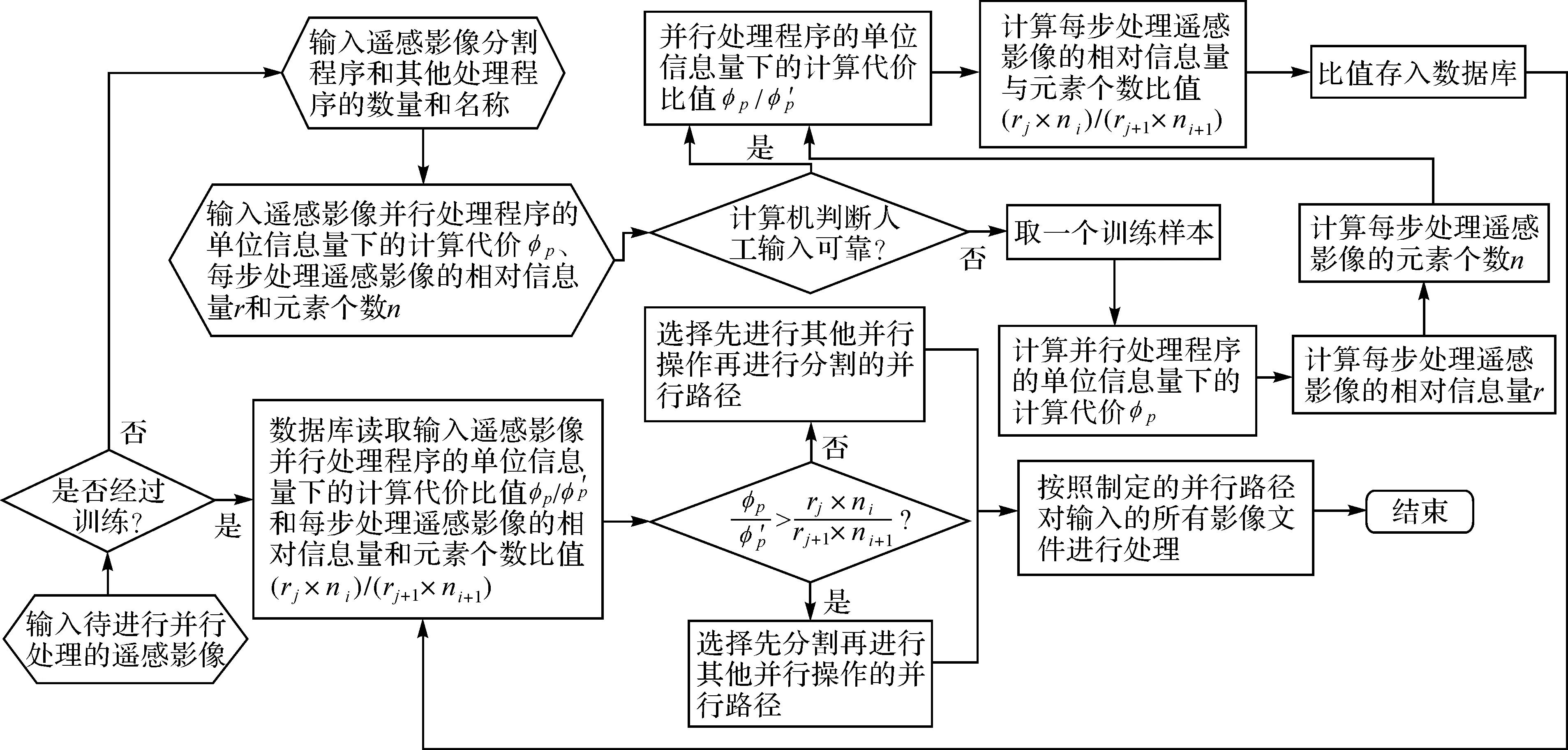
图6 算法流程Fig.6 Algorithm flow diagram

总之，通过实现算法的描述可知，旋转门模型原理简单实用，可以使计算机集群平台自动根据用户输入的遥感影像和指定的遥感影像处理程序准确地得到并行处理时间最短的最优路径，解决了将并行技术应用于海量遥感影像分布式存储和处理领域时其处理模型所具有的多路可达性所引起的路径动态、最优选择问题，满足了并行处理时耗时最短、最高效的要求。

特别的，在云计算或集群平台上，图2的纵向并行和横向并行的旋转门模型在计算节点上的实际运行过程示意图如图7所示。由图7可知，在实际运行过程中，除第1个计算节点之外，旋转门模型分配每个计算节点“非常有秩序地”都在做相同的操作，而且任何一个节点又都是一个不完全二叉树的子节点的根节点，它们遵守相同的规则，环环嵌套。这样的“秩序”是根据“计算时间最少”这一标准，由公式自动计算出来，没有人工干预。每个节点都做同样的操作对庞大的云计算平台有着诸多优势。例如，在同一个计算节点内，若指令快速缓冲存储区(cache)和数据cache都有限时，做同样的事情可以有机会让代码和数据一直在cache里，从而提高效率；再如，减少数据传输次数，规避数据传输瓶颈；还有，容错率高，不会影响其他计算节点的计算结果，容易找到出错节点或问题所在，容易恢复中断的处理和操作等等。综上，旋转门模型虽然是遥感影像处理领域的一个算法，但是从一个侧面反映了“秩序即效率”的自然或社会规律。

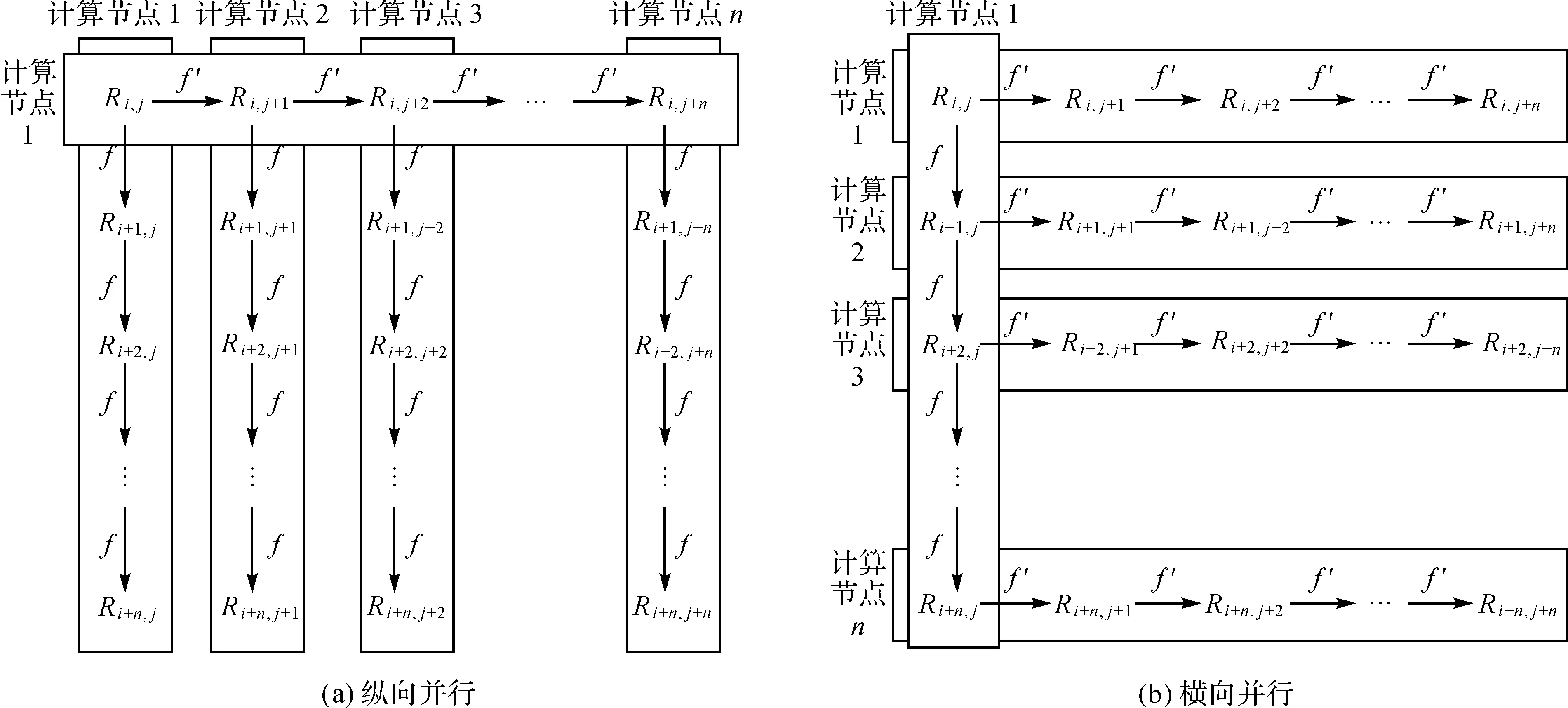
图7 纵向并行与横向并行的旋转门模型在计算节点上的实际运行过程Fig.7 Longitudinal and horizontal parallel processing on compute nodes

3 结果验证与分析

前文已经通过严密的理论论证提出了旋转门模型。旋转门模型的本质是多种并行处理的组合基础上的最优路径选择策略。前文在分析传统的遥感影像并行处理的缺点时，已经指出现有的并行处理策略只注重单一操作的并行处理，若完成数据划分、目标识别、数据压缩、投影变换、特征提取等处理过程，只能依次先完成数据划分再进行目标识别，然后数据压缩等。所以，第2节的理论模型就是在“多种遥感影像处理并行策略一定优于这些并行处理过程各自完成再串行”这一前提假设的基础上提出的。即旋转门模型与现有并行处理策略相比具有天然的优势。换句话说，旋转门模型可以实现在相同的遥感影像处理算法和同等的计算资源条件下，计算机自主选择最优处理路径，达到最优的遥感影像处理效率。所以本文试验的目的是为论证实际遥感影像并行处理过程中基于数据划分的最佳并行路径选择模型的正确性及其性能，并未重点测试比较旋转门模型与现有并行处理策略的高低(讨论部分间接说明了旋转门模型与现有并行处理策略的优势)。试验内容以四叉树金字塔并行生成过程和目标识别为例，测试了“先压缩再划分和先划分再压缩”、“先识别再划分和先划分再识别”的运行时间，最后结合压缩算法、目标识别算法和划分算法的计算代价，对上述两个测试结果进行深入分析。需要说明的是，数据量和软硬件环境不同会影响测试时间，但是最优路径的选择结果和结论不会发生变化。

3.1 测试环境

测试采用名字节点3个，配置为表1中第1及第2类共3台PC机；计算节点32个，配置为表1中8类共32台PC机。本文试验的软件环境简单，Windows操作系统运行稳定、操作方便、安全性较高，为保证系统的正常运行，服务器端操作系统采用Windows 2008 Server(64 bits)或Windows 2003 Server(32 bits)。其中，选择Windows 2008 Server是为运行Dryad平台，选择Windows 2003 Server(32 bits)是用其作为UDDI的服务目录服务器。对客户端理论上没有要求，任何安装了网络浏览器的普通PC机均可作为客户端。

数据选择表2所示数据，其数据量从200 MB到5.58 GB不等。

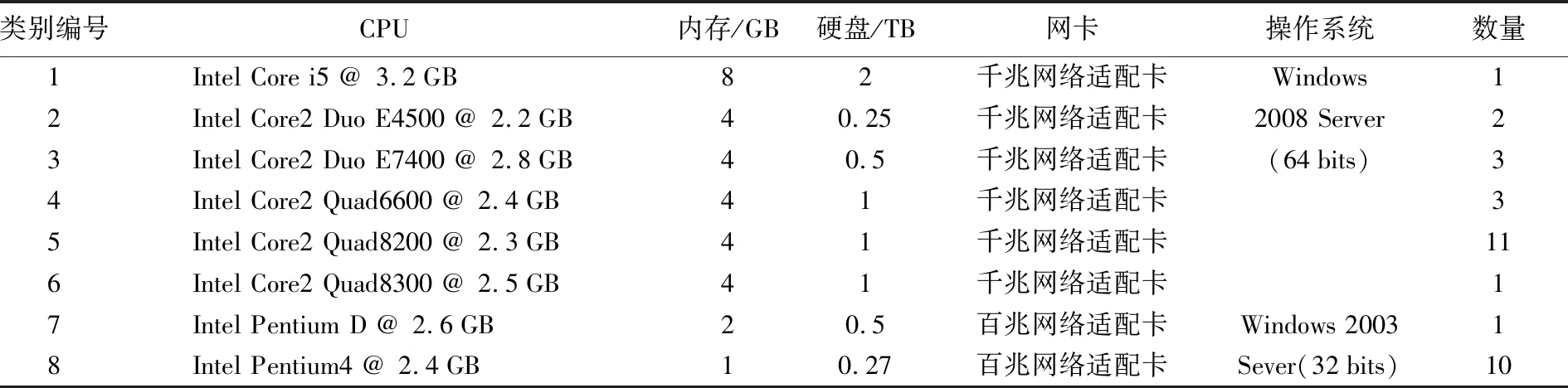
表1 PC机及网络设备配置

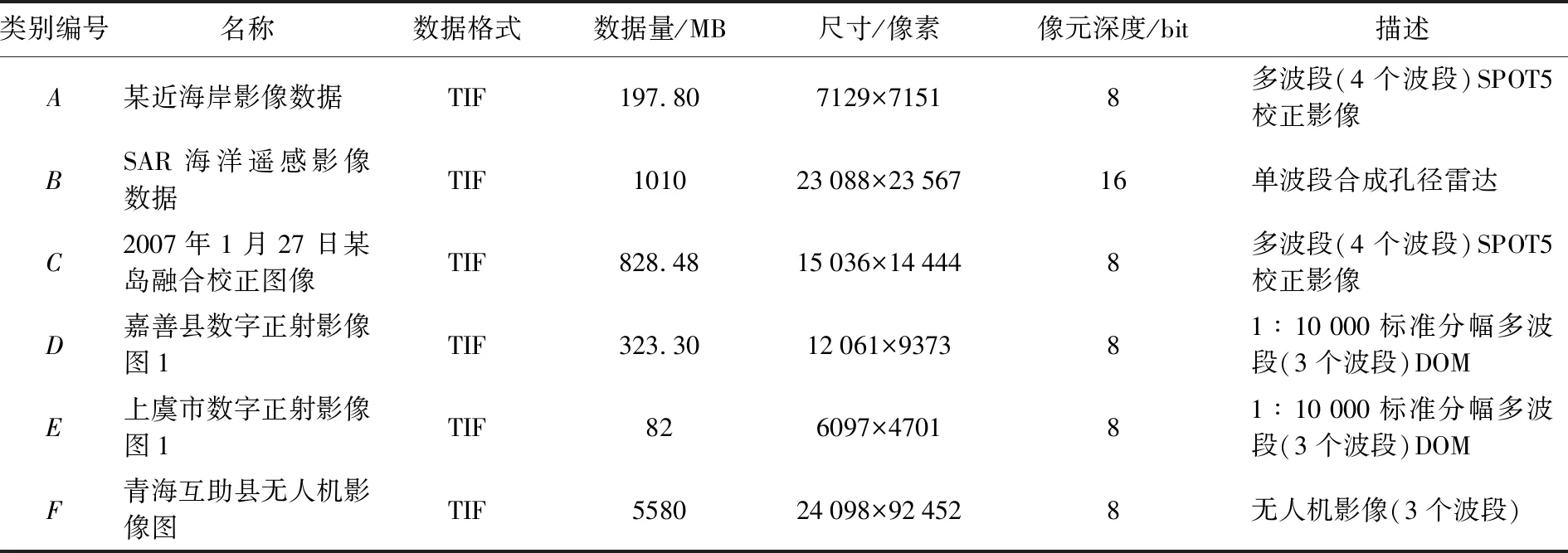
表2 试验用栅格数据

3.2 测试内容

3.2.1 生成四叉树金字塔(压缩和划分组合策略测试)

测试1：使用10个计算节点，对测试数据A采用先压缩再划分的并行策略，构建8、10、12层四叉树金字塔，记录总时间；使用10个计算节点，对测试数据A采用先划分再压缩的并行策略，同样构建8、10、12层四叉树金字塔，记录总时间。

测试2：测定压缩和划分操作的单位信息量下的计算代价φp。分别请求压缩和划分操作，则云端的计算节点分别使用ENVI/IDL算法执行压缩(将一份影像数据按四叉树金字塔的压缩方法进行压缩)和划分(将同一份影像数据划分64份)处理，分别记录栅格数据A—F压缩和划分时间，并计算出相同环境下单位信息量下的计算代价。

3.2.2 目标识别(目标识别和划分组合策略测试)

测试1：本文采用Tensorflow与CNN卷积神经网络结合的目标识别方法*，使用10个计算节点，对测试数据F采用先目标识别再划分的并行策略，构建2、3、4层数据，最终将4、16、64份数据均匀存储在计算节点上为止，记录1—2级、2—3级、3—4级的时间；使用10个计算节点，对测试数据F采用先划分再目标识别的并行策略，同样构建2、3、4层数据，最终将4、16、64份数据均匀存储在计算节点上为止，记录1—2级、2—3级、3—4级的时间。

测试2：测定目标识别和划分操作的单位信息量下的计算代价φp。分别请求目标识别和划分操作，则云端的计算节点分别使用ENVI/IDL算法执行目标识别(将一份影像数据按Tensorflow与CNN卷积神经网络结合的目标识别方法进行目标识别)和划分(将同一份影像数据划分64份)处理，分别记录栅格数据A—F目标识别和划分时间，并计算出相同环境下单位信息量下的计算代价。

为了客观起见，本测试试验运行50～100次，取其均值作为试验结果。表3和表5结果为实际并行处理过程模拟，故包含传输时间。

3.3 测试结果

3.3.1 生成四叉树金字塔(压缩和划分组合策略测试)

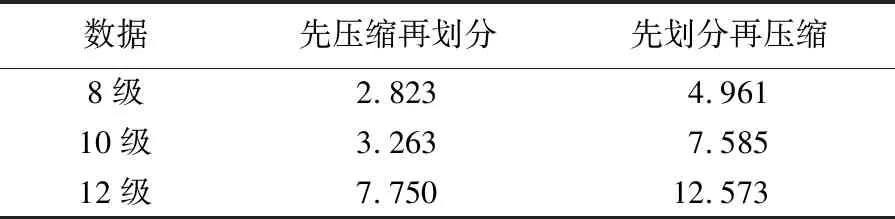
栅格数据A采用不同的并行策略获得的测试结果如表3所示。

表3 栅格数据A构建四叉树金字塔并行策略测试结果

Tab.3 Results of building quadtree pyramid parallel processing of dataAmin

测定压缩和划分操作的单位信息量下的计算代价如表4所示。

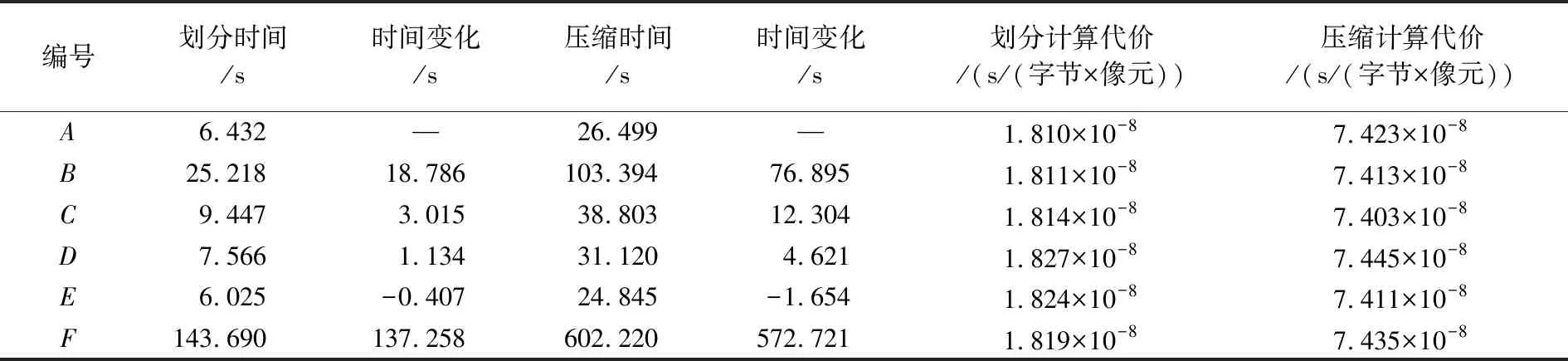
表4 单位信息量下的计算代价测定结果

3.3.2 目标识别(目标识别与划分组合策略测试)

栅格数据F采用不同的并行策略获得的测试结果如表5所示。

测定目标识别和划分操作的单位信息量下的计算代价如表6所示。

表5 栅格数据F目标识别并行策略测试结果

Tab.5 Results of target detection and recognition parallel processing of dataFh

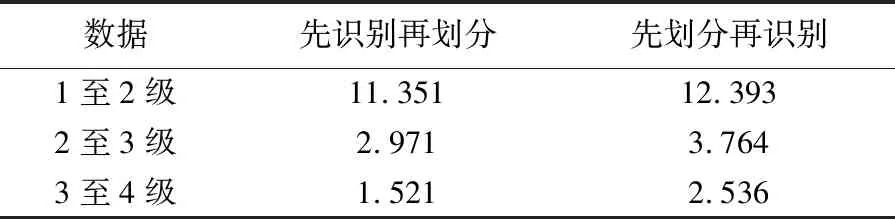
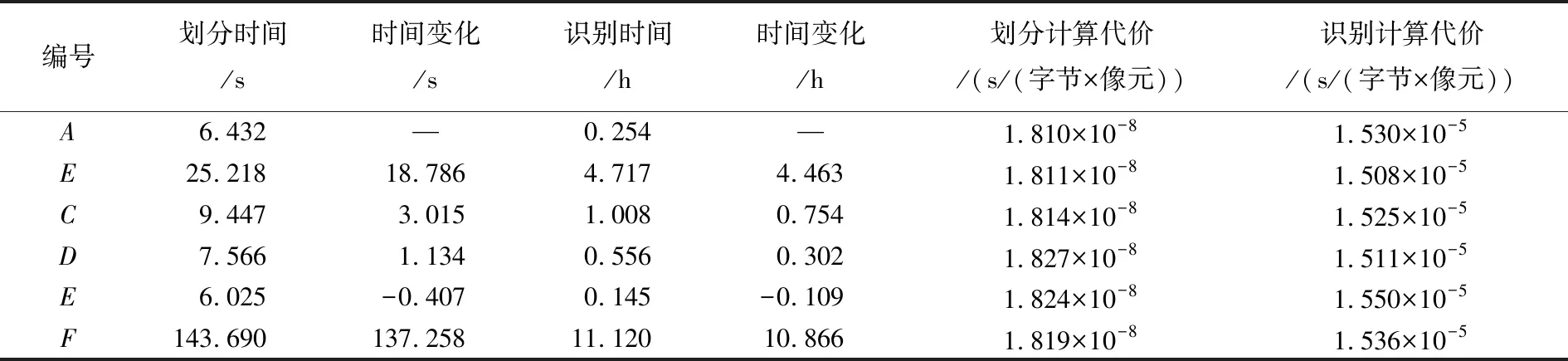
表6 单位信息量下的计算代价测定结果

3.4 结果讨论

3.4.1 生成四叉树金字塔(压缩和划分组合策略测试)

由图3可知，若创建n级金字塔索引，则该索引中的文件总数Sn为

(4)

那么，栅格数据A在构建8级、10级、12级金字塔索引过程中新生成29 123份、466 029份、7 456 535份图像文件。同理，若原始图像的数据量为a，则数据总量m为

(5)

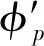
3.4.2 目标识别(目标识别和划分组合策略测试)

目标识别是一个数据量增加的过程，易从表5结果获知“先识别再划分”的并行策略远远优于“先划分再识别”的并行策略。从表6可知，目标识别的单位信息量下的计算代价远远大于划分，所以进行先识别再划分的策略是正确的。“先划分再识别”的策略(横向并行)，相对“先识别再划分”策略会让计算节点过多地处理复杂的识别处理操作，从而会降低整体的计算效率。此外，从表6可知，由于目标识别算法的单位计算代价过大，且与数据量和像元数量正相关，所以传统方法中，将原数据分割成几份再进行并行目标识别会减少数据处理的总时间。但是，旋转门模型却告诉我们，在生成全级别的栅格影像并同时实现目标识别操作时，要“先识别再划分”，然后再将各级别的结果分布存储于云计算平台上，既能保证数据完整性和目标识别的准确性，又能保证效率最高。

3.4.3 目标识别、数据压缩和数据划分综合并行操作组合

综上，若同时进行目标识别、数据压缩和数据划分综合并行组合操作，生成全级别的栅格影像时，最优路径应是“目标识别—数据压缩—数据划分”或“目标识别—数据划分”与“数据压缩—数据划分”两种选择，此路径即能保证时间效率最高，又能保证数据操作的正确性。若先进行数据压缩或数据划分操作，则目标识别则需要重新训练样本，除时间效率低下之外，还会增加多余的操作时间。

4 结 论

得益于云计算理论和技术的提出，遥感影像的处理可以实现对同一份数据进行多任务的并行处理。本文在此前提下，深入研究了基于数据划分的遥感影像并行处理问题，提出了8个定义(数据态、信息量、元素、映射过程、表达式、并行维数、计算代价与纵向/横向并行)，6个性质(有向性、传递性、繁殖性、多维性、同一性与多路可达性)。以这些定义和性质为基础，从相邻数据态之间的一次映射逐步推导致“基于数据划分的遥感影像并行处理”的一般情况，提出最佳并行路径选择模型——旋转门模型，用于解决将并行技术应用于遥感影像分布式存储和处理领域时，其处理模型所具有的多路可达性所引起的路径动态、最优选择问题。本文的贡献在于：在批量处理海量遥感数据的情形下，同时实现遥感数据生成、目标识别等并行任务时，最优并行路径的选择只与平均计算和数据态的相对信息量、元素个数的比值这一标志有关，而且从原始数据(源数据态1)到最终数据(最终数据态n)的诸多并行路径中，看似复杂，其实只有独立上行和独立下行组成的单向最优路径。

本文还进一步给出四叉树索引并行生成、基于四叉树的目标识别并行处理的研究结果。指出在四叉树索引并行生成过程中，如果划分的计算代价大于压缩时，采用先划分再压缩的横向并行；如果划分的计算代价小于压缩时，采用先压缩再划分的纵向并行。基于四叉树的目标识别并行处理操作中，当检测结果很多时，无论划分映射过程和目标识别映射过程的效率如何，采用纵向并行(先目标识别再划分)的策略才能实现最优化并行。

本文提出了基于数据划分的遥感影像并行处理问题的基本概念和性质，最终立足于最佳并行路径选择问题上。在模型的提出上，使用了简单直观的遥感影像二维矩阵来抽象表示遥感数据(可以理解为TIFF格式)，并在此基础上提出概念、性质和公式推导，最后得出结论。实际上，遥感数据在云计算平台中存储方式多样，如果把一个二维矩阵按行重新组织成一维直线(1个像元高度)。原本二维矩阵里读取一行或一列都很方便，现在，在一维直线中读取一行可以直接根据偏移量连续读取，但是如果读一列需要先算好起始点和长度，然后每隔固定像元读取一个像元，这种情况下就无法批量读取；同样如果将二维矩阵按列重新组织成一维直线，则按行批量读取时也会有问题。得益于云计算环境中同一份数据的多个冗余备份特性，在实际应用中，将遥感影像既按行存储也按列存储，并设计调度器对不同的遥感影像处理程序进行调度，依据需要来处理按行存储或按列存储的一维数据。所以，实际存储方式并不影响本文提出的算法模型及相关理论。只是基于不同的遥感数据存储结构或存储方式，需要对模型进行具体化。同时针对不同的遥感影像处理方法，也需要对模型进行具体化，还要考虑很多算法在实际应用时的细节，特别是容错性和健壮性问题，这些都将是未来的研究工作的重点。此外，基于本文提出的概念和性质，遥感影像并行处理问题还有很多其他的内容可以研究，例如，负载均衡、质量检验等，而这些将在未来的研究工作中深入展开。