顾及几何特征相似性的多源等高线匹配方法
2019-06-10郭文月刘海砚余岸竹丁梓越
郭文月,刘海砚,孙 群,余岸竹,丁梓越
信息工程大学,河南 郑州 450052
等高线匹配是地形图局部更新与融合的重要环节,其匹配效率与准确度很大程度上影响空间数据更新与融合质量[1]。等高线匹配同时也可以应用于导航定位[2]、空间聚类[3]、变化检测[4]以及地形要素与地物要素的制图综合[5]等领域。多源数据中同类要素对象间的匹配关系需要通过几何特征、属性特征及拓扑关系的相似性比较来建立[5],目前相关领域的研究大多基于等高线空间拓扑关系构建及相似性度量等方法。
基于等高线空间拓扑关系构建的等高线匹配与融合方法首先依一定规则建立某种树结构,通过对无序等高线集群有序化、组织化和结构化,表达等高线的空间位置信息及等高线之间隐含的空间邻近关系[6-10],进而根据等高线树所表达的位置信息和关系信息辅助实现不同来源等高线数据之间的同名等高线融合与匹配。同时,为了适应地形图局部更新过程中区域边界处出现大量非闭合等高线的情况,文献[8]提出了顾及地形特征的等高线空间关系表达方式,优化等高线树构建;文献[9]提出基于约束Delaunay三角网的等高线层次结构构建方法,一定程度上克服了等高线被图幅截断的问题,但对于一些特殊地形如陡坎、悬崖等,生成等高线树存在困难;文献[11]提出利用分区二叉树、增量等高线束和拓扑关系网来组织包含未闭合等高线间的拓扑关系;文献[12]基于线—线拓扑关系制定了多源等高线间的融合与更新规则。但当地形变化剧烈或在拓扑关系复杂区域,基于拓扑关系的同名等高线融合与匹配的正确率和自动化处理能力会受到一定影响[12]。
基于相似性度量的匹配与融合方法认为曲线间的空间关系和邻近程度更能反映其相似性。文献[13]提出了线群目标间顾及空间关系和几何特征的相似性度量模型,但该模型在应用于等高线匹配时易受局部变形较大点的影响;文献[14]提出了计算两条曲线之间离散Fréchet距离的方法,利用线状要素节点之间的欧氏距离度量有序点集之间的距离,进而描述线状要素的相似程度,更加适用于等高线匹配;文献[15—17]基于该方法研究了不同比例尺地图数据线状要素匹配;文献[18]提出了基于最短路径的平均Fréchet距离和“部分—整体”Fréchet距离计算方法,减少匹配误差,解决了部分与整体匹配问题并将其应用于等高线内插。但当线状要素局部变形较大时,这种用节点之间的欧氏距离衡量线状要素之间相似程度的度量方法可能存在较大误差。另外,此类基于空间欧氏距离的方法更加侧重体现线状要素在空间位置上的相近性,而没有能够衡量其在几何形态上的相似性,在等高线分布密集区域,当匹配候选集内存在多条干扰等高线时可能会出现误匹配的情况。
针对上述问题,本文提出一种顾及几何特征相似性的等高线匹配策略,采用节点曲率以及法向量与横坐标轴夹角(curvature and the angle of normal vector,CANV)作为混合特征描述测度,提取等高线几何形态特征,将等高线节点序列转化为空间几何形态特征描述序列,并引入最长公共子序列算法(longest common subsequence solution,LCSS),量化计算多源等高线之间在几何形态上的相似和差异程度,实现同名等高线匹配,并利用模拟数据和真实数据进行试验验证。试验结果证明本文提出的基于几何特征相似性的等高线匹配策略具有较高匹配精度和运行效率,并具有较好的适用范围,实现了融合位置特性和几何形态特性的等高线匹配,为局部地形数据更新提供依据。
1 特征提取与相似性度量
1.1 等高线匹配策略
顾及几何特征的匹配过程一般包含形态特征提取和形态特征匹配[19]。基于这一认识,本文设计了顾及几何特征相似的等高线匹配策略,先根据空间位置相近和高程值相等的原则进行粗匹配,再通过特征序列转化和相似度计算的推进式过程,实现同名等高线精匹配,旨在提高多源等高线匹配的匹配精度。具体实施流程如图1所示,主要分为粗匹配和精匹配两个部分。
在粗匹配过程中,首先读取不同来源的原始等高线集和待匹配等高线集,然后构建原始数据集中等高线的缓冲区,在与原始等高线缓冲区相交的待匹配等高线集内按照高程值相等的原则进行等高线粗匹配。为避免相邻等高线缓冲区之间过度重叠,导致候选等高线集过大,缓冲区半径应小于相邻等高线之间的实际水平距离,但由于等高线各处坡度可能存在差异,因此可用相邻等高线点集之间的平均距离替代等高线间的实际水平距离[20],或根据区域内等高距以及不同地形对应的坡度范围合理设置缓冲区半径。对于存在多条待匹配等高线的情况,需要根据粗匹配结果生成精匹配候选集,再进一步实施精匹配。以图2中等高线为例,经粗匹配后,与原始等高线A缓冲区相交的等高线集{B1,B2}构成A的精匹配候选集。由于等高线B1、B2高程值均与原始等高线A相等,且B1、B2为并列等高线,仅依据拓扑关系难以判断B1、B2是否均为A的同名等高线,因此需进一步对精匹配候选集内的等高线实施精匹配。
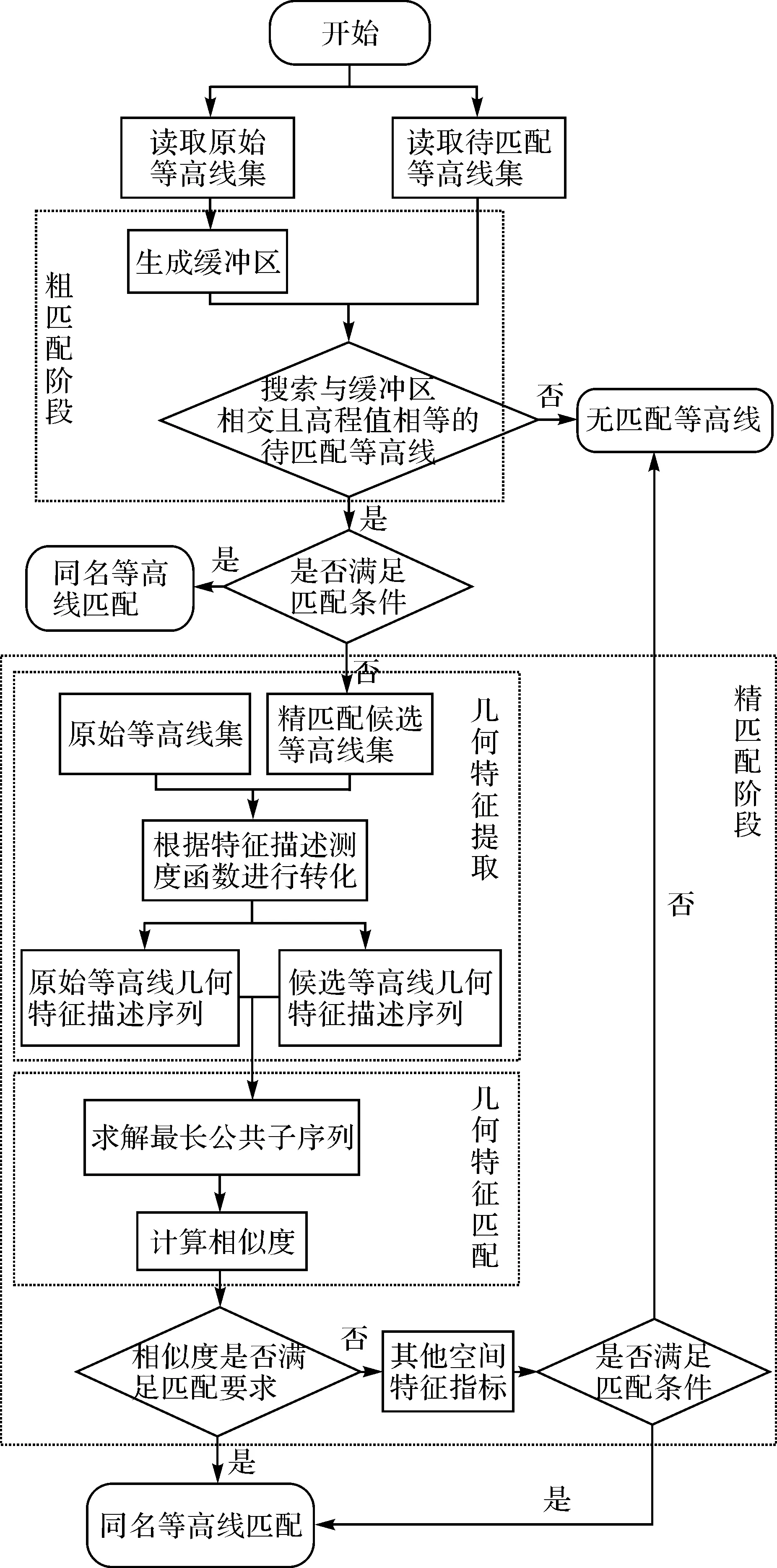
图1 顾及几何特征相似性的等高线匹配策略Fig.1 The contour matching strategy considering the similarity of geometric characteristic
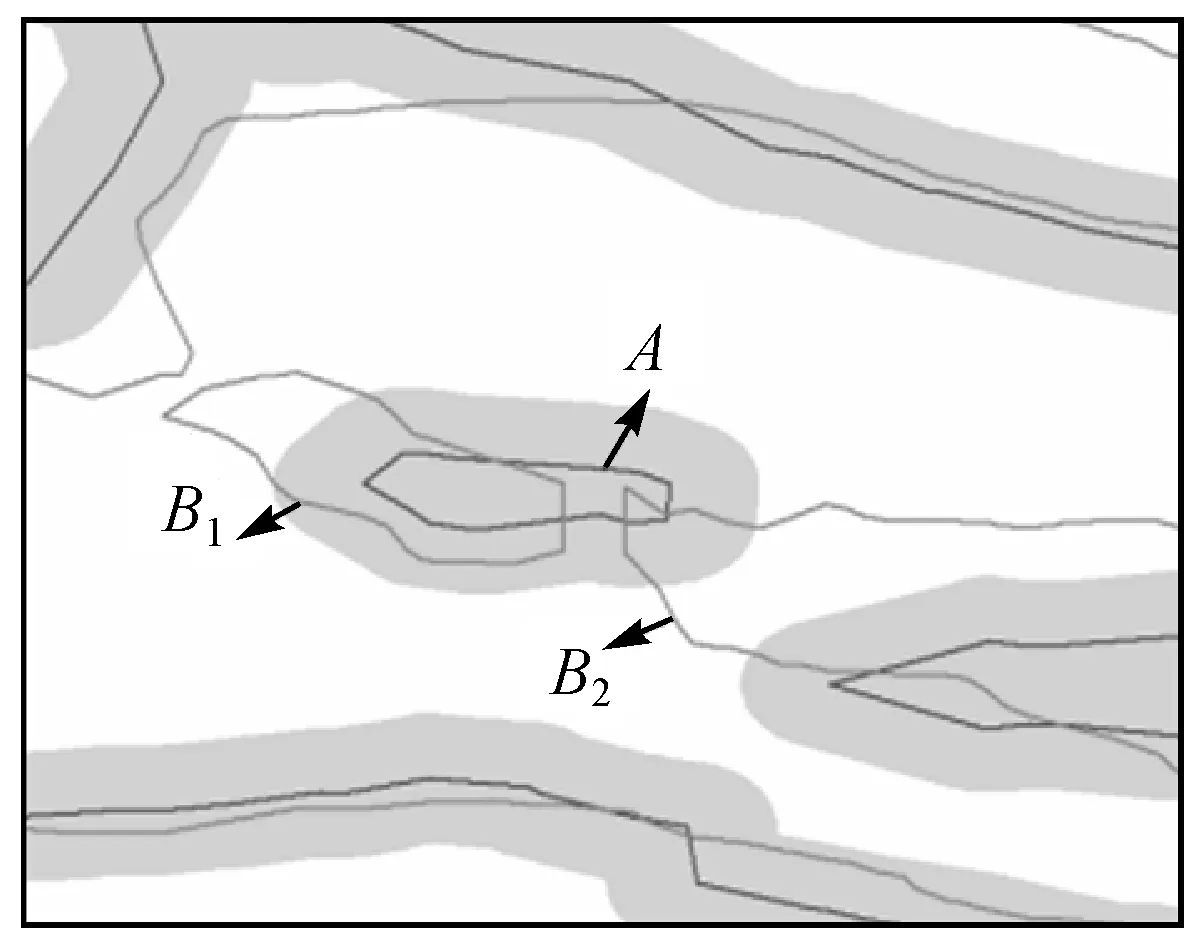
(此图中相关要素及数值为虚构)图2 基于空间邻近和高程值相等原则粗匹配Fig.2 Coarse matching based on spatial adjacency and elevation
在精匹配阶段,本文提出先利用特征描述测度函数提取等高线几何形态特征,将等高线的二维节点序列转化为几何形态特征描述序列,将等高线匹配问题转化为特征描述序列匹配问题,再引入最长公共子序列算法求解特征描述序列间的最长公共子序列,进而计算原始等高线与其精匹配集内候选等高线之间的相似度,根据相似度值的大小确定同名等高线,如仍存在无法确定的情况,则需结合曲线长度、曲折系数等其他空间特征信息进行辅助判断,最终实现同名等高线匹配。
基于上述匹配策略,特征描述序列转化、最长公共子序列求解及相似度计算是顾及几何特征相似性的等高线匹配策略中的关键环节。为了克服单一特征测度函数在描述等高线几何形态特征时的局限性,本文提出一种顾及曲线一阶变化率和二阶变化率的混合特征描述测度,通过增加控制参数的方式优化特征描述序列的最长公共子序列求解过程,并提出以最长公共子序列长度来量化衡量多源等高线之间相似程度的方法。
1.2 特征描述序列转化
设两条不同来源等高线A、B包含的二维节点个数分别为n和m,则可分别表示为A=((ax,1,ay,1),(ax,2,ay,2),…,(ax,n,ay,n)),B=((bx,1,by,1),(bx,2,by,2),…,(bx,m,by,m))。首先需要将等高线二维节点序列通过映射转化为表征其几何形态特征的一维特征描述序列A′、B′,本文利用特征描述测度函数实现几何形态特征提取。
定义1:特征描述测度函数f。定义特征描述测度函数f将等高线上二维节点序列映射为一维几何特征描述序列,即f:(ax,i,ay,i)→ai,f:(bx,j,by,j)→bj,如图3所示。
一维特征描述序列应该反映原始节点序列的主要几何形态特性,测度函数应选择能够反映等高线几何形态特征的函数[21],对几何形态描述越准确详尽,其匹配结果越准确。在构建特征描述测度函数的过程中,基于曲率[22]、凹凸形态[23]以及弦长[24]的测度函数在形状识别与检索过程中均具有较好的效果,但单一描述测度难以满足复杂形状描述需求[25]。为了保证对原始等高线几何形态描述的准确性和稳定性,同时保证运算效率,本文提出一种基于节点曲率以及法向量与横坐标轴夹角(curvature and the angle of normal vector,CANV)的混合特征描述测度。
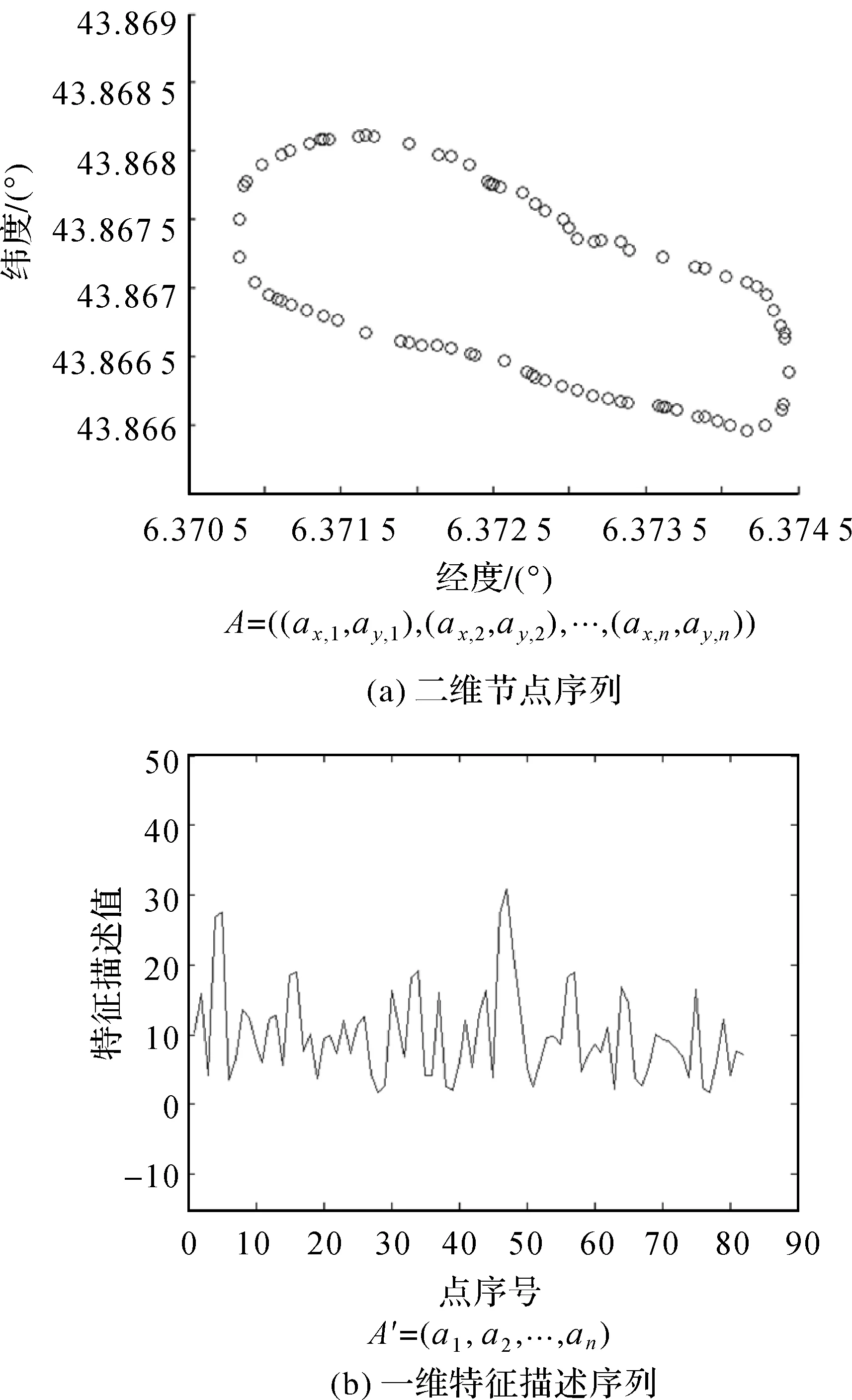
图3 二维点序列与一维特征描述序列Fig.3 The two-dimensional point sequence and the one-dimensional feature descriptive sequence
曲率是几何学中对几何体不平坦程度的一种衡量指标,等高线节点处的曲率反映了该点曲线弯曲程度。由于节点处的一阶和二阶导数可由数值微分近似计算,因此节点(ax,i,ay,i)处曲率测度函数可表达为
(1)
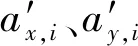
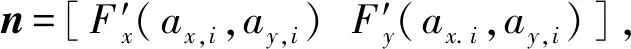
(2)
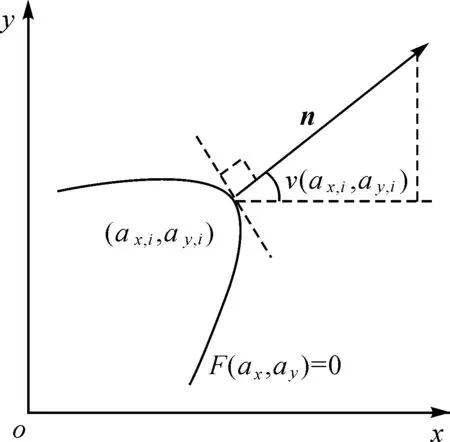
图4 节点法向量与横坐标轴夹角Fig.4 The angle between normal vector and x-axis
曲率和法向量夹角分别从二阶变化率和一阶变化率刻画曲线的局部几何形态特征。基于此,在对等高线节点序列进行特征描述转化时,选取曲率以及法向量与横坐标轴夹角作为混合特征描述测度。为避免经两种测度转化后的特征描述值在数值上差异过大,需进行归一化处理
(3)
(4)
式中,minρ、minv分别为曲率测度和法向量夹角测度序列中的最小值;maxρ、maxv分别为曲率测度和法向量夹角测度序列中的最大值。在特征描述转化过程中,设曲率测度的权值为λ,则法向量夹角测度的权值为1-λ,据此得到等高线匹配的混合测度(CANV)函数表达公式
f(ax,i,ay,i)=λρ′(ax,i,ay,i)+(1-λ)·
v′(ax,i,ay,i)
(5)
基于CANV测度函数,等高线节点序列A的特征描述序列为A′=(a1,a2,…,an),节点序列B的特征描述序列同样可通过上述转化函数获得,可表示为B′=(b1,b2,…,bm)。至此,等高线的二维节点序列均已转化为一维特征描述序列。
1.3 最长公共子序列求解及相似性度量
两个序列X(x1,x2,…,xn)、Y(y1,y2,…,ym)的所有公共子序列中,长度最长的即为X和Y的最长公共子序列(longest common subsequence,LCS)。由于其能够量化表现不同序列之间的相似程度,被广泛应用于版本控制、文件匹配和重复率检测等领域[26-28]。基于上文对等高线数据进行的特征描述序列转化,同名等高线匹配问题转化为等高线特征描述序列间的最长公共子序列求解问题。
常用的最长公共序列问题求解方法为动态规划法,对于长度分别为n、m的序列X、Y,其最长公共序列求解方法可表达为
(6)
在多源等高线匹配过程中,原始等高线与待匹配等高线之间的对应点集组成其公共子序列。然而由于不同来源的等高线数据所包含的节点个数以及节点在曲线序列中的位置存在差异,序列间的对应点并不是严格的数值相等关系,在解算过程中需要给定控制参数来优化和控制解算过程。
定义2:控制参数δ和ε。设定一个整数δ,用于控制节点的搜索宽度,在节点序号相差δ范围内搜索对应点;设定阈值实数ε,0<ε<1,对应点间的特征描述值差值应在阈值范围内。控制参数值应结合等高线包含的节点个数且保证运算效率的同时在一定范围内合理取值。本文试验中δ按两条待匹配等高线包含节点个数较少值的一定比例取整,ε取两条等高线特征描述序列标准差的较小值。
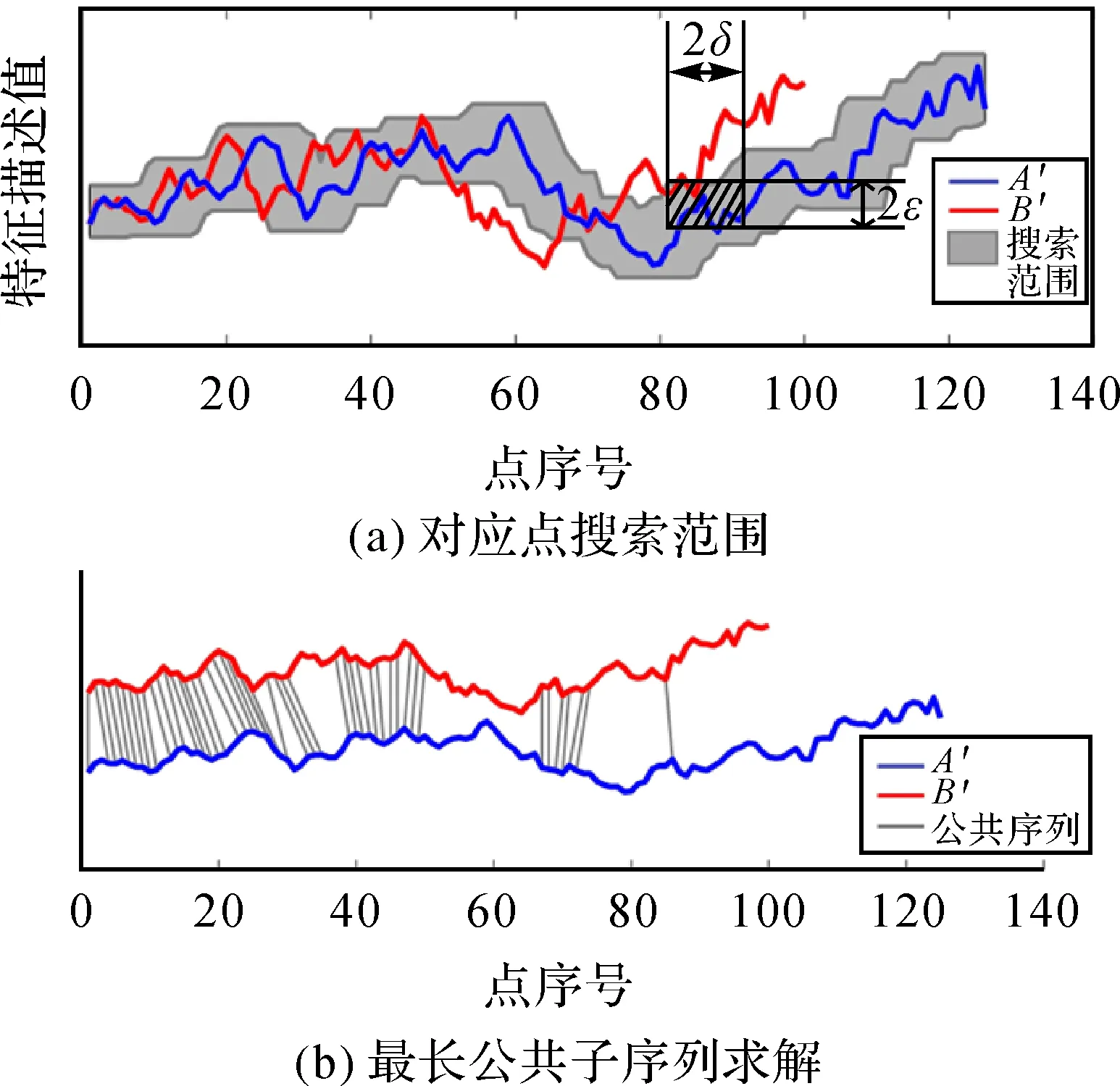
如图5(a)所示,参数δ和ε控制了在等高线特征序列A′、B′中求解对应点时的范围,图5(b)表示两个特征描述序列间的对应关系,即最长公共子序列的解算结果,则基于控制参数的最长公共子序列解LCSSδ,ε(A′,B′)表达为
LCSSδ,ε(A′,B′)=
(7)
式中,head(A′)=(a1,a2,…,an-1);head(B′)=(b1,b2,…,bm-1)。
基于上述特征描述测度函数f和求解控制参数δ、ε,多源等高线A、B的特征描述序列之间基于控制参数的最长公共子序列求解算法实现为:
a←f(A)
b←f(B)
n←length(a)
m←length(b)
fori1 ton
LCSS[i,0]←0
fori1 tom
LCSS[0,i]←0
fori1 ton
do forj←i-δtoi+δ
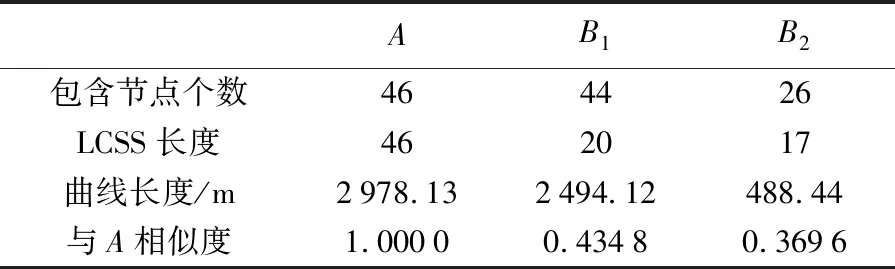
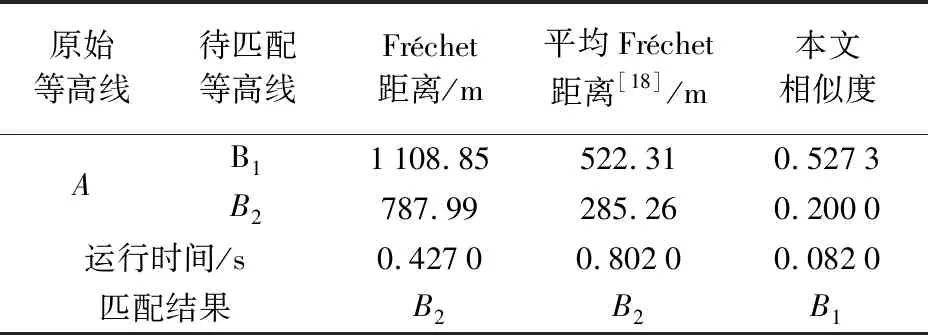
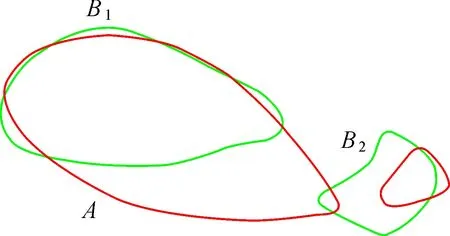
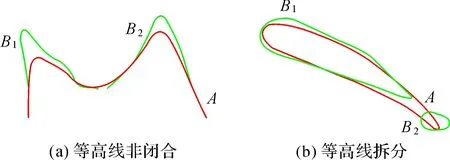
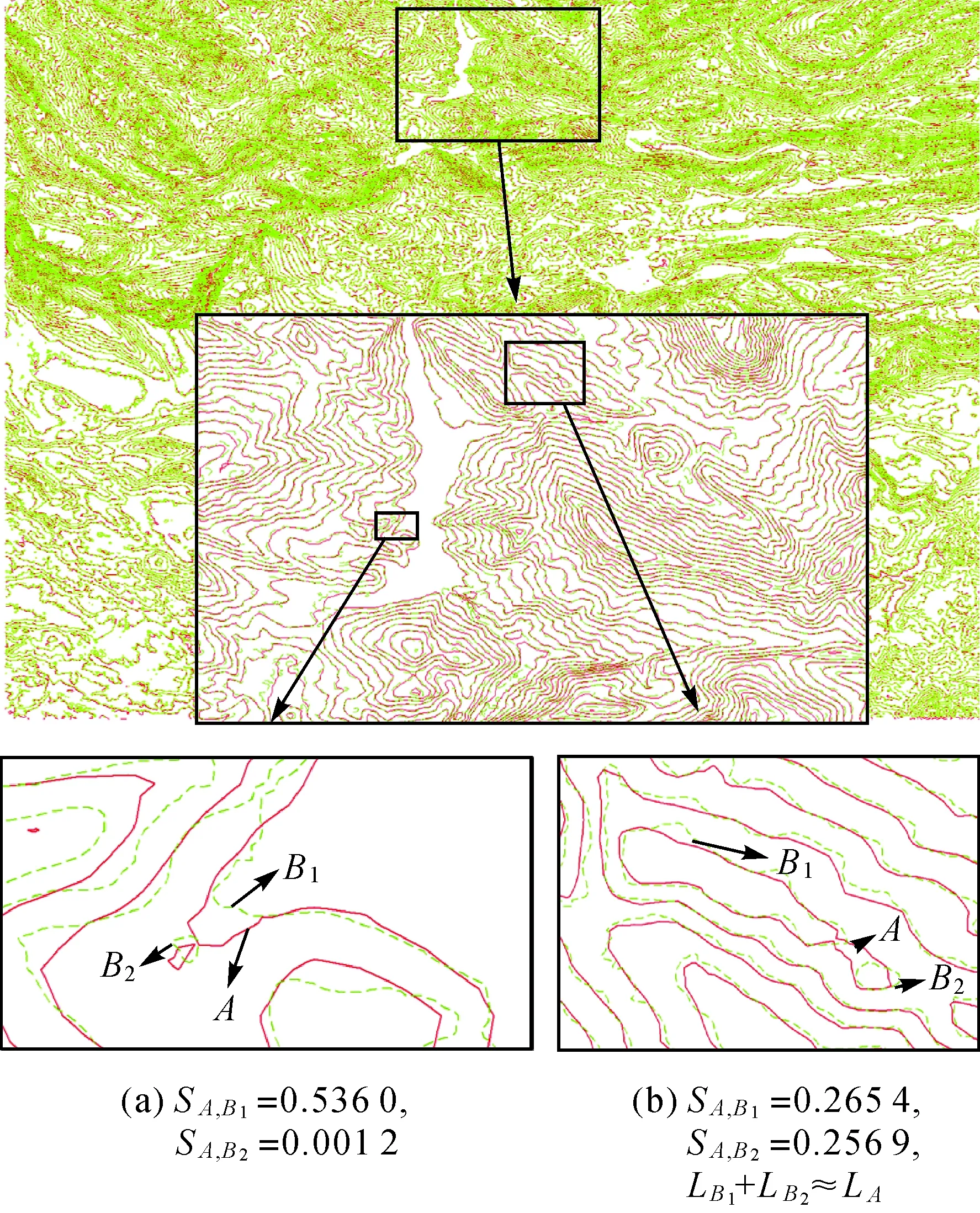
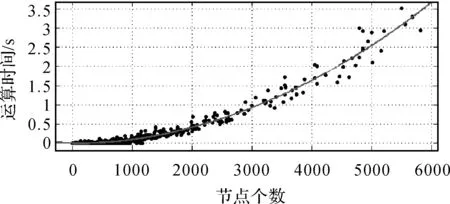
ifj>0 andj ifb[j]+ε≥a[i] andb[j]-ε≤a[i] LCSS[i,j]←LCSS[i-1,j-1]+1 else if LCSS[i-1,j]>LCSS[i,j-1] LCSS[i,j]←LCSS[i-1,j] else LCSS[i,j]←LCSS[i,j-1] return LCSS 定义3:相似度S。参照文献[26]和文献[28]中的策略,基于控制参数δ和ε,将包含节点个数分别为n、m的多源等高线A、B之间的相似度S定义为 (8) 式中,A′、B′分别为A、B的特征描述序列。由式(8)易知,S∈[0,1],相似度值随等高线之间的几何形态相似程度增加而趋近于1,当两条等高线的空间位置、几何形态以及包含节点数完全一致时,S=1。在原始等高线的匹配候选集内,认为相似度值较大的待匹配等高线为其同名等高线,在相同匹配范围和数据集条件下,同名等高线间相似度越小,说明该区域地形变化越明显。 分别利用模拟试验和真实数据试验对本文提出的混合特征描述测度(CANV)和顾及几何特征相似性的等高线匹配策略的适用性、匹配精度及运行效率进行验证。 在模拟试验部分,针对已有方法在等高线匹配过程中可能出现的不适用情况,对本文提出的混合测度(CANV)及匹配方法的有效性进行验证: (1) 模拟试验1用于验证本文提出的混合特征描述测度(CANV)在等高线相似性量化度量中的可靠性。 (2) 模拟试验2用于验证在解决非闭合等高线及地形变化引起的一对多匹配问题时本文方法的适用性。 (3) 模拟试验3用于验证在已有的基于欧氏距离相似性度量方法可能导致误匹配的情况下,本文方法的有效性。 在真实数据试验部分,利用法国某地的DEM数据所生成的等高线对本文方法的匹配精度和运行效率进行验证,并对不同权重取值在实际应用中的适用性和可靠性进行分析。 在模拟试验中,根据参与运算的模拟等高线节点序列中所包含的节点个数n、m,取δ=[min(n,m)/5],ε取参与运算的两个特征描述序列标准差最小值,即ε=min(σ1,σ2),特征描述测度函数中曲率测度的权值λ=0.5。 模拟试验1:经过粗匹配后,当一条原始等高线有两条或多条候选匹配等高线时,如图6所示,原始等高线A与等高线B1、B2空间位置邻近,且高程值均相等,需首先基于特征描述测度函数将等高线A与B1、B2转化为特征描述序列,再分别计算A与B1、B2的相似度,根据相似性的量化度量结果进一步实施精匹配。分别采用本文提出的CANV测度与单一弦长测度、单一夹角测度对等高线相似性进行量化度量。由表1所示试验结果可知,A与B1的相似度大于A与B2的相似度,因而A应与B1匹配,这一结果与人的空间认知结果相符。对基于3种不同测度的相似性度量结果进行对比分析,发现基于本文提出的CANV测度的量化度量结果具有更大的相似度较差,说明CANV测度能够对等高线的相似程度提供更显著的数值上的区分。模拟试验1表明,本文策略适用于具有多条候选等高线的多源等高线匹配情况,且本文提出的CANV测度较单一测度能够对相似程度提供更显著的区分效果。 表1 模拟试验1结果 模拟试验2:在图幅边界和地形变化较大区域,可能存在一条原始等高线与多条待匹配等高线匹配情况。当待匹配等高线集中的多条等高线与原始等高线相似度较差很小时,须考虑这些等高线可能是非闭合情况下原始等高线的不同部分(如图7(a))或是由于地形变化造成的等高线拆分(如图7(b)),需利用其他空间特征信息进一步辅助判断。 线群密度、曲折系数及曲线长度等是描述空间线状要素几何特征的主要指标[13]。本文以曲线长度作为辅助判断指标,对图7(a)、图7(b)中的两组模拟数据依曲线长度公式分别计算A、B1、B2的长度及与A的相似度,获得表2、表3所示结果。由表2可知,原始等高线A与待匹配等高线B1、B2的相似度较差为0.095 3,较差较小,且LB1+LB2≈LA,据此可判断图7(a)中的B1、B2均为A的同名等高线。由表3可知,原始等高线A与待匹配等高线B1、B2的相似度较差为0.065 2,较差较小,且LB1+LB2≈LA,因此图7(b)中的B1、B2均为A的同名等高线。由模拟试验2可知,本文方法在等高线非闭合以及等高线拆分情况下仍适用,并且能够结合其他辅助判断指标识别存在多条同名等高线的情况,实现一对多匹配。 表2 模拟试验2(a)结果 表3 模拟试验2(b)结果 模拟试验3:当等高线分布密集或原始等高线与待匹配等高线局部差异较大时,会出现如图8所示的原始等高线与异名等高线间的欧氏距离小于其与同名等高线间的欧氏距离的情况,此时利用已有的基于欧氏距离的相似度计算方法可能造成误匹配。 本文分别用传统Fréchet距离方法、文献[18]提出的平均Fréchet距离法和本文方法对图8中的A与B1、B2进行匹配,获得如表4所示结果。传统Fréchet距离法和平均Fréchet距离法计算结果均显示A与B2之间距离小于A与B1之间距离,按照文献[14]和文献[18]提出的匹配策略,A应与B2匹配。然而,由图8可知,A与B1在形状上更为相似。利用本文方法计算得到A与B1相似度为0.527 3,大于A与B2相似度0.200 0,A应与B1匹配,这一匹配结果与人的空间认知相符。同时,对3种方法运行效率的模拟结果显示,本文方法较传统Fréchet距离和平均Fréchet距离方法具有更好的运算效率。模拟试验3表明,当地形变化导致原始等高线邻近范围内出现干扰要素时,基于欧氏距离的相似性度量方法可能出现度量误差,导致误匹配情况。而本文方法由于顾及了等高线之间几何形态上的相似特征,能够对异同名等高线进行更有效区分,并保证较高的运算效率。 表4 模拟试验3结果 本文获取了如图9所示法国某地2000年SRTM合成孔径雷达90 m分辨率DEM数据和该地区2009年ASTER GDEM光学30 m分辨率DEM数据,分别生成如图10所示的起始高程值相等的50 m等高距等高线,高程范围约为50~1600 m。由于成像时间、传感器和高程精度的不同,两种DEM生成的同一地区等高线在几何形态和空间位置上会存在一定差异。由于在高程精度和现势性方面ASTER GDEM数据优于SRTM数据,因此以SRTM生成等高线作为原始等高线,以ASTER GDEM生成等高线作为待匹配等高线,利用本文方法对两种等高线数据进行匹配,对匹配精度和运行效率分析,并对不同权重取值对匹配结果的影响进行比较。 基于本文提出的等高线匹配策略,首先根据数据特点,构建原始等高线缓冲区,按照空间位置相近及高程值相等的原则进行粗匹配,生成精匹配数据集,针对存在多条候选匹配等高线的原始等高线,进一步实施精匹配: (1) 基于CANV测度函数,利用式(5)将等高线二维节点序列转化为一维特征描述序列。 (2) 确定控制参数,利用式(7)求解特征描述序列之间的最长公共子序列。为了保证运算效率,δ取值不宜过大。本文根据原始等高线以及待匹配等高线节点序列中所包含的节点个数n、m,取δ=[min(n,m)/10];基于特征描述序列的固有特征,ε则取两描述序列标准差最小值,即ε=min(σ1,σ2)。 (3) 利用式(8)计算原始等高线与其精匹配集内待匹配等高线的相似度。 (4) 依据相似度计算结果进行同名等高线匹配,若存在无法判断情况,需依据其他空间特征指标辅助判断。 基于上述步骤实现多源等高线匹配(图11),对匹配精度、运行效率及不同权重取值对试验结果的影响进行评估和对比,获得表5、表6及图12所示结果。 (1) 为了对匹配结果进行评价,对λ=0.6时的匹配精度进行了检查,并利用文献[29]的评价公式(9)对结果进行评估,如表5所示。 (9) 根据表5所示的试验结果统计信息,在试验区域内,本文方法具有较高的匹配召回率和匹配准确率,并能够保证较好的运算效率。本文将运行时间随等高线包含节点数量的变化情况绘制于图12。由结果可知,等高线匹配耗时随着等高线包含节点个数的增加而增加,但当等高线包含节点个数过多时,会由于地形细节形态过多而出现匹配耗时过长、效率降低的问题,因而本文对包含节点数量过多的等高线进行特征点提取以保证运算效率。但由于特征点提取本身具有运算代价,同时还存在提取质量和精度的问题,会导致误匹配和匹配失败情况,这也是本次试验中匹配召回率和准确率降低的原因之一。因此在面向具体应用时需要利用大量数据进行充分试验,将等高线所包含的节点个数限制在合理范围内进而保证匹配效率和精度。 (2) 为验证不同权重取值对匹配结果的影响,对λ取0~1范围内不同值时匹配准确率及召回率进行了比较,获得如表6所示结果。通过对比分析可知,当λ取0~1范围内不同值时匹配准确率均为90%~92%,召回率为87%~88%,并没有显著差异,说明本文所提出的CANV测度能够保证较高的匹配准确率,且λ取值对匹配结果的精度影响并不显著,在本试验区内λ=0.6时匹配精度相对较高。 图5 基于控制参数的最长公共子序列求解Fig.5 The longest common subsequence solution based on control parameters 图6 原始等高线与待匹配等高线Fig.6 A primitive contour with several contours to be matched 图7 一对多匹配情况Fig.7 The one-to-many contours matching 图8 等高线距离相近但形状不相似Fig.8 Contours are close in Euclidean distance but in different shapes 图9 原始DEM数据Fig.9 Original DEM datasets 图10 DEM生成等高线数据Fig.10 Contours generated from DEM datasets 图11 真实数据匹配结果Fig.11 The matching result of real datasets 综上所述,在合理的参数取值和计算能力范围内利用本文方法进行等高线匹配具有较高匹配精度,且能够保证良好的运行效率。 表5 λ=0.6时结果精度评价 表6 λ取不同值时匹配精度对比 图12 运行时间随等高线节点数量变化Fig.12 The running time changing with the number of contour nodes diagram 等高线匹配是地图更新、制图综合以及数据融合的重要环节之一,已有的基于拓扑关系构建的匹配方法和基于欧氏距离的相似度计算方法,由于未顾及等高线的几何形态特征,导致在匹配过程中可能产生误匹配情况。本文提出一种顾及几何特征相似性的基于最长公共子序列的多源等高线匹配策略,以空间几何形态特征描述为目标,提出了基于节点曲率以及法向量与横坐标轴夹角的混合特征描述测度(CANV),将等高线节点序列转化为几何形态特征描述序列,利用模拟数据和真实数据对本文方法的适用性、准确率及运行效率进行了验证,并对参数取值以及不同测度对等高线的相似度区分效果进行了对比。试验结果表明,与已有方法相比,本文匹配策略顾及了等高线空间位置特征和几何形态特征,在等高线密集、非闭合区域以及变化剧烈区域具有较好的适用性和可靠性,能够有效降低多源等高线数据匹配误差,并保证较好的运行效率。 然而,本文所提出的匹配策略主要基于等高线空间位置和几何形态特征,在基于相似度的匹配过程中并未考虑等高线群构成的地形特征以及地貌变化规律,因而在匹配过程中仍然存在误匹配情况。顾及地形特征的特征点提取、参数设置以及匹配规则的进一步完善,将有助于提高多源等高线匹配精度和自动化程度,也是后续研究的重点内容。2 试验与分析
2.1 模拟试验
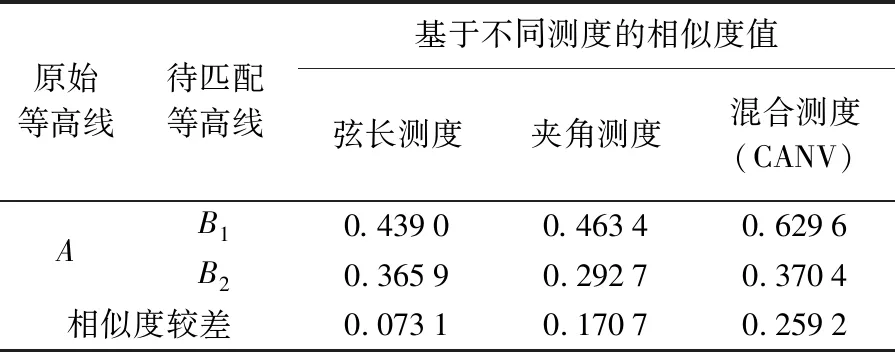
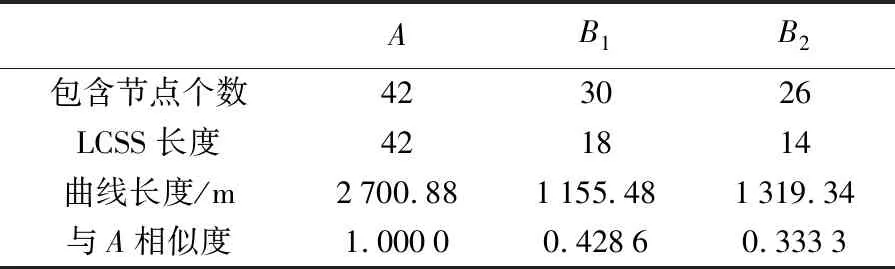
2.2 真实数据试验





3 结 论
