不规则三角网数字水深模型缓冲面快速构建的滚动球加速优化算法

董 箭，张志衡，彭认灿，李改肖，王 沫

1. 海军大连舰艇学院军事海洋与测绘系，辽宁 大连 116018； 2. 海军大连舰艇学院海洋测绘工程军队重点实验室，辽宁 大连 116018

数字水深模型(DDM)是反映水深变化的数字化模型，也是用深度表达海底地形特征的一种常用数字模型，根据水深点数据组织方式的不同，分为规则格网DDM(GRID_DDM)和不规则三角网DDM(TIN_DDM)[1-6]。缓冲区分析是二维GIS空间分析的基本功能，是确定二维地理实体的空间邻近度或影响范围的重要手段[7-9]。三维条件下的缓冲区分析称为缓冲体分析，由于DDM所固有的单值曲面特性，其缓冲体分析又被称为缓冲面分析[10-11]。近年来，随着人类对海底世界的全方位加速探索，应用面向海底三维空间分析的DDM缓冲面构建技术对于解决海底污染源扩散、水下潜航器航行安全保障、海底矿藏分布探明和海底地形多尺度表达等问题具有重要的理论和现实意义[11-19]。

目前有关三维缓冲体构建算法的研究主要包括矢量算法和栅格算法两类[10-13,20-23]。矢量算法所构建的缓冲体精度较高，但其涉及大量的三维空间几何求交运算，复杂度较高，运行效率较低[10-13]。文献[12]通过对布尔运算拓扑关系完整性、逻辑判断一致性及运算容差统一性的条件约束，提出了一种基于高效布尔运算的三维矢量缓冲区生成算法，然而布尔运算的构建机理决定了该算法受目标实体复杂度及采样点拓扑关系的影响较大，算法时间复杂度相对较高。文献[13]利用带符号的欧氏距离变换技术及缓冲半径对目标模型离散化后的体素进行缓冲控制点的条件筛选，结合隐式曲面重构模型构建三维缓冲区的参考曲面，提出了一种基于空间填充思想的三维缓冲区分析算法，由于体素拓扑关系维护及隐式曲面重构过程相对复杂，算法效率较低。栅格算法主要采用三维欧氏距离变换方法，实现了对各类地理要素的三维缓冲体构建，与矢量算法相比，其算法简单且较易实现，运行效率较高。但此类算法只针对于栅格数据，适用范围较窄且所构建的缓冲体精度较低[10-11,20-23]。文献[11]针对单值曲面这类特殊的地理要素，提出了一种基于滚动球模型的单值曲面缓冲体边界生成算法，通过单值曲面逻辑并运算法则的构造，避免了栅格采样点距离场的重复计算，算法时间复杂度降至O(nr2)。文献[20]利用三维欧氏距离的递推延续性质，将栅格曲面的三维欧氏距离变换分解为n个n×n的像素点(栅格单元)的二维二值图像的二维欧式距离变换过程来构建缓冲体，算法复杂度为O(n6)。文献[22]通过优化方法减少需要参与距离计算和比较的二维图像个数与二维图像中特征点的个数，使算法的时间复杂度降至O(n3lgn)。文献[23]设计了一种体元信息由生长元向周围邻域传递的等值面扩张路径，提出了一种基于桶数据结构的栅格三维缓冲体生成算法，时间复杂度为O(V)(V为体元个数)。

与GRID_DDM相比，由于TIN_DDM采用原始采样点作为模型数据，可以更好地反映海底地形地貌(如山脊、山谷、地形断裂线等)，对起伏程度较大区域的地形描述更加精细，也更加有利于提高缓冲面分析结论的准确性[1-2]。然而，当前三维缓冲体构建的算法研究大部分为栅格算法，主要针对GRID_DDM而无法直接应用于TIN_DDM。研究较少的矢量算法虽可以应用于TIN_DDM，但构建过程中需要大量处理复杂的三维空间几何求交运算，算法运算效率较低，且最终构建的矢量缓冲面难以存储和表达。

为解决现有三维缓冲体构建算法在处理TIN_DDM这类特殊地理空间要素时存在的模型精度与算法效率这一矛盾问题，本文将GRID_DDM缓冲面构建的滚动球模型应用扩展至TIN_DDM缓冲面的构建过程，建立了滚动球半径阈值关联的缓冲面精度定量调控模型，分析论证了关键采样点判定准则与滚动球半径的数值关联关系，提出了TIN_DDM缓冲面快速构建的滚动球加速优化算法，实现了大数据量TIN_DDM缓冲面的多次快速构建。

1 滚动球模型在TIN_DDM缓冲面构建中的应用扩展及局限性分析

1.1 基于TIN_DDM的滚动球模型构建

滚动圆变换是当前自动生成二维线或面要素缓冲区边界的通用算法，其实质是对组成二维线或面要素的无限个采样点的缓冲区求并而获得二维线或面要素的缓冲区边界[7,11]。文献[11]在栅格算法的基础上，针对GRID_DDM这类单值曲面，对滚动圆进行三维扩展，提出滚动球模型构建原理，采用与滚动圆变换类似的方法自动获得三维空间单值曲面要素的缓冲面，所提模型主要依据三维缓冲体边界的数学定义和单值曲面的特性进行三维缓冲面构建。

由文献[11]可知，三维缓冲体边界的数学定义为

B(T,r)={P(x,y,z)|{dmin(P,QT)|QT(xT,yT,zT)∈T}=r}

(1)

式中，B(T,r)表示地理要素T的缓冲半径为r的缓冲体边界;P(x,y,z)表示缓冲体边界B(T,r)上的任意一点;QT(xT,yT,zT)表示地理要素T上任意采样点;dmin(P,QT)表示缓冲体边界B(T,r)上的P点至地理要素T上各个QT点间的三维欧氏距离最小值。

基于上述三维缓冲体边界概念，三维缓冲体边界等价于地理要素T上无限个采样点的等距离球面的并集。但对于由有限个离散水深采样点构成的DDM，若在保证缓冲面构建精度的前提下，三维缓冲面可等价于DDM上有限个水深采样点的等距离球面的并集。然而，等距离球面并集的计算涉及大量三维空间几何求交运算，效率相对低下，且所生成的上下缓冲面存储与表达均较为困难。为提高算法运行效率，文献[11]针对GRID_DDM这类特殊单值曲面，提出一种基于栅格算法的单值曲面逻辑并运算法则。该运算法则为：GRID_DDM采样点间上(下)缓冲面的并集运算可简化为各自上(下)缓冲面在z轴方向上的极大(小)取值过程，即可通过GRID_DDM采样点及周围各个离散水深点的等距离球面在采样点z轴方向交点的极大(小)值来确定该采样点对于的上(下)缓冲面点。滚动球模型中的单值曲面逻辑并运算法则通过单一坐标轴方向的数值比较实现了三维空间几何求交的运算简化，具有较高的算法运算效率，且算法本身对DDM数据类型的依赖性较小。由此，本文提出将滚动球模型应用进一步扩展至TIN_DDM缓冲面构建过程的设想，其具体实施步骤为：①采用矢量算法精确计算各个采样点的等距离球面；②利用基于栅格算法的单值曲面逻辑并运算法则依次计算各个采样点在z轴方向上的上(下)缓冲面点坐标；③以三角网形式对TIN_DDM上(下)缓冲面进行存储和表达。尽管上述算法设想在理论层面上可较好地解决TIN_DDM缓冲面构建算法运算效率低下及生成缓冲面的存储与表达方面的问题，但实际应用中滚动球模型在构建过程中仍存在一定的精度与效率方面的矛盾。因此，需进一步分析论证滚动球模型在TIN_DDM缓冲面构建过程中的精度与效率局限性，设计并提出相应的模型优化方案，以满足当前TIN_DDM缓冲面构建的实际应用需求。

1.2 滚动球模型在TIN_DDM缓冲面构建中的精度局限性分析

滚动球模型在TIN_DDM缓冲面构建过程中的精度损失主要体现在以下两个方面：①由于采用TIN_DDM上有限个水深采样点的等距离球面进行求交运算来构建矢量缓冲面，导致所构建的矢量缓冲面与TIN_DDM的三角网面之间并不严格满足三维缓冲体边界的数学定义，存在模型构建原理上的精度缺陷；②为提高模型运算效率，采用基于栅格算法的单值曲面逻辑并运算法则对各个等距离球面进行求交运算，其本质为对所构建的TIN_DDM矢量缓冲面进行三角网格化处理，以便于生成缓冲面的存储与表达，尽管在一定程度上简化了模型的计算过程，但同时也造成了模型构建过程中的精度损失。

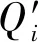
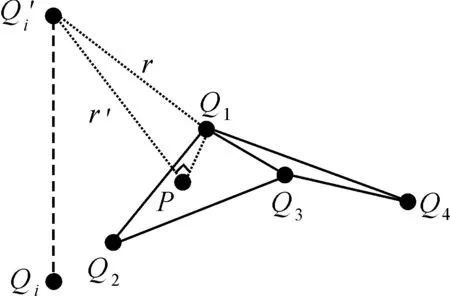
图1 TIN_DDM矢量缓冲面构建过程中的模型精度分析Fig.1 The situation of model precision analysis during the construction of TIN_DDM vector butter surface

(2)

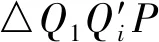
(3)

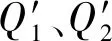
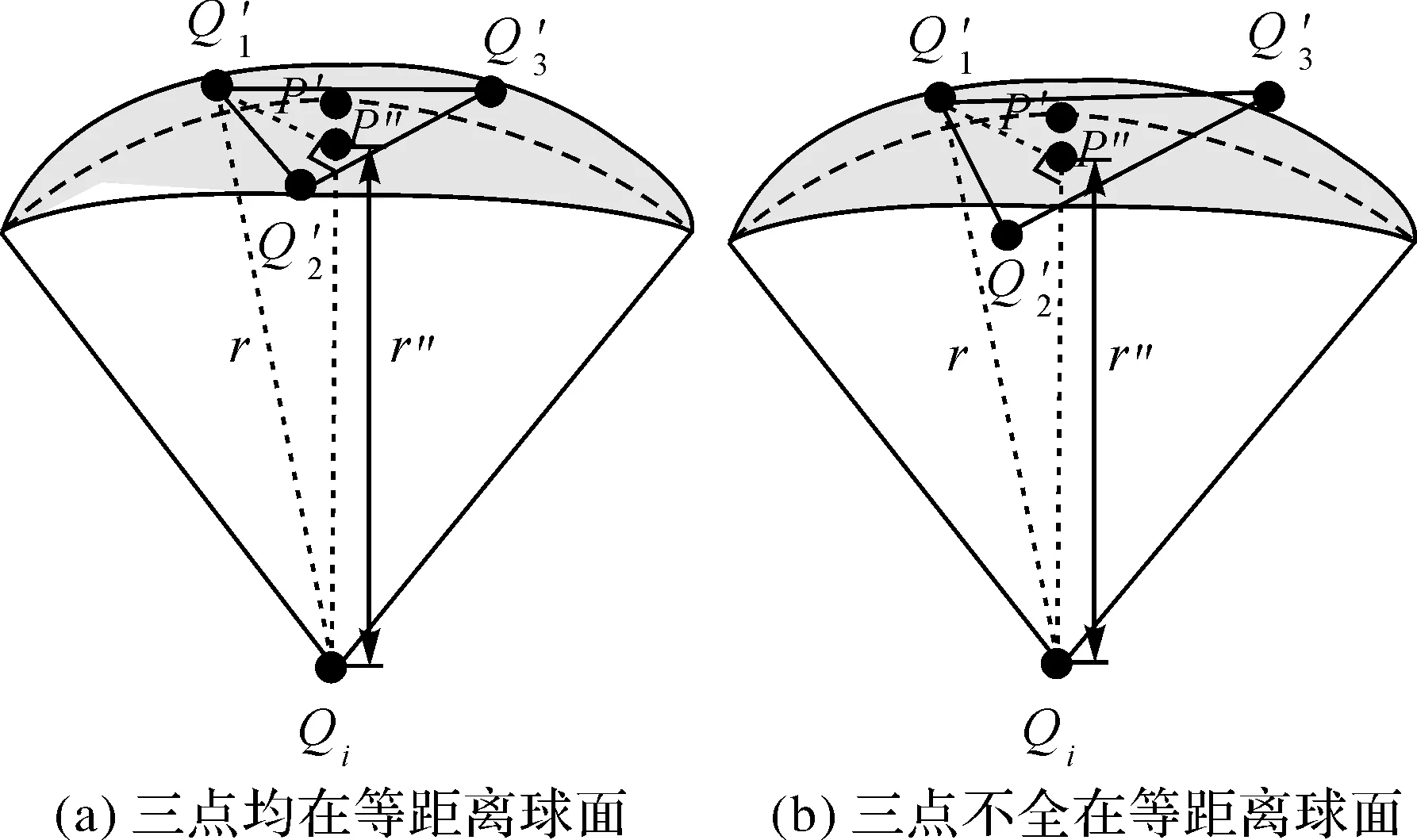
图2 TIN_DDM矢量缓冲面三角网格化过程中的模型精度分析Fig.2 The situation of model precision analysis during the triangulation of TIN_DDM vector butter surface

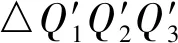
(4)

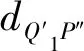
(5)

基于上述分析，采用滚动球模型所构建的TIN_DDM缓冲面上各点与真实TIN_DDM缓冲面之间的误差最大值ωmax为

(6)

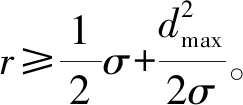
1.3 滚动球模型在TIN_DDM缓冲面构建中的效率局限性分析

评定算法优劣性的指标主要为算法精度和运算效率。在GIS实际应用中，当算法精度满足应用需求时，对于TIN_DDM这类数据量较大的模型，算法执行效率将显得尤为重要。由1.1节中基于TIN_DDM的滚动球模型构建过程可知，TIN_DDM缓冲面构建的关键在于其上各点z坐标值的计算，而缓冲面上各点z坐标值的确定主要通过借鉴文献[11]中所提的基于栅格算法的单值曲面逻辑并运算法则进行计算。假设TIN_DDM中水深采样点的个数为n且各点均匀分布(分布密度为ρ)，则对于其中每个水深采样点所对应的缓冲面点的z坐标值，均需要遍历滚动球在XOY平面覆盖范围内的水深点(水深点个数n′=ρπr2)，并判断各个采样点的等距离球面是否在所选水深采样点的z轴方向上形成极值。从而，对于每个水深采样点需进行ρπr2次计算，整个TIN_DDM缓冲面的构建过程需进行nρπr2次运算，即算法的时间复杂度为O(nr2)。

随着多波束等先进水深测量设备的广泛运用，TIN_DDM中包含的水深采样点数量日益剧增，单次多波束水深测量获得的采样点数据量可达百万甚至千万级别。水深采样点数据量的日益剧增尽管有利于海底地形的精细化表达，但同时也决定了进行TIN_DDM缓冲面构建的时间成本巨大。此外，考虑到不同行业不同层次的应用需求，实践中往往需要利用不同缓冲半径多次构建TIN_DDM缓冲面，这对TIN_DDM缓冲面构建算法的效率提出了更为严格的效率要求。因此，需进一步探索影响TIN_DDM缓冲面构建效率的关键因素及其内在关联，简化算法流程，避免冗余运算，以实现面向TIN_DDM缓冲面构建的滚动球模型进行加速优化。

2 面向TIN_DDM缓冲面构建的滚动球加速优化模型

2.1 TIN_DDM缓冲面构建关键采样点判定准则及步骤

栅格条件下单值曲面逻辑并运算法则以一维条件下的数值比较运算对TIN_DDM采样点等距离面的曲面求交运算进行了等效简化，实现了给定缓冲半径条件下TIN_DDM缓冲面的快速构建。需要指出的是，该法则的运用并未实质性地减少参与等距离面构建的TIN_DDM采样点数量，对于工程实践中可能出现的高密度TIN_DDM缓冲面多次重复构建应用，缓冲半径对算法时间复杂度的数值影响会逐渐增强，成为制约算法执行效率的主要因素。因此，以缓冲半径为关联纽带，分析和论证有效参与TIN_DDM缓冲面构建的关键采样点与算法时间复杂度间的关联关系，构建缓冲半径不相关的TIN_DDM缓冲面加速构建算法成为解决高密度TIN_DDM缓冲面多次重复构建效率问题的技术前提。

栅格条件下单值曲面逻辑并运算法则需对每个TIN_DDM采样点进行ρπr2次计算，以此确定该TIN_DDM采样点对应的缓冲面边界点。然而，一方面，栅格条件下单值曲面逻辑并运算法则的极值特性决定了该缓冲面边界点必然唯一存在其至TIN_DDM距离等于缓冲半径的关键采样点，且两者间距离为该缓冲面边界点至TIN_DDM采样点间的最小值；另一方面，栅格条件下单值曲面逻辑并运算法则的极值特性也证明了任意TIN_DDM采样点对应缓冲面边界点解算过程中的ρπr2次计算，可由该采样点与其对应的关键采样点间(实际有效参与缓冲面构建的采样点)的一次数值计算等效替代。由此，准确快速判定任意缓冲面边界点至TIN_DDM距离等于缓冲半径的关键采样点成为减少冗余等距离球面求交运算，提高算法执行效率的核心问题。如图3所示，曲面T为单值曲面地理要素；曲面B1为曲面T的上缓冲面；Qi、Q1和Q2点分别为单值曲面地理要素T上的三点；L1L2为Qi点的z轴方向；P′点为以Q1采样点为球心的等距离球面在L1L2方向上形成极大值点；P′点至Q1点的距离为滚动球半径r；P′点至Q2点的距离为d。

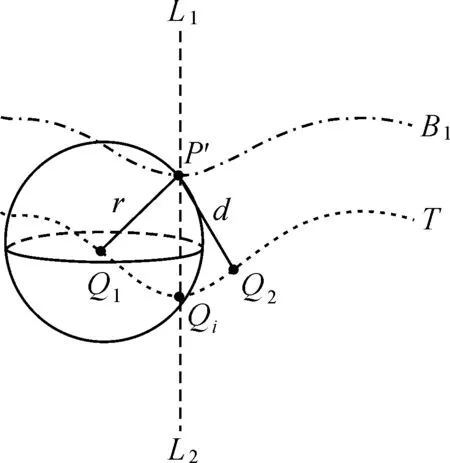
图3 TIN_DDM缓冲面构建关键采样点Fig.3 The situation of the key point during TIN_DDM butter surface construction

图3中，由于P′点为Q1采样点的等距离球面在L1L2方向上所形成的极大值点，则单值曲面地理要素T上其余采样点的等距离球面在L1L2方向的交点均位于P′点之下。对于曲面T上与Q1点相异的任意一点Q2而言，则P′点至Q2点的距离d始终大于滚动球半径r，即Q1点为P′点在曲面T上的最近点(且距离等于滚动球半径r)。因此，在上(下)缓冲面点z轴方向上形成极大(小)值的等距离球面所对应的球心采样点即为该上(下)缓冲面点所对应的TIN_DDM上的最近点(即TIN_DDM缓冲面构建的关键采样点)。基于上述分析，本文提出如下TIN_DDM缓冲面构建关键采样点判定步骤：

(1) 以r为滚动球半径，依次构建TIN_DDM中各水深采样点Qi的等距离球面。

(2) 判断各个等距离球面是否在水深采样点Qi的z轴方向上形成极大(小)值。

(3) 以形成极大(小)值的等距离球面所对应的球心采样点标记为采样点Qi的上(下)缓冲面点所对应的TIN_DDM上(下)缓冲面构建关键采样点。

2.2 TIN_DDM缓冲面构建关键采样点与滚动球半径的数值关联性分析

由2.1节中分析可知，滚动球半径r与TIN_DDM缓冲面构建关键采样点的判定具有一定的关联关系。一般情况下，当滚动球半径r发生变化时，需重复前述步骤依次判定TIN_DDM缓冲面构建的关键采样点，并构建新的TIN_DDM缓冲面。这对于大数据量条件下的TIN_DDM应用不同缓冲半径进行多次重复缓冲面构建的实际应用而言，显然难以满足其效率需求。考虑到滚动球半径的取值具有连续有界的变化规律，且在滚动球半径变化不大的条件下，TIN_DDM缓冲面构建关键采样点的判定结论具有一定相似性。因此，需进一步分析滚动球半径连续变化条件下TIN_DDM缓冲面构建关键采样点判定结论的变化趋势，建立滚动球半径与TIN_DDM缓冲面构建关键采样点的数值关联关系，构建面向TIN_DDM缓冲面构建的滚动球加速优化模型，实现滚动球半径变化弱相关的TIN_DDM缓冲面高效构建算法。

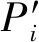
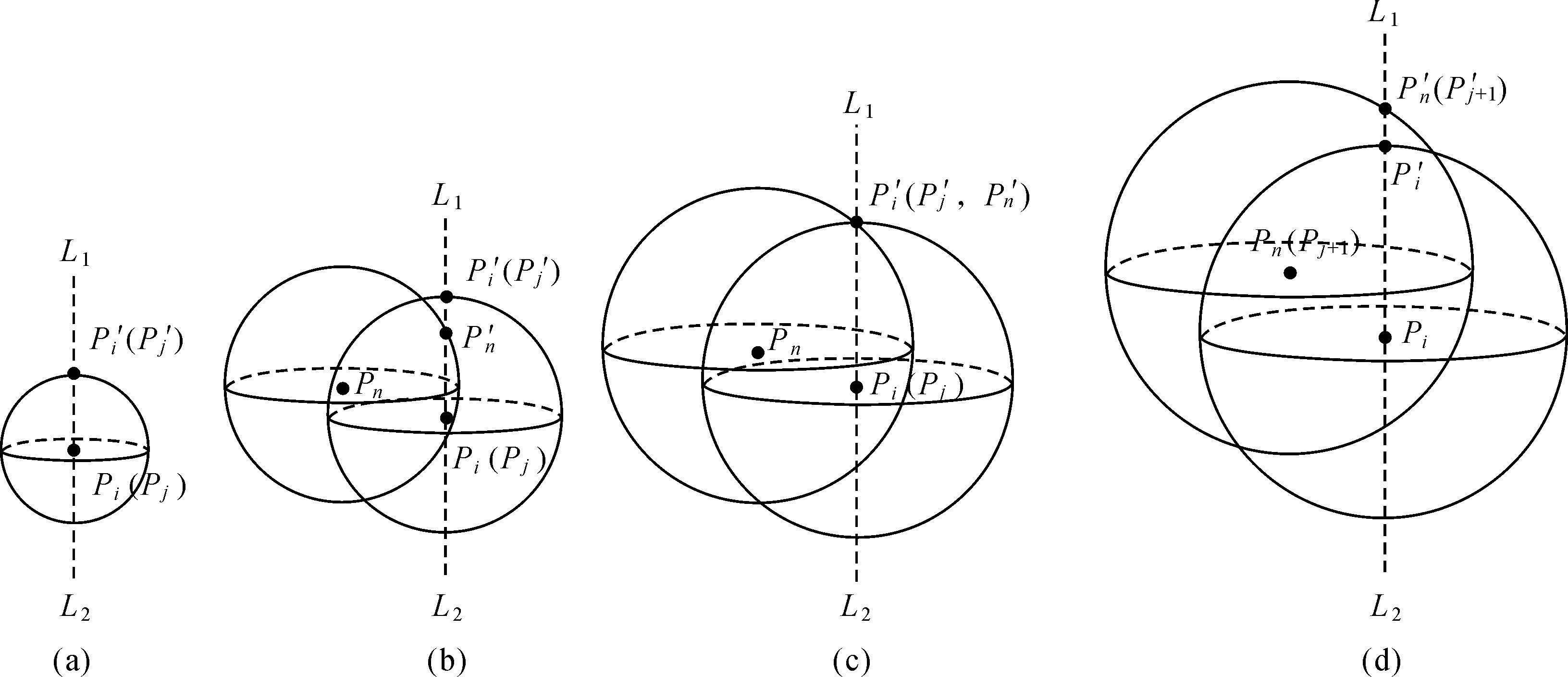
图4 TIN_DDM缓冲面构建关键采样点与滚动球半径的数值关联性分析Fig.4 The situation of numerical correlation analysis between the key point during TIN_DDM butter surface construction and the roll radius

图4(a)中，当滚动球半径r从0开始变化时，采样点Pi的z轴方向上形成极值点的等距离球面所对应的构建关键采样点同样为采样点Pi，即此时构建关键采样点Pj与采样点Pi为同一点。如图4(b)所示，随着滚动球半径r的逐渐增大，采样点Pi的邻域内必然存在一定数量的采样点等距离球面与Pi点的z轴方向(L1L2方向)相交。

(7)

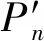
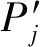
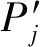
(8)

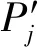
对TIN_DDM中所有采样点所对应的TIN_DDM缓冲面构建关键采样点与滚动球半径的数值关联性进行分析，将其记录在如图5所示的TIN_DDM上缓冲面构建关键采样点与滚动球半径的数值关联性数据链中。其中P1至Pl为TIN_DDM中的各水深采样点；j1至jl为各水深采样点所对应的TIN_DDM缓冲面构建关键采样点个数；0rl1rl2…rljl表示各TIN_DDM缓冲面构建关键采样点的滚动球半径范围临界值；Pl1Pl2…Pljl表示各半径范围所对应的TIN_DDM缓冲面构建关键采样点。

采用上述面向TIN_DDM缓冲面构建的滚动球加速优化模型，通过对TIN_DDM进行前期预处理，建立TIN_DDM缓冲面构建关键采样点与滚动球半径之间的数值关联性数据链，对面向TIN_DDM缓冲面构建的滚动球模型进行加速优化。在后期应用中，只需进行简单查询即可实现任意缓冲半径条件下TIN_DDM缓冲面的快速构建，算法时间复杂度降至O(n)，可满足不同行业不同层次对于利用不同缓冲半径多次构建TIN_DDM缓冲面的应用效率需求。

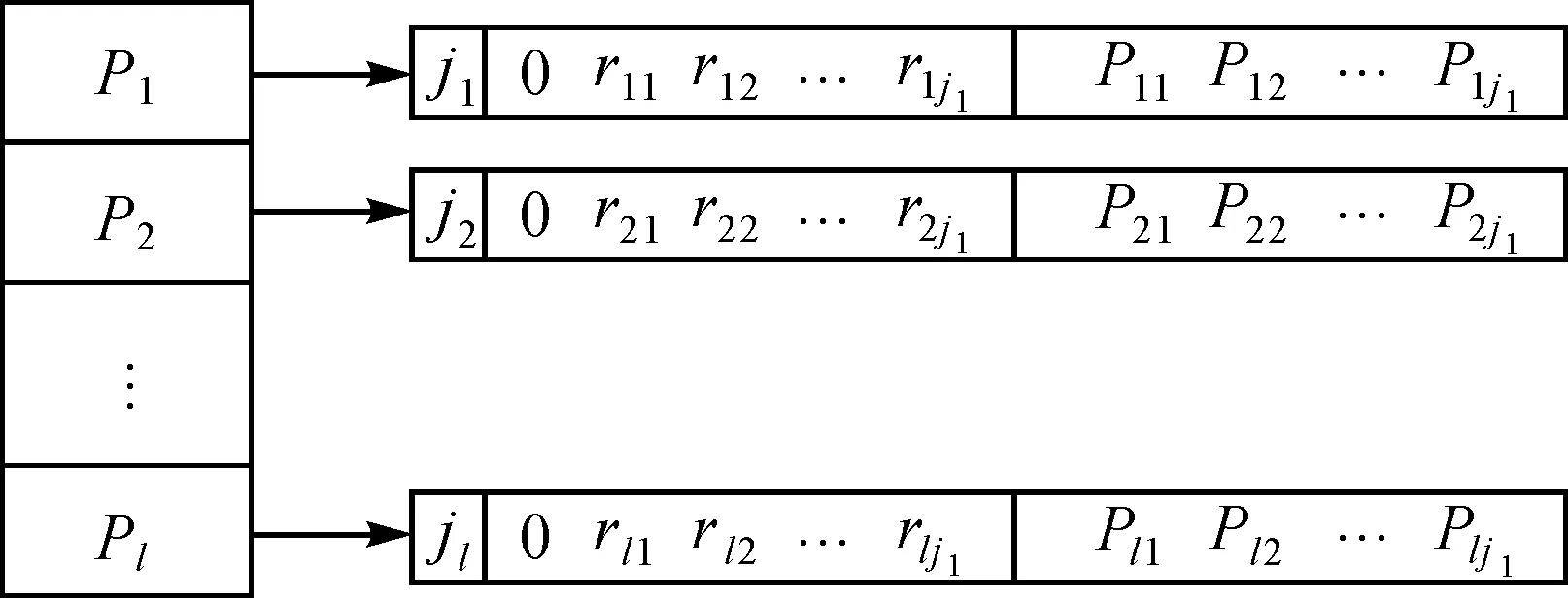
图5 TIN_DDM缓冲面构建关键采样点与滚动球半径的数值关联性数据链Fig.5 The situation of numerical correlation data link between the key point during TIN_DDM butter surface construction and the roll radius

3 试验结果与分析

为验证算法的可行性，本文通过Matlab编程实现了基于滚动球模型的TIN_DDM缓冲面构建算法(以下简称算法Ⅰ)和基于滚动球加速优化模型的TIN_DDM缓冲面快速构建算法(以下简称算法Ⅱ)，并利用Matlab的三维显示功能对两类算法的试验结果进行了可视化显示与分析。

试验所采用的数据为我国东海某海区的不规则三角网数字水深模型的水深数据，共包含12 477个水深点；试验环境为Inter(R)core(TM)i3处理器，主频为3.4 GHz，内存为2 G。采用两种算法分别对原始TIN_DDM海底地形表面构建缓冲半径为500、1000、1500、2000、2500和3000 m的缓冲面，利用Matlab程序对各缓冲半径的上下缓冲面的空间三角网进行可视化显示并利用Surfer8.0软件绘制各数据等深距为5m的等深线图，试验结果如表1所示。图中红方框所圈区域为TIN_DDM海底地形表面及其上下缓冲面所对应的凹地形区域，红椭圆圈所圈区域为TIN_DDM海底地形表面及其上下缓冲面所对应的凸地形区域。

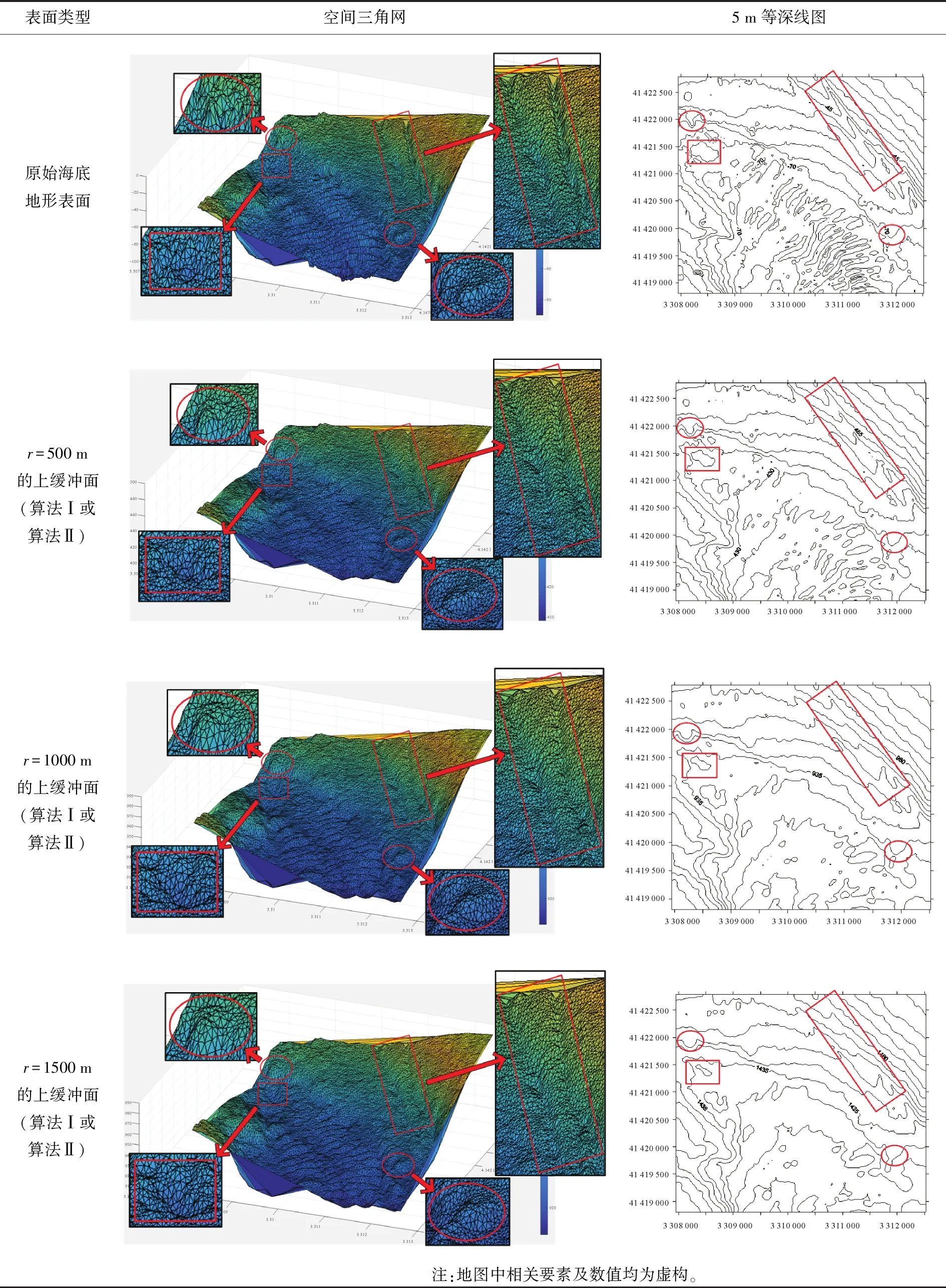
表1 试验结果分析

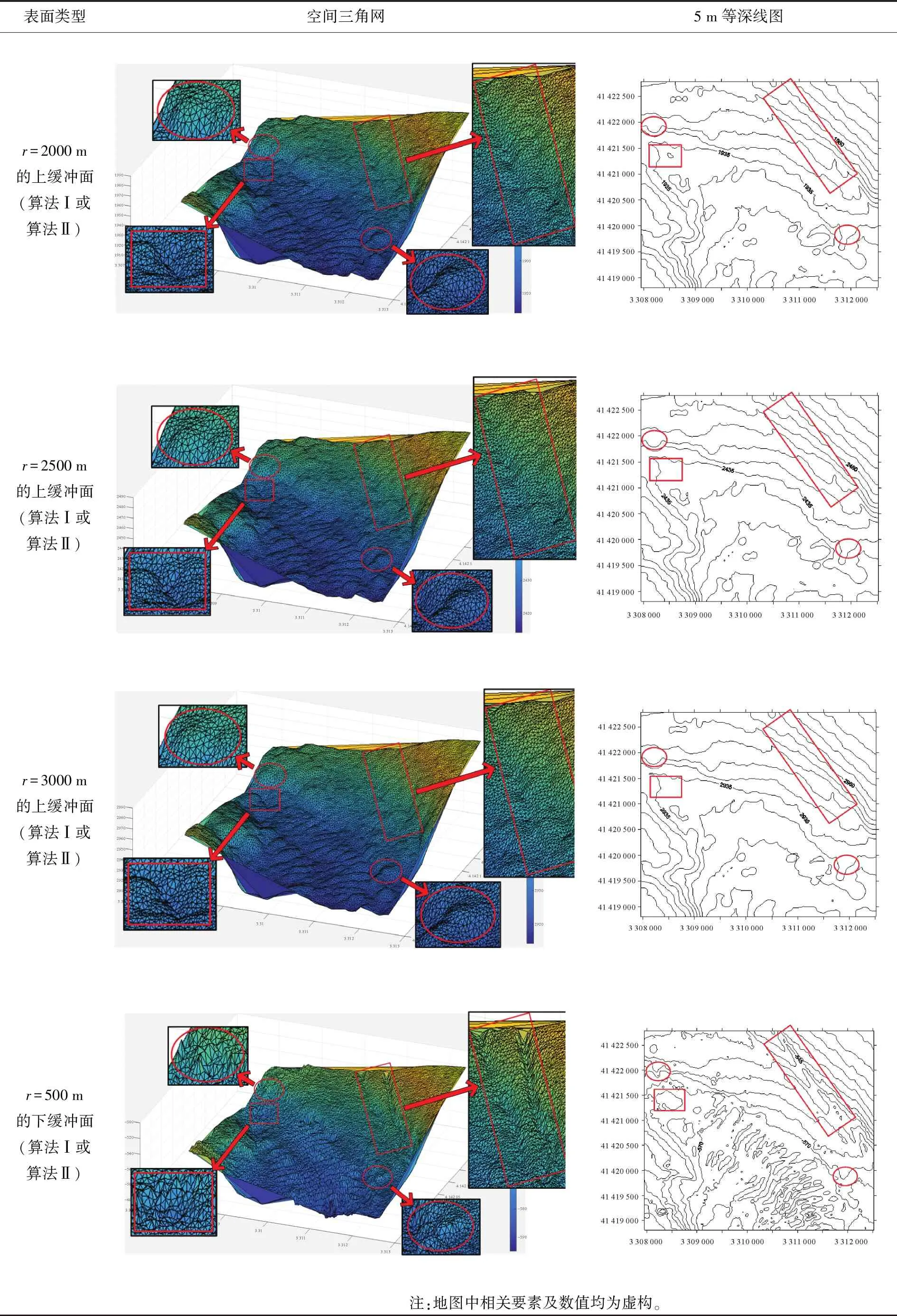
续表1

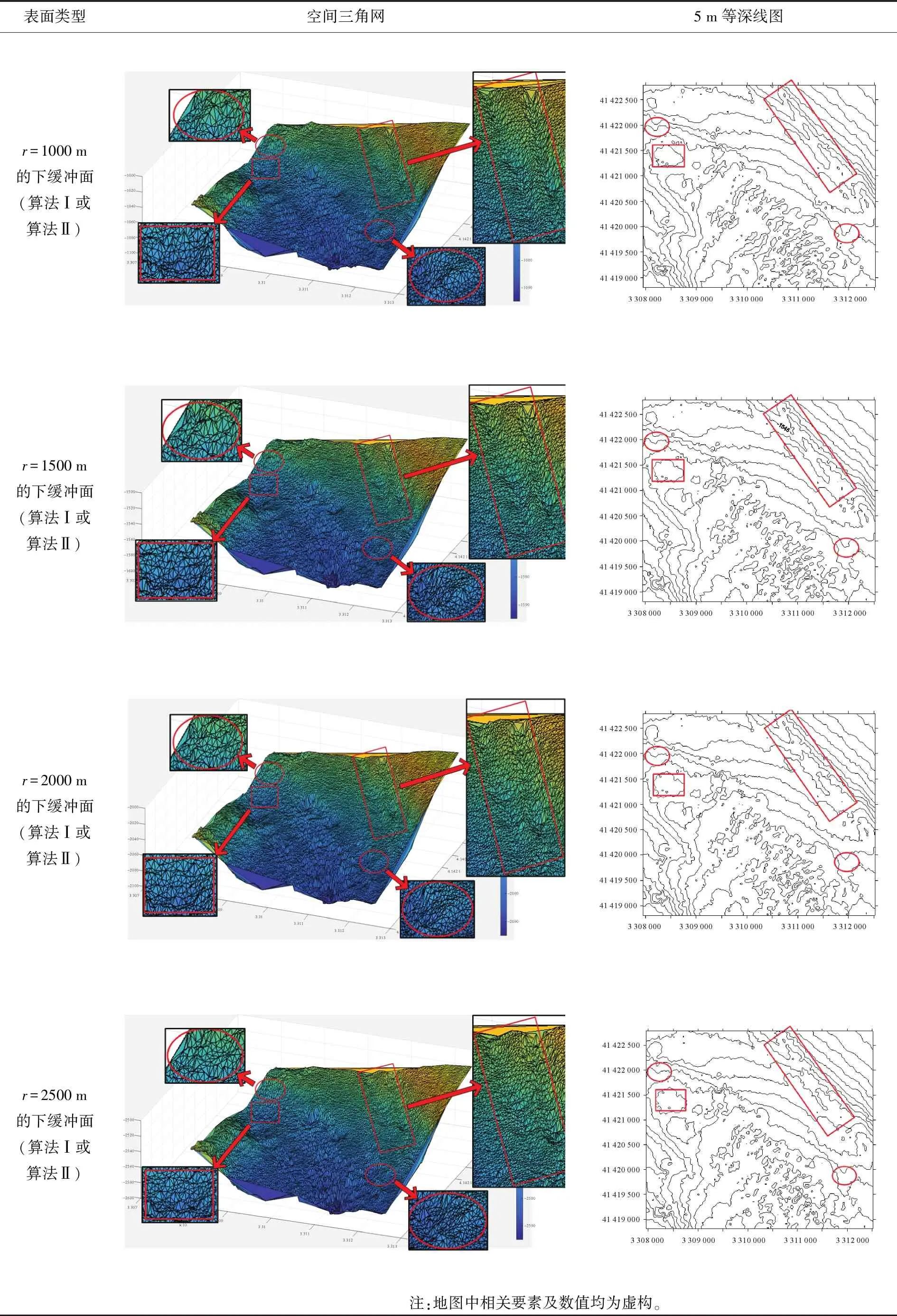
续表1

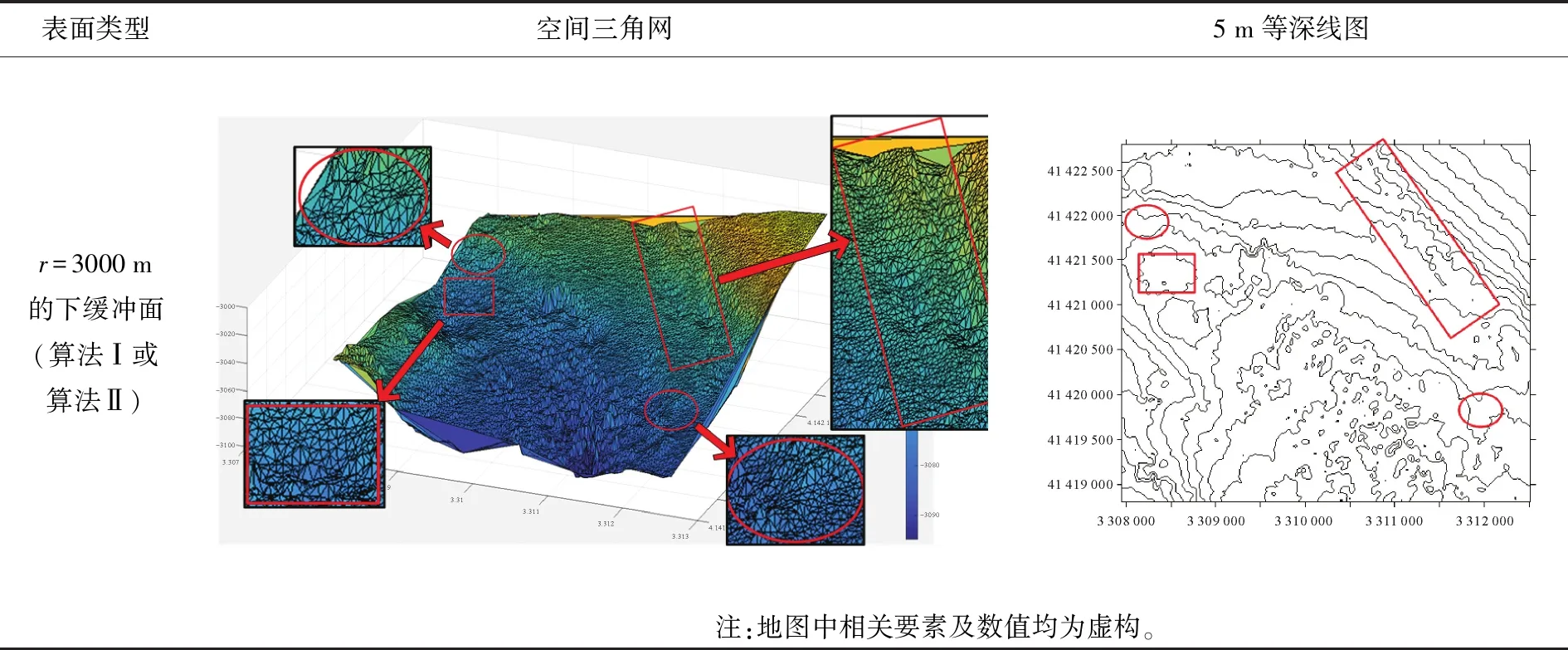
续表1

试验结果表明：①算法Ⅰ与算法Ⅱ的试验结果相同；②上缓冲面的凹地形区域均有被填平或缩小的趋势，且随着缓冲半径的增大，填平或缩小的趋势逐渐变大，上缓冲面的凸地形区域形态虽然受到周围地形的影响发生变化，但仍然保持凸部形态；③下缓冲面的凸地形区域均有被削平或缩小的趋势，且随着缓冲半径的增大，削平或缩小的趋势逐渐变大，下缓冲面的凹地形区域形态虽然受到周围地形的影响发生变化，但仍然保持凹部形态；④由等深线图可以看出，由于TIN_DDM上缓冲面“填凹保凸”和下缓冲面“削凸保凹”的特性，TIN_DDM缓冲面均逐渐趋于平坦，且各自然邻点间的z坐标值变化幅度随滚动球半径的增大而减小。

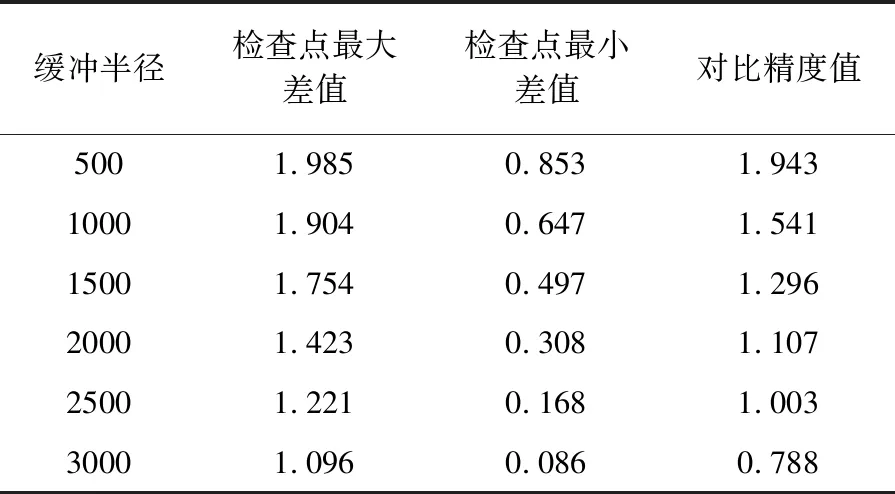
此外，为验证本文方法在模型精度保持上的优势，以文献[12]所提算法构建矢量缓冲面作为参考，借鉴TIN_DDM精度评估最常用的逐点检查法来对3种算法所构建缓冲面的精度进行对比分析，将检查点按照50×50的网格进行分布，其中水深数据的测量中误差σ为1 m，TIN_DDM平面Delaunay三角网中各自然邻点间的最大间距值dmax为31.2 m。对文献[12]所提算法和算法Ⅰ、Ⅱ(算法Ⅰ、Ⅱ试验结果相同)所构建的上缓冲面进行精度对比统计分析，试验结果如表2所示。

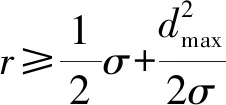
表2 文献[12]所提算法与算法Ⅰ、Ⅱ所构建缓冲面精度对比统计

Tab.2 The comparing accuracy of the buffer surface constructed by the reference [12] and algorithm Ⅰ or Ⅱm

缓冲半径检查点最大差值检查点最小差值对比精度值5001.9850.8531.94310001.9040.6471.54115001.7540.4971.29620001.4230.3081.10725001.2210.1681.00330001.0960.0860.788

最后，为体现本文所提面向TIN_DDM缓冲面构建的滚动球加速优化模型的效率优势，选取同一海区水深采样点密度相差不大的3块TIN_DDM进行试验。试验1的水深点数为12 477，试验2的水深点数为18 825，试验3的水深点数为25 042。对算法Ⅰ、Ⅱ的耗时情况分别进行统计分析，结果如图6所示。此外，本文还尝试利用文献[12]所提算法构建TIN_DDM矢量缓冲面，但由于三维空间求交运算消耗内存较大，当前试验环境已不支持整体TIN_DDM矢量缓冲面构建及三维显示。此处选取缓冲半径为500 m，选取试验1中70个水深采样点进行矢量缓冲面构建，其算法耗时为204 s。对于其中单个水深采样点的等距离球面与其余等距离球面的求交运算时间平均为2.91 s。预估其整体TIN_DDM矢量缓冲面构建时间为36 308 s，已远远超过算法Ⅰ和算法Ⅱ最大缓冲半径时的缓冲面构建时间，且随着缓冲半径的增大，参与各点等距离球面求交运算的其余等距离球面将更多，算法运行时间将更大。

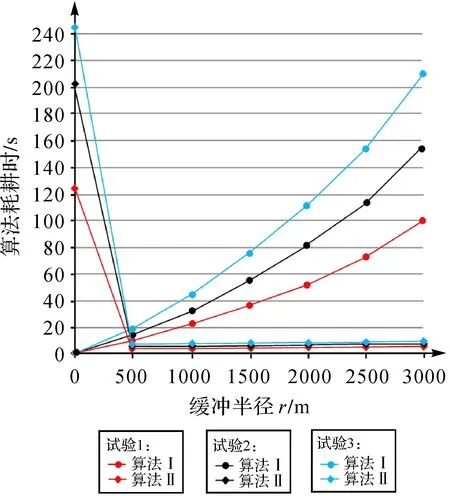
图6 各算法耗时统计图Fig.6 The time loss of each algorithm

试验结果表明：①本文所提算法Ⅱ前期需要进行数据预处理，主要建立TIN_DDM缓冲面构建关键采样点与滚动球半径之间的数值关联性数据链，以实现对滚动球模型的加速优化，而算法Ⅰ无须进行前期预处理；②在同一TIN_DDM内不同缓冲半径下的缓冲面构建过程中，算法Ⅰ将滚动球模型应用扩展至TIN_DDM缓冲面构建中，采用单值曲面逻辑并运算法则代替大量的几何求交运算，大大缩短算法耗时，将时间复杂度降至O(nr2)，而算法Ⅱ在算法Ⅰ的基础上进行改进，通过TIN_DDM缓冲面构建关键采样点与滚动球半径之间的数值关联性数据链，对面向TIN_DDM缓冲面构建的滚动球模型进行加速优化，将后期应用的时间复杂度降至O(n)；③随着缓冲半径的增大，算法Ⅰ的耗时逐渐增大，主要是由于随着滚动球半径的增大，参与各采样点z轴方向上极值点确定的等距离球面逐渐增多，导致算法耗时增加，而算法Ⅱ后期主要通过简单的数据查询方式确定TIN_DDM缓冲面构建关键采样点，其算法耗时受缓冲半径变化的影响较小，且各缓冲半径的上下缓冲面构建时间相差不大；④在不同TIN_DDM内，算法Ⅰ的时间复杂度为O(nr2)，在同一缓冲半径的条件下，其算法耗时与TIN_DDM的点数成正比关系，而对于算法Ⅱ，其前期预处理过程耗时与TIN_DDM数据点数和各水深采样点所对应的TIN_DDM缓冲面构建关键采样点个数均具有直接关系，则其算法前期预处理耗时与TIN_DDM的点数呈正相关关系，在后期应用过程中，算法通过数据查询方式确定TIN_DDM缓冲面构建关键采样点，其后期算法耗时与TIN_DDM的点数成正比关系。

4 结 论

本文在分析借鉴基于滚动球模型的单值曲面缓冲体边界生成算法的基础上，通过将滚动球模型引入至TIN_DDM缓冲面的构建过程，提出了一种基于滚动球加速优化模型的TIN_DDM缓冲面快速构建算法。首先，针对滚动球模型在TIN_DDM缓冲面构建过程中存在的精度应用局限，分析论证了影响滚动球模型精度的关键误差累积规律，并以滚动球半径为关键阈值，建立了滚动球整体精度的定量评估与控制模型；其次，针对大数据量TIN_DDM缓冲面多次构建的应用效率需求，阐明了关键采样点与滚动球半径对TIN_DDM缓冲面构建效率的影响机理，建立了关键采样点的判定准则及与滚动球半径的数值关联关系，构建了面向TIN_DDM缓冲面构建的滚动球加速优化模型；最后，结合试验分析对本文模型与算法进行了精度与效率的验证。试验结果表明，本文算法可有效控制TIN_DDM缓冲面的构建误差，且可在一次数据预处理的前提下，实现大数据量TIN_DDM缓冲面的多次快速构建。需要指出的是，本文方法主要针对单值曲面这类特殊形态的地理要素，通用性不强，且在算法解算过程中，并未涉及TIN_DDM数据分块索引的建立与管理，难以实现模型的并行运算与处理。下一步将尝试利用所提算法构建非单值曲面缓冲体边界，并进一步研究如何根据实际TIN_DDM水深采样点分布情况进行数据的自适应分块及算法的并行运算等问题。