对全要素生产率的讨论:数据启示
2019-06-06
(西南科技大学 四川 绵阳 621000)
改革开放以来,我国经济持续高速增长,成为国内外众多学者关注和研究的焦点。保罗·库格曼(1949)认为“东亚奇迹的神话”是不可持续的,东亚增长模式的争论引起了人们特别是东亚国家和地区对经济增长质量—全要素生产率的研究与探讨[1]。本文总结了国内外测算全要素生产率方法,对主要的研究范围作了归纳。基于柯布-道格拉斯生产理论测算中国的全要素生产率,从而对TFP的变化情况进行检验和探讨。
一、全要素生产率定义
全要素生产率是指资本和劳动投入之外的教育、创新、规模效益、科学进步等导致的产出增加,是剔除要素投入贡献后所得到的残差,最早由索洛(Solow,1957)提出,故也称为索洛残差[2]。由于引起经济增长的因素繁多,于是引入资本和劳动之外的TFP来衡量其他要素引起的经济增长。
二、测度方法评述
(一)索洛残差法(SR)
Solow提出全要素生产率表示为产出经济增长率扣除劳动和资本贡献之后的余额。
基础模型:Y=A(t)LαKβ
优点:索洛残差法开创了经济增长源泉分析的先河,是新古典增长理论的一个重要贡献(Lucas,1988)。
缺陷:索洛残差法建立在新古典假设即完全竞争、规模收益不变和希克斯中性技术基础上,这些约束条件难以满足;索洛残差法用所谓的“残差”来度量全要素生产率,无法剔除掉测算误差的影响。
采用索洛残差法的文献:沈坤荣(1997)确定资本产出弹性为0.4,劳动产出弹性为0.6,以此进行经济增长因素分析和全要素生产率的测算;李京文、钟学义(1998)估算出我国1953-1955年间全要素生产率变动情况;WangandYao(2003)假设劳动产出弹性和资本产出弹性都为0.5,以此来分析中国1953-1999年间经济增长[3]。
(二)隐性变量法(LV)
隐性变量法将TFP看做一个不可观测的变量,在检验数据平稳性和协整性的基础上,利用状态空间模型做极大似然估计来估算。
基础模型:
ΔLn(Yt)=ΔLn(TFPt)+αΔLn(Kt)+(1-α)ΔLn(Lt)+εt
优点:将TFP看做一个独立的状态变量并从残差中分离出来,更为精确地估算了全要素生产率。
缺陷:仍建立在新古典基础上,仍然采用规模报酬不变假定和C-D生产函数形式。[4]
(三)随机前沿生产函数法(SFA)
Fare等认为经济增长来源于投入要素增长、技术进步和技术效率提高,把全要素生产率增长率分解为技术进步率和技术效率两部分。技术进步率是较长期内测算技术效率的参照物,前沿生产函数正是测度这个参照物的有用工具。
基础模型:
Y=f(K,L)ev-u
其中v表示随机误差,服从均值为0、方差不变的正态分布,而u服从半正态分布、截尾正态分布或者指数分布。根据前沿生产函数的不同,分为两类:超越对数生产函数和CD生产函数[5]。
优势:不再将全要素生产率视为残差,而是将其视为一个独立的状态变量,将全要素生产率从残差中分离,从而剔除掉一些测算误差对估算的影响。同时,充分考虑了数据非平稳性带来的伪回归问题。
缺陷:该模型建立在产出缺口估算基础上,而无论用何种方法估算产出缺口,都会存在估算误差。
采用随机前沿生产法的文献:姚洋(1998)对第三次工业普查的抽样数据做截面分析的研究;涂正革、肖耿(2005)对中国工业生产力发展趋势及潜力的研究;王争、郑京海(2006)对中国工业生产效率的地区差异的研究。
(四)代数指数法(AIN)
最早由艾布拉姆威兹(Abramvitz,1956)提出,基本思想是把TFP表示为产出数量指数与所有投入要素加权指数的比率。
P0Qt=TFPt(r0k0+W0Lt)
其中,r0、W0和P分别为基期利率、工资和价格。
优点:直观地体现出全要素生产率的内涵。
缺陷:若没有明确设定生产函数,就不能把全要素生产率指数进行再分解,运用较少[6]。
(五)数据包络分析法(DEA)
Charnes和Cooper等在1978年提出DEA理论,将DEA方法和Malmquist指数构造方法联系起来,该种方法首先从投入的角度或者产出的角度利用DEA方法定义距离函数,然后在距离函数的基础上构造Malmquist指数用来度量生产率。
基础模型:
x表示投入,y表示产出。
优点:不需要考虑投入和产出的生产函数形态,可以研究多投入和多产出的全要素问题,DEA模型中投入产出变量的权重由数学规划模型根据数据产生,不受人为主观因素的影响。
缺陷:该模型容易受到随机因素的影响;该方法所得到的技术进步增长率和技术效率增长率的变化方向往往是相反的;由于Malmquist生产率指数的构造可以从投入角度、产出角度两个角度出发,出发角度的不同导致计算得到的结果不同。
采用数据包络分析法的文献:颜鹏飞、王兵(2004)测度了1978-2001年中国30个省份全要素生产率增长情况;孟令杰、李静(2004)对1952-1998年间的全要素生产率增长情况作了测算;岳书敬、刘朝明(2006)考察了1996-2003年间全要素生产率增长、技术进步以及技术效率变动情况。
三、主要研究方向分类
(一)针对经济增长的研究
李京文(1993)首次对我国的生产率和经济增长问题进行了全面系统的分析;张军和施少华(2003)估计了1952至1998年我国全要素生产率增长率,发现改革前我国全要素生产率波动很大,改革后有明显提高,1978至1998年平均增长率约为2.8%,生产率的提高贡献了产出增长中的28.9%[7];易纲、樊纲、李岩(2003)分别从制度变迁、人力资本素质提高等方面证明了中国经济增长效率提高,他们认为新兴经济国家由于与发达国家的投资方向不同,导致其技术进步机理也不同,因此全要素生产率的测算方法也应有所区别[8];郑京海、胡鞍钢(2005)研究发现1978至1995年的中国TFP平均增长率为4.6%,而在19%至2001年出现低增长0.6%,指出全要素生产率变化呈现技术进步速度减缓、技术效率有所下降的特点[9]。
(二)针对具体产业的研究
谢千里等人(1994)测算了1980至1992年我国工业生产率的趋势,发现1988至1992年工业生产率增速减缓,主要原因是设备利用率下降和国企改革的选择性差异以及国有工业的资本收益率下降;孟令杰(2002)用非参数的Malmquist生产率指数方法,分析了1980-1995年间我国农业TFP的增长及增长率的构成因素;李静等(2006),研究发现改革开放以来我国农业全要素生产率的增长主要是由技术进步推动的,技术效率的下降对TFP增长造成了不利影响,而规模效应和混合效应的影响较弱[10]。
(三)针对特定领域的研究
国外研究的重点偏向于R&D(科学研究与试验发展)与TFP的关系。Gary Madden(2001)以亚洲和OECD国际R&D溢出为研究对象,建立一个将TFP与国内外R&D活动联系起来的经验模型;同时,TFP的收敛分析在国外受到了一些学者的关注,如MillerandUpadhyay(2002)进行了国家间收入和TFP收敛的对比研究,研究结果表明,收入的收敛和TFP的收敛既有相似的地方,也有不同之处。
国内方面,彭国华(2007)研究了人力资本构成与地区全要素生产率的关系;李培(2007)利用DEA对中国城市的效率与差异进行研究。
四、我国全要素生产率的测算
(一)方法与模型
假设中国经济的生产函数为:
Y=A(t)L
(1)
其中以α和β分别代表劳动和资本的产出弹性,根据经验估计方法,劳动力产出弹性取0.4,资本产出弹性取0.6[12]。则全要素生产率等于:
TFP=A(t)=Y/LαKβ
(2)
(二)数据说明
本文选取国内生产总值、就业人数、全社会固定资产投资分别作为产出、劳动投入和资本投入的衡量指标,数据均来自中国统计局官网,具体数据参见图1
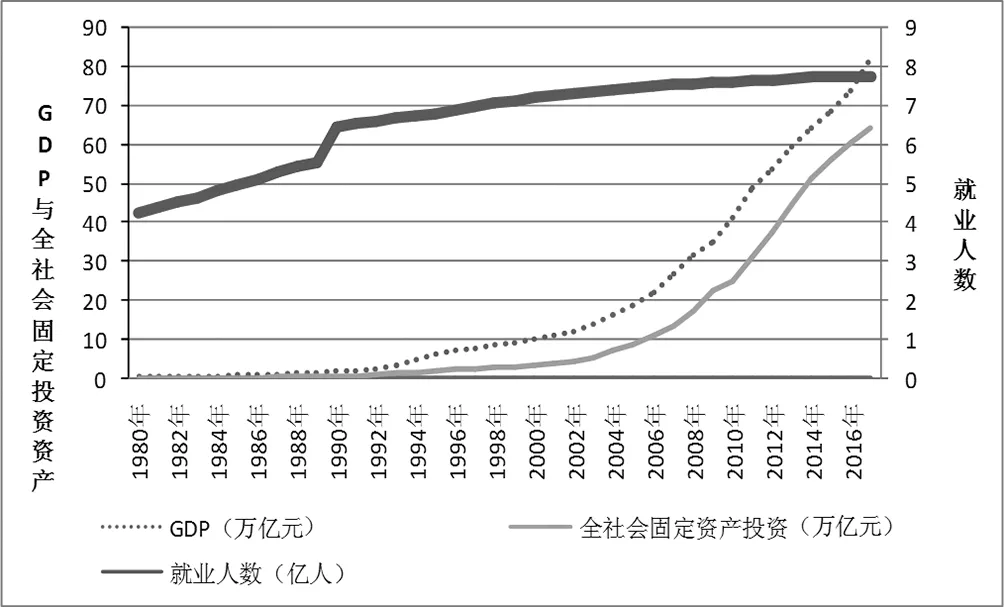
图1 1980年-2017年中国经济数据
(三)结果及分析
由图2可以看出,在1980年-2017年这段时间内,随着资本的增长额不断增加,劳动的增长额不断减少,中国的TFP总体上呈现一个上升趋势,而TFP增长率则呈现涨跌互现的波动情形,且波动较为频繁。
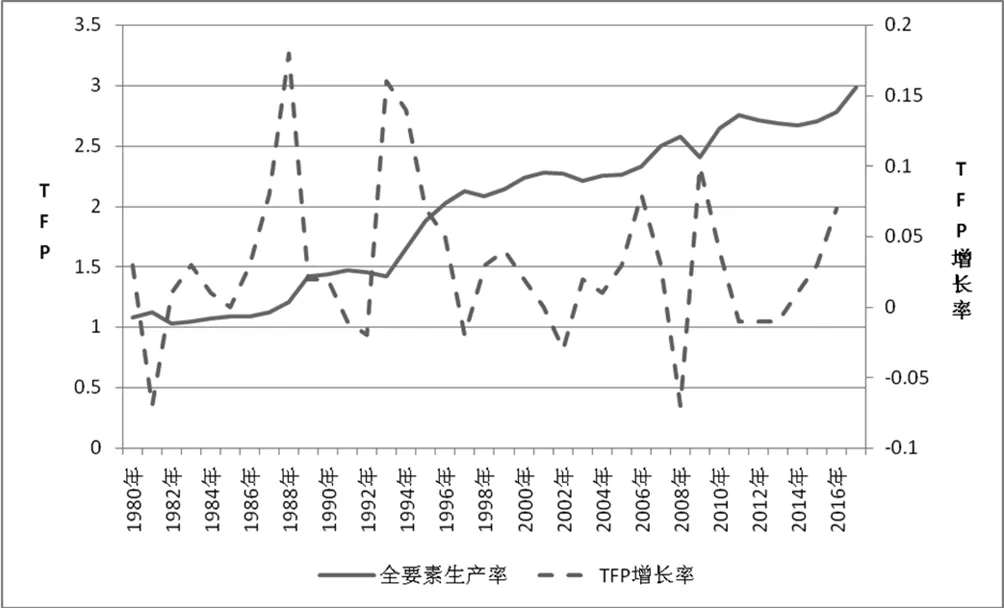
图2 全要素生产率及其增长率
结语
本文整理出五种计算全要素生产率的方法,并对其进行评述。利用Cobb-Douglas生产函数,对中国1980-2017年的TFP进行了估算。由于相关数据的缺乏,本文在指标的选取上存在一定局限性,可能导致结果出现偏差;其次,没有对全要素生产率和经济增长之间的关系做进一步探讨。
