选图题的“秒杀”策略
2019-06-06付胜亮
付胜亮
(山东省临沂第十八中学 276017)
一、特值优先——绝招
特值策略是处理函数图象类问题的“绝招”, 应用这种策略时应抓住函数解析式的特征,灵活选取函数图象上的某些特殊点,加以对照,逐一排除,可迅速得到答案.
例1函数y=xcosx+sinx的图象大致为( ).
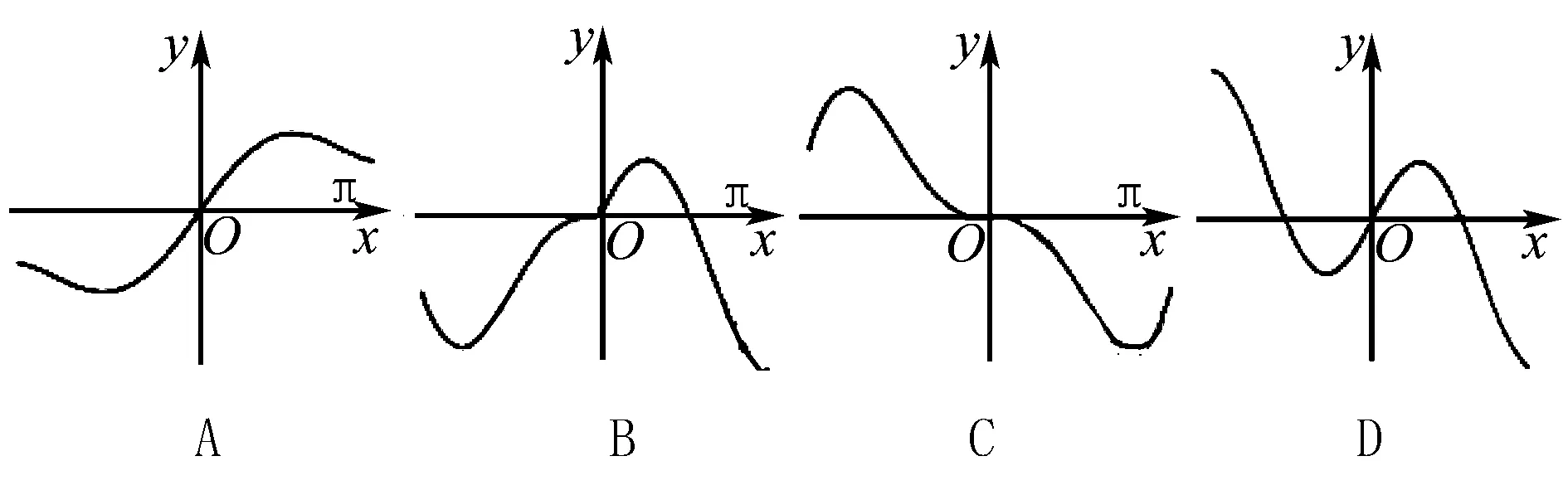
解析当x=π时,y=-π<0,排除A;

当x=-π时,f(-π)=π>0,排除B.选D.
评析选取函数图象中的特殊点时,还应结合基本函数的性质,根据某些性质对函数图象作出判断.如本题可由函数为奇函数排除B.
二、函数性质——基础
熟练掌握函数的基本性质如:定义域、值域、奇偶性、单调性、周期性、对称性等,是解决函数图象问题的基础.对于给出函数解析式,判断其大致图象的问题,应优先考虑函数的基本性质.


解析由函数为偶函数,图象关于y轴对称,排除B、D;又cosx∈(0,1),所以y<0,排除C.选A.
评析本题利用函数的奇偶性初步作出判断,然后利用函数的值域得出结论.这种利用函数的多个性质,综合分析判断是解决函数图象问题的最基本的方法.
三、极限分析——辅助
当选取函数图象上的特殊点以及结合函数的性质不能解决问题时,往往选取函数图象中的极限点,如x→0、x→+∞等,结合解析式得出函数图象的变化趋势,得到结论.
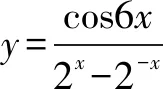

解析因为函数为奇函数,所以图象关于原点对称,排除A;当x趋向于+∞时,2x-2-x趋向于+∞,cos6x∈[-1,1],所以y趋向于0,排除C;当x从正方向趋向于0时,2x-2-x>0,cos6x>0,排除B.选D.
评析极限分析法往往是用无限趋近的思想,结合单调性、有界性、最值等作出判断.
四、导数定性——精准
导数是研究函数的有力工具,利用导数可迅速地判断出函数的单调性、极值以及图象变化快慢程度,更精准地判断图象,从而迅速得出答案.
例4 函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为( ).


f′(x)=cosx-cos2x=-2cos2x+cosx+1=-(cosx-1)(2cosx+1).
f′(x)>0⟺-(cosx-1)(2cosx+1)>0


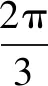
评析本题利用特殊点及函数的性质不能得出答案,需借助导数判断极值点的位置方可.
五、图象变换——简化
熟练掌握基本初等函数的图象,以及平移、对称、伸缩、翻折、周期等图象变换的方法和技巧,能快速地解决图象变换类问题.
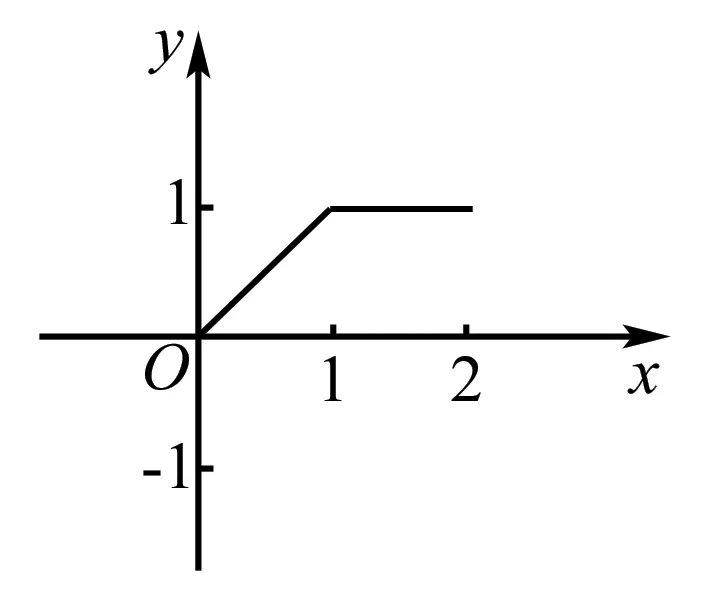
例5 已知定义在区间[0,2]上的函数y=f(x)的图象如图所示,则y=f(2-x)的图象为( ).

解析y=f(2-x)的图象是由函数y=f(x)的图象先按照关于原点对称得到,然后将函数的图象向右平移2个单位即可,选B.
评析熟练掌握基本函数的图象及几种常见的图象变换是解决好本题的关键.本题也可用特殊值解决.
六、趋势变化——直觉
例6 小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶. 与以上事件吻合得最好的图象是( ).

解析开始时匀速行驶,此时对应的图象为直线,函数的图象递减.途中因交通堵塞停留了一段时间,此时到学校的距离为常数,加速行驶时对应的图象为直线,但要比开始时陡一些.选C.
评析本题需理解横纵坐标的含义,结合实际意义分析出函数的图象是直线,理解图象的变化情况是解题的关键.
七、函数导数对照——热点
由导函数的图象得出原函数图象的大致变化情况,或由原函数的图象得到导函数的图象,是高考的重点和热点问题.由导数值的正负确定原函数的单调性,由导函数的零点确定原函数的极(最)值,由导数值的大小变化情况确定原函数的变化快慢情况,是解决这类问题的依据.

例7 已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是( ).

解析由导函数图象可知函数的函数值在[-1,1]上大于零,所以原函数递增,且导函数值在[-1,0]递增,即原函数在[-1,0]上切线的斜率递增;导函数的函数值在[0,1]递减,即原函数在[0,1]上切线的斜率递减.选B.

例8如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( ).

解析最初零时刻和最后终点时刻面积没有变化,导数取零,排除C;露出水面部分的面积一直保持增加,没有负的改变量,排除B;考察A、D的差异在于两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断.选A.
评析导数的几何意义是曲线的切线的斜率,是解决这类问题的根本.
上述这些方法并不是孤立使用的,在解决问题时,可以相互交叉,灵活应用.
