幼儿心理数线的发展：估计准确率与模式背后的策略 *

臧蓓蕾 张 俊 顾荣芳

(南京师范大学教育科学学院，南京 210097)

1 引言

心理数线（mental number line）是对数字在大脑中表征的比喻，是数量表征的一种形式（Dehaene, Bossini, & Giraux, 1993）。已有关于心理数线的研究主要采用数线任务（number-line task）进行探究（Link, Huber, Nuerk, & Moeller,2014; Simms, Clayton, Cragg, Gilmore, & Johnson,2016）。目前使用数线任务研究心理数线主要有两个发现：第一是儿童的年龄越大，数线估计的正确率越高；第二是儿童的表现反映了表征模式的变化，年幼儿童会高估小数字，低估大数字，表现出对数模型。随着儿童年龄的增长，儿童会逐渐更加平均地分配数字，表现出线性的模型（Booth & Siegler, 2006; Siegler & Booth, 2004）。对数模型是指位于数字线较小一端的数字比较大一端的数字拥有更大的心理距离，实际数值大小与心理数值大小是以对数关系对应的；线性模型则是指实际数值大小与心理数值大小是线性对应的，数字的心理距离和理论距离是线性相关的（刘国芳, 辛自强, 2012）。已有研究大多认为儿童会逐渐从对数估计模型转换到线性估计模型（ Booth & Siegler, 2006; Siegler & Opfer, 2003），然而近年来越来越多的研究者对此提出质疑，指出双线性、多线性等其它估计模型的存在（Bouwmeester & Verkoeijen, 2012; Ebersbach, Luwel, Frick,Onghena, & Verschaffel, 2008; Slusser, Santiago, &Barth, 2013）。

有研究者意识到数线估计模型差异背后的意义，转而在纷繁复杂的模型之争背后寻找可能的差异根源。Siegler 和Opfer（2003）在研究中发现估计的准确率与数量的大小相关，儿童会使用数字的分界点对数线进行划分，由此认为儿童可能会运用一定的策略进行数线估计。国内也有学者对5～6 岁幼儿在0～100 数线范围内的估计能力、工作记忆能力对数线估计结果的影响进行了研究，结果发现幼儿是一个“灵活的策略使用者”，倾向于使用中点和端点策略进行数线估计（刘国芳, 辛自强, 2012）。作为一种复杂的认知过程，数线估计需要幼儿多方面认知能力的参与。已有研究认为幼儿数量估计的策略包括眼球效应、基准比较等策略（Crites, 1992），然而幼儿数线估计与数量估计又有所不同。幼儿究竟是如何进行数线估计的，是否可能会表现出相关的估计策略？如果具有估计策略，它们与数线估计的准确率、估计模型是否有联系？

首先，已有关于心理数线研究的对象多为西方国家5～6 岁及以上年龄阶段的儿童和成人，数线估计范围为0～100 或0～1000（Opfer, Thompson,& Kim, 2016; Slusser et al., 2013）。极少有研究向另一端延伸，即探究更小的年龄阶段和更小的数线估计范围（1～5/1～10/1～20）中心理数线的发展特点（Ramani & Siegler, 2008; Siegler & Ramani,2008），以了解儿童在早期对数量表征及数量关系的认知特点。国内关于心理数线的研究并不多，特别是幼儿心理数线发展的研究更少。心理数线是数概念发展的重要组成部分，与各种数学能力的发展密切相关（Schneider, Grabner, & Paetsch,2009）。由于文化传统等各方面因素的影响，中国幼儿的数量表征能力发展水平高于西方同龄幼儿（Laski & Yu, 2014; Siegler & Mu, 2008），因此有必要对学前期幼儿的心理数线发展特点进行探究。

其次，已有研究的数线估计任务情景都较为单一，即只采用相同数线跨度的一种估计情景，极少有研究对不同的情景进行对比（Laski & Yu,2014; Xu, Chen, Pan, & Li, 2013）。再次，在以往关于心理数线的研究中，大多数研究只对参与者的数线估计结果进行量化的分析，而缺少对参与者的数线估计过程进行关注。已有关于儿童心理数线的研究多为估计准确率和估计模式的研究，极少有对儿童数线估计策略的研究，也并未有对更小年龄的幼儿在更小的数线估计范围内的估计策略的探究。

由于3～5 岁幼儿具有动作思维的认知发展特点，幼儿在完成数线估计任务的过程中可能会有外显的策略表现情形。因此本研究首先将对3～5 岁幼儿在两种不同估计情景中的三个不同数线范围（1～5/10/20）心理数线的发展特点进行探究，并在幼儿完成数线估计任务的基础上，通过对幼儿策略使用情况的观察以及与幼儿对话询问的方式分析不同年龄阶段幼儿在不同估计情景中进行数线估计所使用的策略，初步探究幼儿在数线估计任务中的策略使用情况及策略使用与幼儿心理数线发展水平之间的关系，从而更加深入立体地了解幼儿心理数线的发展特点。

2 研究方法

2.1 研究对象

研究者在N 市两所普通公办幼儿园分别选取小班幼儿41 名（平均月龄51 个月），中班幼儿40 名（平均月龄63 个月），共81 名幼儿参与心理数线估计策略的研究，具体见表1。

表 1 参与研究儿童人数及平均月龄分布表

2.2 研究工具

本研究采用Siegler 和Booth 等已有研究中采用的NP（number-to-position, 数字到位置）数线估计任务（Siegler & Booth, 2004; Siegler & Mu, 2008;Simms, Muldoon, & Towse, 2013），已有研究中使用数线估计任务的研究对象多为6 岁以上的儿童，数线估计任务中的数线范围为0～100。研究者结合研究目的，考虑到3～5 岁幼儿数概念及认知发展水平，对数线估计任务的范围和操作形式进行了调整，将数线范围调整为0～5/10/20，操作形式更加游戏化，以便于幼儿理解和操作。

测查材料为一张印有数线的1/4 大小的A4 纸（长为297 mm, 宽为52.5 mm）操作单，数线左边为数字1，右边为数字X（X=5/10/20），数线中间上方20 mm 处有一个待估计数字N（1＜N＜X）。

测查材料分为两组，第一组（情景一）测查材料为跨度相同（171 mm），数距不同的数线估计任务单，即1～10 和1～20 的数线长为171 mm，1～5 的数线长为172 mm（为便于精确测量和计算,故取172 mm, 数距长度为43 mm）。

第二组（情景二）测查材料为跨度不同，数距相同（9 mm）的数线估计任务单，即1～5 数线长为36 mm，1～10 的数线长为81 mm，1～20 的数线长为171 mm，数距都为9 mm。第一组（情景一）测查材料1～20 数线范围的操作单与第二组（情景二）测查材料1～20 数线范围的操作单相同，数线长为171 mm，数距为9 mm。每组包括1～5、1～10、1～20 三个数线范围的共17 张测查单。

被估计数字的选择主要有以下两个方面的考虑，一方面根据中班、小班幼儿的实际情况，测查时间不宜过长，因而数线范围内的每个数字不可能都被测查；另一方面，研究者参考已有研究测查任务中选择的被估计数字。因而1～5 数线要估计的目标数字为：2、3、4（共3 个）；1～10数线要估计的目标数字为：2、3、4、6、7、8、9（共7 个）；1～20 数线要估计的目标数字为：3、4、6、8、12、14、17（共7 个）。

每个估计的数字都是在一张单独的操作单上，每个数线范围内需要估计的数字是随机的顺序。40 名幼儿参与情景一的测查，41 名幼儿参与情景二的测查。

2.3 研究步骤

研究者首先对幼儿进行数线估计任务的测查，在每一次测查前，主试都会口头提醒以下指导语：“数字宝宝1 到5/10/20 排在这条线上，这边是数字宝宝1，这边是数字宝宝5/10/20，数字宝宝N 回来了，你觉得它应该排在哪里?”测查后，研究者对每位幼儿在三个不同数线范围内都进行了策略的询问：“你是怎么知道的?”在幼儿操作过程中，研究者观察并记录了每一位幼儿的数线估计过程和策略。

测查之后，研究者一方面对测查结果进行量化统计分析，确定幼儿数线估计准确率及估计模式；另一方面，研究者根据测查时对幼儿回答的记录及后期视频的回放和观看，将幼儿表述策略的话语进行记录和整理，并对这些话语进行编码和分类。研究者试图通过对策略的记录和分析，在量化的数据结果和质性的策略记录中寻找可能的对接点，探究幼儿心理数线的发展与其策略使用之间的相关性。

3 结果与分析

3.1 数线估计策略特点

研究者通过对策略的梳理和编码，发现幼儿一共表现出六种不同的数线估计策略，分别为：“不知道”、“其它”、“视觉线索”、“数数”、“参照端点”、“数字关系”，其中后四种为有效的估计策略。

“不知道”是指幼儿不进行回答或者直接回答“不知道”、“不清楚”；“其它”策略是指幼儿回答“猜的”、“就是知道”等策略，或者回答的“策略”与数线估计任务不相关，例如幼儿回答“画瓢虫知道的”，“永远超级知道”等；“视觉线索”策略是指幼儿通过观察数线完成数线估计任务，或者回答“我看出来的”，“刚才看到的”等；“数数”策略是指幼儿回答和数数相关的策略，例如幼儿回答“因为1、2、3、4、6”，“会数数知道的”等等，或者幼儿表现出数数（包括默数）的行为；“参照端点”策略是指幼儿参照数线两端的数字，例如幼儿回答“看20 在这里，8 应该离20 远一点”，“看10 在这里”，“因为20 后面有数字，14 就该在这里”；“数字关系”是指幼儿运用数字之间的关系进行推断，例如幼儿回答“7 在8 的旁边”，“3 在中间，2 在这边”，“因为9 是在8 的后面”。各年龄阶段幼儿在不同情景和数线范围的数线估计任务中使用的策略种类频数及百分比具体见表2。

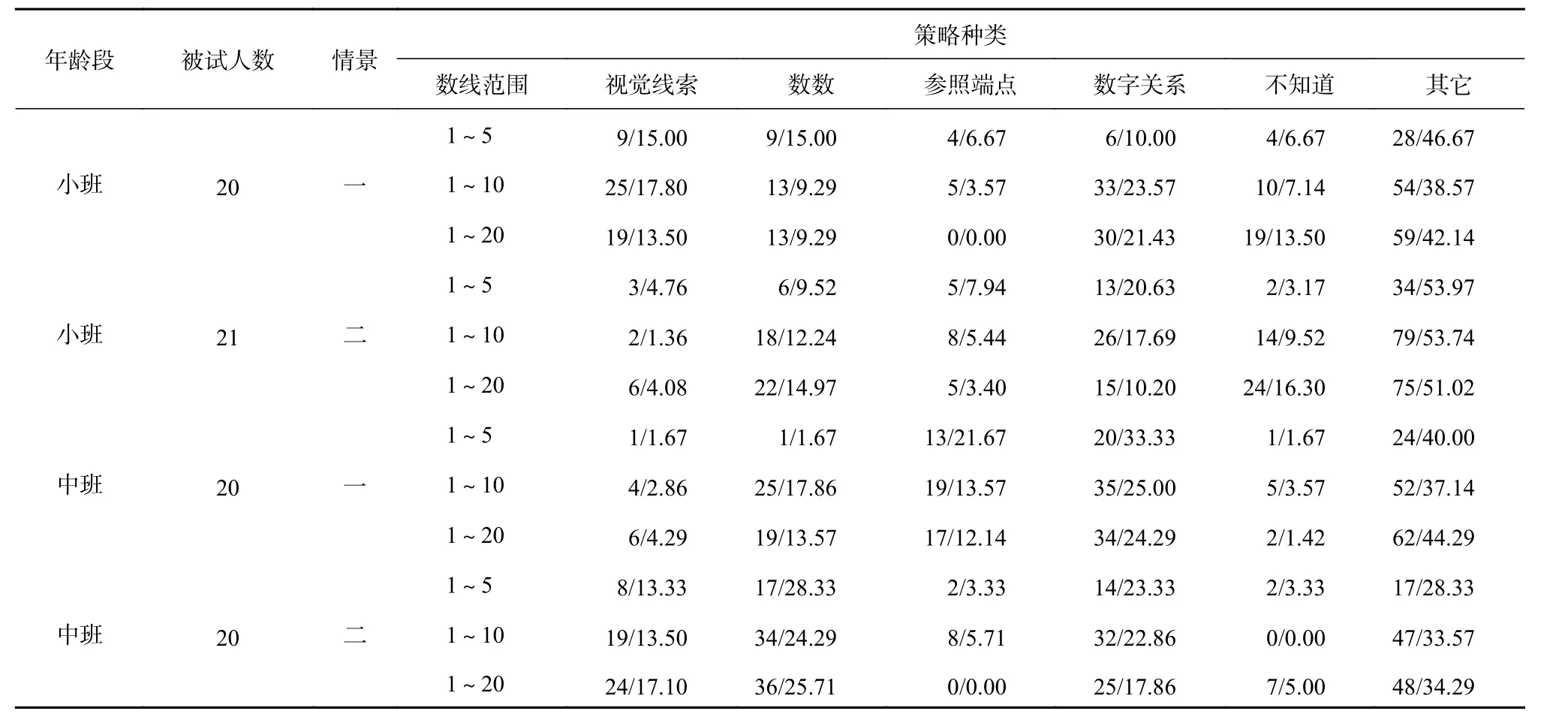
表 2 幼儿数线估计策略频数及百分比

综合各个数线范围内不同年龄阶段幼儿在不同数线估计情景中使用策略差异的分析结果，可以发现：与中班幼儿相比，小班幼儿较多使用“不知道”策略，比例随着数线范围的扩大而增长，尤其在1～20 数线范围内的两种不同情景中，小班幼儿使用此策略显著多于中班幼儿（χ2=13.76, df=1, p＜0.01, Φ=0.81; χ2=9.32, df=1, p＜0.01,Φ=0.55）；幼儿在三个数线范围内对“其它”策略使用频率都较高，小班幼儿在情景二的三个数线范围内对此策略的使用频率显著高于中班幼儿（χ2=5.67, df=1, p＜0.05, Φ=0.33; χ2=8.13, df=1, p＜0.01,Φ=0.26; χ2=5.93, df=1, p＜0.05, Φ=0.22）；在三个不同数线范围内，小班幼儿在情景一中使用“视觉线索”策略的频率显著高于情景二，而中班幼儿在情景二中使用此策略的频率较高；关于“数数”策略，幼儿在情景二的使用频率显著高于情景一，中班幼儿使用频率显著高于小班幼儿（χ2=13.19, df=1, p＜0.01, Φ=0.25; χ2=12.21, df=1, p＜0.01,Φ=0.24）；幼儿使用“参照端点”策略在1～5 数线范围内比例最高，随着数线范围的扩大而逐渐降低，中班幼儿在不同数线范围内情景一的使用频率显著高于情景二（χ2=8.07, df=1, p＜0.01, Φ=0.73;χ2=4.48, df=1, p＜0.05, Φ=0.41）；关于“数字关系”策略，中班幼儿在各情景中普遍多于小班幼儿，“数字关系”在1～10 数线范围内比例最高。

总体看来，按照使用的频数及百分比，从高到低的次序依次为：“其它”、“数字关系”、“数数”、“视觉线索”、“参照端点”、“不知道”。小班幼儿较多使用的是“不知道”和“其它”的策略，而中班幼儿使用有效策略的频率显著提高。

3.2 主要数线估计策略与绝对误差百分比

为了解幼儿数线估计策略与其估计准确度之间的关系，研究者对每位幼儿在各个数线范围内的估计策略进行归纳，以每位幼儿在测查中使用频率最高的策略为准，确定每位幼儿在某一数线范围内的主要估计策略。采用单因素方差分析，了解不同数线范围内每位幼儿的绝对误差百分比（percent absolute error，PAE）均值与其主要估计策略是否存在差异。在本研究中，绝对误差百分比为：|（估计的数的长度—被估计的数的长度）/数线总长度|。绝对误差百分比越低，表明估计的准确率越高。方差分析结果表明：在1～5 数线范围内，幼儿估计的绝对误差百分比不存在显著的策略差异，F（5, 75）=0.77，η2=0.05，p＞0.05；在1～10 数线范围内，幼儿估计的绝对误差百分比不存在显著的策略差异，F（5, 75）=0.35，η2=0.02，p＞0.05；在1～20 数线范围内，幼儿估计的绝对误差百分比存在显著的策略差异，F（5,75）=3.30，η2=0.18，p＜0.05。事后分析的多重比较结果显示，“不知道”策略和其它五种策略（“视觉线索”、“数数”、“参照端点”、“数字关系”、“其它”）的绝对误差百分比差异显著，p＜0.05；“其它”策略和“数数”策略的绝对误差百分比差异显著，p＜0.05。具体见表3。

3.3 主要数线估计策略与数线估计模式

研究者通过对幼儿数线估计任务数据结果的统计分析，借助Mplus7.0 软件进行潜在类别分析（latent class analysis），确定每位幼儿的心理数线估计模式。潜在剖面分析（latent profile analysis）是潜在类别分析的一类，具有连续潜在类别指标的潜在类别分析常被称为潜在剖面分析。在潜在剖面分析中，阿凯克信息准则（AIC）、贝叶斯信息准则（BIC）、贝叶斯准则校正指标（ABIC）数值越低，信息熵Entropy（取值介于0～1）越高表示模型的拟合度越高。此外，LMR（lo-mendellrubin likelihood ratio test, 罗梦戴尔鲁本校似然比）和BLRT（bootstrapped likelihood ratio test,Bootstrapped 似然比检验）能够辅助比较和判断最佳类别模型，如果LMR 和BLRT 指标的p 值达到显著性水平，则表示K 个类别的优于K-1 个类别（Muthén & Muthén, 2012）。

从表4、表5 和表6 可以看出，AIC、BIC 值随着分类数量的增加而不断下降，较低的AIC、BIC 值，较高的Entropy 值和显著的LMR 和BLRT预示着模型的拟合度较好。综合上述指标，幼儿在1～5 数线范围中4 个类别模型的LMP p 值显著（p＜0.05），表明4 个类别的模型优于3 个类别的模型，且4 个类别模型的Entropy 指标最高，因此选择4 个潜在类别的分类；在1～10 数线范围中各个类别模型的LMP p 值都不显著，但是3 个类别的Entropy 指标最高，因此选择3 个潜在类别的分类；在1～20 数线范围中各个类别模型的LMP p 值都不显著，但是2 个类别的Entropy 指标最高，因此选择2 个潜在类别的分类。根据选定的潜在类别分类，在Mplus 中导出潜在剖面图，坐标调整后的不同数线范围各个类别的LCA 剖面图见图1。

表 4 幼儿1 ～ 5 数线范围的潜在剖面（LPA）的各项指标比较

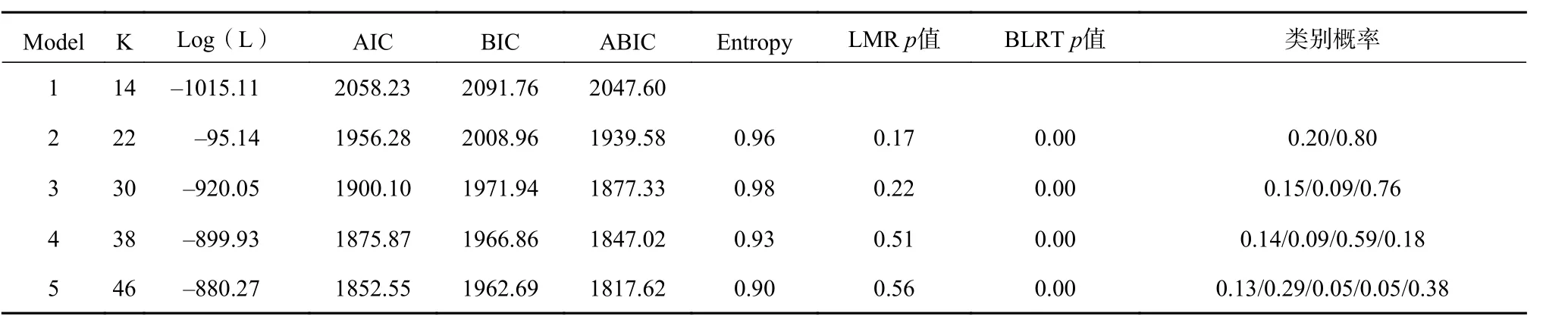
表 5 幼儿1 ～ 10 数线范围的潜在剖面（LPA）的各项指标比较

表 6 全体幼儿1 ～ 20 数线范围的潜在剖面（LPA）的各项指标比较

研究者根据潜在剖面图呈现出的估计模式及已有研究中常见的估计模式进行命名。由图1 可以看出，在1～5 数线范围内，四个类别的估计模式分别为：小数低估、大数高估的“拉伸模式”（Class1-7%）、基本接近标准值的“标准线性模式”（Class2-56%）、整体低估而呈线性的“非标准线性模式”（Class3-36%）和不规则的“其它模式”（Class4-1%）；在1～10 数线范围内，三个类别的估计模式分别为整体低估而呈线性的“非标准线性模式”（Class1-15%）、不规则的“其它模式”（Class2-9%）和基本接近标准值的“标准线性模式”（Class3-76%）；在1～20 数线范围内，两个类别的估计模式分别为：对数模式（Class1-91%）和其它模式（Class2-9%）。将幼儿在各个数线范围内进行数线估计任务时所使用的主要策略和其对应的估计模式进行统计，结果如表7 所示。从横向来看，每种估计模式使用频数最高的策略类别集中在“数字关系”和“数数”两种策略。尤其是在标准线性模式、非标准线性模式以及对数模式这三种估计模式中，“数字关系”策略的使用频率较高。从纵向来看，除了“不知道”这一类别外，其余四种策略种类中频数最高的都是标准线性模式。在标准线性估计模式中，使用频率较高的也是“数字关系”、“数数”策略。可见，达到标准线性估计模式的幼儿使用各种有效策略的频率较高，而“数字关系”和“数数”策略则是幼儿主要估计模式中最为常用的策略。

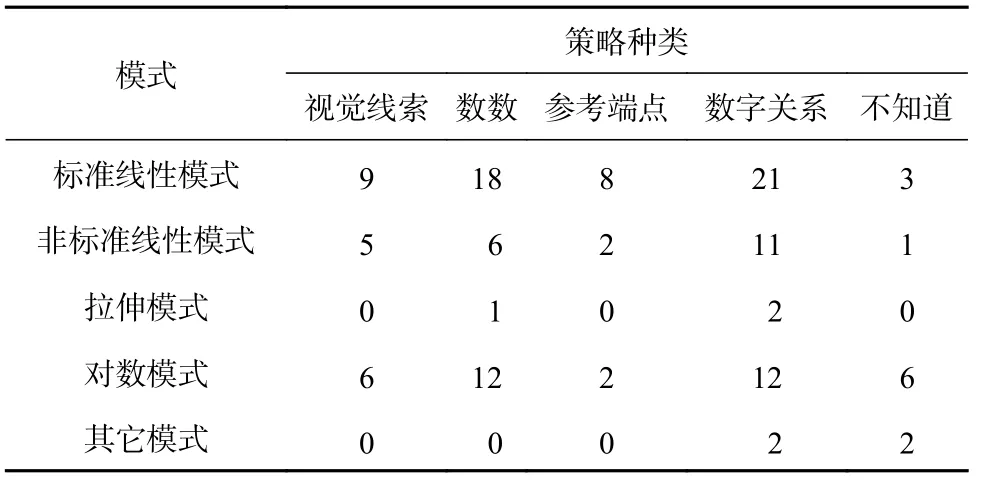
表 7 各估计模式策略种类分布表

4 分析与讨论

4.1 幼儿心理数线估计使用策略的特点

4.1.1 幼儿数线估计的策略具有多样性的特点

幼儿在进行数线估计过程中展现了丰富的策略，一方面体现在策略种类的多样化，研究者通过编码归类，共总结六种策略。另一方面，策略的多样性体现在幼儿对策略运用的多样化。测查中发现，同一幼儿在不同范围的数线估计任务中使用的策略有所不同，在同一数线范围不同数字的数线估计任务中使用的策略也有不同。部分幼儿在三个数线范围的17 个估计数字中能够表现出3～4 种不同的估计策略。

4.1.2 幼儿数线估计的策略具有差异性

首先，幼儿数线估计策略使用具有年龄差异。研究发现，小班幼儿使用“不知道”、“其它”两种较低水平策略的频率高于中班幼儿；而中班幼儿使用“数数”、“数字关系”两种较高水平策略的频率高于小班幼儿。在小班幼儿群体中，“不知道”和“其它”策略所占比例较大可能与幼儿的认知发展水平和语言表达能力有关。小班幼儿还不具备策略表达能力，不能对自身的思维进行反思，但是幼儿又要尽力给研究者一个答案，因此会出现各类和问题几乎没有相关性的答案。另一方面也可能是幼儿没有理解研究者提问的本意，不理解研究者的问题，而没有从数线估计任务本身来回答。但是测查中也发现部分小班幼儿能够使用“数数”、“数字关系”的策略，这也体现了幼儿心理数线发展的年龄差异性。中班幼儿对“数数”和“数字关系”策略的运用普遍多于小班幼儿表明，此年龄阶段幼儿开始认识到数量关系可以通过“数数”的方式来梳理和判断，而不仅仅是用眼睛看。这一变化趋势符合幼儿数概念的发展趋势，4 岁幼儿开始意识到数数和数字的位置是相关的（Sarama & Clements,2009），体现出此年龄阶段幼儿对数序、数距和数量关系的关注。

其次，幼儿数线估计策略使用具有情景差异。由于情景设置的不同，部分估计策略在特定情景中的使用频率显著高于其它策略，例如中班幼儿在情景一中使用“参照端点”策略显著高于情景二。

最后，幼儿数线估计策略使用具有数线范围差异。随着数线范围的扩大，“不知道”和“其它”策略的使用比例在不断增加；“参照端点”策略使用的比例在不断降低。这表明一些策略的使用受到数线范围影响。

4.2 估计策略与绝对误差百分比

研究发现，在1～5 和1～10 数线范围内，幼儿数线估计的绝对误差百分比不存在显著的策略差异。在1～20 数线范围内存在显著的策略差异，运用“不知道”策略的绝对误差百分比显著高于其它五种策略，即估计准确率显著低于其它五种策略；运用“其它”策略的绝对误差百分比显著高于“数数”策略。

“不知道”策略是指幼儿不能够回答自身策略。这部分幼儿可能并不理解研究操作或者不知道如何表达自己的策略，这一方面与幼儿的语言理解和表达能力有关，另一方面也可能与其日常的数学教育等有关。除了“不知道”策略，运用“其它”策略的幼儿在1～20 数线估计中的准确率显著低于“数数”策略。相比于“不知道”、“其它”策略，“数数”是一种更加有效的估计策略。一方面有效的策略能够辅助幼儿进行数线估计，提高数线估计的准确率。另一方面，关注到数字和数量关系的策略能够有效帮助幼儿降低估计错误。这也说明数数能够帮助幼儿建立对数字关系的理解，帮助幼儿逐渐发展心理数线，是心理数线建立过程中的重要策略。

4.3 估计策略与估计模式

首先，估计策略能够影响估计模式。例如中班幼儿在情景一中对“参照端点”策略的使用频率显著高于其它，其中1～5 数线范围的使用频率最高。而估计模式统计结果也显示，中班幼儿在1～5 数线范围内表现出较高比例的“拉伸模式”，这一模式的主要形成原因就是幼儿对两端端点的关注，这与幼儿整体的估计策略是紧密相关的。“参照端点”策略和“拉伸模式”表明幼儿认识到数量的起点和终点，是一种对数量范围的关注，认识到集合是有限的，而不是毫无边界的，表明幼儿开始具有初步的数量关系概念。

其次，各种估计模式中使用比例较高的是“数字关系”和“数数”策略。尤其是在标准线性模式、非标准线性模式以及对数模式这三种估计模式中，“数字关系”策略的使用频率最高。可见，“数字关系”和“数数”是幼儿数线估计中重要且有效的策略，对“数字关系”的理解和“数数”的掌握可以帮助幼儿把握数序和数距的关系。这也在一定程度上说明，能够熟练地数数和掌握数字之间的关系对于幼儿建立和发展心理数线具有重要的意义。

最后，“标准线性模式”中各种有效策略运用的比例最高。除了“不知道”策略之外，“标准线性模式”中其余四种策略的使用频率都高于其它模式类别。可见，达到标准线性估计模式的幼儿能够使用各种有效策略进行数线估计。“标准线性模式”是最为接近标准值的估计模式，达到这一模式是幼儿心理数线形成的标志。这一结果一方面表明运用有效的估计策略能够帮助幼儿形成线性估计模式，建立心理数线；另一方面也表明能够准确表达自身策略的幼儿，其估计模式水平更高，向标准线性模式趋近。

5 结论

本研究条件得到以下结论：（1）3～5 岁幼儿在数线估计任务中表现出丰富多样的估计策略，包括“视觉线索”、“数数”、“参照端点”、“数字关系”等策略；（2）幼儿数线估计策略具有年龄差异、情景差异和数线范围的差异；（3）估计策略与数线估计准确率、数线估计模式密切相关。

参 考 文 献

刘国芳, 辛自强. (2012). 数字线估计研究: “模型”背后的策略. 心理研究, 5(2), 27–33, doi: 10.3969/j.issn.2095-1159.2012.02.004.

Booth, J. L., & Siegler, R. S. (2006). Developmental and individual differences in pure numerical estimation. Developmental Psychology,42(1), 189–201, doi: 10.1037/0012-1649.41.6.189.

Bouwmeester, S., & Verkoeijen, P. P. J. L. (2012). Multiple representations in number line estimation: A developmental shift or classes of representations? Cognition and Instruction, 30(3), 246–260, doi:10.1080/07370008.2012.689384.

Crites, T. (1992). Skilled and less skilled estimators' strategies for estimating discrete quantities. The Elementary School Journal, 92(5), 601–619,doi: 10.1086/461709.

Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology:General, 122(3), 371–396, doi: 10.1037/0096-3445.122.3.371.

Ebersbach, M., Luwel, K., Frick, A., Onghena, P., & Verschaffel, L. (2008).The relationship between the shape of the mental number line and familiarity with numbers in 5-to 9-year old children: Evidence for a segmented linear model. Journal of Experimental Child Psychology,99(1), 1–17, doi: 10.1016/j.jecp.2007.08.006.

Laski, E. V., & Yu, Q. Y. (2014). Number line estimation and mental addition: Examining the potential roles of language and education.Journal of Experimental Child Psychology, 117, 29–44, doi: 10.1016/j.jecp.2013.08.007.

Link, T., Huber, S., Nuerk, H. C., & Moeller, K. (2014). Unbounding the mental number line—New evidence on children’s spatial representation of numbers. Frontiers in Psychology, 4, 1021.

Muthén, L. K., & Muthén, B. O. (2012). Mplus user’s guide (7th ed.). Los Angeles, CA: Muthén & Muthén.

Opfer, J. E., Thompson, C. A., & Kim, D. (2016). Free versus anchored numerical estimation: A unified approach. Cognition, 149, 11–17, doi:10.1016/j.cognition.2015.11.015.

Ramani, G. B., & Siegler, R. S. (2008). Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development, 79(2), 375–394, doi:10.1111/j.1467-8624.2007.01131.x.

Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research: Learning trajectories for young children. New York: Routledge.

Schneider, M., Grabner, R. H., & Paetsch, J. (2009). Mental number line,number line estimation, and mathematical achievement: Their interrelations in grades 5 and 6. Journal of Educational Psychology,101(2), 359–372, doi: 10.1037/a0013840.

Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children. Child Development, 75(2), 428–444, doi: 10.1111/cdev.2004.75.issue-2.

Siegler, R. S., & Mu, Y. (2008). Chinese children excel on novel mathematics problems even before elementary school. Psychological Science, 19(8), 759–763, doi: 10.1111/j.1467-9280.2008.02153.x.

Siegler, R. S., & Opfer, J. E. (2003). The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science, 14(3), 237–250, doi: 10.1111/1467-9280.02438.

Siegler, R. S., & Ramani, G. B. (2008). Playing linear numerical board games promotes low-income children’s numerical development.Developmental Science, 11(5), 655–661, doi: 10.1111/desc.2008.11.issue-5.

Simms, V., Clayton, S., Cragg, L., Gilmore, C., & Johnson, S. (2016).Explaining the relationship between number line estimation and mathematical achievement: The role of visuomotor integration and visuospatial skills. Journal of Experimental Child Psychology, 145,22–33, doi: 10.1016/j.jecp.2015.12.004.

Simms, V., Muldoon, K., & Towse, J. (2013). Plane thinking: Mental representations in number line estimation as a function of orientation,scale, and counting proficiency. Journal of Experimental Child Psychology, 115(3), 468–480, doi: 10.1016/j.jecp.2013.03.011.

Slusser, E. B., Santiago, R. T., & Barth, H. C. (2013). Developmental change in numerical estimation. Journal of Experimental Psychology:General, 142(1), 193–208, doi: 10.1037/a0028560.

Xu, X. H., Chen, C. S., Pan, M. M., & Li, N. (2013). Development of numerical estimation in Chinese preschool children. Journal of Experimental Child Psychology, 116(2), 351–366, doi: 10.1016/j.jecp.2013.06.009.