铝钢电阻单元焊接头力学性能模拟
2019-06-05何冠中马运五李永兵
何冠中,楼 铭,马运五,李永兵
(上海交通大学 机械系统与振动国家重点实验室;上海市复杂薄板结构数字化制造重点实验室,上海 200240)
随着全球能源危机和环境污染日益严峻,节能减排已成为现代汽车工业的重要发展方向.汽车能源消耗和尾气排放与车身重量直接相关,更轻质的车身可以有效减少油耗和二氧化碳排放量,同时还能提高操控性和动力等性能.因此,车身轻量化受到各大车企的广泛重视[1].综合考虑性价比,发展多材料复合车身已经成为车身轻量化的必然选择[2-3].其中,铝合金以密度低、比强度高、耐腐蚀性佳等优点,成为车身轻量化的首选材料.但是,铝合金等轻质材料的应用对传统钢制车身焊装的电阻点焊技术提出了巨大挑战[4].铝和钢在晶体结构和热物理属性上存在较大差异;而点焊时界面上易形成硬而脆的金属间化合物,导致难以获得质量可靠的焊接接头[5].自冲铆接作为一种无热效应的机械连接工艺,是当前全铝和铝钢混合车身的主要连接技术[6].然而在连接一些高强度、高硬度材料,如超高强钢时,自冲铆接由于设备吨位和铆钉自身材料特性的制约,无法获得具有高质量机械互锁的接头[7].
基于上述问题,Meschut等[8]提出了一种电阻单元焊(REW)工艺,以实现铝合金和钢之间的有效连接.电阻单元焊基本原理为利用辅助单元将异种金属的连接问题转变为同种金属焊接问题.其工艺过程包括:① 根据铝板厚度、待焊钢板材质等条件,选择尺寸、材质合适的铆钉作为辅助单元;② 用辅助单元对铝板的待连接部分进行冲裁置钉;③ 将待焊钢板放置于铝板下层,利用传统电阻点焊电极对铝板上的预置铆钉和下层钢板进行熔化焊接;④ 在钢制铆钉底部与钢板之间形成焊核,并配合铆钉头部把铝板锁在铆钉与下层钢板之间.
由于电阻单元焊是一种新型异种材料连接技术,目前国内外公开的相关研究相对较少.Meschut等[9]利用多种新工艺对铝合金和超高强钢进行连接,发现REW工艺不受超高强钢变形抗力大而难以形成有效机械自锁的影响,在与结构胶复合使用时能获得比自冲铆接更强的拉剪强度.凌展翔等[10-11]对铝合金和硼钢进行REW连接,发现其接头拉剪强度远高于传统的电阻点焊,同时研究了REW接头硬度分布规律,以及接头失效模式.

图1 焊接前后电阻单元焊接头几何断面形貌Fig.1 Cross-section profiles of REW joint
现有研究均是通过试验手段来分析REW接头强度.近年来,已经有部分学者对超高强钢点焊接头的力学性能进行了模拟研究[12-13],但是,REW接头涉及同种材料熔化焊以及异质材料机械互锁的双重连接,其接头形貌和失效机理均较为复杂,同时为研究接头力学性能而制作不同铆钉、测试不同焊接参数将耗费巨大精力与时间.因此,利用有限元方法来模拟REW接头的力学试验过程,研究接头力学特性是获取REW接头失效机理,降低工艺开发的物力和时间成本的首选方法,而此方面研究目前尚属空白.为此,本文通过建立REW接头力学性能有限元模型,研究接头拉剪和剥离试验过程中接头形貌的演化规律,分析接头中应力应变分布规律和失效行为,揭示接头失效机理.
1 模型建立
首先依据铆钉、铝板和钢板的实际形貌尺寸,在CATIA软件中建立相应的三维几何模型.然后将其导入HYPERMESH中划分网格、生成LS-DYNA关键字k文件,并在LS-PREPOST中编辑相应关键字.完成模型前处理后,提交LS-DYNA求解器进行求解计算.计算完成后在LS-PREPOST中查看并分析结果.
1.1 几何建模与网格剖分
本文以厚度为1.4 mm的铝合金AA5182和厚度为 1.0 mm的冷轧钢 CR340所组成的铝钢异种材料匹配为研究对象.在铆钉预置入铝板后,利用伺服焊枪对钢制铆钉和下层钢板施焊,焊接电流为 8.5 kA、焊接时间为240 ms、电极压力为 2.8 kN.
REW力学性能建模的关键在于其接头形貌的处理,由于焊接时存在材料软化变形和焊核形成等复杂过程,焊接前后铆钉形貌已发生变化,焊接前后接头断面如图1所示.由图可见,焊前铆钉及铝板的断面形貌较为规整,铆钉腿部垂直于铝板表面,同时铆钉腿部与铝板下表面周围留有落料模凸台形成的空隙.焊接时,电极帽对接头加压通电,随着温度升高,材料软化,铆钉产生了较大变形,之前垂直于板材表面的铆钉腿部受压变形,并挤压断口处铝板填充落料模凸台空隙,形成一个斜面,最终铆钉腿部中心区域与下层钢板局部熔化形成熔核.使用2%硝酸酒精溶液对焊后接头断面腐蚀15 s之后,采用 LeicaS8APO 体视显微镜观察接头断面形貌(见图1(b)),发现因铆钉高度较高,与钢板焊接时类似于差厚板点焊,导致焊核形成偏向于铆钉一侧,铆钉和钢板均产生较大面积的热影响区.铆钉与钢板熔核下边界处形成一个类梯形结构,梯形长底边的实际连接长度约为 3.2 mm左右.
综合考虑焊接前后断面的形貌特征,对接头建模进行一定理想化处理,接头模型如图2所示.接头整体上部外轮廓参考焊前形貌,对铆钉头部和板件做平整处理.由于焊后接头处微观组织和材料特性已经发生变化,将铆钉和钢板在熔焊过程中的硬化部分作为单独部件处理.同时,对于焊核周围连接细节,模型完全复刻实际的铆钉嵌入钢板的梯形特征,并采用合并铆钉底部与钢板接触的梯形界面上结点的方法以模拟熔核的效果,如图2(b)中虚线所示.
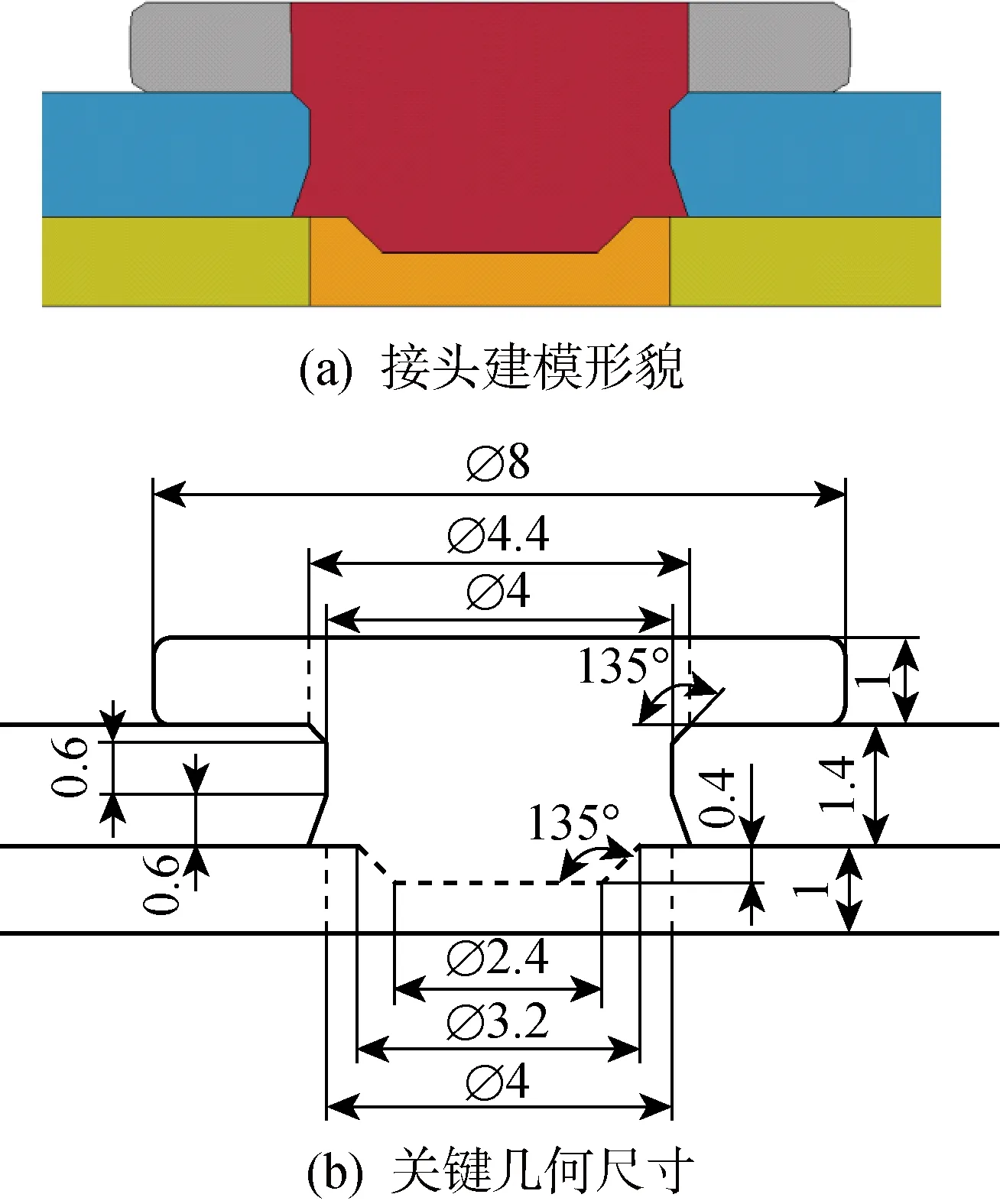
图2 电阻单元焊接头建模及关键几何尺寸 (mm)Fig.2 Geometrical model of REW joint and key dimensions (mm)
本模型中各部件均为镜像对称,为了提高计算效率、节省时间,同时便于观察力学性能测试时接头内部形貌的演化规律,将带接头试样模型由对称面一分为二开展模拟研究.针对实际拉剪和剥离试验中所用试样的整体尺寸,分别建立有限元模型如图3所示.设定拉剪和剥离试验中两板交叠区长度为38 mm,接头布置于两板交叠区中心,固定装夹区长度为40 mm.
试样各部件均定义为三维实体单元,拉剪和剥离模型的网格划分策略如图4所示.为同时保证模拟精度和计算效率,焊核周围区域网格最细密,大小为 0.1 mm,近接头区域铆钉及钢板网格尺寸为 0.2 mm.远离接头部分依重要性做适当稀疏处理,铝板和钢板交叠区主体网格尺寸设定为 1.2 mm,而两板装夹区网格大小设定为 2.5 mm.拉剪模型单元数为 20 950,节点数为 26 002.剥离模型单元数为 20 622,节点数为 24 602.
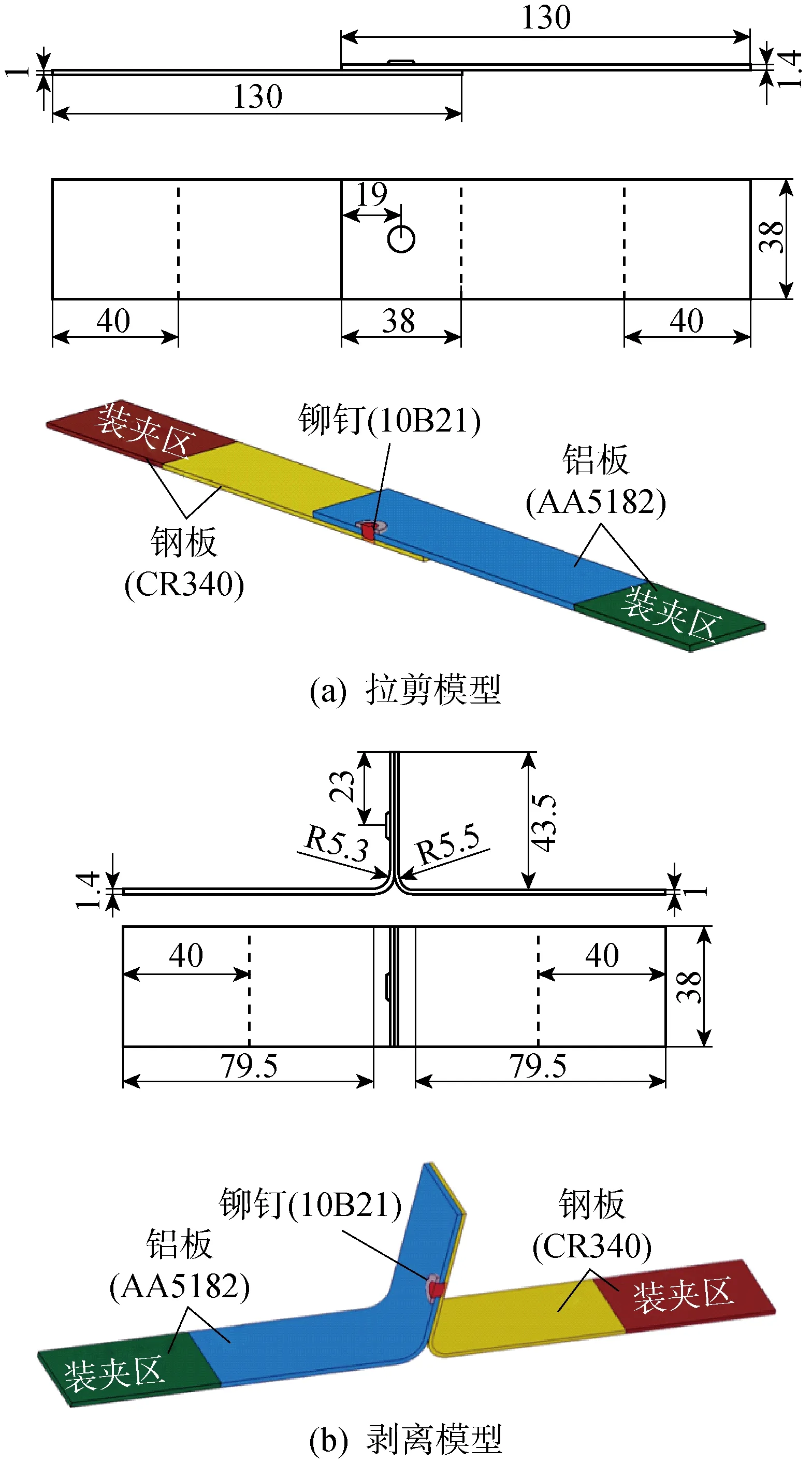
图3 电阻单元焊力学性能测试样品示意图(mm)Fig.3 Schematic of REW specimen configuration with dimensions (mm)
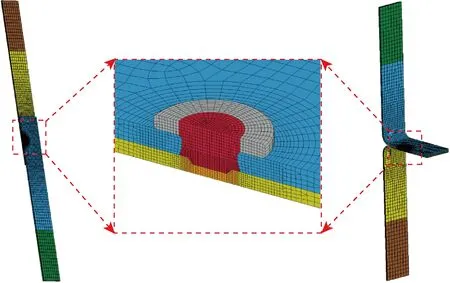
图4 拉剪和剥离模型网格剖分Fig.4 Mesh strategy of REW lap-shear and coach-peel specimens
1.2 材料特性及失效判据
本研究所用铝合金板材AA5182、钢板CR340和通过多冲程冷镦工艺制备而得的钢制铆钉母材10B21的材料属性如表1所示.
铝板和钢板的材料力学参数均通过实际力学试验曲线获取,钢制铆钉则采用双线性模型.由于焊接后形成的焊核及热影响区微观组织结构发生改变,其材料力学性能相较母材有了较大变化,而焊核几何尺寸小且形貌不规则,难以通过材料力学试验直接获取其力学性能参数,为此本文通过测量受焊接热循环影响的材料与母材硬度的比例关系来反推材料的屈服强度和拉伸强度[14-15].本研究利用维氏硬度计测量REW接头的硬度分布规律,分别选取了铆钉头部、上层铝板和下层钢板沿厚度方向的中心线进行测量,每条线上的测试点间隔为 0.3 mm,测试点分布及结果如图5所示.可以看出,无论对于钢制铆钉还是钢板,其焊核与热影响区之间的硬度差别不大,可以将其简化为一个整体的实体强化区.测量得铆钉强化区和原始母材的平均硬度分别为476和281,按硬度比例关系缩放得到铆钉强化区的屈服强度和拉伸强度分别为830和 1 306 MPa.同样,钢板强化区与其母材硬度分别为376和218 HV,按硬度比例关系缩放得到钢板强化区的屈服强度和拉伸强度分别为673和931 MPa.有限元模型中使用的各材料等效塑性应力(σ)-应变(ε)曲线如图6所示.

表1 有限元模型中材料属性Tab.1 Material properties of FE model
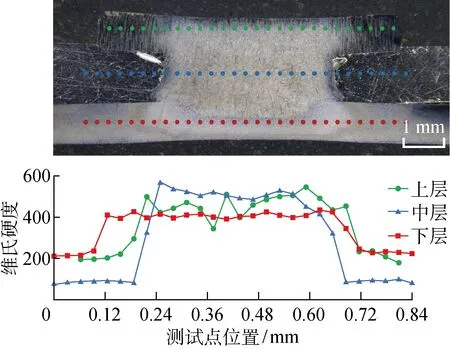
图5 电阻单元焊接头几何断面形貌及硬度分布Fig.5 Cross section and hardness profile of REW joint
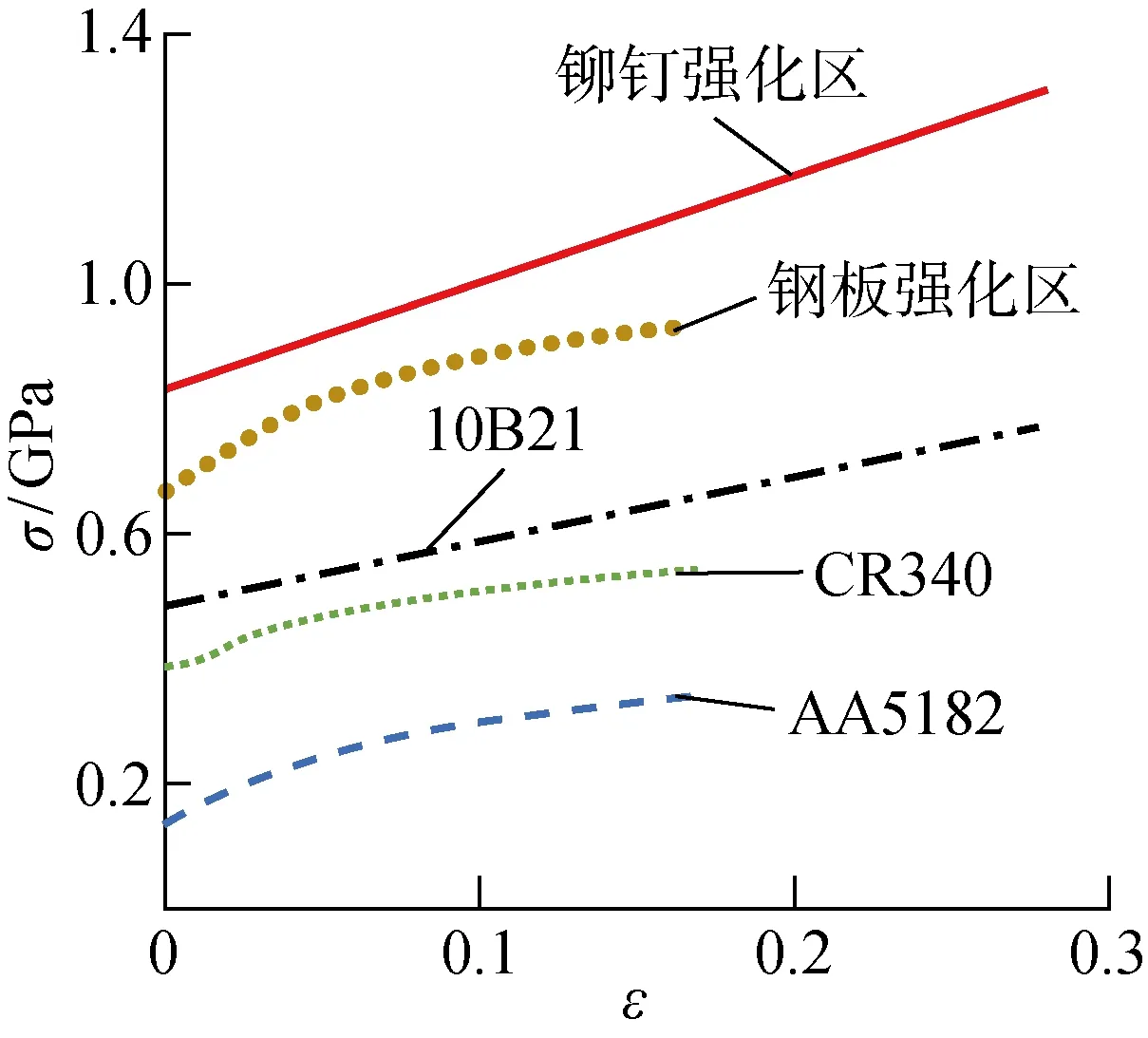
图6 有限元模型中材料的等效塑性应力-应变曲线Fig.6 Effective plastic stress-strain curve of materials in FE model
为模拟拉剪和剥离试验中的裂纹扩展过程,使用关键字MAT_ADD_EROSION设置材料的失效准则,并在有限元模拟过程中对失效单元进行删除来模拟材料的断裂过程.在实际试验中发现,接头的失效模式是纽扣断裂,其失效位置位于焊核周围的钢板上,因此本模型只定义钢板硬化区为可失效部件.CR340钢板的材料失效参数参考文献[16]中的结果,得到其有效塑性应变随应力三轴度的变化规律.由于拉剪和剥离试验中材料受力方式及应力三轴度不同,分别对拉剪和剥离模型选取有效塑性应变ε=1.0 和ε=0.6 作为失效条件.
1.3 边界及求解条件设置
本模型中的铝合金板、钢板以及钢制铆钉均设为变形体.模型中各部件的接触均设置为网格双向面对面接触,其LS-DYNA关键字为FORMING_SURFACE_TO_SURFACE_MORTAR.各界面间摩擦采用库伦模型描述,考虑到实际接头中铝板与铆钉接触面为过盈配合,因此将模型中铝板和铆钉硬化区接触的摩擦系数取 0.35,将其余接触面的摩擦系数设为 0.2.模型边界条件如图7所示.鉴于镜像模型的对称性,约束模拟过程中对称面上所有单元节点的Z轴方向位移不变.固定下层钢板装夹区全部节点自由度,拉剪模型中约束上层铝板装夹区所有节点除向X轴方向移动外所有自由度,同样地,剥离模型中约束铝板装夹区所有节点除向Y轴方向移动外所有自由度.为了缩短模拟时间,提高计算效率,采用增加位移载荷速度配合质量缩放的方法[17],对于拉剪模型中的铝板装夹区施加X轴匀速正向位移载荷6 mm/s,对于剥离模型中的铝板装夹区施加Y轴匀速正向的位移载荷30 mm/s.设置求解时间约为1 s,求解时间步 0.005 s.
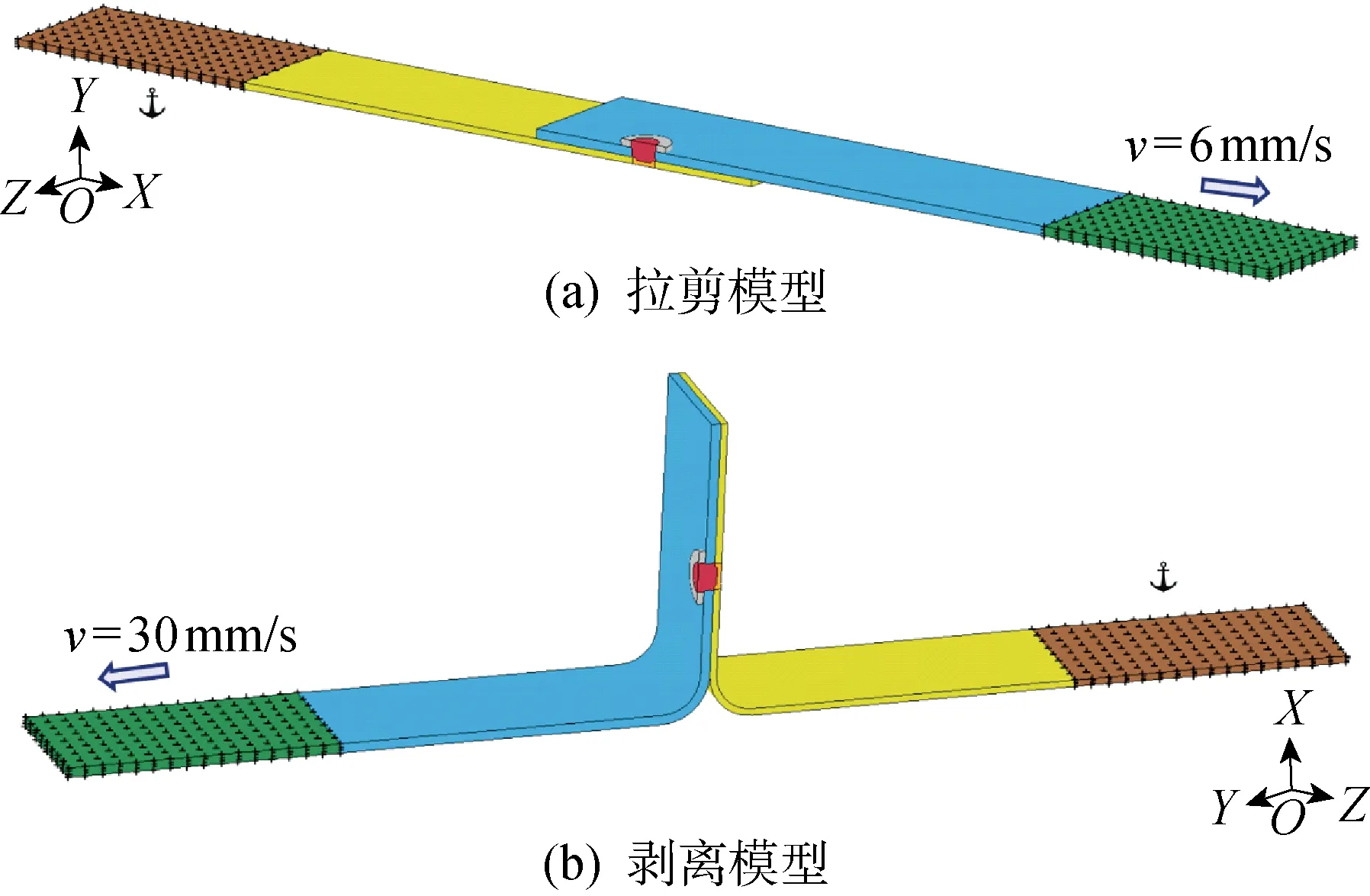
图7 有限元模型边界条件Fig.7 Boundary conditions of FE-models
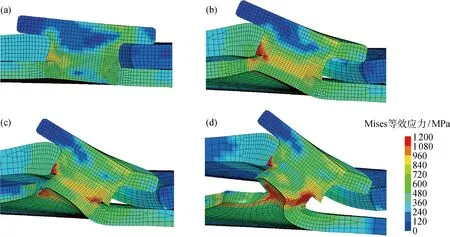
图9 拉剪过程Mises等效应力演化Fig.9 Simulated geometry and von Mises stress evolution of REW lap-shear process
2 拉剪结果分析
为验证拉剪模型的准确性,在电子万能拉伸机上对REW试样进行拉剪试验,试验重复次数为3次,得到拉剪强度分别为 5.722、5.778 和 5.789 kN,即REW接头平均拉剪强度为 5.763 kN,而有限元模拟计算得最大拉剪强度为 6.002 kN,比试验值高约 4.1%,模拟结果与试验值相吻合.相应的拉剪力-位移曲线与模拟计算得到的结果对比如图8所示.由图可见:模拟所得拉剪力(F)-位移(L)曲线与试验曲线的变化趋势上具有较好的匹配度;从局部特征来看,试验曲线在拉伸位移达到1 mm左右时普遍存在小陡降,而后再上升的过程,而模拟曲线未能准确表征该现象.分析其原因主要是模型在建模时进行了一定的简化处理,即没有考虑焊接时接头内其它连接形式,如铆钉/铝板或铝板/钢板间金属间化合物层的影响,认为拉伸初期出现的小陡降再上升现象很可能是由铝钢脆性金属间化合物断裂造成的.总之,有限元模拟结果在强度和位移方面与试验结果均大致吻合,模型的准确性得以验证.
选取图8中模拟拉剪力-位移曲线上的4个重要节点,其对应的接头形貌及应力场演化过程如图9所示.由图可见,REW接头拉剪过程可以划分为3个阶段.第1阶段,从起始经A点至B点,该阶段铝板装夹区被匀速拉伸导致铆钉左侧铝材受剧烈挤压变形,在力矩的作用下铆钉旋转,拉动接头一侧的下层钢板旋转上移.在这一过程中,钢板硬化区网格发生较大形变,焊核边界位置形成主要应力集中区.第2阶段,当位移达到3.3 mm后,曲线进入BC段,近焊核周围的钢板硬化区单元的有效塑性应变达到了设定的失效值,最大应力超过 1.2 GPa,此时网格开始失效、曲线不再上升从而维持在6 kN左右抖动.第3阶段,当位移达到 4.38 mm后曲线进入CD段,失效的网格首次完全贯穿钢板上下表面,裂缝的形成导致拉剪力-位移曲线出现陡降,最后裂纹沿焊核的周向扩展.接头最终形貌特征为铆钉发生显著旋转,其一侧头部受铝钢挤压向上翘起,底部连同部分钢板硬化区被半拉拔出钢板.
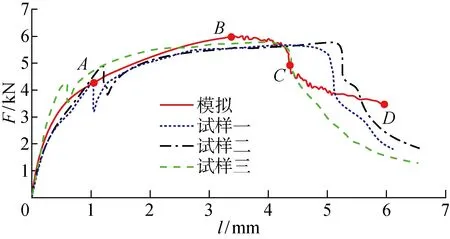
图8 拉剪模拟和试验的拉剪力-位移曲线对比Fig.8 Comparison of force-displacement curves of modeling and specimen
图10所示为本研究REW接头拉剪试样的断口形貌.其断裂模式为纽扣断裂,即铆钉连同焊核下方部分钢板被上层铝板一并拉出,在钢板中留下空孔.仔细对比最终接头断口形貌后发现,模型在两板交叠区翘起方式、铆钉头部形变程度和铆钉转动角度等因素上都较为吻合,也进一步验证本研究所建立的拉剪有限元模型可以有效模拟REW接头拉剪过程的应力、应变和接头几何形貌等宏微观特性的演化规律,预测接头的失效区域,为工艺优化提供借鉴.

图10 拉剪试验断口形貌Fig.10 Failure modes of REW joints after lap-shear test
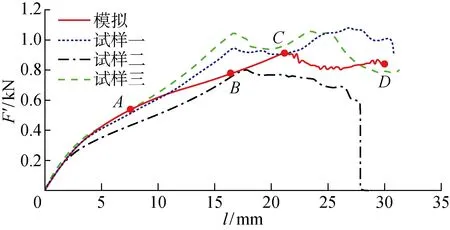
图11 模拟和试验的剥离力-位移曲线对比Fig.11 Comparison of force-displacement curves of modeling and specimen
3 剥离结果分析
类似地,在电子万能拉伸机上对REW试样进行剥离试验,3次重复试验得到剥离强度分别为 945.8、766.7 和 1 051.1 N,计算得到REW接头平均剥离强度为 921.2 N.有限元模拟得到的最大剥离强度为 915.1 N,比试验平均值低约 0.7%,两者大小十分接近.模拟结果与试验的剥离力(F′)-位移曲线对比如图11所示.模拟曲线斜率类似试验曲线的增大-减小-再增大趋势,其最大剥离力与试验平均值相近,而其对应的位移则稍大于试验中的位移值.分析其原因主要是简化模型时未能考虑焊接后接头内焊核及热影响区的精确范围和材料实际参数,导致接头在断裂位移有所延伸.总之,有限元模拟结果在强度和位移方面与试验结果均大致符合,本模型准确可信.
选取图11中模拟剥离力-位移曲线上的4个重要结点,其对应接头形貌和应力场演化过程如图12所示.不同于拉剪,剥离试验中铝板和钢板都有较为严重的变形.类似地,模拟剥离过程也可以划分为3个阶段.第1阶段,从起始经A点至B点,此时铝板装夹端向上匀速拉伸,铆钉左侧头部受铝板挤压作用而翘曲,同时钢板在铆钉向上拉拔和铝板交叠区挤压的共同作用下,焊核周围硬化区强烈弯曲变形,整个接头向上移动.第2阶段,位移达到 17.1 mm后,曲线进入BC段,焊核边界处的钢板硬化区单元的有效塑性应变达到设定值,材料开始失效,裂纹产生并向下延伸.第3阶段,位移达到21 mm后,曲线进入CD段,失效网格首次贯穿钢板上下表面,剥离力-位移曲线开始逐渐下降,当裂纹沿焊核圆周切向扩展到平行于对称面时,转而向钢板母材区扩展,剥离力-位移曲线稳定在850 N左右;D点对应最终接头形貌,此时位移为30 mm,铆钉半拉脱出下层钢板母材,其中铆钉头部在铝板的挤压作用下向上弯曲,钢板断口为焊核边界的1/4圆环区域.
REW剥离试样断口形貌如图13所示.其断裂模式为纽扣断裂,即铝板带动铆钉向上匀速拉伸,铆钉连带焊核周围部分钢材一起从母材拉出.不同于一般纽扣断裂中留下的圆形空孔,本研究中铆钉初步拉出豁口后,裂纹沿焊核圆周切向扩展,转而将下层钢板沿条状拉穿至边界.对比最终接头断口形貌,模型在两板交叠区弯曲程度、裂纹产生位置等因素上都与试验较为相似,且模型已经表征了接头发生纽扣失效后铆钉连带部分钢板硬化区从下层钢板脱出的趋势.进一步验证了本模型对接头剥离过程中应力应变分布和几何形貌演化规律的准确性,对预测接头失效区域和优化工艺提供了有效基础.
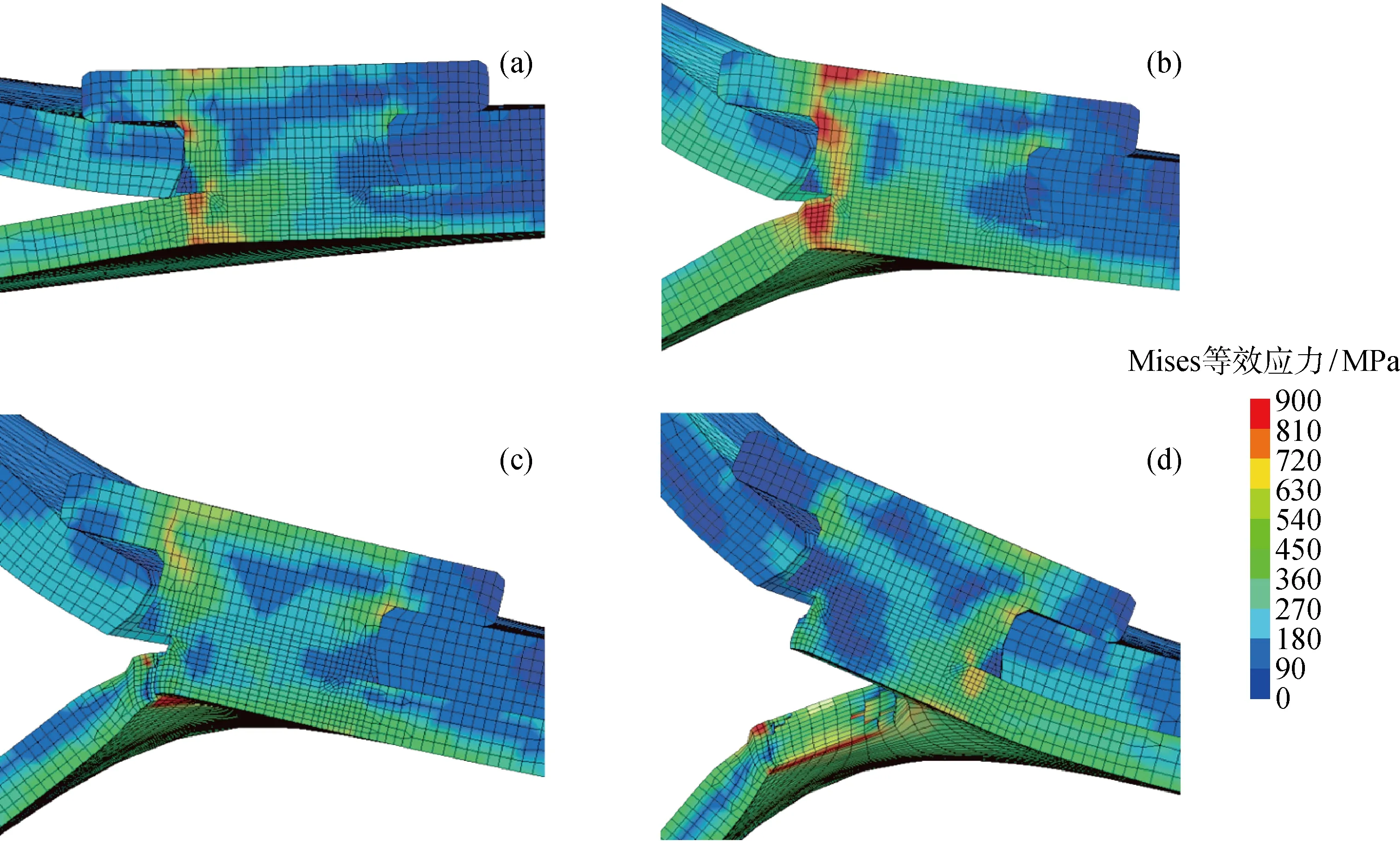
图12 剥离过程Mises等效应力演化Fig.12 Simulated geometry and von Mises stress evolution of REW coach-peel process
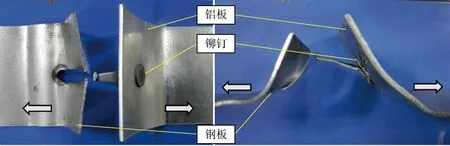
图13 剥离试验断口形貌Fig.13 Failure modes of REW joints after coach-peel test
4 结论
本文针对REW接头力学性能,利用有限元模拟分析手段,研究了拉剪和剥离试验中的接头应力应变变化规律,揭示了接头失效模式和断裂机理.研究得到的主要结论如下:
(1)电阻单元焊接头中焊核位置偏向于铆钉一侧,铆钉和钢板均有较大的矩形热影响区,铆钉底部与下层钢板连接界面处为一个梯形结构;
(2)拉剪试样应力集中主要出现在铆钉与下层钢板形成焊核边沿,拉剪过程中此处的下层钢板失效,铆钉连带焊核附近钢材拉出,形成纽扣断裂;
(3)剥离试验时钢板和铝板都产生较大形变,裂纹于焊核附近钢板硬化区产生,铆钉与焊核周围钢材一起将下层钢板拉穿至钢板边界,断裂模式为纽扣断裂.
