考虑资源空窗期的资源投入问题的建模与优化
2019-06-05陆志强
陆志强,石 婷
(同济大学 机械与能源工程学院,上海 201804)
飞机制造对于促进科技实力进步、带动国民经济发展和提升国家综合实力有着重要的意义.飞机的移动装配过程复杂,装配工序繁多,传统的经验式调度安排往往导致线边资源的极大浪费.因此,研究飞机移动装配相关基础问题的建模与科学决策,可以优化各装配任务的作业时间,有效降低装配过程的成本.事实上,装配线上任何单架飞机总装过程调度决策的基础问题都可看作是一个资源受限项目调度问题(RCPSP),各装配作业任务可认为是完成这个项目的活动,完成各装配作业任务所需的线边装配人员、工装、工具及仪器设备等可视为是完成项目所需的各类资源.资源投入问题作为该问题的对偶问题,其决策是以预定的工期期限作为约束来控制的,旨在获得较低的资源投入成本.该问题最早由Mörhing[1]提出,证明了此问题为NP-hard问题,并以求解RCPSP问题的算法为基础,设计了求解该问题的图解精确算法.Demeulemeester[2]同样参照对RCPSP问题的研究,将他与Herroelen[3]共同提出的基于深度优先的求解RCPSP问题的分支定界算法进行了改进,构建了求解资源投入问题(RIP)的优化算法.由于精确算法在求解该类问题时效率差,无法有效处理大规模问题,因此学者们相继设计了相关元启发式算法.Yamashita等[4]最早提出求解该问题的元启发式算法,将Multi-Start启发式算法和分散搜索(Scatter Search)过程相结合,用以修复不可行解并通过路径重连提高解的质量.Najafi等[5]提出了以各作业浮动时间为编码方式的遗传算法,在解码阶段设计了2种局部优化操作.Van等[6]设计了求解该问题的人工免疫算法,为避免早熟对资源列表及变异操作进行了改进.吴怡薇等[7]以遗传算法为框架,提出非关键任务调度优先级规则,利用区间细分、全局影响评估任务可排区间.Zhu等[8]将RIP问题拆分成排序和资源决策两类子问题,通过设计邻域搜索、路径重连及2种启发式算法来求解相应的子问题,并通过算例实验验证了算法的有效性.
现有文献中对于RIP问题的研究都以研究RCPSP问题的算法为框架,主要存在2点不足:① RCPSP本身也是NP-hard问题,对于某一资源水平,无法准确判断该资源下调度结果能否满足RIP的工期限制;② 在资源投入调度方面,对资源组合的搜索方向性不强,不能充分利用迭代过程中的信息使算法向最优解方向收敛,同时也导致算法效率低.因此,本文在算法设计中首先通过搜索算法直接确定各作业开始时间来间接获得项目资源投入量,避免了对资源大范围低效率的搜索;其次,根据迭代过程中的信息,对遗传算法变异操作进行改进,提出基于概率分布的作业开始时间选择方法,不断优化资源使用量,为进一步降低所得目标值,设计分支定界算法用以优化部分作业的开始时间.
另一方面,装配线上任何一架飞机装配的总周期时间一般都很长,线上资源特别是关键人力资源通常需要在同架飞机(同一项目)和线上不同架飞机(不同项目)的作业任务之间共享,因此,往往会存在因所需资源紧缺而必须延迟调度的情形,本文将资源存在的不可用时间段称为资源空窗期.胡淑芳[9]考虑资源时间窗和作业可拆分特性,设计了求解小规模单技能及多技能项目调度问题的分支定界算法.Lu等[10]结合微软的项目调度软件,说明资源日历对项目作业最早开始时间的影响,分析了4种时间关系在资源日历下的延迟.Jirachai等[11]研究了作业可拆分在考虑资源空窗期的多模式RCPSP问题中对调度结果的影响,设计了求解小规模该类问题的分支定界算法.针对项目调度中部分资源存在不可用期的这一实际,本文在设计求解基础RIP问题算法的基础上,参照求解带资源空窗期的RCPSP问题的研究方法,考虑资源存在提前已知的空窗期约束,并着重分析空窗期的引入对问题及算法设计的影响,提出适用于该问题的带局部分支优化操作的遗传算法.
1 问题描述及数学模型
1.1 问题描述
项目由J项作业构成,作业间存在着一定的时序关系,各作业仅在满足时序约束并且所需资源充足的条件下才可开始执行.记给定项目工期上限为T,作业集合A={1,2,…,J},每项作业j(j∈A)的执行时间为dj,Bpre(j)为项目中第j项作业的紧前作业集合,Bsuc(j)为其紧后作业集合.全部作业共享K种可更新资源,构成资源种类集P={1,2,…,K},同一种类下的所有资源皆一样.每种资源p的单位使用成本为Cp(p∈P),Wp为第p类资源下所有资源在项目工期T内的可用时间窗集,引入参量Zpt,Zpt=1表示资源p在t时刻可以使用,即t∈Wp,否则Zpt=0.各作业j所需要的资源种类为集合Mj,该集合大小为Sj,rjp表示作业j需要的单位资源p(p∈Mj)的数量.Rtp表示各作业在时刻t对资源p的使用量之和.对时间进行了离散化处理,模型的求解目标是优化项目周期内各资源p的使用成本.
1.2 数学模型
(1)
(2)
∀t∈Wp,∀p∈P
(3)
∀j∈A,∀t∈T
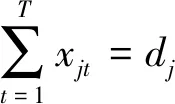
(4)
(5)
∀j*∈Bpre(j),∀t∈T
txjt≤T∀j∈A,∀t∈T
(6)
(7)
∀j∈A,∀t∈T
xjt={0,1} ∀j∈A,∀t∈T
(8)
式(1)为目标函数,表示最小化整个周期内资源使用总成本.式(2)可以计算各资源p在其可用时间窗Wp内的使用量.式(3)表示作业只有在所需资源皆可使用的情形下才能执行.式(4)表示作业在整个项目工期内的执行时刻必须满足该作业工期要求.式(5)表示时序约束,即作业必须在其所有紧前作业完成后才能进行.式(6)表示所有作业的最晚结束时间不应大于项目给定工期.式(7)表示作业一旦开始执行就不能中断.式(8)定义了决策变量xjt的可行域,作业j在时刻t执行时xjt=1;否则xjt=0.
2 算法设计
用RCPSP问题的求解思路解决RIP问题的算法设计中都以资源组合进行编码,采用某种优先级规则下调度生成机制的解码方式来评判各组合在给定工期上限内的可行性,由于对应每一编码下的子问题仍是NP问题,简单的启发式算法所得结果往往较差,从而增大将可行资源组合判定为不可行的几率,不利于求得较好的目标值.本文算法设计中避免了由资源解码得到作业调度计划的过程,通过直接确定作业开始时间的方式来间接获得项目中的资源投入量,解码算法中只需根据各作业执行位置计算各时刻资源消耗.考虑到后续的局部优化操作,故对项目工期内各时刻执行的作业进行编码.以遗传算法为搜索框架,充分利用迭代过程中作业不同开始时间对应不同目标值的信息,设计基于不同执行位置概率分布的作业开始时间选择方法来改进变异操作,使资源使用量向最优解收敛.在遗传算法求得较优可行解的基础上,针对所得列表,以各资源最大用量的时刻为起始点,考虑资源空窗期的影响,对后续相邻作业进行局部分支定界搜索,通过部分作业的重调度来进一步降低资源使用量.
算法框架如图1所示.图中:M为未改进代数;m为未改进代数阈值.

图1 算法框架Fig.1 Algorithm framework
2.1 空窗期分析
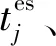
(9)
i∈Bpre(j),j=1,2,…,J
(10)
i∈Bsuc(j),j=1,2,…,J
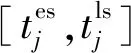
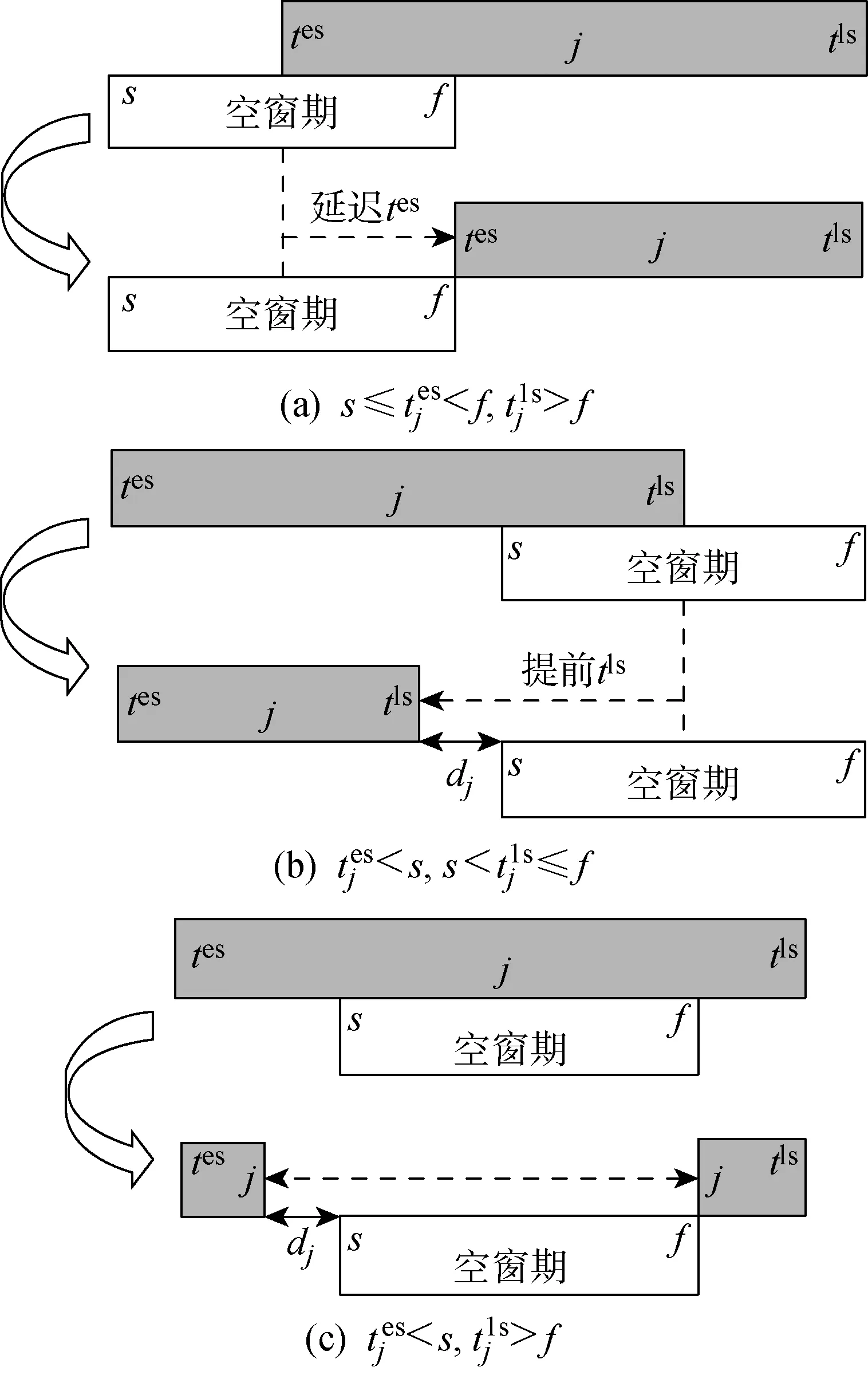
图2 资源空窗期影响作业开始时间示意图Fig.2 The diagram of starting time of the job affected by the resource vacations
由此可见,当作业所需资源存在空窗期且影响作业开始时间的决策区间时,空窗期的引入会导致作业的可排区间进一步缩小,降低作业调度的灵活性,影响调度结果,从而加剧空窗期前后位置的资源投入量,增加项目的成本支出.为优化考虑资源空窗期对项目调度的影响,解决此类资源投入问题,本文提出以下遗传算法及局部搜索算法进行求解.
2.2 遗传算法
2.2.1基于作业位置的编码 本设计中采用对作业位置进行编码的方式,项目工期上限为T,则编码长度为T段,编码第i段表示该时刻t下开始执行的作业集合,各编码段集合大小不一.每一编码段i上的作业集合必须保证各作业之间没有紧前关系,且其紧前作业在该编码段之前已执行完毕.以图3(a)所示算例为例,该网络图下的一种可行编码方式为3(b),其中作业2~7的开始时间分别为2、0、0、5、4和8.
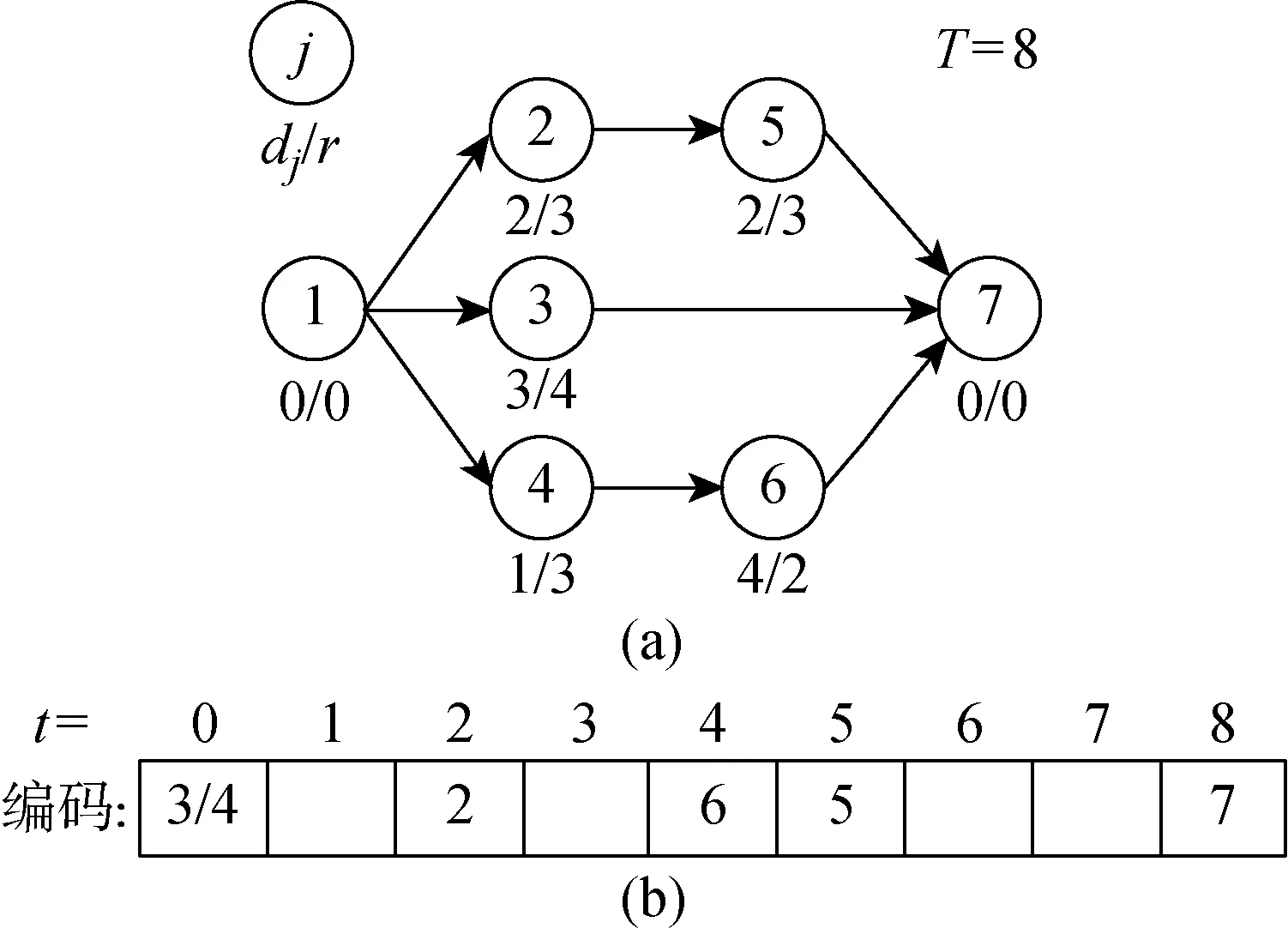
图3 编码示例Fig.3 Example of code
染色体生成步骤如下:
(1)定义时刻t=0,已排作业集Y={1},可排作业集H=∅,未排作业集N={1,2,…,J};
(2)若t=T,转步骤(5);否则,寻找t时刻紧前作业已完成的作业,加入可排作业集H,并将该作业从未排作业集中删除;
(3)寻找可排作业集H中各作业的全部组合形式,加入集合B;
(4)随机选择集合B中的一种作业组合,作为时刻t的执行作业集,令t=t+1,A=∅,更新集合Y和N,转步骤(2);
(5)输出编码列表.
2.2.2单点交叉 在经过轮盘赌选择机制获得的种群中,根据交叉概率Pc选择需要进行交叉操作的染色体组成集合C,
Pc=
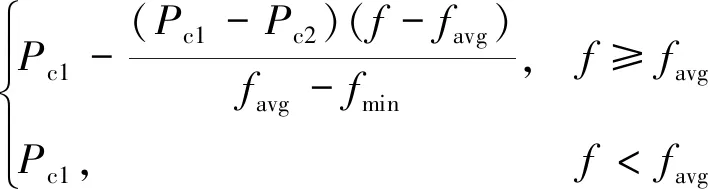
(11)
式中:Pc1和Pc2均为预先定义的常数;favg和fmin分别为所有染色体的平均适应度值和最小适应度值.
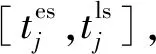
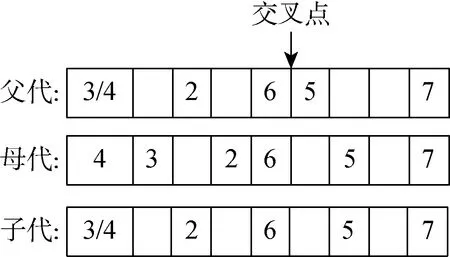
图4 交叉操作Fig.4 Crossover operation
2.2.3基于作业执行位置选择概率的变异 对经过交叉之后得到的染色体,根据变异概率Pm选择需要进行变异操作的染色体组成集合G,Pm同样通过式(11)求得.
对集合G中的染色体,本文设计了一种在迭代中改进作业开始时间的变异机制,通过不断调整迭代过程中各作业可排区间内各开始时间取值的概率,排除会产生极大资源用量的作业开始时间值,进一步缩小搜索空间,从而找到更好的作业调度方案.
定义染色体中变异作业μ开始时间选择概率Ptsμ(tes≤ts≤tls)和该开始时间下需要多投入的资源量Rtsμ.在初始种群中,令Rtsμ=1.之后的每条染色体,都根据当代的资源用量R更新Rtsμ:
Rtsμ=Rtsμ+max{0,R-R0}
(12)
染色体中需要变异的作业的开始时间ts被选中的概率为
(13)
式中:R0为当前得到的最低资源用量.
在迭代过程中,资源用量越大的作业开始时间ts对应的Rtsμ会不断增大,使得其被选中的概率Ptsμ不断减小;反之,越接近R0的作业开始时间对应的Rtsμ较小,使得相应Ptsμ被选中的概率变大,由此可以不断缩小作业开始时间的决策区间,使得作业调度向着产生更好的解的方向收敛.
综上,遗传算法步骤如下:
(1)初始化种群,令迭代次数λ=0,当前资源投入量为X;
(2)判断λ<λmax,若是,转步骤(3);否则,转步骤(7);
(3)对各染色体进行解码,求得相应的资源使用量;
(4)采用3.2.2和3.2.3中的交叉和变异机制生成新的种群;
(5)计算新生成个体的目标函数值,更新X;
(6)运用轮盘赌选择算子产生下一代种群,λ=λ+1,转步骤(2);
(7)输出X.
2.3 局部优化算法
在遗传算法所得作业调度方案的基础上,为进一步优化调度结果,降低资源投入成本,本文提出以分支定界算法为框架的局部优化操作,对调度结果中各最大资源量处的作业进行完全搜索,寻找较低资源用量的作业组合方式及执行方案,现就其中涉及的分支方法与支配规则进行阐述.
2.3.1分支方法 对所得作业位置列表,计算各时刻各资源消耗量,选择各资源最大用量处开始执行的j项作业进行深度搜索,通过回溯方法验证其邻域分支,直至完全搜索,具体步骤如下:
(2)确定j项作业中可以在节点g处执行的作业组合集合Cg;
(3)从Cg中随机选择作业组合Eg,更新Cg=Cg-Eg;
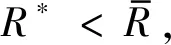
(5)若所有分支节点都满足Cg=∅,则搜索结束,更新原调度方案中j项作业的执行位置及资源消耗量.
以图3(a)所示7项作业的项目网络图为例,对应的搜索树结构如图5所示.图中:节点O=∅表示该时刻有未执行完成的作业,可以不选择新的作业执行.
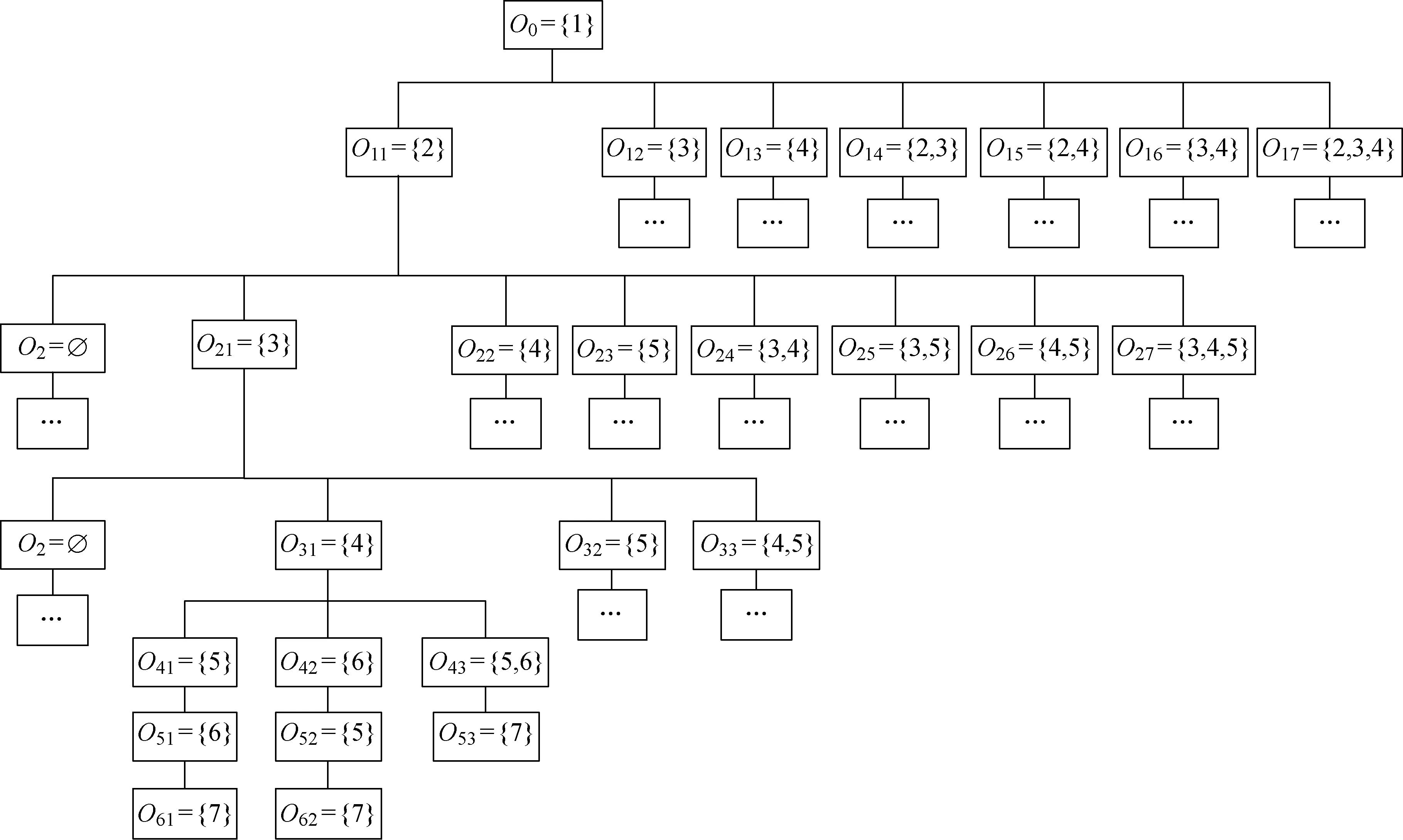
图5 搜索树示例Fig.5 Example of search tree
2.3.2支配规则 为提高分支过程搜索的效率,本文提出4种支配规则,用以剪除多余不可行或不好的分支.
定义当前调度时刻为t,当前节点为g,g在时刻t-1的根节点为g′,作业j:
(1)未调度且其紧前作业在t之前皆已执行完毕,则称作业j为时刻t可排作业;
(2)未调度且其tes=t,则称作业j为时刻t必排作业;
(3)已调度且其结束时间tft>t,则称作业j为时刻t执行作业;
(4)已调度且其结束时间tft≤t,则称作业j为时刻t已排作业;
(5)不属于已排作业,则称作业j为时刻t未排作业.
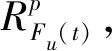
规则1若决策集E(t)中存在不包含所有必排作业集L(t)中的元素的子集Fv(t),v∈N*,则该子集Fv(t)所在节点不再分支.
证明所谓必排作业,即满足tls=t,tls的值是根据工期上限和资源空窗期确定的,代表作业的最晚开始时间,超出该时刻执行则表明项目一定会延期,在既定工期上限下无法求得可行解,所以对不包含必排作业的节点进行截断.
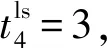
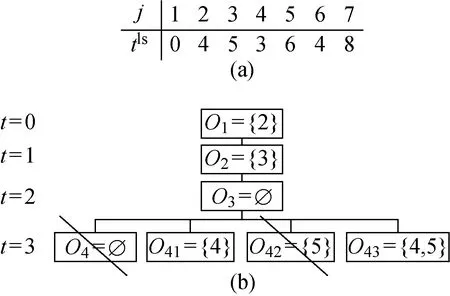
图6 规则1示例图Fig.6 Example of rule 1
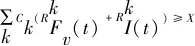
证明该问题旨在求得项目最低资源投入成本,当前已得可行解X,则任一资源用量不小于X的节点都无需再枚举.以图3(a)算例为例,示意图如图7所示.当前可行解X=7,该时刻已完成调度的作业为4(作业2未执行完毕),可排作业组合为{∅,{6},{3},{3,6}},各组合节点的资源使用成本分别为3/5/7/9,其中节点O22和O23的资源使用成本≥X,则相应节点被截断.
图7 规则2示例图Fig.7 Example of rule 2
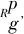
(14)
时刻t未排作业及子集Fv(t)中剩余未执行工期在[t+1,T]时间段内对各资源p的需求量

R=pg=(RpN(t)-RpFv(t))/(T-t-1)
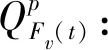
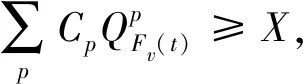

图8 规则3示例图Fig.8 Example of rule 3
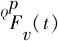
规则4若时刻t的决策集F(t)中存在2个子集Fu(t)和Fv(t)满足:
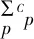
则子集Fu(t)所在节点不再分支.
证明2个子集Fu(t)和Fv(t)间存在从属关系,包含作业数多的子集Fv(t)在当前不完全调度下所得局部目标函数值明显优于包含作业数少的子集Fu(t),且不影响全局目标函数值,相对后续调度而言,Fv(t)能节省出更多资源及时间的选择,降低局部目标值提升的概率.
局部优化算法步骤如下:
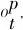
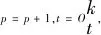
(3)根据支配规则判断当前节点是否能够剪除,若可以转步骤(4);否则,继续分支.
(4)若所有分支皆已枚举,则转步骤(5);否则,回溯搜索树,继续分支,转步骤(3).
(5)选择集合H的最优调度计划,更新原计划,若p>K,优化结束;否则,转步骤(2).
3 数值实验
为验证上述提出的带局部优化操作的遗传算法对于求解带资源空窗期的资源投入问题的有效性,本文运用C#(Visual Studio 2013)编程实现该算法,测试平台为Intel Core i5处理器,2.40 GHz主频,8 G内存.
3.1 实例验证
选取飞机装配过程中包含部分装配作业的一个小规模装配实例对所提算法进行验证分析.项目中共计18项作业,其中作业1和作业18为虚作业,工期为0且不占用资源.作业间时序关系、作业工期及所需资源量如表1所示.表中:资源R4存在空窗期 [0,1]和[27,29].分别利用CPLEX、本文提出的GA算法和文献[6]中设计的算法来求解该实例,调度方案如图9所示.图中:3种方法调度所得实例中的资源总成本分别为58、59和61.由于资源R4存在前后2段空窗期,限制了如2、4、15和17等作业的最早开始时间,导致其决策区间缩小,3种算法皆安排未使用资源4的作业3和作业16在相应空窗期时刻执行,降低空窗期前后位置的资源使用峰值.图9(b)和(c)中为本文设计的遗传算法求解该实例的结果,可以发现,当引入局部分支定界优化操作后能将资源量从63降至59,大大提升优化效率,甚至更优于文献设计的算法,获得接近于最优解的目标值.
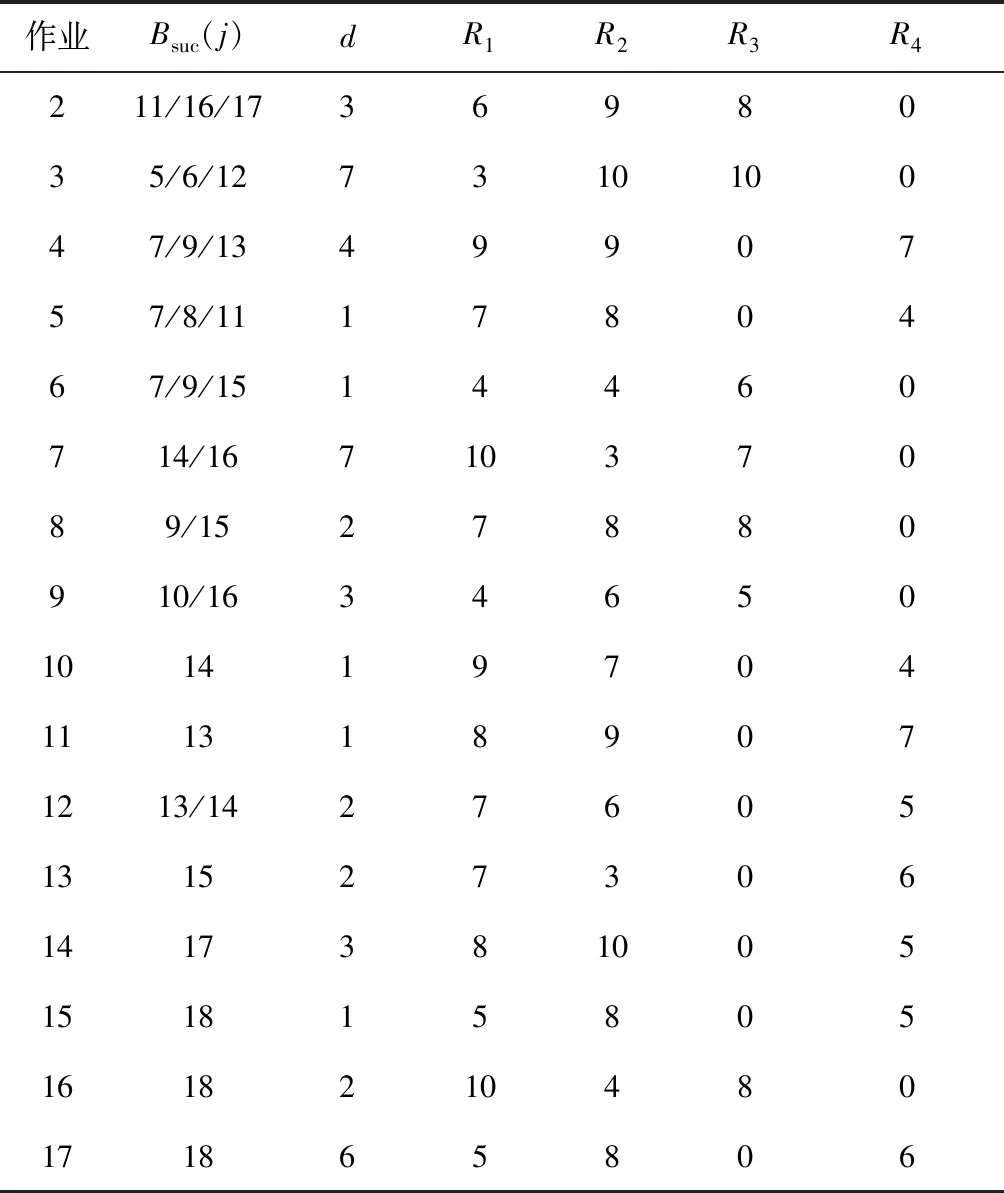
表1 作业时序关系、工期及资源量Tab.1 Precedence relations,duration and resources of jobs
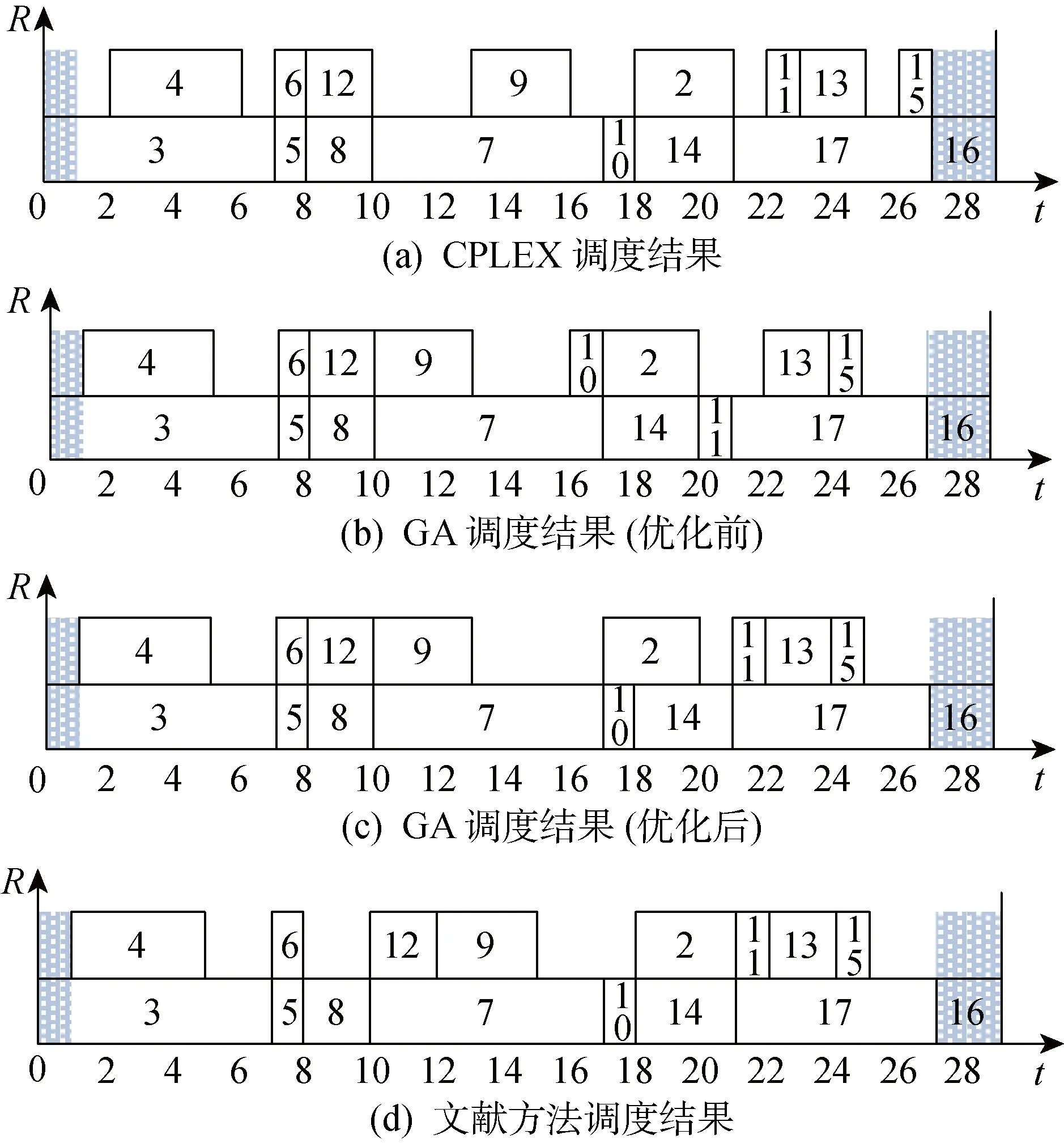
图9 各算法调度结果Fig.9 Scheduling results of different algorithms
3.2 算例对比分析
为了验证本文所提算法的有效性,将该算法的运行结果与CPLEX软件所求精确解及文献算法进行了对比.本文所用测试算例是基于测试问题库PSPLIB中的算例进行改造的,对于基本算例中未提供的参数,采用在一定大小范围内通过Random函数随机产生自然数的方式来确定,其中工期上限T取资源不受限下基于最早开始时间调度得到的作业最晚完成时间的 1.2 倍,资源空窗期通过在项目工期内随机产生长度为3的区间获得.
在表2~4中,每组包含5个算例,CPLEX列中OC表示CPLEX在处理本组5个算例时得到的最优解的平均值取整,tC表示CPLEX平均运算时间;GA列中AG表示本文算法在处理本组5个算例时得到的最好解的平均值取整,tG表示本文算法平均运算时间;对2种算法所得结果进行比较.BB列中AB表示本文局部优化算法中所设计的分支定界算法用以处理本组算例得到的最好解的平均值取整,tB表示算法平均运算时间,同样将其与CPLEX结果进行比较.其中:
从表2~4中GAP1项可以发现,对作业数为10,12,16的算例,本文所设计遗传算法求得的问题的解较CPLEX所得最优解分别相差 0.34%,0.78%,1.48%,平均偏差小于1%,从而证明本文算法在求解小规模问题上的有效性.表格中的后半部分,将应用于遗传算法中局部优化操作的分支定界算法用以求解相应算例,从BB栏的tB项及GAP2项可以发现,此算法能在较短的时间内获得问题的最优解,由此表明本文提出的4条支配规则能有效提高分支定界算法搜索效率.
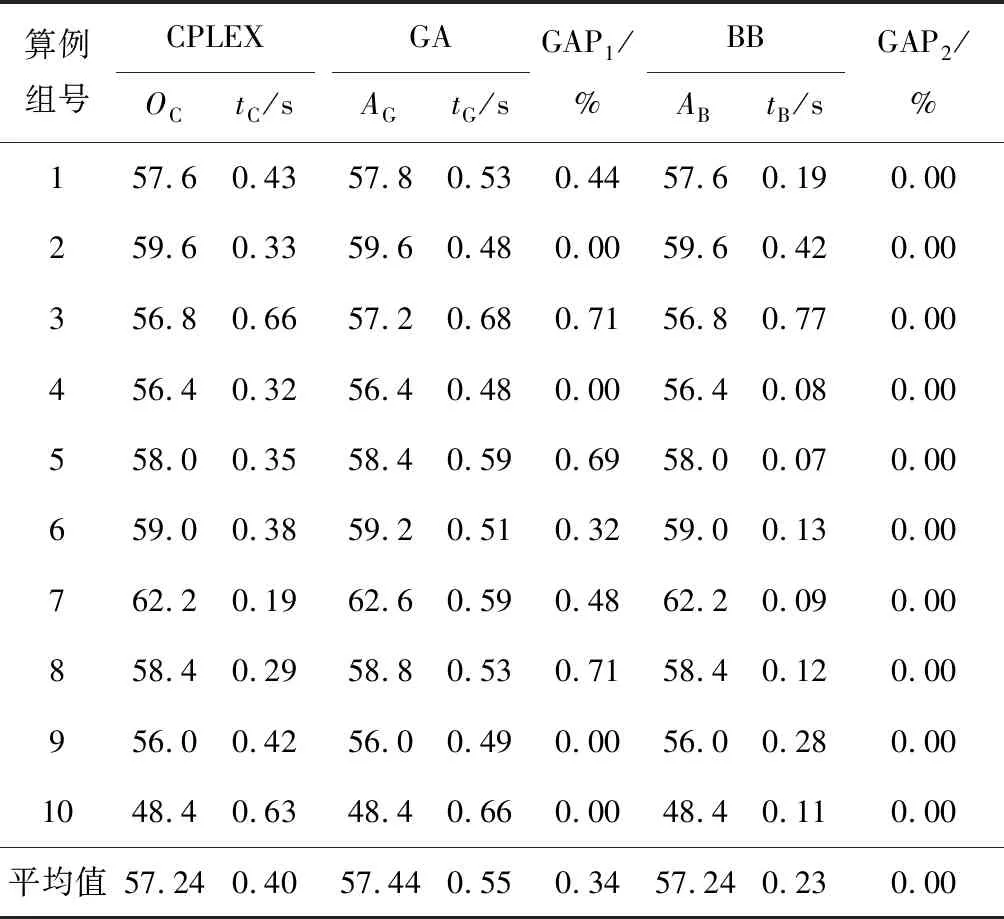
表2 10个作业实验结果Tab.2 Experiment results of 10 jobs

表3 12个作业实验结果Tab.3 Experiment results of 12 jobs
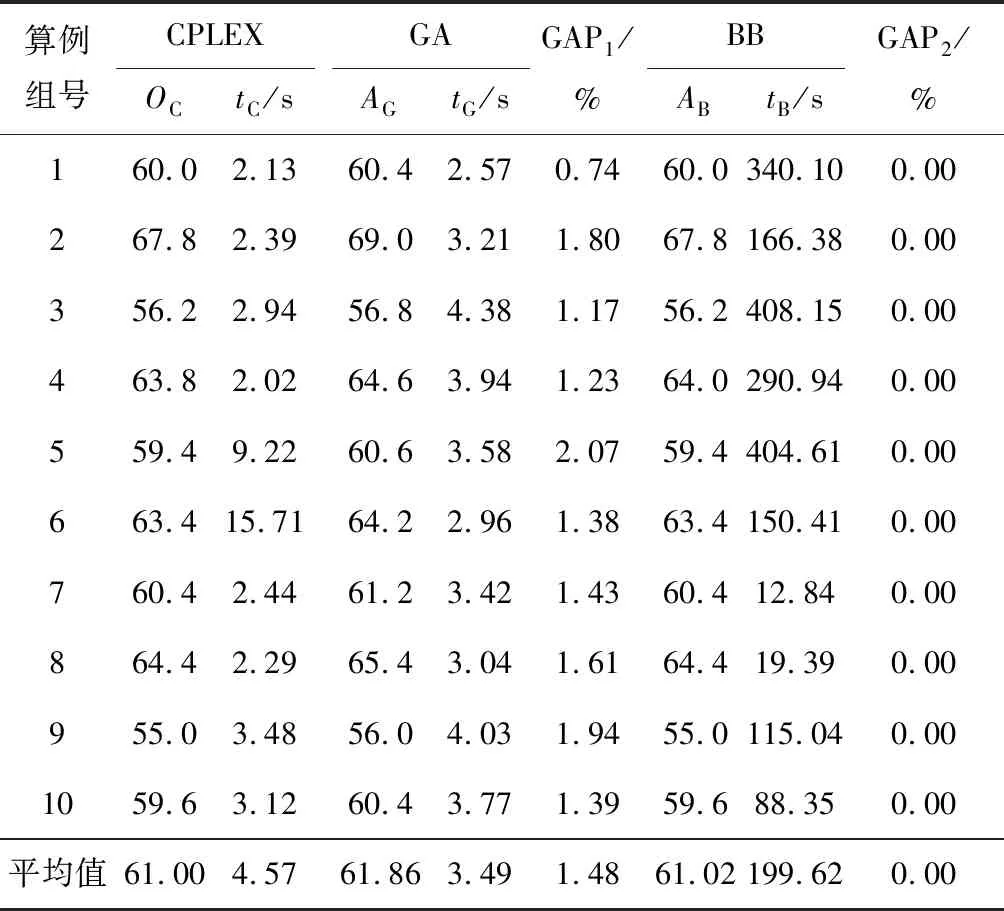
表4 16个作业实验结果Tab.4 Experiment results of 16 jobs
对于作业数为30,60,90的中大型规模的算例,CPLEX在规定时间内无法求得问题的最优解,所得上下界间的差距也极大,因此本研究中以此类规模算例为例,将所设计遗传算法与文献[6]中提出的人工免疫算法AIS进行了对比.表5~7中,每组同样包含5个算例,其中GA列中VG项表示GA在处理本组算例时运行5次后得到的最小值的平均值,tG项表示GA平均运算时间;AIS列中VA项表示对比算法在处理本组算例时运行5次后得到的最小值的平均值,tA项表示对比算法平均运算时间;
通过表5~7的数值结果可以发现,本文所设计的遗传算法较现有文献的人工免疫算法,就作业数为30,60,90这3类算例而言,求解精度分别提升1.96%,2.55%,3.36%,局部分支优化的操作能进一步降低所得资源成本,从而实现全局优化.
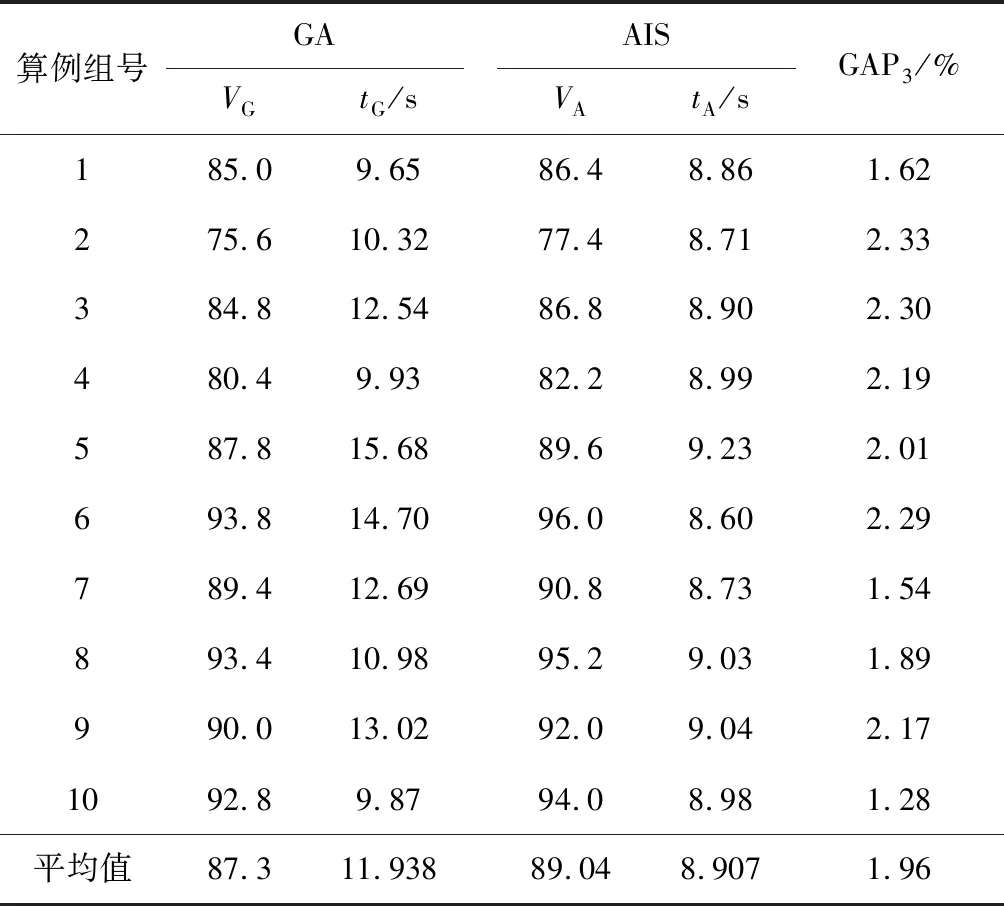
表5 30个作业实验结果Tab.5 Experiment results of 30 jobs
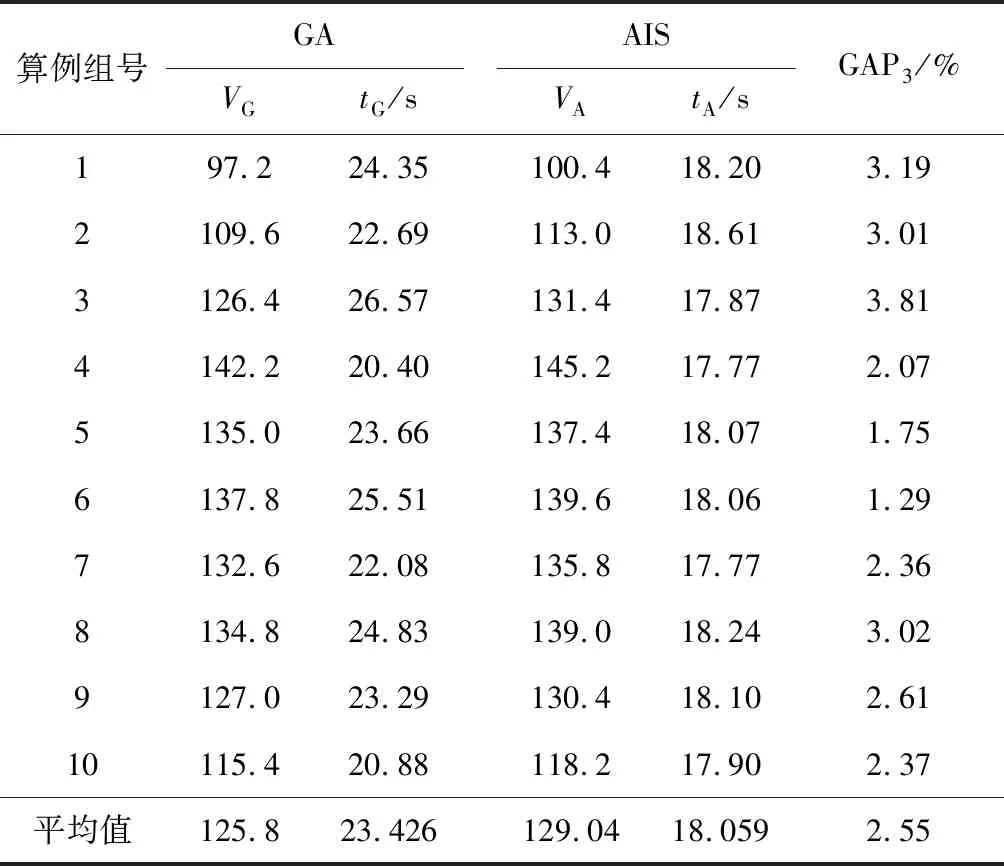
表6 60个作业实验结果Tab.6 Experiment results of 60 jobs
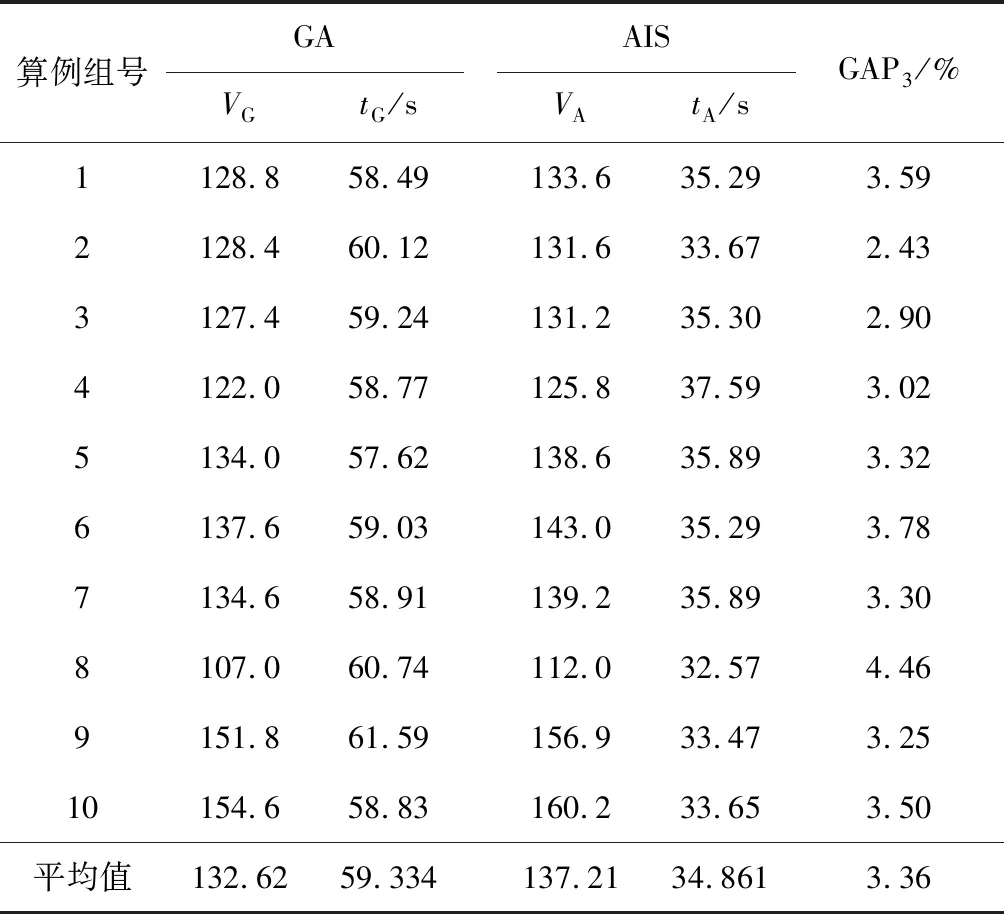
表7 90个作业实验结果Tab.7 Experiment results of 90 jobs
4 结语
资源投入问题是工程调度问题的一个重要分类,长期以来备受关注.针对飞机装配中部分关键资源存在空窗期这一特性,本文设计了带分支定界局部优化操作的改进型遗传算法求解该问题,提出了基于作业位置的编码方式,及在迭代中改进作业开始时间的变异机制.通过数值实验,验证了本文所提出的算法在求解该问题时的有效性.小规模算例中,算法所得解与最优解间的平均差值在1%以下;中大规模算例中,相较现有文献的人工免疫算法,带分支局部优化的遗传算法能进一步提升问题的求解精度,降低资源的投入成本.后续对该问题的研究中可以考虑引入作业可拆分、作业多执行模式等特性,通过降低空窗期对问题调度的影响,进一步优化调度结果.
