基于频分复用的无信号内干扰多用户相关延迟键控通信系统
2019-06-05徐联冰张天骐
张 刚,徐联冰,张天骐
(重庆邮电大学 通信与信息工程学院,重庆 400065)
混沌信号具有对初始条件敏感、非周期、类似于白噪声的宽频谱特性、良好的自相关和互相关性以及很强的抗噪声干扰能力等特性,可以在低信噪比和强干扰的环境中使用,因此被广泛用于高信息安全的通信领域[1-5].
混沌键控技术是混沌通信三大保密技术之一,其采用混沌扩频序列调制信息信号,具体方式有两种:相干解调[6]与非相干解调[7].相比于非相干解调,采用相干解调的混沌系统具有更好的误码性能,但需要用到混沌同步技术来解调接收信号.由于混沌同步技术实现起来比较困难,所以近几年来,基于非相干解调的差分混沌移位键控[8](Differential Chaos Shift Keying,DCSK)和相关延迟键控[9](Correlation Delay Shift Keying,CDSK)方案成为研究者热点关注的话题[10-11].然而,由于调制信息的过程中会引入更多的信号间干扰,CDSK的误码性能远差于相干混沌系统.尽管DCSK通过传输-参考模式克服了相干解调过程中出现的门限漂移问题并提高了系统的误码性能,但DCSK的安全性能比CDSK更差,因此窃听者很容易截取到传输的信息[12-13].
针对DCSK系统,研究者提出了一些改进方案.文献[14]提出了一种基于频分复用的高效差分混沌移位键控(FDM-HEDCSK)系统.该系统将两个混沌信号的简单加、减法线性组合作为参考信号调制对应的四比特信息信号,并通过频分复用的方式发送每一路信号,因此有效地提高了带宽效率和误码性能.此外,该系统通过利用两个混沌信号发生器发送四比特信息信号,提高了系统的安全性.文献[15]提出了一种基于正交混沌载波的多用户差分混沌移位键控(OMU-DCSK)系统.该系统利用正交混沌信号发生器产生一组互相正交的混沌序列,有效降低了系统平均比特能量并完全消除多址干扰,以牺牲较小复杂度的代价有效提高了系统的误码性能.文献[16]提出了一种无信号内干扰高效差分混沌移位键控(HE-DCSK)系统.该系统通过设计一个正交混沌信号发生器,确保产生两路严格正交的混沌信号来分别调制信息信号,彻底消除了解调时产生的信号内干扰分量,从而有效地提高了系统的误码性能.
针对DCSK系统及其改进的方案都不能同时提高误码性能和传输速率的问题,本文提出一种基于FDM的NISI-MU-CDSK(Multiple User Correlation Delay Shift Keying with No Intra-Signal Interference,NISI-MU-CDSK)通信系统.该系统利用正交混沌信号发生器产生两路正交的混沌信号,并将混沌信号进行简单加、减法线性组合,并与其调制的信息信号通过FDM 实现传输,使得系统接收端解调时不会产生信号内干扰,从而达到提高误码性能的效果.文中将NISI-MU-CDSK在AWGN信道和Rayleigh衰落信道下的Monte Carlo仿真实验与理论推导进行对比,结果表明:该系统的Monte Carlo仿真实验和理论推导基本相符,且误码性能和传输速率得到提高,具有一定的研究前景.
1 NISI-MU-CDSK系统原理
为避免接收端产生信号内干扰分量,引用一个正交混沌信号发生器[16]产生两路严格正交的混沌载波信号,如图1所示.图中:β为扩频因子;xi,k,yi,k为正交混沌信号发生器的输出.在前β/2时隙内,输出信号xi,k和yi,k相同;在后β/2时隙内,输出信号xi,k和yi,k相反,以保证输出信号xi,k和yi,k在一个β时隙内严格正交.正交混沌信号发生器的输出满足以下关系:
(1)
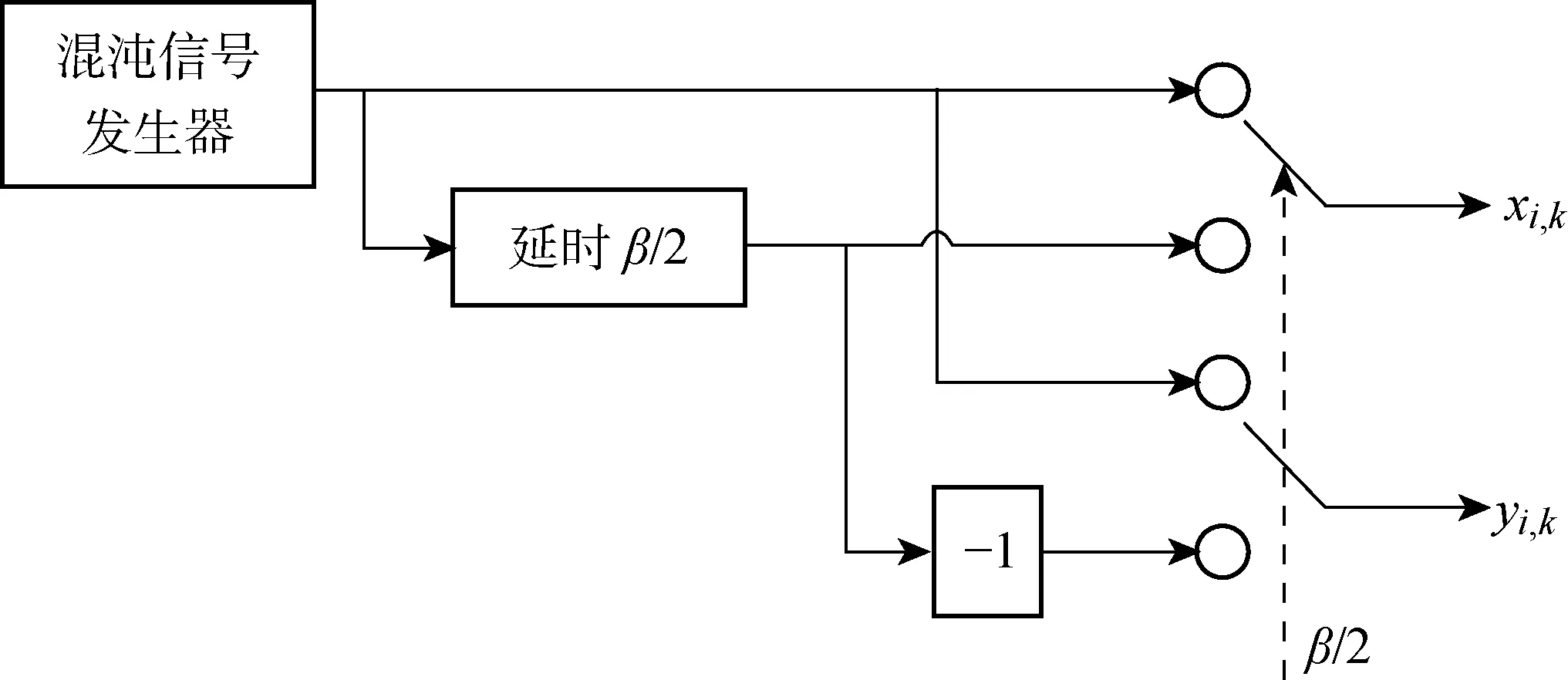
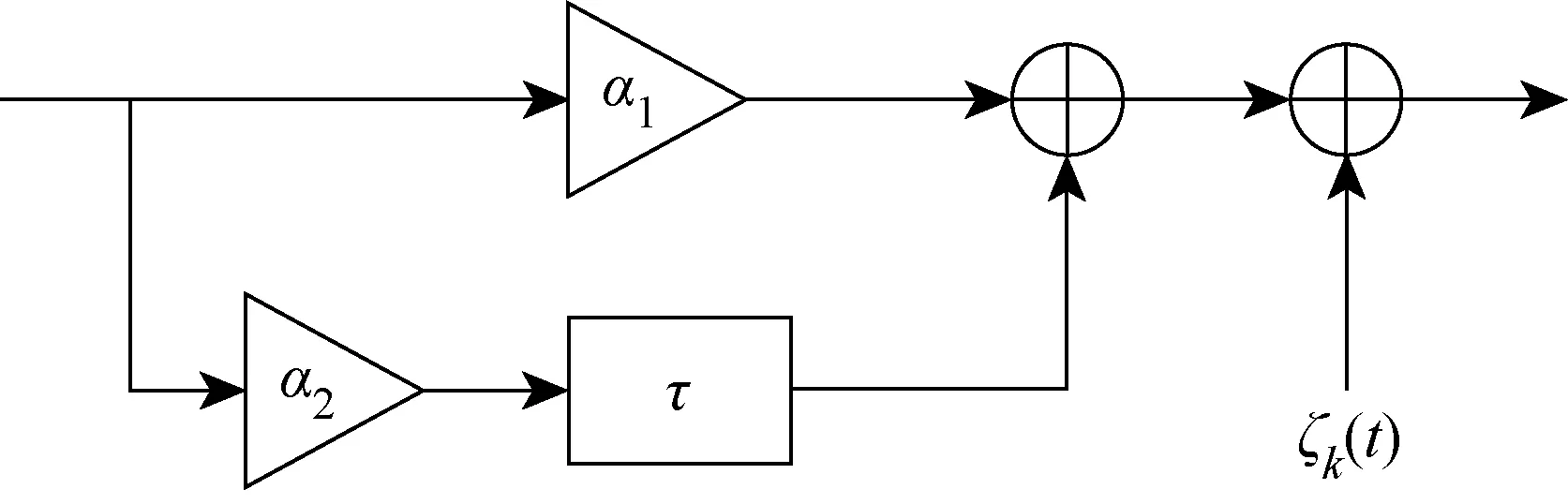
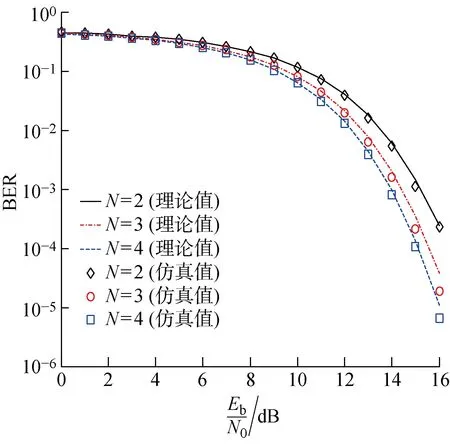
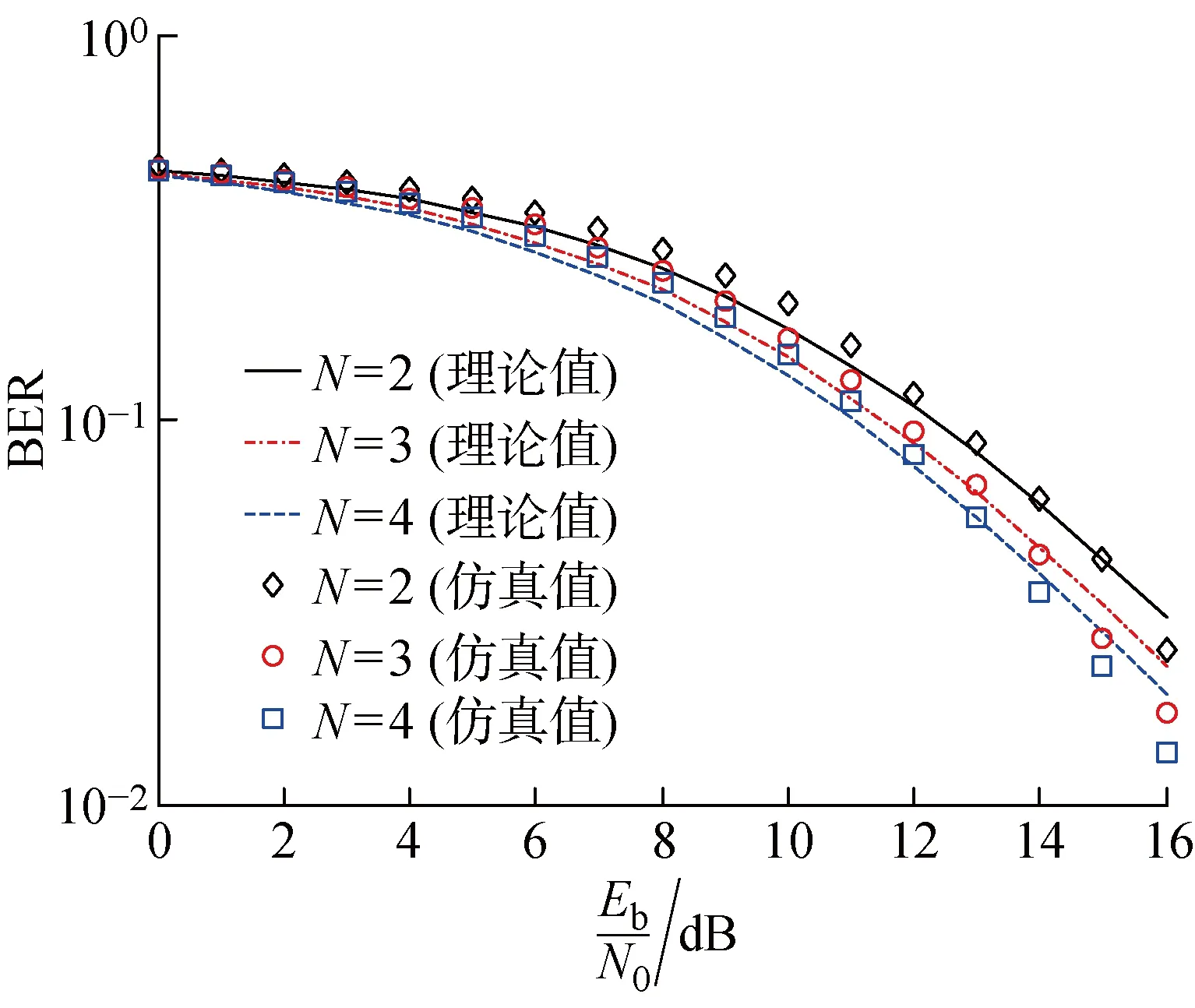
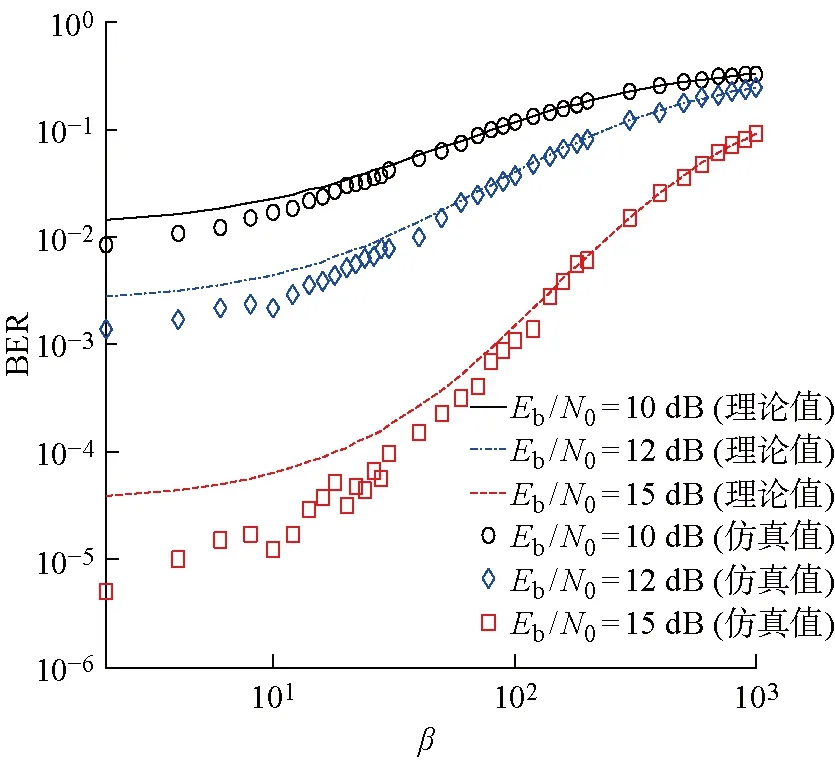
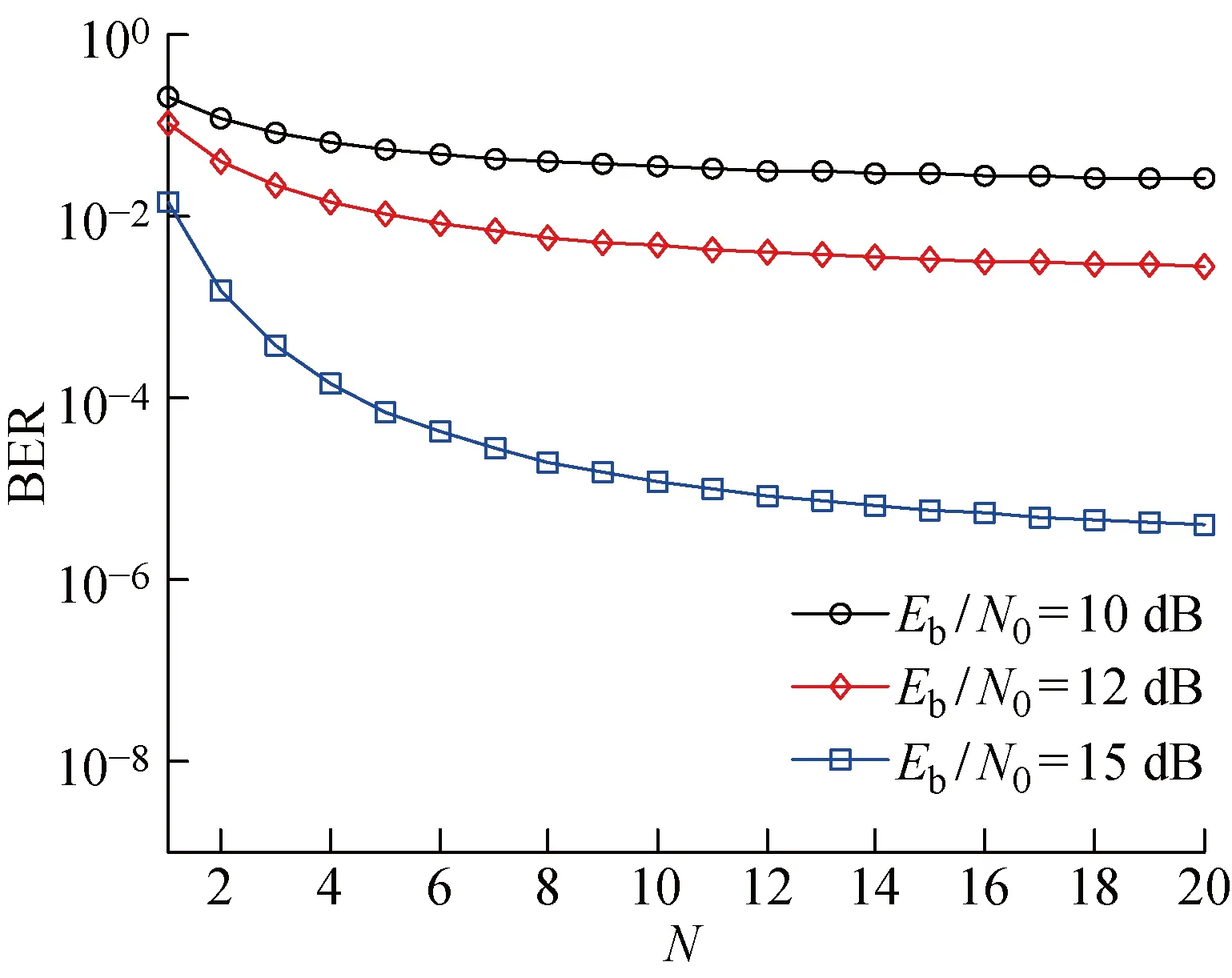
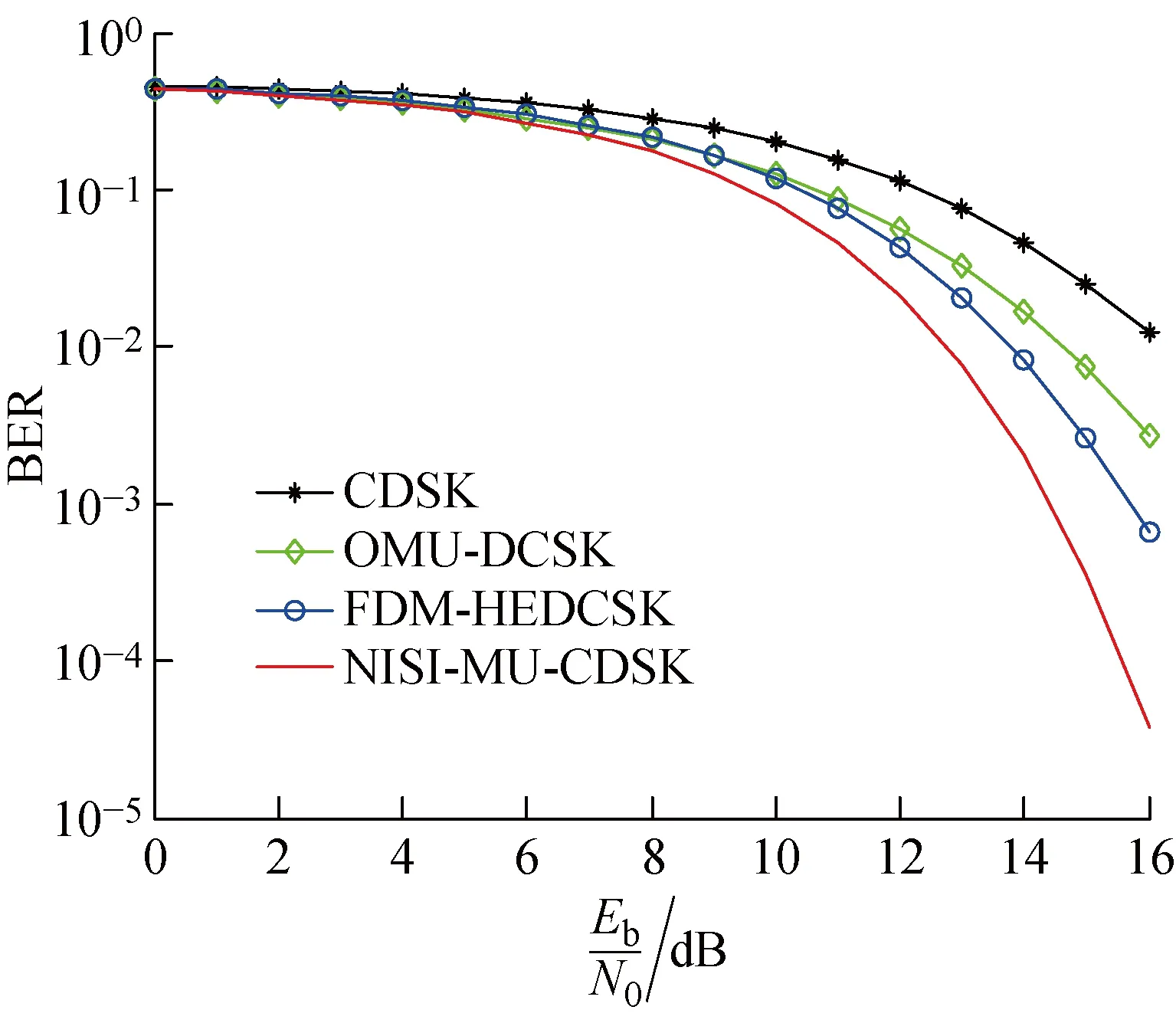
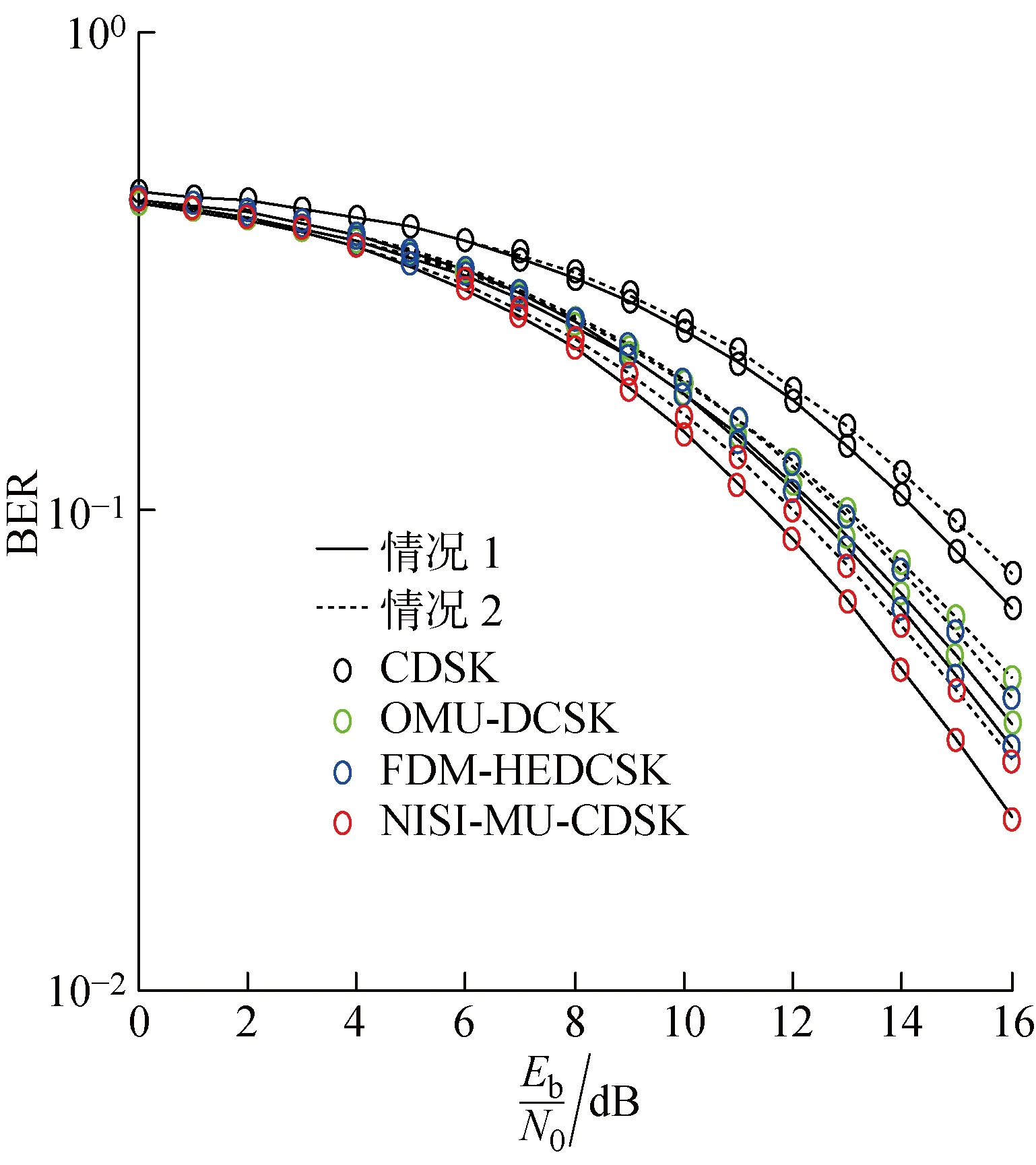
kβ (2) k,m=0,1,… 式中:i=1,2,…,β;xi,k和yi-mβ,k为正交混沌信号发生器第k帧的输出项,m的取值决定yi-mβ,k所处的时隙. FDM使用不同频率发送各路数据信息以实现多路通信,其优点是信道复用率高、分路方便,因此在目前的通信系统中被广泛使用[14].本文提出一种基于FDM的NISI-MU-CDSK系统,假设系统每帧传输2N个用户,发送第k帧信息信号的发送端框图如图2所示. 图1 正交混沌信号发生器Fig.1 Orthogonal chaos signal generator 图2 NISI-MU-CDSK系统发送端框图Fig.2 Transmitter block diagram of the NISI-MU-CDSK (3) (4) xi,k∈{-1,+1} yi,k∈{-1,+1} E[xi,k]=0 var[xi,k]=1 E[yi,k]=0 var[yi,k]=1 其中:E[·]表示均值;var[·]表示方差;比特能量恒定. (5) 此时发送端发送信号的平均比特能量为 (6) 图3 NISI-MU-CDSK系统接收端框图Fig.3 Receiver block diagram of the NISI-MU-CDSK 在实际应用中,信号在空间传输时反射和折射会消耗信号能量,导致接收到信号的幅度、相位和时延会改变,因此本文研究NISI-MU-CDSK系统在Rayleigh衰落信道中的误码性能.为研究方便,推导了NISI-MU-CDSK在两径Rayleigh衰落信道中的比特误码率(BER)公式.图4所示为两条独立路径的Rayleigh衰落信道.图中:α1和α2为服从Rayleigh分布的相互独立的衰落系数;τ为两条独立路径之间的时间延迟;ζk(t)为满足一阶矩为零、二阶矩为N0/2的加性高斯白噪声.文中假设τ远小于符号间隔,即τ≪β,所以符号间干扰远小于多径干扰,可以忽略不计.本文讨论两径Rayleigh衰落信道中增益的两种常见情况. 情况1两条路径的平均能量增益均为 0.5,即 情况2两条路径的平均能量增益相差6 dB,即 则在第k帧,NISI-MU-CDSK系统接收端接收到的信号为 rk(t)=α1sk(t)+α2sk(t-τ)+ζk(t) (7) 图4 两径Rayleigh衰落信道结构Fig.4 Two-path Rayleigh fading channel structure 每一路低通滤波器的输出为 (8) (9) α2b(k-1)N+jxk(t-τ)+ (10) 每一路采样后的信号可表示为 (11) (12) (13) 在接收端,解调第j个用户的信息输出为 Zj=Rj+Rj+N= (α1b(k-1)N+jxi,k+α1bkN+jyi,k+α2b(k-1)N+jxi-τ,k+ (14) (α1b(k-1)N+jxi,k+α1bkN+jyi,k+α2b(k-1)N+jxi-τ,k+ 式中:A为有用信号项;B为信号与噪声间的干扰项;C为噪声间的干扰项.通过对比本文相关解调输出表达式(14)与文献[18]中推导的传统通信系统 CDSK 的相关解调输出可以发现,CDSK系统的相关解调输出有12项为信号间干扰项,而本文提出的系统完全消除了信号间干扰项.一方面,在发送端构造两路混沌信号的加、减法的线性组合作为参考信号,在接收端将相关器对应的输出进行对应的加、减法的线性组合,并通过FDM技术传输多用户信息.以上操作消除了用户间干扰,使得最终输出表达式的相关项减少,从而减少了部分信号间干扰项.另一方面,通过在发送端使用正交混沌信号发生器确保产生的两路混沌信号xi,k和yi,k严格正交,使得式 (14)的信号间干扰项(2α1xi,k+2α2xi-τ,k)(α1bkN+jyi,k+α2bkN+jyi-τ,k)为零,从而彻底消除了所提系统的信号间干扰分量.此外,由于本文采用的是Logistic映射,其自相关旁瓣为零,则有 (15) 同理可得解调第j+N个用户的信息输出为 Zj+N=Rj-Rj+N= (α1b(k-1)N+jxi,k+α1bkN+jyi,k+α2b(k-1)N+jxi-τ,k+ (16) (α1b(k-1)N+jxi,k+α1bkN+jyi,k+α2b(k-1)N+jxi-τ,k+ 本文采用高斯近似法(Gaussian Approximation,GA)分析并推导NISI-MU-CDSK在 Rayleigh衰落信道下的BER公式.GA法在β取较大的值时能准确地分析系统的性能.根据中心极限定理可得 E[Zj]=E[A]+E[B]+E[C]= (17) (18) 则可得NISI-MU-CDSK在两径Rayleigh衰落信道下的BER为 (19) 式中:erfc(·)为互补误差函数, 令 γb=γ1+γ2 则式(19)可进一步简化为 (20) 令 则γ1和γ2服从卡方分布: (21) γb服从以下分布: (22) 因此,由式(20)和(22)得到NISI-MU-CDSK系统在两径Rayleigh衰落信道下的BER公式为 (23) 观察式(23)可知,在Rayleigh衰落信道中影响NISI-MU-CDSK系统BER的因素除了N、β以及信噪比Eb/N0外,还有α1和α2. 在式(19)中,令α1=1,α2=0,则可得NISI-MU-CDSK系统在AWGN信道中的BER为 (24) 由于实际信息传输中出现误码的情况是不可避免的,所以误码率的研究尤为重要.式(23)与(24)分别描述了NISI-MU-CDSK系统在Rayleigh衰落信道和AWGN信道下的误码性能表达式,其物理意义为当要发送的信息比特为“0”(或者“1”),而通过接收端解调出的信息比特为“1”(或者“0”)时,系统传输该信息比特时发生错误.而BER是用来描述一个系统在传输信息比特过程中出现误码的概率,所以BER是评价系统性能的重要指标. 根据文献[14]、[15]和[18]可知,使用具有相同均值和方差的映射也可推导出CDSK、FDM-HEDCSK以及OMU-DCSK的BER公式: (25) (26) (27) 对比式(24)与(25)可知,N增加时,系统的BER减小,即当N=1时,系统的BER最大,此时系统的BER明显小于CDSK系统的BER,所以本文所提系统的误码性能始终优于CDSK系统.同样对比式(24),(26)和(27)可知,当N大于某个临界值时,本文所提系统的误码性能优于OMU-DCSK 和FDM-HEDCSK系统,具体性能比较在下一节中体现. 本节对NISI-MU-CDSK系统在AWGN信道和Rayleigh衰落信道下的BER进行Monte Carlo仿真实验并与理论推导进行对比;研究NISI-MU-CDSK性能与N、β和Eb/N0的关系,同时与传统CDSK、OMU-DCSK以及FDM-HEDCSK的BER进行仿真对比分析.仿真采用Logistic映射,仿真曲线为106次Monte Carlo仿真的结果. 图5 AWGN信道中不同用户数BER变化曲线Fig.5 The BER performance curves with different users in AWGN channel 图6 Rayleigh信道中不同用户数BER变化曲线Fig.6 The BER performance curves with different users in Rayleigh channel 图5和6分别为NISI-MU-CDSK系统在N=2,3,4时,AWGN信道和Rayleigh衰落信道下BER随Eb/N0变化的曲线.其中仿真时β取值为100,Rayleigh衰落信道的增益均为 0.5.从图5和6可以看出,Monte Carlo仿真的BER结果(用“仿真值”表示)和理论推导的BER结果(用“理论值”表示)大致相符.当N一定时,系统BER随Eb/N0的增大而减小;当Eb/N0一定时,系统BER随N的增大而减小.这是因为N的增加可以有效地降低系统平均比特能量,并且NISI-MU-CDSK系统彻底消除了信号间干扰项. 图7和图8分别为NISI-MU-CDSK系统在AWGN信道下Eb/N0为10、12和15 dB时BER随β和N变化的曲线.仿真时其余参数取值为图7中N=2,图8中β=100.从图7中可以看出,当Eb/N0一定时,系统BER随β的增大而增大,且只有当β较大时BER的仿真值与理论值基本吻合.这是由于当β较小时,接收端的判决变量不再满足高斯分布,进一步验证了理论推导的正确性.从图8中可以看出,当Eb/N0一定时,系统BER随N的增大而减小,当N接近20时,系统BER趋近于稳定.从式(32)中也可以看出,随着N的增加,系统的BER趋近于一个固定值. 图7 系统误码率随扩频因子变化曲线Fig.7 The system BER curve with different spreading factor β 图8 系统误码率随用户数变化曲线Fig.8 The system BER curve with different users N 图9 AWGN信道中NISI-MU-CDSK与其它系统BER比较曲线Fig.9 The BER performance curve of NISI-MU-CDSK compared to other systems in AWGN channel 图10 Rayleigh信道中NISI-MU-CDSK与其它系统BER比较曲线Fig.10 The BER performance curve of NISI-MU-CDSK compared to other systems in Rayleigh channel 图9和10分别为NISI-MU-CDSK系统在AWGN信道和Rayleigh衰落信道下BER与CDSK、OMU-DCSK和FDM-HEDCSK系统的BER比较曲线.其中仿真时其余参数取值N=3,β=100.可以看出,NISI-MU-CDSK的BER远小于CDSK、OMU-DCSK和FDM-HEDCSK系统的BER,其原因有3个方面.首先,NISI-MU-CDSK系统在发送端构造两路混沌信号的加、减法线性组合以及接收端构造对应的线性组合可减少信号间干扰项.其次,在发送端使用正交混沌信号发生器使得系统在接收端进行相关解调时能消除信号间干扰.另外,通过FDM技术传输多用户信息消除用户间干扰,可提升系统的误码性能.从图10中还可以看出,系统在两条路径平均能量增益不同时的误码性能比两条路径平均能量增益相同时的误码性能差. 本文在传统CDSK系统的基础上提出了一种基于FDM的NISI-MU-CDSK混沌通信系统.该系统通过FDM方式传输多用户信息,并引入正交混沌信号发生器,在发送端构造两路混沌信号的加、减法线性组合,能彻底消除信号间干扰,可提高系统的误码性能.通过GA法推导了NISI-MU-CDSK系统在Rayleigh衰落信道下的BER公式并进行了Monte Carlo 仿真.结果表明:本文所提系统的误码性能较CDSK有很大提高,甚至优于OMU-DCSK以及FDM-HEDCSK系统,具有较好的研究意义和应用价值.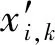




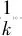
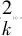
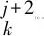
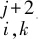
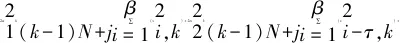
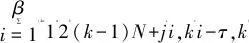
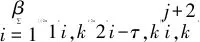
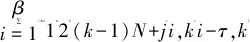
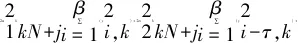
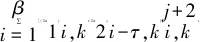

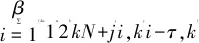
2 NISI-MU-CDSK系统性能分析
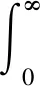
3 仿真分析
4 结语
