基于改进反馈判决的自动识别系统信号解调算法

唐 然，赵迎新，吴 虹

(南开大学 电子信息与光学工程学院,天津 300350)

自动识别系统(AIS)是一种信息交换系统，船载AIS设备不断发送自身信息，如航向、吨位等，用以领航调度，避免碰撞.随着海运贸易的高速增长，迫切需要建立对大片海域船舶动态的实时监控系统.卫星平台因覆盖范围广而受到重视，加拿大等国家相继发射载有AIS信号接收设备的卫星[1].AIS采用高斯滤波最小频移键控(GMSK)调制，可以通过相干方式或非相干方式解调.相干解调具有较好的抗噪声性能[2-3]，但是需要准确恢复载波，而载有AIS设备的近地卫星轨道高度一般在500 km左右，多普勒频移可达±4 kHz，且AIS采用自组织时分多址(SOTDMA)技术，每个用户工作时隙时间较短，无法采用锁相环等闭环方式实现精准载波恢复；非相干解调(主要是采用鉴频器)具有对频偏不敏感且结构简单的优点，在很多GMSK移动通信系统中得到了应用[4-6].另外，由于GMSK基带信号采用高斯滤波器实现脉冲成型，通过引入码间干扰(ISI)来获得高频谱效率，因此会牺牲一定的误码性能.目前已经有很多学者提出克服ISI的方法，如Viterbi检测[7-9]，反馈判决[10-11]等.考虑到星载设备需要进行三模冗余设计[12]，因此选择的算法复杂度不宜过高，反馈判决则是一种比较理想的选择.

由于非相干解调对噪声比较敏感，因此在非相干解调器前后通常分别增加预检测滤波器和后检测滤波器来抑制带外噪声.预检测滤波器的截止频率需要留出一部分裕度，以应对多普勒频偏导致的接收信号中心频率的偏移.而后检测滤波器的带宽通常选择尽量小，以充分抑制鉴频器输出的尖峰脉冲噪声.而过小的带宽可能导致鉴频器输出的有用信号被抑制，形成畸变.这种畸变会使解调出的基带码元的眼图压缩，造成误码性能降低.例如，文献[10，13]中的后检测滤波器采用高斯低通滤波器，其3 dB带宽在 0.45Rb(Rb为GMSK调制信号的比特速率)附近，而由比特信息[-1,1,-1]或[1,-1,1]产生的GMSK基带信号的最高跳变频率为 0.5Rb，大于 0.45Rb，因此也会受到抑制而引起失真.目前，国内外尚无相关文献对后检测滤波引起失真的问题进行分析.本文主要分析了鉴频器输出信号畸变和后检测滤波器的关系，并通过调整判决反馈算法中的反馈电平来补偿这种畸变，以提高误码性能；利用AIS帧头的位同步信号和起始标志来获得反馈电平和判决门限，消除多普勒频偏以及其他因素对反馈判决的影响.仿真表明，这种改进的反馈判决方法和后检测滤波器结合使用时，可以显著提高GMSK系统的误码性能，在信噪比(SNR)为 4.5 dB时误码率(BER)降到10-5，满足AIS标准的误码要求.

1 GMSK信号调制解调原理和反馈判决算法

1.1 GMSK调制解调原理

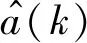
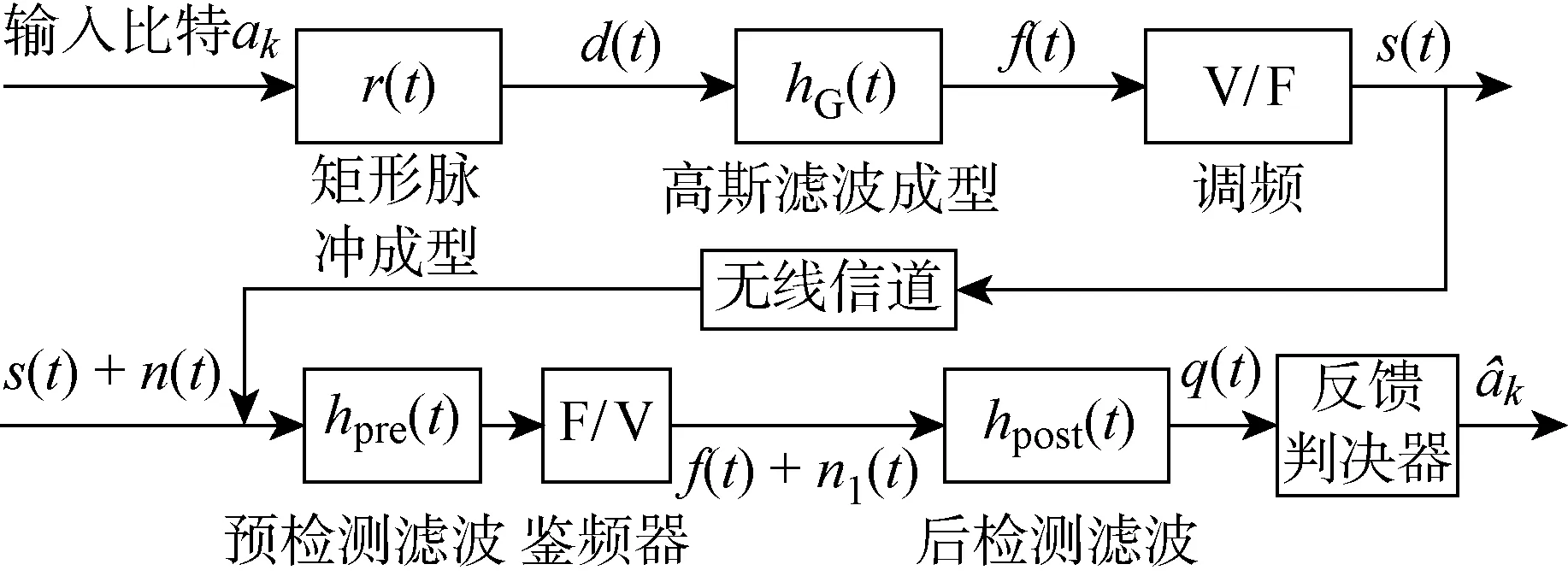
图1 GMSK调制和非相干解调原理Fig.1 Block diagram of GMSK modulation and non-coherent demodulation

发射端比特脉冲为

(1)

式中：ak=±1为比特信息；Tb为比特周期；r(t)为矩形脉冲信号，

(2)

比特脉冲d(t)通过带宽时间积(BT)为BbTb的高斯滤波器进行脉冲成型，Bb为发射端高斯滤波器的3 dB带宽.BT值越小意味着频谱效率越高，同时引入的ISI也越大.高斯成型滤波器的冲激响应为

(3)

滤波成型后的信号为

(4)

式中：*表示卷积运算；

g(t)=r(t)*hG(t)=

(5)

erf()为误差函数.最后通过电压/频率(V/F)转换，形成调频信号并调制到规定频段发射出去.

非相干解调的接收机首先是将接收信号进行正交下变频，然后滤除高频分量和带外噪声后得到基带信号I(t)和Q(t)，再通过下式进行频率/电压(F/V)转换.即

(6)

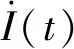
(7)

设Ts为数字信号采样频率，则

(8)

1.2 传统的反馈判决方法

本文的改进是基于文献[10]中提出的反馈判决方法.假设ISI是由相邻两比特信号造成的，那么在第k个码元采样时刻，GMSK的基带电平可表示为

(9)

接收端在第k个码元采样时刻，通过减去k-1时刻比特信号的干扰来降低ISI，干扰值为

(10)

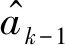
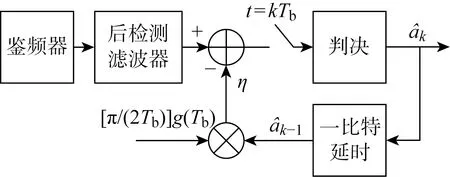
图2 传统反馈判决法原理图Fig.2 Block diagram of traditional decision feedback method

2 后检测滤波器失真和改进的反馈判决算法

2.1 后检测滤波器失真效应

由于鉴频器对噪声十分敏感，因此GMSK信号进行鉴频之前需要经过预滤波来滤除带外噪声，鉴频器输出信号也需要后检测滤波器来滤除由噪声引起的高频尖峰脉冲.通常后检测滤波器的截止频率要尽量小，以达到充分抑制噪声的目的.但是，截止频率太小同样会抑制鉴频器输出的有用信号成分，造成有用信号失真，降低误码性能.因此，在选择后检测滤波器截止频率时需要权衡.图3(a)是AIS一帧中的起始比特信息对应的GMSK基带波形，这些脉冲信号已经过高斯成型滤波；图3 (b)是信噪比为8 dB时，接收端鉴频器解调出的基带信号，可以看出叠加了尖峰脉冲噪声；图3(c)是鉴频器输出信号经过带宽为 0.4Rb的高斯后检测滤波后的输出.由图可见，虽然尖峰脉冲噪声被有效滤除了，但是跳变频率高的部分也受到了抑制，引起了失真.图4所示为发射端基带信号和接收端后检测滤波输出的基带信号眼图的对比.由图可见，这种失真会使眼图张开程度缩小，从而降低误码性能.

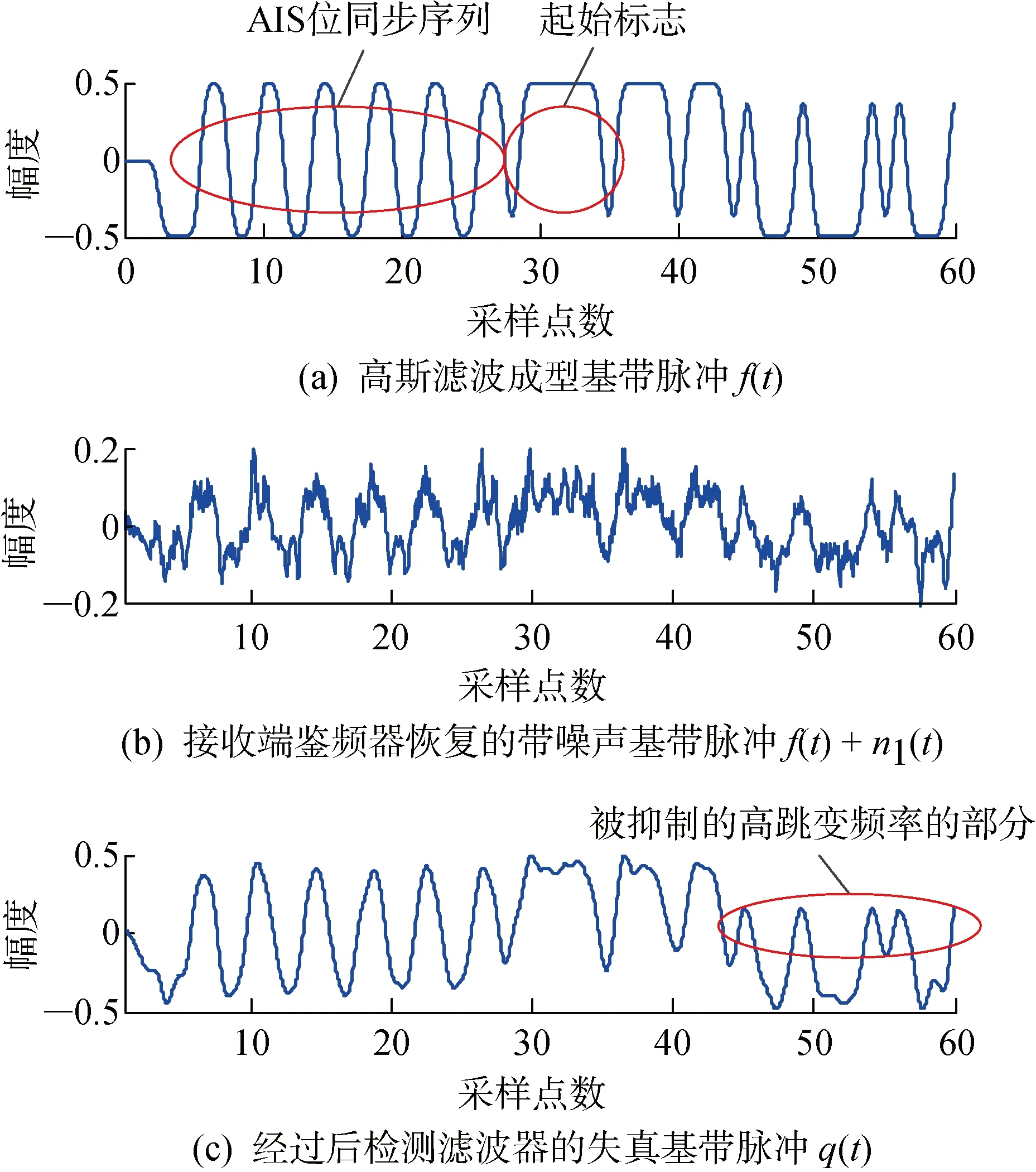
图3 后检测滤波器引起的失真示意图Fig.3 Illustration of distortion caused by postdetection filter

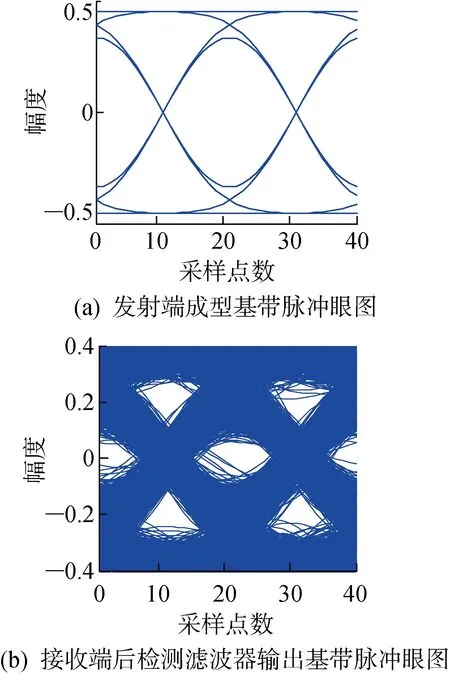
图4 发射端和接收端基带波形的眼图对比Fig.4 Comparison of eye diagrams for transmitted and received baseband pulse

2.2 改进的反馈判决方法

为了分析2.1节中的失真效应和后检测滤波器的关系，假设接收到的信号不含任何噪声，那么鉴频器的输出应当等于f(t)，则后检测滤波器的输出为

(11)

式中：hpost(t)为后检测滤波器的冲激响应.假设接收端后检测滤波器也采用高斯低通滤波器[10,13]，其3 dB带宽为Bo，即

(12)

因此

hG(t)*hpost(t)=

F-1[HG(f)Hpost(f)]=

(13)

式中：F-1[]为傅里叶逆变换；HG(f)和Hpost(f)分别为hG(t)和hpost(t)的频率响应；

(14)

对照式(13)、(11)和式(3)、(4)，可得后检测滤波输出为

(15)

式中：g1()为通过将式(5)中g()中的Bb替换成B1后得到的函数.类比2.1节中的推导，可以得到后检测滤波输出在第k个码元采样时刻的幅度为

(16)

因此，得到修正的反馈电平为

(17)

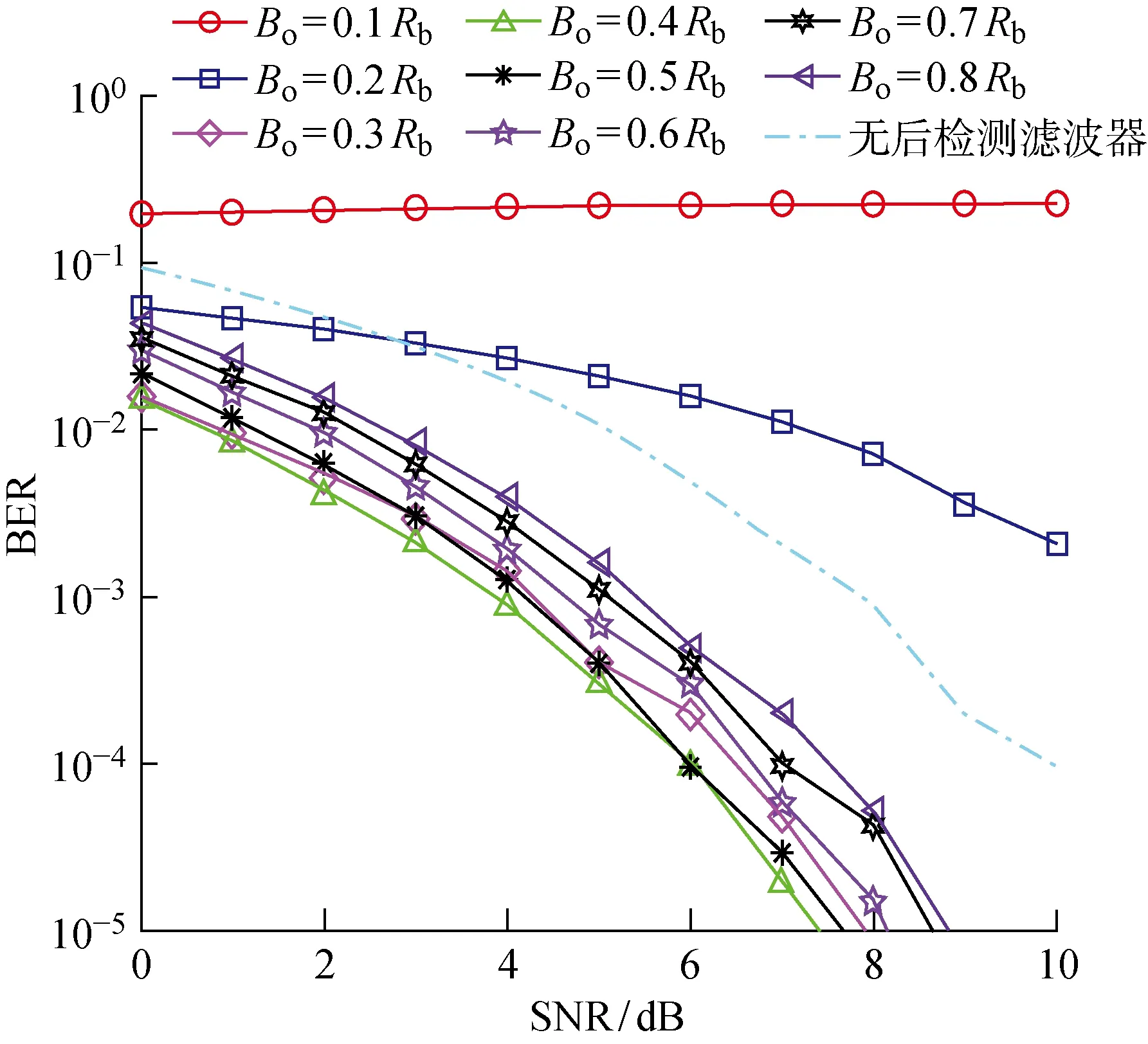
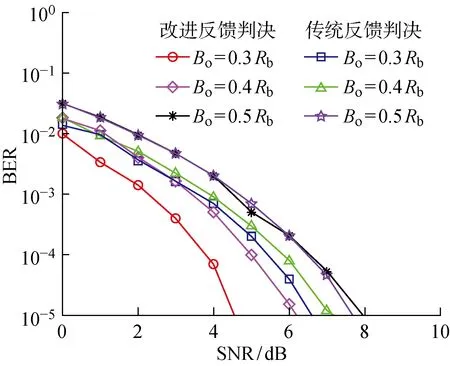
上述失真分析的实质，是忽略了从高斯成型滤波到后检测滤波器之间的所有过程，从而可以将此两者级联并等效成一个3 dB带宽为B1的高斯滤波器，如式(13)所示.根据式(14)可以发现，B1

2.3 AIS判决反馈模块中反馈电平的计算

如式(17)所示，在AIS接收机中应用反馈判决需要计算g1(Tb)的值，在实际的AIS软件接收机中，鉴频器是数字式的，如式(7)和(8)所示，其输出取决于输入信号的实际频率(可能包含多普勒频偏)和采样频率，以及硬件系统中其它会对信号幅度产生缩放的因素，如后检测滤波、浮点参数设置和数据截位等.假设硬件中的信号电平和理论值成正比例，比例系数为c，则式(17)中的反馈电平在硬件系统中的实际值为

η=cη1

(18)

本文根据AIS帧头的位同步和起始标志来计算实际反馈电平值.AIS协议中规定，每帧信号256比特数据，帧头包含24比特11001100…1100的位同步序列，以及01111110的起始标志，如图3(a)所示.当AIS接收机通过相关检测到位同步序列，并实现位同步时，对位同步序列部分的鉴频输出取平均值，可以得到一个判决门限δ，它和系统的频偏是对应的，即

δ=cΔω

(19)

式中：Δω为系统频偏，包括多普勒频移，本振偏移等.再通过判决找到起始标志01111110.将起始标志中连1的部分取平均值记为ξ，并假设只有相邻比特会对当前信号产生串扰，则

g1(-Tb)]+cΔω

(20)

因此可以得到实际反馈电平值为

(21)

这样，接收机在实现每一帧AIS信号的位同步和帧同步时，便可以同时计算出用于反馈判决的反馈电平，提高了实时性，降低了系统复杂度.

3 改进反馈判决算法的仿真验证

首先在MATLAB中生成300帧AIS信号，AIS标准规定了GMSK调制中高斯成型滤波器的BT值为 0.4，每帧包含256比特信息.比特率为Rb=9.6 kb/s，采样率为20Rb，载波频率为4Rb，信道设为高斯信道.多普勒频偏设为 0.5Rb.在接收端，GMSK信号先通过正交数字下变频到基带，再通过51阶截止频率为2Rb的矩形窗低通预检测滤波器，来滤除高频成分以及带外噪声，然后通过数字鉴频器解调，解调出的信号通过3 dB带宽为Bo的51阶高斯后检测滤波器，滤除鉴频噪声.

3.1 验证后检测滤波器对误码性能的影响

为了验证后检测滤波器带宽Bo对误码性能的影响，在不考虑反馈判决的情况下，对Bo=0.1Rb～0.8Rb，以及不采用后检测滤波器的情况进行了仿真，仿真结果如图5所示.图中：横坐标为信号噪声功率比(SNR)，范围选择0～10 dB；纵坐标为误比特率(BER).由图可见，Bo太大或者太小都会使误码性能下降.

图5 后检测滤波器带宽对GMSK解调性能的影响Fig.5 Performance of postdetection filter with different bandwidths for GMSK detection

3.2 验证改进的反馈判决算法

根据3.1节的实验，选择后检测滤波器3 dB带宽Bo=0.3Rb，0.4Rb，0.5Rb，来验证改进的反馈判决算法，并与传统的反馈判决算法作对比.在改进的反馈判决算法中，反馈电平采用式(21)的计算方法，传统的反馈判决中，将式(21)中的g1()改成g()来计算反馈电平.实验结果如图6所示.由图可见，当后检测滤波器带宽较大(Bo=0.5Rb)时，改进反馈判决和传统反馈判决方法的性能接近；当带宽较小(Bo=0.3Rb，0.4Rb)时，误码性能进一步提高，而改进的判决反馈方法要优于传统方法.另外，由于鉴频器的非线性作用，噪声产生的干扰，叠加到理想的鉴频波形上.当噪声较小(SNR值较大)时，非线性干扰较小，当前时刻鉴频波形主要受到前后时刻信号的串扰，因此采用反馈判决或本文的改进方法可以降低BER；当噪声较大(SNR值较小)时，噪声引起的非线性干扰将远大于前后时刻信号的串扰，因此无论是否采用反馈判决法，BER都将急剧增高，因此这也是非相干解调固有的门限效应，从仿真的结果也可以验证这一点.因此，本文的改进方法在噪声不是特别大(SNR值不是特别低，如SNR>4 dB)的情况下，效果明显，且优于传统反馈判决算法.

图6 改进的反馈判决和传统反馈判决的性能对比Fig.6 Performance comparison of modified and traditional decision feedback method using postdetection filter with different bandwidths

4 结语

本文通过分析GMSK非相干解调中后检测滤波对有用信号造成的失真，将失真转化为增加的ISI，通过改进的反馈判决算法来补偿，并以高斯后检测滤波器为例，建立了改进后的反馈电平和后检测滤波器的带宽之间的定量关系；同时利用AIS信号中位同步序列和帧起始标志，给出了一种实际系统中实时计算反馈电平的方法.本文提出的方法简单有效，可以应用到卫星AIS接收机以及其他深空通信系统中.另外，对于采用Viterbi检测的GMSK非相干接收机，后检测滤波引起的鉴频输出失真，同样会对寻找最短距离的译码路径造成影响，因此需要通过修正路径距离的计算公式来补偿失真.本文关于失真的分析，对于Viterbi检测也同样具有参考作用.