凸显核心素养价值，培养数学思维能力——以《探索勾股数——像数学家一样思考》为例

浙江省杭州市桐庐县旧县中心学校 叶玉娣

2018年10月17日，富阳区永兴学校初中部开展了主题为“基于数学素养发展的初中拓展课程的构建与实施”的研修活动，我有幸参加了此次活动。活动先安排永兴中学的两位老师各上了一节展示课，其中段春炳老师上的一节《探索勾股数——像数学家一样思考》让我印象很深。段老师从学生已有的认知（刚刚学完的勾股定理）出发，引导学生进行研究性学习，引导学生走向思维的深度，从而提升学生的思维能力。

一、课堂教学实录

（一）引出研究课题

1.让学生观察“普林斯顿322号泥板”，根据所学的历史知识猜猜该泥板来源于哪个文明古国及其大致的年代和出土的地点。

问题刚提出，一位男生踊跃举手发言：“上面记载的文字属古巴比伦语，可推测所属年代在公元前1600年以前。”（这一问一答使我们在场的所有听课老师都唏嘘不已，激发了学生和老师的学习兴趣）

2.泥板上有三列文字，没有人能解释。直至1945年，Neugebauer和Sachs经过细心考究，发现泥板上是三列数字。你知道这些数字与直角三角形的关系吗？借助计算器进行探索。

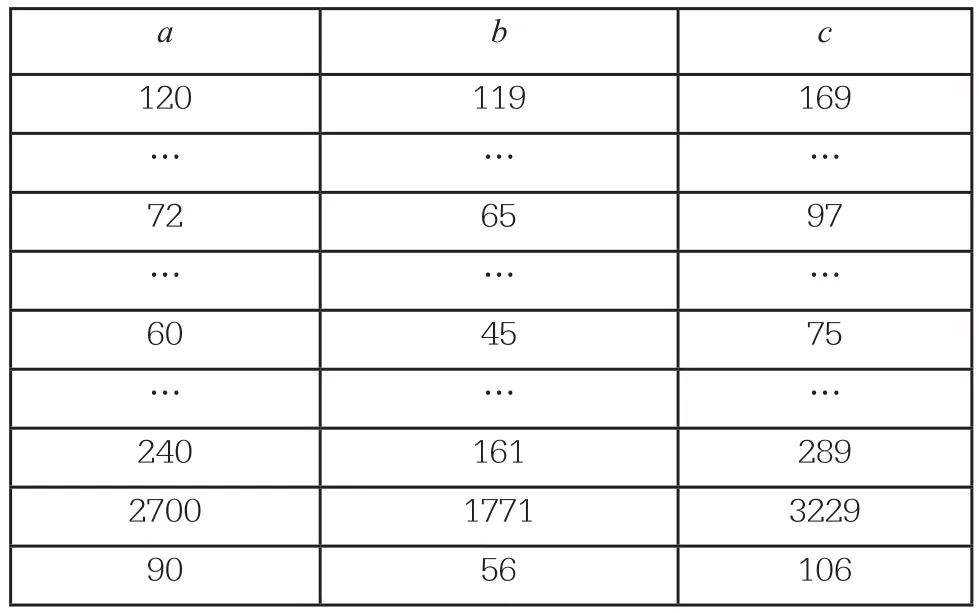
a b c 120 119 169………72 65 97………60 45 75………240 161 289 2700 1771 3229 90 56 106

学生通过动手实践、自主探索、合作交流，学生发现表格中同一行的三个数字恰构成一组勾股数。教师及时给予鼓励，表扬学生个个都是未来的数学家，激发了学生的求知欲和探索精神。

3.教师询问学生：用什么方法判断60，45，75是一组勾股数？

学生1：用平方和计算，验证602+452是否等于752。

学生2：用平方差公式计算：752-452=（75+45）（75-45）=120×30=3600=602。

学生3：45，60，75是勾股数3，4，5的15倍。

通过比较，学生能感受到后两种计算方法更加简单快捷，激励自己应当提高运算能力，理解运算的算理，发展思维能力（为后面的规律推理埋下伏笔）。

（二）观察与探究

1.组织学生说出知道的勾股数。（先小组合作，再班级交流）

学生列举的勾股数（学生列举是无序的，为了便于发现规律，老师的书写是有规律的，如下表）

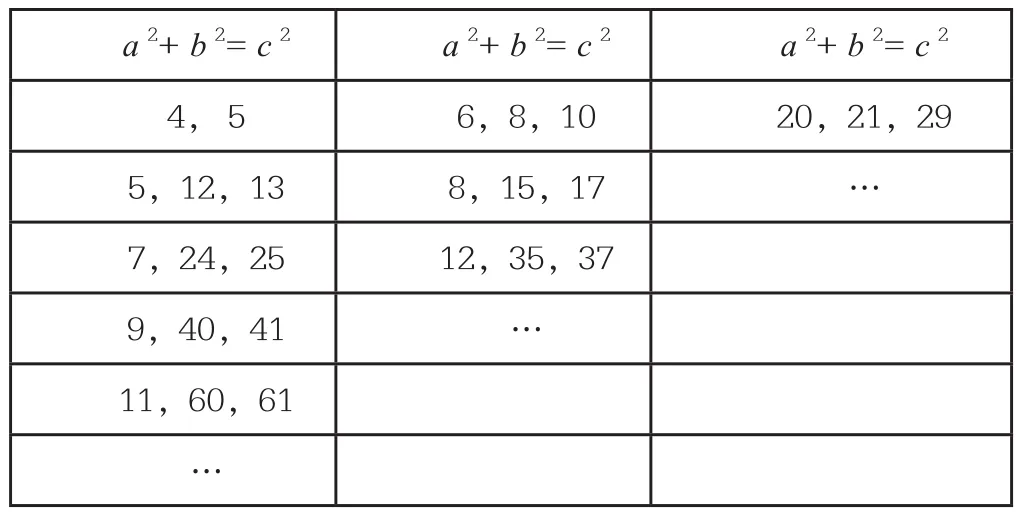
a 2+ b 2= c 2 a 2+ b 2= c 2 a 2+ b 2= c 2 4， 5 6，8，10 20，21，29 5，12，13 8，15，17 …7，24，25 12，35，37 9，40，41 …11，60，61…

2.观察这些勾股数，你有什么发现（规律）？

学生提出了一些想法：（1）第一列：当a是奇数时，c-b=1;（2）第二列：当a是偶数时，c-b=2;（3）a、b、c不能都是奇数……

3.根据你的发现，是否能写出更多的勾股数？学生推理：（1）当a是奇数时，c-b=1 ①，

∵ c2-b2=a2，即（c+b）(c-b)= a2，

∴c+b=a2②，

师生共同归纳两种求勾股数的公式：

4.你是否可以提出其他新的问题？

学生1：勾股数3，4，5是我们最常用的勾股数，也很特别，因为是连续的三个正整数，这样的勾股数是否是唯一的？

学生2推理：假设m-1，m，m+1是三个连续的正整数，且是一组勾股数，那么（m-1）2+m2=（m+1）2，整理得：m2-4m=0，解得m1=0（舍去），m2=4，所以三个连续正整数的勾股数只有3，4，5这唯一一组。

5.是否能够得到所有勾股数的公式（或方法）？

勾股数又称商高数，它有无数组，是有一定规律的。比如有一组求勾股数的式子：a=m2-n2，b=2mn，c=m2+n2（其中m，n为正整数，且m＞n）。你能验证它吗？

解：∵ a=m2-n2，b=2mn，c=m2+n2，

∴a2+b2=(m2-n2)2+(2mn)2=(m2+n2)2，

∴a2+b2=c2。

故a，b，c为勾股数。

利用这组式子，完成下表：

其实，任意一组勾股数（a，b，c）可以表示为如下形式：a=k（m2-n2），b=2kmn，c=k（m2+n2），其中，k，m，n均为正整数，且m＞n。

（三）学习数学家的智慧

提供相关史料，组织引导学生阅读理解数学家的思考方法：

1.几何代数法：毕达哥拉斯、柏拉图、欧几里得、刘徽基于不同文化背景的巧妙设计。

2.丢番图巧妙的代数图形方案已脱离几何，走向代数学。

介绍古希腊数学家毕达哥拉斯（约公元前580年～500年）的证明方法：

如图：∵1+3+5+7+……+（2n-1）=n2，

∴ 1+3+5+7+……+（2n-1）+（2n+1）=（n+1）2，

∴ n2+（2n+1）=（n+1）2。

令2n+1=m2，

则 n2+m2=（n+1）2，

整理得：n2+m2=n2+2n+1，

让学生感受数学家的智慧，学习像数学家一样思考，增加学习数学的兴趣，培养正确的思维方式，提升思维能力。

（四）概括整理 感悟提升

我们要努力学习，接过数学家手中的接力棒，让数学之路越走越远！

二、感悟

经过这次研修活动，深感自己肩上的责任重大，深感自己专业素养不足。相比较，我的数学课堂教学只是为了让学生应付升学考试，没有把数学本身的学科意义渗透到学生的思维品质里。对教材里的拓展性课程视而不见，教师越教越死，学生越学越死，对数学学习失去兴趣、失去信心。所以，作为数学老师，我们要转变观念，除了教知识，更要去思考如何培养学生的数学素养，特别是如何在课堂教学中体现与落实数学核心素养，培养思维能力。

首都师范大学数学科学学院教授，博士生导师王尚志教授曾经举过一个发人深省的例子：一所“985”高校，学生的高考数学平均分在125分以上，入学后的10月份组织学生做做过的高考题目的考试，平均分降到100分；到同一年的12月再考一次同样的题目，平均分只有及格。这个例子说明很多题目学生做过就忘了，考那样的题目，没有多大的积极意义，学生的能力并没有得到真实的提高。这也告诉我们生活中绝大多数人毕业后如果不从事数学专业工作，便不再记得那些数学公式、定理、解题方法，所以我们数学老师应该思考的问题是关注学生能否用数学的思维方法去解决生活中的实际问题，这才是社会发展真正需要的数学教育。

（一）什么是核心素养

林崇德教授及其团队曾做了这样的描述：核心素养是学生在接受相应学段的教育过程中，逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力。

（二）什么是数学核心素养

数学核心素养是具有数学基本特征的适应个人终身发展和社会发展需要的人的关键能力与思维品质。不严格地说，数学核心素养不仅包含外显能力，还包含内在思维品质。例如在数学方面，可以解决一个问题或解答一个题目，但对解决问题思想的理解深度是有差别的。前者体现出能力，记忆或模仿也可以帮助解决问题，后者反映出思维品质，内在地、持续地发挥作用。

（三）如何在数学课堂教学中落实核心素养

既然核心素养是一种能力、一种思维品质，那么核心素养的养成就不能依赖单纯的记忆和模仿，而应当依赖感悟和思考，所以核心素养的培养就是思维能力的培养。我们老师应该在核心素养的视角下，以数学知识为载体，以数学概念的内在逻辑为线索，精心选择学习素材，构建学习情境，设计符合学生认知规律的、自然而目标明确的系列数学活动。引导学生通过多样化的学习方式，让学生在掌握所学知识技能的同时，也能感悟知识的来龙去脉，形成思维能力。这一点段老师给我们起了一个很好的示范和引领，下面是我通过听课后的一些粗浅想法，不知道有没有领悟到段老师的真谛。

1.激发学生的思维活动

课标中指出：义务教育阶段数学课程的设计，应充分考虑本阶段学生数学学习的特点，符合学生的认知规律和心理特征，应设计有利于激发学生的好奇心和求知欲的数学活动。

在环节（一）中，段老师要求学生对“普林斯顿322号泥板”做一个经验性的判断。这一设计不仅激发了学生的学习兴趣和求知欲望，也给我们所有听课的老师普及了课外知识。另一方面也让学生了解到数学知识都是经过历史积淀，通过问题、猜想、论证、检验、完善等过程一步一步成熟起来的。

2.点燃学生的思维火花

课标中指出：义务教育阶段数学课程的设计应重视学生已有的经验，设计符合学生认知规律，有利于引发学生思考的数学问题。学生的学习应当是一个生动的、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式。学生应当有足够多的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。在呈现作为知识和技能的数学结果的同时，应使学生体验构建数学模型、寻求结果、解决问题的思维过程。

在环节（二）中，段老师设置了5个问题，从学生刚刚学完的勾股定理出发，让学生经历了观察（熟悉的勾股数）、发现或猜想（关于勾股数的一些规律）、验证或证明的过程。在这些过程中，学生的思维被层层打开，引导学生进行研究性学习和引导学生走向深度学习。老师要多问几个为什么，提高学生发现问题、提出问题、分析问题、解决问题的能力，培养学生思维能力的深刻性。

3.提升学生的思维深度

课标明确提出要使学生初步了解数学产生与发展的过程，体会数学对人类文明发展的作用。介绍必要的数学史知识可以使学生在平时的学习中对所学问题的背景产生更加深入的理解。古代数学家的思维方式可以作为一种学习资源，能激发学生的学习兴趣。在解决问题的过程中感受数学家的艰辛，学习数学家坚持不懈的品质。

在环节（三）中，段老师组织引导学生阅读理解数学家毕达哥拉斯的思考方法，培养学生几何直观的能力，感受数学家的智慧，学习像数学家一样思考，培养吃苦耐劳的精神，培养正确的数学思维方式，提升学生思维的广度和深度。

整堂课在段老师的引领下“谈古论今”，在解决一个又一个数学问题的同时，让我们感受到老师较高的专业素养。段老师鼓励学生要努力学习，从容地接过数学家手中的接力棒，无一不在培养学生的思维品质。所以如何在核心素养的视角下培养学生的思维能力，关键在于提高教师的专业素养。试想我们的数学课堂每次都在自己预设的框架中进行，学生的思维被桎梏得死死地，怎能提升学生的思维能力？试想一位老师都害怕学生在课堂上提出一些自己都没有想到的问题，而不能从容面对，那学生又如何能信服于你？试想一位老师连最基本的数学史都不了解，不清楚知识的来龙去脉，那又如何来更好地引导学生的学习，开发学生的思维广度呢？所以人们常说：“给学生一杯水，教师要有一桶水、一缸水甚至一江水。”比喻教师要教好学生，自己必须有比学生更丰富的知识，所以我们教师平时要不断地学习，掌握真才实学，才能不“误人子弟”。

听了这节课，我觉得教师有良好的数学核心素养是进行核心素养下的数学课堂教学的先决条件，教师要从学生成长的高度去思考教学，注重学生思维能力的培养，帮助学生学会“用数学的眼光看世界”“从数学的角度看问题”“用数学的方法去解决”。