中国证券公司系统性风险测度及演化特征研究——来自20家上市证券公司的数据

刘 超，李元睿，姜 超，马玉洁，刘宸琦，谢启伟

(1.北京工业大学经济与管理学院，北京 100124；2.北京现代制造业发展基地，北京 100124；3.南加州大学，洛杉矶 90089)

1 引言

2008年美国次贷危机和2010年欧洲债务危机爆发后，系统性风险的度量及风险演化规律成为世界各国关注的热点问题。证券业是金融业中的高危行业，行业内部的风险具有较强的传导效应。我国证券市场的资产规模仅次于银行业，对整个金融系统的风险溢出效应较大[1]，而证券公司是资本市场的主体机构，一旦发生重大风险，必然会引起融资不畅、资本市场信心受挫、客户蒙受损失等一系列连锁反应，甚至通过关联业务渠道对整个金融业乃至实体经济的发展造成影响。在我国证券公司近二十年的发展中，随着开放程度日益提高，业务范围不断扩大，金融衍生产品种类越来越多，其面临的风险将越来越高。尤其在近几年的综合治理之后，证券公司已逐渐发展成为我国金融体系中的重要组成部分。同时，经济全球化和国际金融一体化的发展在提高资本配置效率的同时，也使得各国金融系统抵御风险的脆弱性进一步加强，证券公司面临的风险进一步加大[2]。因此有必要对我国证券公司的系统性风险进行深入研究，寻找监测风险的科学方法，揭示系统性风险的演化特征，进而寻求防范风险的有效途径。

2008年的金融危机之前，对风险的监管多停留在个体层面的微观审慎监管模式。危机爆发之后，国际监管当局普遍认识到微观审慎监管容易忽视掉经济系统中的一些致命风险，而宏观审慎监管能够有效弥补监管盲点[3]。尤其是巴塞尔协议Ⅲ实施之后，微观审慎与宏观审慎监管相结合的理念越发引起监管当局的重视。这促使学术界和监管部门加大了对系统性风险的重视，对系统性风险的研究在理论层面和实证层面都取得了长足的进展，但这些研究多集中于银行体系，对证券公司系统性风险的研究并不充分，且大多数研究仅停留在微观或宏观的某一层面，没有将二者结合起来综合考量。

动态测度系统性风险是刻画系统性风险演化特征的前提和关键。在险价值(Value at Risk, VaR)模型[4]及其延伸出的CoVaR[5]，SES[6]，MES[7]以及SRISK[8]等方法是测度单个机构风险的主流方法。这些方法在实际应用中都展现出一定的优势，但不足之处在于运用的数据较为单一，对风险的全面性把握不足。而Gray等[9-10]基于“Black-Scholes模型[11-12]”提出的未定权益分析(Contingent Claims Analysis, CCA)结合机构的资产负债表数据和市场数据等多方面信息刻画风险，具有良好的前瞻性和准确性[13]。CCA模型被广泛应用于系统性风险研究，如Castren和Kavonius[14]，Antunes和Silva[15]，宫晓琳[16]，吴恒煜等[17]等。

CCA模型能够很好地在微观层面测度单个机构的风险，但在应用于宏观层面对系统性风险进行测度时，通常是将整个体系模型看作一个公司来处理，没有考虑机构之间的风险相依性。因此，Gray和Jobst[18]对CCA模型进行拓展，结合极值理论和Copula函数形成了可以测度了多家金融机构联合违约风险的新方法，被称为系统性未定权益分析(Systemic Contingent Claims Analysis, SCCA)。SCCA作为一套科学、完整的风险测度方法受到监管当局的重视，国际货币基金组织IMF[19]多次使用SCCA方法对各国进行实证应用，先后对美国，英国，瑞典，德国，西班牙等国家进行了压力测试和金融稳定评估。巴曙松等[20]首次将SCCA方法引入国内研究，介绍了SCCA方法的基本模型及相关金融风险指标的度量。此后，国内学者对SCCA技术的应用展开了广泛研究，如李志辉等[21]，王擎等[22]，叶五一等[23]，陆静和张佳[24]。

从现有研究来看，对于SCCA技术及相关指标的研究和应用仍处于起步阶段，对SCCA理论框架的延伸仍有待继续完善。关于SCCA及相关方法的应用多集中在银行体系或国民经济部门层面，对于证券公司的相关研究不足。近年来，随着金融风险跨市场跨行业的传染性日益增强，来自证券公司的系统性风险将对金融市场乃至整个实体经济造成巨大影响，因此有必要对证券公司的系统性风险进行有效的度量。针对SCCA技术理论框架庞大，在操作和实现上比较复杂、困难的特点，本文对SCCA技术进行了改进，提出了测度系统性风险的新指标，并将其应用于我国上市证券公司系统性风险进行的实证研究中，从微观和宏观两个层面动态测度了我国上市证券公司个体风险及系统性风险，并结合风险指标分析了系统性风险的演化规律和特征。为系统性风险的测度和识别提供了方法支持，为监管当局提出了相应的政策建议。

2 研究方法及模型构建

2.1 研究设计

SCCA技术是对CCA模型的拓展。该方法采取动态的滚动窗口法，首先运用CCA模型测度单个证券公司在窗口期的预期损失值以刻画其面临的风险状况；其次借助极值理论的思想对该窗口期内的证券公司损失分布建模，着重描述监管当局关心的尾部分布；然后将各证券公司的边际分布通过Copula函数进行连接，构造整个证券公司系统的预期损失联合概率分布；最后模拟计算每个窗口期整个证券公司系统的风险指标J-VaR*，动态地刻画系统性风险的演化过程。在这个思路下，将SCCA技术的整体研究设计表述如图1。

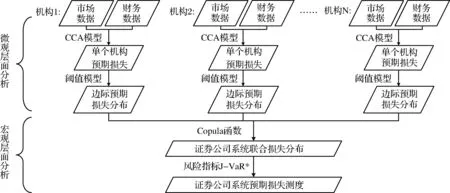
图1 SCCA技术研究设计

2.2 单个证券公司预期损失

高负债经营是证券行业的一个基本特点，这种经营模式可以利用杠杆效应来扩大收益，但同时也带来了潜在的预期损失。Merton[12]最早将期权定价理论应用于公司层面的违约风险测度，能够具有前瞻性地得出违约距离、违约概率以及预期损失等风险指标。本文主要通过对单个证券公司的损失程度衡量整个系统的风险状况，故采用预期损失指标度量单个公司的个体风险。

定义证券公司t时刻的资产市场价值At在时域上随机波动，且等于t时刻股权的市场价值Et与风险债务的市场价值Dt之和：

At=Et+Dt

(1)

其中Dt具有高级别的索取权，而Et具有低级别的索取权。设t时刻，该公司承诺在T时刻偿付的债务账面值为Bt，则t时刻市场隐含预期损失Lt可表示为：

Lt=Bte-r(T-t)-Dt

(2)

Lt反映了单个证券公司面临的风险大小，为测度风险，需对资产价值At的运动进行考量。CCA模型假设公司的资产价值At服从漂移常数为μA, 波动率为σA的几何布朗运动：

dAt=μAAtdt+σAAtdZt

(3)

其中Zt表示标准布朗运动。漂移常数μA代表资产的预期收益率，但由于μA的值难以准确获得，在实际操作中常使用无风险利率r代替μA。从上式可以看出At随时间不断波动变化，有可能在某一偿债期T时刻跌破承诺偿付的债务账面值Bt，从而发生债务违约。这与期权定价模型十分类似，因而根据Merton[12]的研究，可将证券公司的股权市场价值Et看作基于资产价值的欧式看涨期权，将证券公司的账面债务值Bt看作期权的敲定价格，由“Black-Scholes”期权定价公式可得：

Et=AtN(d1)-Bte-r(T-t)N(d2)

(4)

其中：

(5)

(6)

N(x)为正态分布累积分布函数。而证券公司的市场隐含预期损失可以看作欧式看跌期权：

Lt=Bte-r(T-t)N(-d2)-AtN(-d1)

(7)

一般而言，证券公司的隐含资产波动率σA难以直接观测，但可以根据其与股权市值波动率σE之间的关系来计算：

EtσE=AtσAN(d1)

(8)

将(5)，(6)式带入(4)式，并联立(4)，(8)两式，除At和σA两个未知数以外，其他参数都可以通过市场及财务数据获得。求解该非线性方程组，得到At和σA的值，并代入(7)式，可求得t时刻该证券公司的预期损失值Lt。

综上，利用CCA模型求解单个证券公司的预期损失分布的流程可由图2表示。

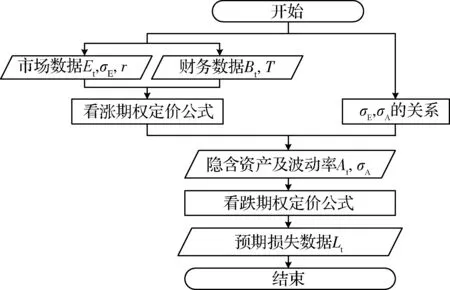
图2 单个证券公司预期损失计算流程

2.3 单个证券公司的边际损失分布

设X1,X2,…,XS为单个证券公司在某窗口期的S个损失样本，令MS=max{X1,X2,…,XS}，若X1,X2,…,XS独立同分布且已知Xi,i=1,2,...,S的分布，则极值MS的分布可以表示为[25]：

Pr(MS≤x)=Pr(X1≤x,X2≤x,…,XS≤x)=Pr(X1≤x)Pr(X2≤x)…Pr(XS≤x)=FS(x)

(9)

但在实际中，Xi的分布往往不能准确获得，因此也难以精确计算MS的分布。然而，当S→∞时，经过适当的规范化，可以得到MS的渐进分布H(x)。由Fisher-Tippet定理可知：若存在常数列{aS>0}和{bS}，使得：

(10)

则H(x)是Gumbel分布，Fréchet分布或Weibull分布这三类极值分布中的一种。

极值理论提供了寻找极端值的分布的理论依据。在此基础上，对金融风险的测度进行建模时通常有两种选择：一类是区间极大值模型(Block Maxima Model)。但是由于风险在积聚和爆发时，极端统计观测值往往较为集中，采用区间极大值模型将会忽略掉一些具有丰富信息的数据[26]。另一类方法是阈值模型(Peaks Over Threshold)。这类模型利用超过某一临界值的所有极值数据来刻画损失分布的尾部轮廓。由于阈值模型相对于区间极大值模型保证了极端数据的完整性，更精确地刻画证券公司预期损失分布的尾部特征，故本文采取阈值模型对单个证券公司的预期损失数据进行处理。

阈值模型的建模思想是通过对超出阈值的尾部数据渐进拟合为某一极值分布，并找到尾部分布与整体分布之间的关系，从而估计出整体分布。设损失样本X服从分布F(x)，定义u为阈值，超过阈值的超出量Y=X-u的分布可表示为：

(11)

整理可得尾部分布与整体分布之间的关系式：

F(x)=Fu(y)(1-F(u))+F(u),x≥u

(12)

在对尾部分布的刻画中，根据DuMouchel[27]的研究，设定足够大的阈值u，则超过阈值的超出量Y渐进服从广义帕累托分布：

(13)

当ξ≥0时y≥0，ξ<0时0≤y≤-σ/ξ。其中，ξ表示形状参数，σ表示尺度参数。当ξ为正时，G(y;ξ,σ)为厚尾分布，且随着ξ的增大厚尾特征越发显著。分布中的参数ξ和σ可通过极大似然估计法得出。u值的选取是阈值模型的关键，u值太大，则将只有较少的超出量，造成样本不足；u值太小，则超出量分布不能准确地被广义帕累托分布拟合，估计量将成为有偏估计[28]。u值的选取通常使用样本平均超额函数方法，但此方法的主观性较大，且难以对大量的窗口期数据进行批量处理，故本文采用峰度法[29]找到正态分布与偏态分布的交点，以此确定阈值u，具体做法为：

算法1 基于峰度法确定阈值uStep 1:计算窗口期内单个证券公司损失样本数据的均值X与峰度KS;Step 2:判断峰度值,若KS≥3,则选取使得|Xi-X|值最大的Xi,将其从样本从剔除;Step 3:重复Step 1,Step 2,直到样本的峰度小于3;Step 4:在剩余的样本中,选取最大的样本值作为阈值u的取值。

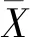
(14)

(15)

在实际操作中，预期损失样本中大量的小额数值容易使阈值估计失真。根据李志辉等[21]的研究，过小的预期损失样本数据对整个系统的影响有限，有必要对损失的规模进行界定，将小额的预期损失剔除以保证阈值的准确性。具体做法为：首先设定预期损失规模的下界，将低于下界的数据剔除；然后对剩余的数据利用峰度法求出阈值u的初步估计值；再进行Kolmogorov-Smirnov检验，如果不拒绝原假设，则认为阈值的取值是合理的，如果拒绝原假设，则适当提高损失规模的下界，继续重复上述步骤，直到得出合理的阈值。

阈值u的选取确定后，即可得到阈值超出量Y的渐进分布G(y;ξ,σ)，用G(y;ξ,σ)替换(12)式中的Fu(y)，可以得到单个证券公司的边际预期损失分布：

(16)

其中，预期损失小于阈值的概率F(u)可由历史模拟法获得，即：F(u)≈(S-Su)/S，S表示该窗口期样本总数量，Su表示超出阈值的样本数量。

综上，利用阈值模型求单个证券公司的边际预期损失分布的具体流程如图3所示。

图3 单个证券公司边际预期损失分布计算流程

2.4 证券公司系统的联合损失分布

在得出窗口期内单个证券公司的预期损失分布后，可以进一步对单个公司的个体风险进行刻画。在考量单个证券公司风险的基础上，还应该试图探索公司之间的风险联动性，继而刻画整个系统的风险变化情形。Sklar[30]提出的Copula理论指出：可以将一个N元联合分布分解为N个边缘分布和一个Copula函数，该Copula函数描述了变量间的相关性。

多元分布的Sklar定理：令G(x1,x2,…,xN)为具有边缘分布F1(x1)，F2(x2)，…，FN(xN)的联合分布函数，那么一定存在一个Copula函数C(p1,p2,…,pN)，满足：

G(x1,x2,…,xN)=C(F1(x1),F2(x2),…,FN(xN))

(17)

若F1(x1)，F2(x2)，…，FN(xN)连续，则C(p1,p2,…,pN)唯一确定。

由于证券公司的风险之间的相关关系通常是非线性的，并且受外部环境的影响不断地发生着变化。因此考虑采用变量之间相关关系变化的动态Copula来联合各公司之间的预期损失分布，本文采取时变Gumbel Copula函数对各证券公司之间的风险相依性进行刻画。Gumbel Copula函数是Archimedean Copula函数族的一种，它对变量之间的上尾变化十分敏感，能快速捕捉到变量之间的上尾相关变化。Gumbel Copula函数的表示形式为：

C(p1,p2,…,pN)

(18)

其中的参数θ可由两阶段极大似然估计法得出[31-33]。在估计出参数后，结合各证券公司的损失分布函数，可求得各窗口期内整个证券公司系统联合预期损失分布函数G(x1,x2,…,xN)的具体形式。

2.5 系统性风险测度指标

利用分布函数可以构建多种指标来刻画风险，其中VaR采用一定置信水平的分位数来描述风险，是已知损失分布函数来衡量风险的主流方法。但VaR通常适用于单个公司对应的一元概率分布。对于整个证券公司系统对应的多元联合分布不存在一元分布的“分位数”概念，因为在给定的置信水平1-α下，可能有多种不同预期损失组合(x1,x2,…,xN)满足Gt(x1,x2,…,xN)=1-α。因此在将VaR应用于描述多元联合分布对应的系统性风险时，需要对其进行改进。对此，李志辉等[21]提出了J-VaR指标，其定义式如下：

(19)

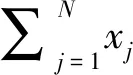
(20)

在对风险指标J-VaR*进行模拟时，需要利用Copula函数的性质。多元Copula函数表示多个变量之间的相关关系，根据N元Copula函数的性质，有:

C(1,…,1,p1,p2,…,pk,1,…,1)

=C(p1,p2,…,pk),k=1,2,…,N

(21)

特别地，当k=1时，有：

C(1,…1,p1,1,…1)=p1

(22)

即在其余变量都取1时，多元Copula函数将变为一个低维度的Copula函数，表示剩余变量之间的相关关系。又对于Archimedean Copula函数，容易证明：

(23)

即一个N元Archimedean Copula函数都可以分解为N-1个二元Archimedean Copula函数。根据这两个性质，本文考虑首先模拟两个证券公司之间的相关关系，再将其视为一个整体与第三个证券公司进行模拟，最终求得整个证券公司系统在一定置信水平下的J-VaR*值。具体算法如下：

算法2 蒙特卡洛模拟J-VaR∗Step 1:生成N-1个在(0,1)上服从均匀分布的随机变量(q1,q2,…,qN-1),并选定置信度α;Step 2:模拟在一定风险相依性下各证券公司的风险状况(p1,p2,…,pN);Step 3:根据特定窗口期内单个证券公司的预期损失分布函数,求得单个证券公司的预期损失xj=F-1j(pj);Step 4:求得一定风险相依性下各公司损失之和∑Nj=1xj的模拟值;Step 5:重复Step 1-4 10000次求平均值,得到该窗口期内的J-VaR∗值;Step 6:将时间窗口向后推移,重复Step 1-5 依次求得研究区间内各窗口期的J-VaR∗值。

在Step 2中，根据随机变量模拟在一定置信水平下，各证券公司的风险状况及风险相依性：

(24)

上式中，结合(21),(22)和(23)式，每一个等式都可以转化为一个一元方程：

(25)

从而可以解得1-α置信水平下的(p1,p2,…,pN)的模拟值。

根据3.3节中利用阈值模型构建的单个证券公司的预期损失分布函数，可求得单个证券公司的预期损失，从而进一步求得各公司损失之和的模拟值。在每个窗口期内进行10000次模拟，并求模拟样本的平均值来逼近其期望值，即J-VaR*，从而在研究区间内动态地描述整个证券公司系统的系统性风险变化。

3 实证结果分析

3.1 数据的选取与处理

在2015年，中国股票市场经历了剧烈动荡，对证券公司的经营造成了巨大冲击。为保证捕捉到风险演化的规律和特征，并使实证结果具有借鉴意义，故本文将数据选取的区间选定为2011年第四季度至2016年第三季度，滚动窗口设为3年，则研究区间为2014年第四季度至2016年第三季度。在中国证券监督管理委员会2016年第四季度公布的上市公司行业分类结果中，“资本市场服务”类共有29家。由于部分公司上市时间较晚，存在大量数据缺失，故选取其中20家的数据作为样本。它们分别是：东北证券、东吴证券、方正证券、光大证券、广发证券、国海证券、国金证券、国投安信、国元证券、海通证券、华泰证券、锦龙股份、山西证券、太平洋、西部证券、西南证券、兴业证券、长江证券、招商证券和中信证券。本文所采取的样本数据的处理方式和来源如表1所示。所有算法均由Matlab软件实现。

表1 样本数据说明表

3.2 单个证券公司预期损失测度

SCCA技术是基于CCA模型的组合方法，通过微观，宏观两个层面刻画证券公司的风险状况。在微观层面，首先运用CCA模型测度单个证券公司的预期损失，捕捉风险在整个数据样本范围内的变动；在宏观层面，利用滚动时间窗口期内的预期损失数据拟合单个证券公司的预期损失分布，并使用Copula函数得到整个证券公司系统的联合损失分布，从而进一步测度在证券公司风险联动下的系统性风险。

首先，在微观层面，由CCA模型测得的单个证券公司的风险指标Lt在整个数据选取区间随时间变化的趋势如图4所示。

图4 单个证券公司预期损失(单位：元)

从图4可以看出：

①由CCA模型监测到的单个证券公司风险主要集中爆发在2015年6月，与2015年我国股市的大规模震荡，证券公司普遍暴露出危机的事实相符合。在2014年底能监测到大部分证券公司风险小幅度积累，但在2015年初有所下降，如东北证券、东吴证券、方正证券、光大证券、广发证券、国海证券、国元证券、海通证券、华泰证券、山西证券、西部证券、西南证券、长江证券、招商证券和中信证券。在所有的20家上市证券公司中，除国投安信、太平洋和兴业证券外，其余公司均在2015年6月份开始有大幅度的风险攀升，并持续贯穿整个2015年，在进入2016年后逐渐缓释。而国投安信、太平洋和兴业证券风险的明显攀升发生在2016年初，滞后于其他公司。

②在风险规模方面，单个证券公司的预期损失在风险爆发时期主要集中在十亿元到百亿元水平之间。本文将2015年风险爆发时期各证券公司的预期损失水平和2015年各公司资产规模整理如表2所示。可以看到，风险爆发时期预期损失在十亿元水平的证券公司，如东北证券、东吴证券、方正证券、国海证券、国金证券、国元证券、锦龙股份、山西证券、太平洋、西部证券、西南证券、长江证券和招商证券，资产规模普遍偏低，集中在百亿元水平，而风险爆发时期预期损失较高，在百亿元水平的证券公司，如光大证券、广发证券、国投安信、海通证券、华泰证券、兴业证券和中信证券等，资产规模普遍偏高，集中在千亿元水平。高负债经营是金融机构的特点，现有研究指出资产规模大的金融机构具有较高的风险贡献[34]，与本文测度的单个证券公司风险结果相符合。

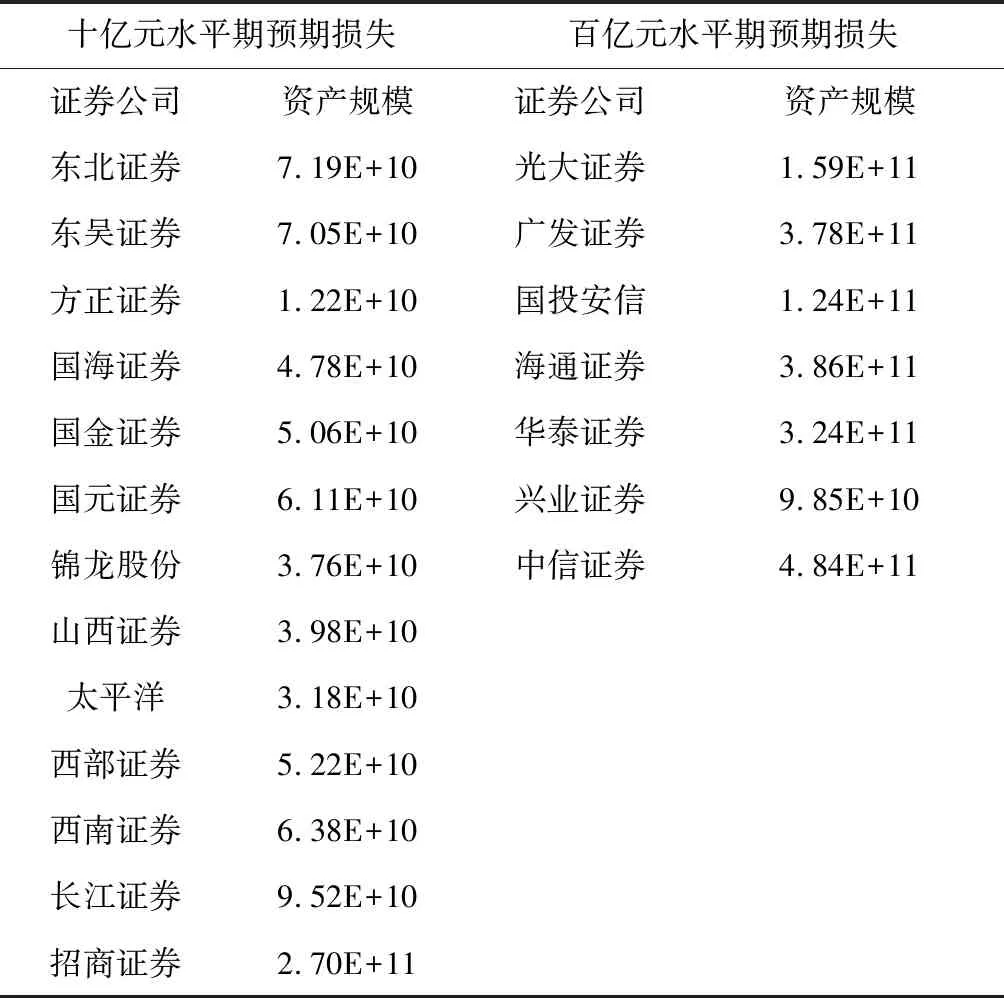
表2 单个证券公司风险水平与资产规模对比(单位：元)

注：资产规模数据来源于中国证券业协会

3.3 单个证券公司风险演化特征分析

在得到样本区间内单个证券公司的风险值后，将单个证券公司各时间窗口内的数据拟合为广义帕累托分布，以刻画该窗口期内的预期损失分布。广义帕累托分布的形状参数ξ>0时，具有厚尾特征，且随着ξ的增大厚尾特征越来越显著。因此，形状参数ξ能够较好地反映单个证券公司的风险演化趋势。由于滚动窗口期设为3年，对应的研究区间为2014年三季度至2016年三季度。将研究区间内的各证券公司预期分布的形状参数ξ的变化表示如图5所示。

从图5可以看出，在形状参数的大小方面，由各证券公司窗口期内数据测得的形状参数在(0,4)之间波动，表现出一定的厚尾性。形状参数随时间的变化也反应了不同时期各证券公司面临的风险状况。结合图4，我们可以得出：

①系统性风险在大规模爆发前往往会有部分公司共同表现出的小型波动前兆，提前期约为6个月。在图4中，2015年6月风险大规模爆发之前，大部分证券公司在2014年12月均表现出小幅度的风险波动。在风险集体攀升的2015年，各证券公司的形状参数ξ普遍较大，在2016年风险缓释阶段，形状参数普遍较小。在参数的波动方面，我们可以看到在2014年四季度之后ξ值持续走高的情形下，大多数证券公司在2015年初都有明显的回落，与之后的继续攀升形成了断层，这与图4中风险大规模爆发前，有部分小规模风险积聚的前兆相吻合。

②证券公司系统性风险的积累具有一定的隐蔽性，在风险演化过程中具有“陡增缓降”的特点。图4中，在2015年6月份之后的大规模风险爆发时期，各证券公司的风险指标急剧攀升，在随后的一年内持续波动，逐步回归正常水平。图5中，各证券公司形状参数的波动幅度在风险爆发时期不尽相同，但都在风险缓释阶段趋于平稳，这说明危机时期风险的相互传导能力较强，风险的传导和冲击造成了各公司预期损失分布随时间不断变化。而缓释时期由于各证券公司之间的风险传导逐步减弱，表现出一定的独立性。因此，在系统性风险爆发期间，各证券公司的风险并不是一次性的“积聚—爆发—缓释”，而是表现为在多次较大幅度波动中逐渐减小，这说明系统性风险爆发时，造成了体系内的多轮冲击，冲击力度在监管治理和市场调节的作用下逐步放缓，直至风险指标回归正常水平。

3.4 证券公司系统预期损失测度

在宏观层面，SCCA技术基于对单个证券公司测度的风险值，建立证券公司系统联合损失分布，使用蒙特卡洛方法模拟出99%置信水平下的风险指标J-VaR*的变化。为了对比其他风险测度的方法，本文将整个证券公司看作单一整体，使用CCA模型测度样本区间内证券公司系统的预期损失值，并求得各时间窗口期内99%置信水平下的最大损失值，记作T-VaR。同时，本文采取传统VaR方法，利用证券公司系统整体的收益波动，计算整体资产在99%置信水平下的最大损失。三种测度方法采用同样的样本区间和滚动窗口期，测度结果如图6所示。

自2014年底至2015年6月，A股形势持续走好，各类伞形信托和配资平台迅速成长，影子银行不断将资金由实体经济转向股市，股市杠杆不断攀升，系统性风险在该时期逐渐积累[35]。2015年6月12日以来，上证综指从5178.19点经历了断崖式下跌，于8月26日跌至2850.37点，A股经历了大幅震荡[36]，系统性风险大规模爆发。在2015年第四季度之后，风险逐渐缓释。从图6可以看出，J-VaR*，T-VaR以及VaR都捕捉到了2015年6月以来的风险大幅攀升，证明了这些指标对风险爆发的准确识别。其中，J-VaR*与T-VaR走势接近，在整个研究区间内波动较大，捕捉到了风险爆发的突然性。VaR指标在研究区间内的风险攀升和缓释阶段都较为平稳，不易于识别系统性风险大规模爆发及演化特征。在指标值方面，T-VaR和传统VaR在整个风险时期相较于J-VaR*更小，这是由于T-VaR和传统VaR是基于正态假设，不能反映金融风险的厚尾特性，因此在一定置信水平下得到的风险值偏低。在风险积累阶段(2014年9月-2015年5月)，J-VaR*相较于T-VaR和传统VaR攀升幅度明显，反映了J-VaR*对风险积累的敏感性；在风险爆发阶段(2015年6月-2015年9月)，J-VaR*振幅明显，曲线上升陡峭，良好地刻画了风险爆发的突然性和振荡性；在风险缓释阶段(2015年10月-2016年9月)，J-VaR*相较于T-VaR和传统VaR迅速回落。这说明了J-VaR*在风险演化的各个阶段能够敏感捕捉到风险变化，对刻画风险演化特征具有良好特性。

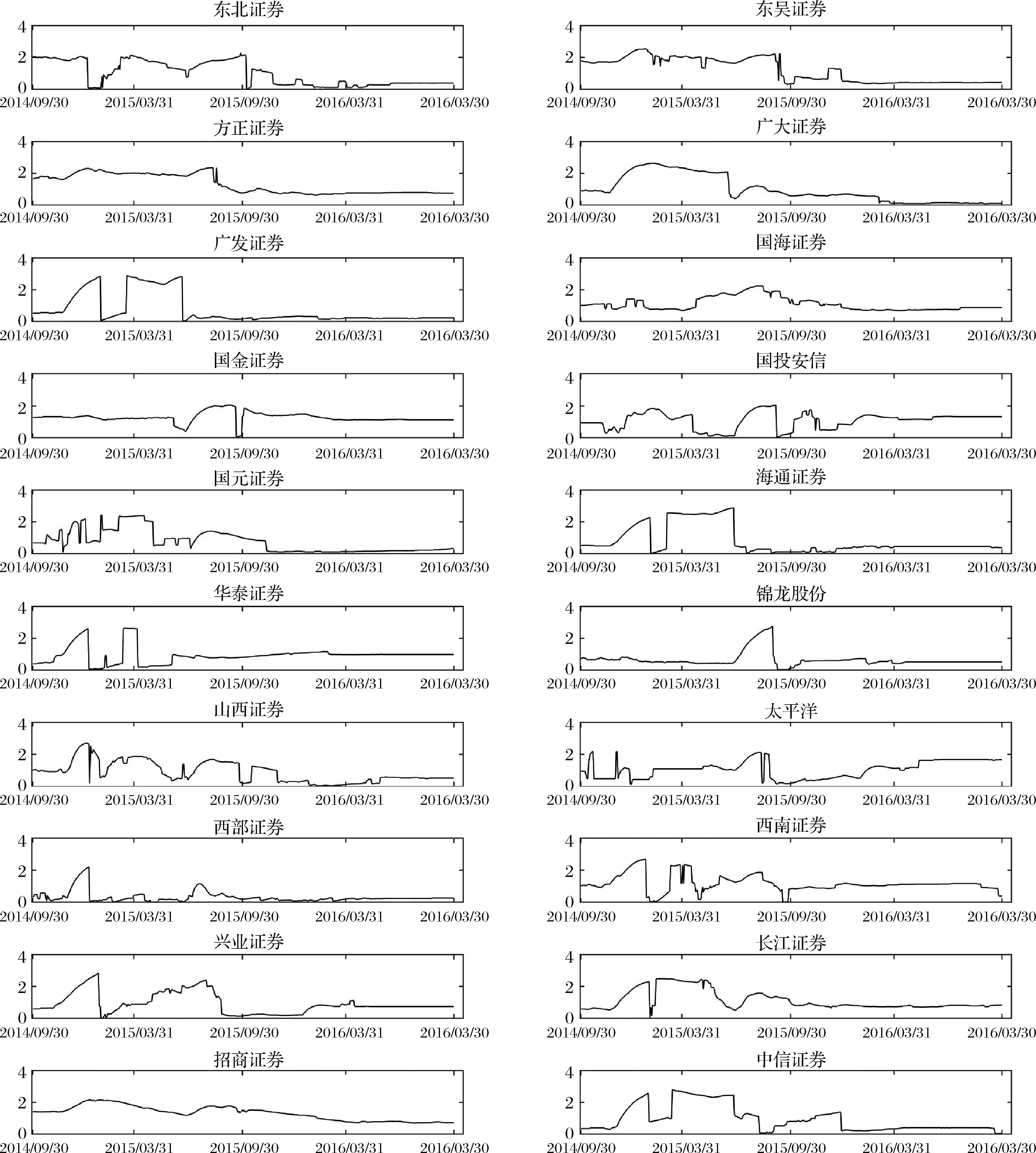
图5 单个证券公司损失分布形状参数变化

图6 证券公司系统性风险指标对比(单位：元)

3.5 证券公司系统风险演化特征分析

从图6中可以看到：J-VaR*的曲线经历了两次大幅攀升的阶段。第一次集中于2015年一季度，曲线上升陡峭，峰值比较集中，与图4中单个证券公司同时期的小幅波动相对应；第二次集中于2015年三季度，整体的风险指标值略低于一季度，但曲线的波动更为剧烈，产生了多个峰值，并与图4中证券公司大面积爆发系统性风险的时期相吻合。结合图4分析可知：

①系统性风险的积累是伴随着微观层面风险相依结构的改变而进行的。在2015年一季度，图4中各证券公司相对低水平的预期损失小幅攀升，在同时冲击的作用下表现为图6中风险指标J-VaR*的陡增，增幅甚至大于2015年6月份以后的大规模风险爆发时期。系统性风险是由各证券公司之间风险相依性和风险事件共同作用而产生的结果，在2015年一季度J-VaR*的陡增是由于各证券公司风险相依结构变得紧密，系统的脆弱性已经突显。所以，在风险积累阶段，监管的重点在于结合宏、微观层面的分析，关注各证券公司之间的风险相依结构的变化，识别潜在的风险。

②系统性风险大规模爆发，是风险在各个证券公司相互传导，形成多轮冲击的结果。图6中J-VaR*的大幅震荡对应于图4中2015年证券公司大规模爆发系统性风险的时期。这个时期中单个公司相对高水平的预期损失并没有完全集中于同一时刻爆发，而是在证券公司之间相互传导，表现为一段时期内的多轮冲击。对于单个证券公司，宏观层面中的短期多轮冲击带来的风险难以及时化解，就会导致风险在微观层面持续累积，拖慢风险释放速度。所以在风险爆发阶段，对系统性风险的防范不仅要关注J-VaR*大小变化带来的冲击，更应关注指标的震荡。在此阶段，监管的重点在于防范截面维度的风险的传染，实施时间维度的逆周期性监管，阻止风险的继续放大和扩散。

4 结语

近年来，随着国际金融危机的频繁发生，宏观审慎监管越来越被监管当局所重视，而对系统性风险的测度是对其进行监管和治理的首要环节。本文基于SCCA技术，并结合国内外学者的研究，对风险指标进行改进，测度了2014年四季度至2016年三季度证券公司系统性风险。将J-VaR*与传统CCA及VaR测度方法进行对比，并以风险事实为基准，表明J-VaR*能够有效捕捉到风险攀升，对风险爆发敏感，对刻画风险演化特征具有良好特性。

在对证券公司系统性风险的实证测度与演化特征分析中，本文得到如下结论：①证券公司系统性风险大规模爆发前，往往伴随着小型系统性风险短期突显的现象，表现为风险相依结构的改变引起的强关联性；②证券公司系统性风险具有“陡增缓降”的特点，其演变过程一般为：首先在风险事件的影响下突然快速攀升，随后风险在一定时间内，在体系内部相互传导，形成对体系的多次冲击，最终逐渐缓释，回归正常水平。

因此，对于风险监管的启示和建议有：①在SCCA技术的应用中，J-VaR*指标短期的突然攀升表现为体系内部风险的集中爆发，反映了风险的强关联性，但在监管中更要注意J-VaR*值的多次大幅波动，其反映了风险在内部相互传导，形成多次冲击的过程；②监管者应识别系统性风险的前兆，做到对系统性风险预防控制,同时也应该把握风险传导过程，良好的风险管理将使风险在多次传导中逐渐稀释，回归正常水平。