基于状态空间模型的宏观经济因素对股市流动性的建模分析

何 迪，周 勇

(1.南京大学经济学院，江苏 南京 210093；2.统计与数据科学前沿理论及应用教育部重点实验室，上海 200062；3.华东师范大学统计交叉科学研究院和统计学院，上海 200062)

1 引言

证券市场的流动性被认为是决定市场行为和市场效率的一个非常重要的因素，是决定一个市场是否有效和稳定的根本性要素。市场流动性稳定，买卖证券的成本小，投资者就会对市场充满信心，证券市场的资源配置效率也就越高。

对于我国股市流动性风险的研究已有很多成果。麦元勋[1]应用Acharya和Pedersen[2]的流动性风险beta对中国股票市场进行了实证研究；刘晓星和邱桂华[3]运用LaVaR 模型检测了我国股票市场所面临的流动性风险最大值；宋逢明和谭慧[4]则通过拉长变现时间将流动性风险引入到VaR中。杜海涛[5]直接估算非流动性指标时间序列的VaR 值；黄峰[6]提出流动性风险是流动性水平偏离其预期水平的变化，并用其变化的方差来衡量。刘洋和刘善存[7]采用上证50 的成分股数据对沪市进行研究，在对市场的流动性风险进行度量后，还分析了流动性风险和收益之间的关系，结果表明，系统流动性风险对中国股市的收益有影响，与国外的研究相似。李延军和王丽颖[8]分别运用Fama-French三因素模型和调整的三因素模型(引入流动性因子和动量因子的五因素模型)，对我国A股市场流动性与股票价格的关系进行实证研究，也得到了类似结果，即样本期内股票流动性对其预期收益的影响非常明显。

如果一国的股票市场完全由供求关系来决定，那么股市和实体经济的发展是一致的。在一个成熟的市场经济国家，如美国或日本，其宏观经济与证券市场的长期关系是基本吻合的。中国还是一个不完全的市场经济国家，证券市场尽管具备了一定的规模，但是在法律、监管、市场引导等多方面的发展还是很不完善，因此，宏观经济与证券市场及其流动性风险之间的关系就必然有其特殊性。

而国内在流动性的研究方面，主要集中在对流动性的阐述和描述上，以及利用定价模型研究流动性与股票收益之间的关系，而有关系统流动性风险的研究，特别是影响因素的研究还较少。张民和朱鲁秀[9]分析了存款准备金率调整对我国股市流动性影响，耿中元和王曦[10]、苏刚[11]实证研究了货币政策对股市流动性的影响，邢治斌和仲伟周[12]利用ARMA(1,2)-GARCH(1,1)模型分别分析了货币政策、财政政策和货币财政政策组合对我国股票市场流动性风险的影响。因此本文旨在研究宏观因素对股票流动性风险的建模、分析与预测。

2 研究方法及模型

2.1 动态因子模型的形式

Stock和Watson最早运用动态因子模型(dynamic factor model) 研究宏观经济变量的共同波动因子，称其为宏观经济景气指数。Koopman等[13]利用状态空间方法建立违约风险的动态因子模型，其中采用了大量的宏观经济变量。本文借鉴其思想，对股市中的流动性风险建立动态因子模型。

我们考虑如下的面板数据的动态因子模型：

(1)

(2)

变量解释：

LIQjt：第j个横截面t时刻的流动性风险指标，j=1,…,J;t=1,…,T。 不同学者提出过很多度量流动性风险的方法，比如买卖价差(bid-ask spread)或相对价差(bid-ask spread/mean bid-ask price) 等直接度量的方法。本文将采用经过Hasbrouck[14]修正后的Amihud[15]非流动性度量指标。j表示公司特征的特定组合，比如行业类别，公司年龄等，本文采用证监会2001 年的上市公司行业分类。

λj：第j个横截面的固定效应。

Ft：t时刻的宏观经济影响用外生因子r×1的向量Ft来描述。流动性风险在横截面之间会相互依赖，通过共同的经济周期、融资条件、货币和财政政策以及一波又一波的乐观或悲观的投资情绪。

2.2 股票流动性指标的选取

对于股票流动性的测度从来都是市场微观结构研究的热点和难点，现有的方法千差万别，人们分别从流动性的各个不同属性的角度对其加以量化，因此至今为止仍没有一个统一的标准。例如，基于高频数据的报价价差及有效价差等直接测度法，即用买卖价格之差来表示受流动性冲击影响所付出的交易成本，适用于较短时间区间。而基于日交易数据的流动性测度指标，如Amihud[15]的非流动性测度(ILLIQ)、 换手率等间接测度指标，则可以用于相对较长的样本进行分析。并且，Goyenko等[18]实证分析结果也表明，Amihud的基于价格冲击的非流动性指标能较好地度量股票的流动性。

Amihud[15]提出使用日收益率的绝对值除以日成交金额这一指标来代表非流动性，它度量了每单位交易对股票价格的冲击。其数值越大，代表同样的成交金额带来的价格波动更大，市场深度越浅，即股票的流动性越差。Hasbrouck[14]对于这一指标提出修正，提出对其求平方根后可以减少偏移，因此实证研究中大多采用经过Hasbrock修正后的Amihud非流动性度量指标

(3)

其中，ILLIQj,t代表股票j在第t个月度的非流动性，Nj,t代表第t个月度内的交易天数，rj.i代表股票j在第t个月度的第i个交易日的对数收益率，Volj,i代表股票j在第t个季度的第i个交易日的成交金额(单位：元)。

因此，我们采用上述指标来作为上证A 股的非流动性的代理变量，在实证研究时，发现取对数形式后拟合程度更高，同时该指标代表非流动性，为了方便查看结果，在计算时乘以-1。 这样，我们得到了流动性指标LIQ，数值越大，代表流动性水平越高。

LIQj,t=-ln(ILLIQj,t)

(4)

2.3 宏观因子的提取和估计

用宏观财政变量对违约风险相互依赖现象的建模是当前一个活跃的研究领域。我们借鉴其方法。用xnt表示大量的宏观经济和金融变量，n=1,…,N。这个面板数据的因子结构可以这样给出

xnt=ΛnFt+ζnt,n=1,…,N

(5)

其中Ft是主成分向量，Λn是载荷的行向量，ζnt是特殊干扰项。将观测到的变量转化为一组个数较少的因子集合这个方法曾被用来预测通货膨胀和生产数据，资产收益率与波动率，以及利率的期限结构。这些研究都表明用宏观因素来预测可以取得良好的结果。

因子Ft可以用主成分方法相合地估计出，即来自宏观经济数据的共同因子Ft可以通过最小化以下的目标函数估计出来

(6)

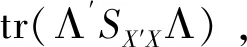
2.4 状态空间模型的形式

状态空间模型对时间序列分析中范围相当广泛的问题提供了统一的解决方法。一般的线性高斯状态空间模型可以表示为如下形式：

yt=Ztαt+t,t～N(0,Ht),

αt+1=Ttαt+Rtηt,ηt～N(0,Qt),t=1,…,n,

(7)

其中yt是p×1的观测向量,αt是m×1的未观测到的状态向量。这个模型背后的思想是：系统随时间的发展是由(7)中第二个式子的αt决定的，但是因为αt不能被直接观察到，我们必须将分析建立在观测值yt上。(7)中的第一个方程叫做量测方程，第二个方程叫做状态方程。误差项t和ηt假设是序列独立的而且各个时点上是互相独立的。矩阵Zt和Tt-1允许依赖y1,…,yt-1。状态向量的初值α1假设服从N(a1,P1)并与1,…,n和η1,…,ηn独立，这里a1和P1先假设是知道的，否则可以使用扩散初始化。在实践中，矩阵Zt,Tt,Rt,Ht和Qt的部分或全部依赖于一个未知的参数向量ψ。

(1)可以被表示成

(8)

状态向量αt包含了未知系数。转移方程提供了随时间变化的状态向量αt的模型，即

(9)

方程(8)-(9)记为Model 1，属于线性高斯状态空间模型，在Durbin和Koopman[19]中有详细讨论。在我们的建模中，大多数未知系数是状态向量αt的一部分，可以通过滤波和平滑的步骤来估计。这个建模方法大大提高了估计步骤的计算效率。剩余的参数收集在一个系数向量ψ=(φ,σ2,β1,…,βJ)′中，可以通过极大似然的方法来估计。

(10)

其中，状态向量为αt=(λ1,…,λJ,γ1,1,…,γr,1,…,γ1,J,…,γr,J)′。 那么状态方程就成为αt+1=αt。 该模型记为Model 2。

(11)

3 实证结果及分析

3.1 数据选取及初步分析

3.1.1 股票数据

本文以上海证券交易所A股市场为研究对象，选用日交易数据进行流动性分析，样本期间是2002年1月4日到2017年12月31日，共192个月度，数据来源为国泰安数据库(http://www.gtarsc.com/)。为尽量减小统计误差，我们又对股票进行了精心地选择：剔除了特别处理(ST)股；由于新股上市后一段时间价格波动较大，考虑到数据的稳定性，我们仅选取2002年1月1日前上市的所有公司。这样处理后，共有525支股票。

根据证监会2001年行业分类将选取的所有个股分成13组(j=1,…,13)。对每一个行业组合j，由日交易数据(开盘价、收盘价、交易金额)计算该行业组合内每一支股票的月度流动性指标，见(4)。再将这些流动性指标简单平均，作为第j个行组合的平均月度流动性LIQj,t。以行业组合C制造业为例，它的平均月度流动性见图(1)，对其余12个行业组合的平均月度流动性分析发现趋势也存在高度的相似性。

各个行业组合的平均月度流动性描述性统计分析如表(1)所示。其中，平均月度流动性均值最高的是I金融、保险业，最低的是A农、林、牧、渔业；平均月度流动性的标准差最大的也是I金融、保险业，最低的是D电力、煤气及水的生产和供应业。

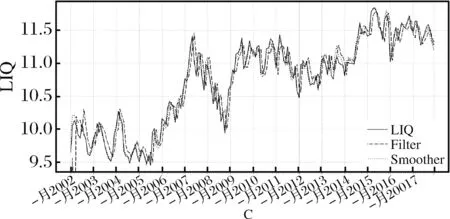
图1 行业组合C制造业的平均月度流动性以及Model 1 Kalman滤波与平滑结果

表1 13个行业组合的平均月度流动性描述性统计量

另外，市场的活跃程度也可由平均月度流动性反映出来：比如2004年1月1日至2004年12月31日，当时，市场已长期持续低迷且股指仍处于下降通道中，市场信心受到了严重的打击，处于典型的“熊市”状态；2006年10月至2007年9月,当时股指急速上升，市场信心高涨，演绎了一段史无前例的“快牛”行情。

3.1.2 宏观经济数据

反映宏观经济态势的因素众多复杂，除了总量指标GDP外，还包括投资指标、消费指标、财政指标、金融指标、通货膨胀与通货紧缩等。其中，对股市影响比较大的一些指标主要有GDP、通货膨胀与紧缩、货币供应量、长短期利率、失业率、汇率等。

考虑到月度数据的获取难度和质量、中国股市的实际情况以及参考很多学者的前期研究，我们选用七个宏观经济变量引入模型，分别为宏观经济指数(一致指数)(MI)、进出口总额(TFT)、广义货币供应量(M2)、居民消费价格指数(CPI)、短期利率(活期存款利率)(SR)、长期利率(一年定期存款利率)(LR)和美元兑人民币平均汇率(EX)。

分析中这些宏观经济变量的数据期间也是2002 年1月4 日到2017 年12月31 日，数据来源为国泰安数据库和中经网统计数据库(http://db.cei.gov.cn)。将前四个变量取对数处理。

首先，对各个变量之间的相关性分析发现，宏观经济变量之间存在着一定的相关性。比如，进出口总额和货币供应量之间的正相关性高达0.930，汇率同货币供应量和进出口总额之间存在较高的负相关性，汇率与短期利率也有着较高的正相关性。因此，这些变量之间存在信息上的重叠，对其进行相应的主成分分析是必要的。

主成分分析结果显示，在选择了前两个主成分后，累计贡献率达到87.1%，所以我们选择前两个主成分加入模型。

3.2 模型的估计结果分析

针对本文提出的模型，运用Kalman滤波与平滑对模型进行估计。滤波用的是t时刻之前的数据，平滑用的是1,…,T时刻所有的信息。

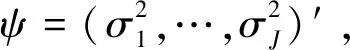
得到的三个模型的参数向量极大似然估计部分结果见表(2)。比较Model 1和Model 2的对数似然值，我们发现当增加了一个潜在的动态因子后对数似然值增加了1820.66。这表明如果对流动性的建模只依赖较小的观测到的协变量集合，那么一个缺失这样的隐变量的模型会存在较大的偏差。

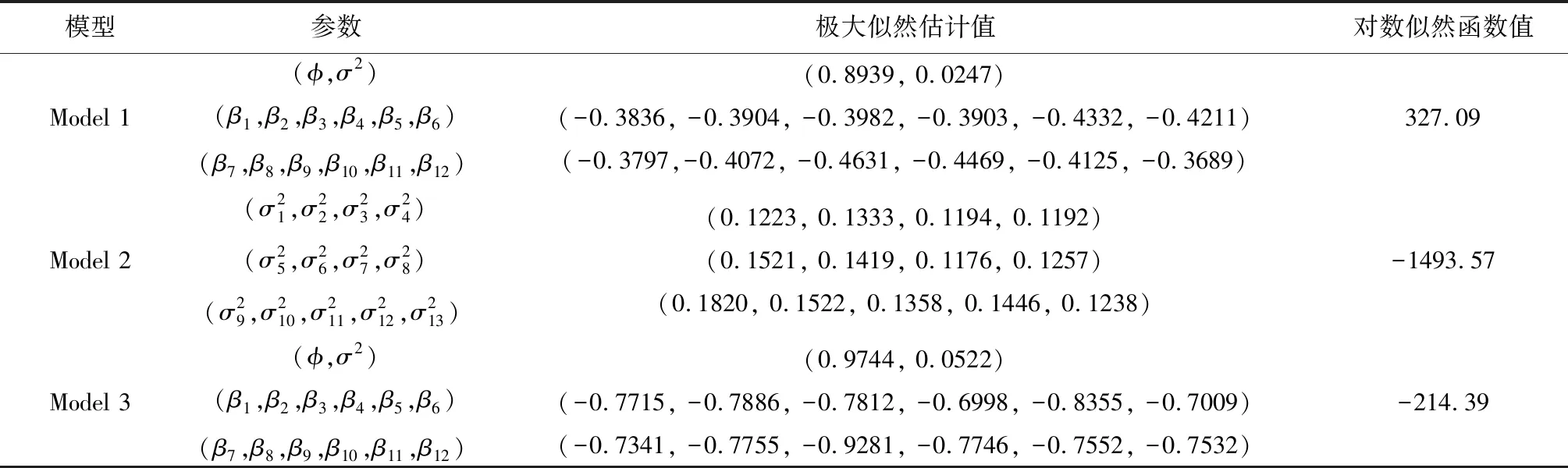
表2 三个模型参数向量极大似然估计结果

Kalman平滑后，以行业组合C制造业为例，Model 1的行业组合C的滤波与平滑结果见图(1)。Model 1 13个行业组合各自的拟合平均相对误差见表(3)。

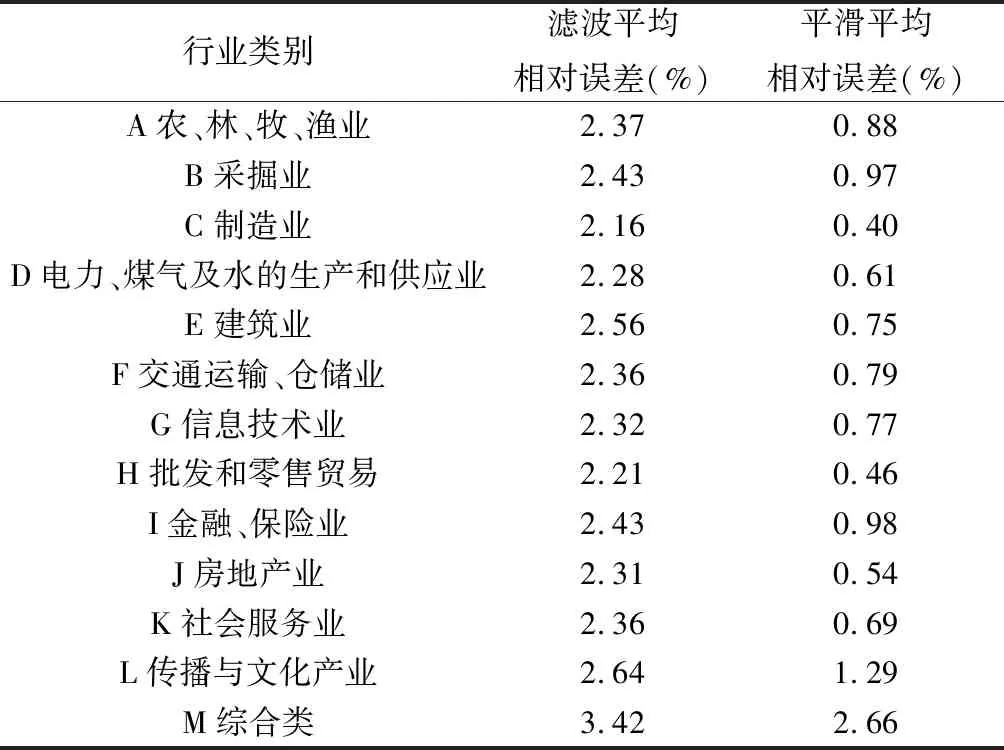
表3 Model 1拟合平均相对误差

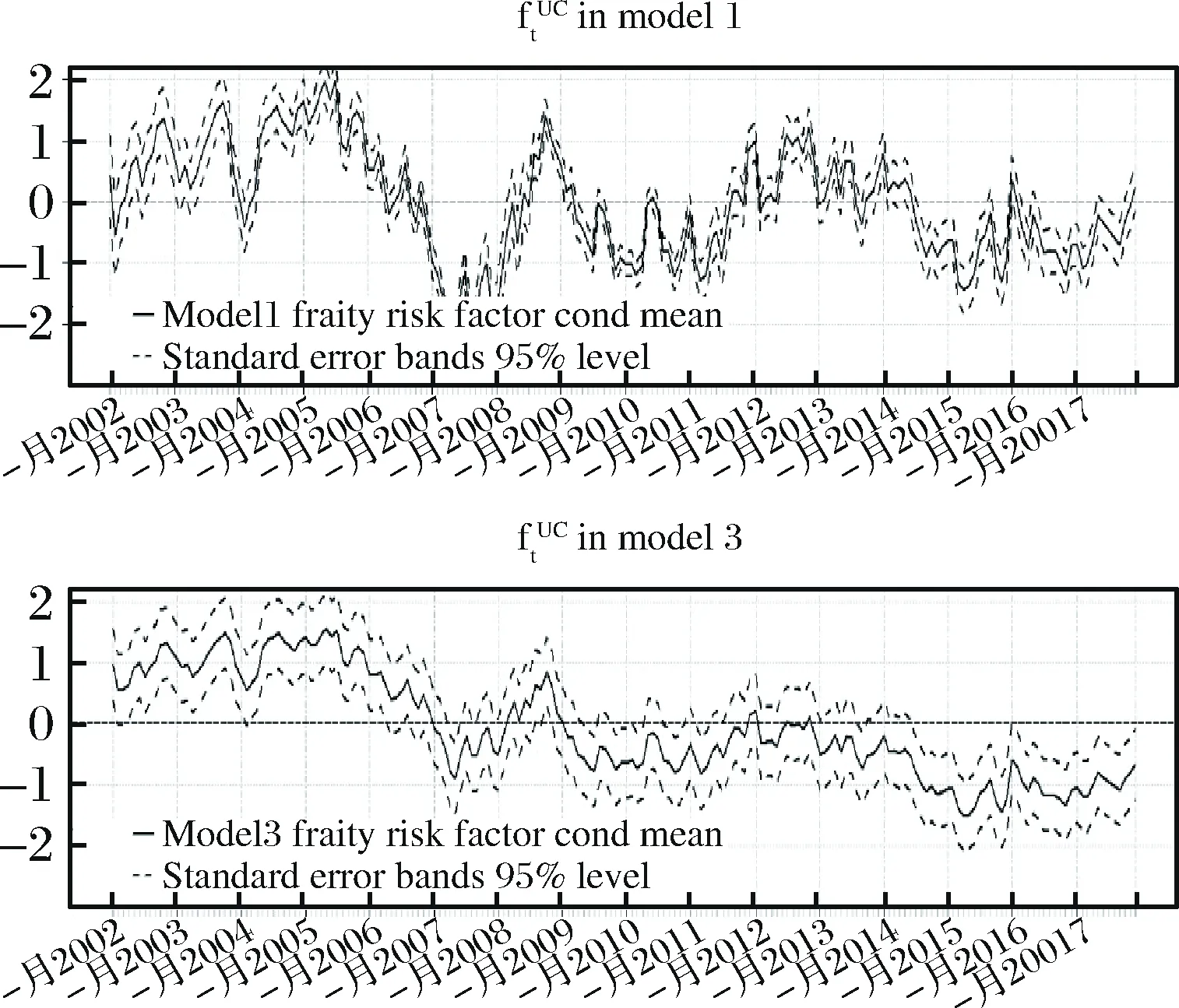
图2 Model 1与Model 3中潜在因子 的Kalman平滑估计及其置信带

Duffie等[20]提出对于银行信用风险管理中的违约概率的建模，潜在因子的引入能够捕捉到遗漏的相关宏观金融协变量以及另外遗漏的难以度量的影响。Koopman等[13]的研究结果表明在超过100多个宏观变量的84%的变动被宏观因子捕获后，潜在因子仍能捕捉到另外遗漏的影响的主要部分。这些潜在因子捕捉了不同时期的不同遗漏影响，而不是一个简单的缺失的协变量可以替代的。我们将这个思想引入股票市场流动性的建模中，发现也有同样的效果。

3.3 样本外预测精度

我们考察之前的三个模型，比较它们的样本外预测表现。准确的预测在风险管理中非常有价值，比如流动性风险可用于股票定价。同样，样本外预测对于建模与时间序列分析都是一个严格的诊断检测。我们展示样本外预测研究，将2017年作为预测区间，2002年1月到2017年某个月份之前的所有数据作为样本数据来估计模型的系数并计算下个月的股市横截面流动性的一步预测。例如，为了预测2017年3月份的流动性，我们将2002年1月到2017年2月份的所有数据作为样本来建模预测。通过这样的方法，我们计算最后一年(即2017年)的12个月份各自的预测，并与真实数据作比较。

我们考虑下面两个衡量准侧：平均绝对百分比误差(MAPE)和均方根百分比误差(RMSPE)

(12)

RMSPE(t)

(13)

其中，j=1,…,J表示行业组合分类。

4 结语

流动性是证券市场的效率所在，较低的流动性会增加交易成本，延长成交所需要的时间，本文主要研究影响宏观因素对股票流动性的建模，试图发现这些因素对于股票流动性有何影响。我们提出的这个新颖的带回归效应的高斯面板数据时间序列模型用来分析和预测股市的流动性风险。这个动态模型结合了用主成分的方法从大量宏观经济协变量中提取出来的因子。在实证研究中，我们发现即使控制了超过80%的宏观经济金融协变量的方差后，引入动态的潜在因子仍有着很重要以及显著的作用。所以，这个潜在因子对于防止流动性估计的偏差是需要的。我们的结果表明，这个潜在因子的存在可能不是由一些遗漏的宏观经济协变量所决定的，而似乎可以捕捉到不同时期不同的遗漏的效应。样本外预测也表明了同时包含宏观因子和潜在因子的动态模型具有良好的表现。

表4 各个模型样本外预测误差(%)