一类具有不同传染力的SEI1I2R传染病模型

黄忠乾，罗 勇，刘本莹

(温州大学数理与电子信息工程学院，浙江温州 325035)

某些疾病的传染力一方面取决于体内所含病毒的水平，例如登革热、乙肝、HIV，另一方面取决于染病者个体与易感者群体之间的接触力度，例如肺结核患者因交际活动与不同范围易感群体接触造成不同程度传染.对于前者，相关文献提出了一类具有不同传染力的艾滋病模型[1-2]、染病者具有不同传染力的SI1I2R模型[3-4]，对于后者的相关研究较少.

基于上述模型的机理和传染病动力学模型及控制策略[3]，本文考虑带有人口迁入、具有不同传染力且加入潜伏期的传染病模型，传染率为非线性，R治愈者终身免疫，建立SEI1I2R传染病模型.模型的基本假设和建立如下：

1）易感者被传染进入潜伏期，经历潜伏期后成为具有不同传染力的I1、I2两类染病者，治愈后终身免疫；

2）单位时间内人口的迁入数量A均是易感者；

3）第Ii类染病者的死亡率为

4）种群的自然死亡率为μ；

5）第Ii染病者的治愈率为

6）潜伏者有可能成为第Ii类染病者的概率为

8）S,E,I1,I2,R分别为易感者、潜伏者、I1类染病者、I2类染病者、治愈者仓室.

在上述假设下的传染病传播仓室图见图1，建立模型如下：

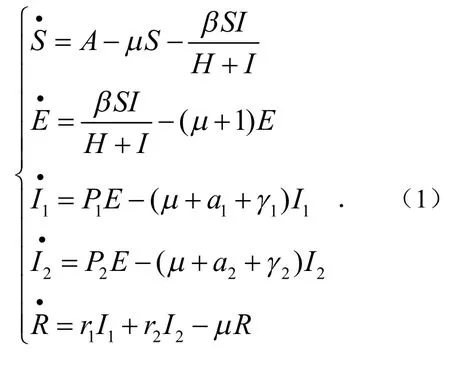
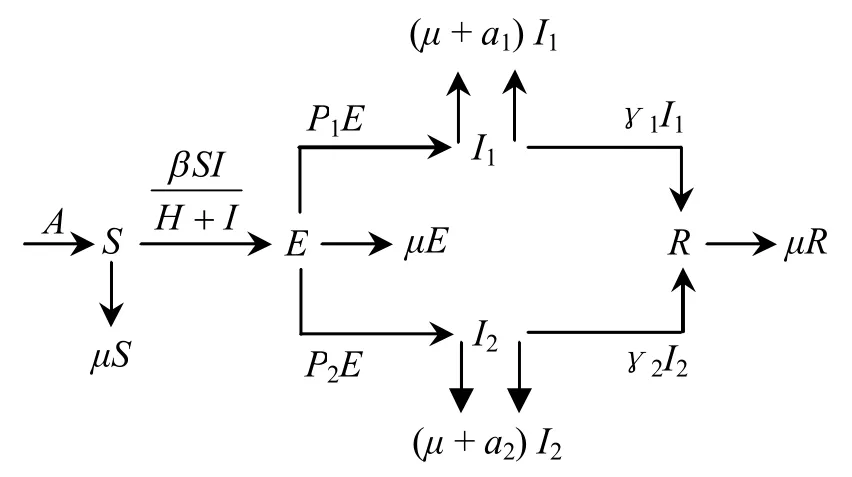
图1 传染病传播仓室Fig 1 The Propagation Chamber for Infectious Disease

1 无病平衡点的稳定性

由于模型的前4个方程没有出现R(t)，故只考虑下面模型：

将模型（2）的4个方程相加可得到：

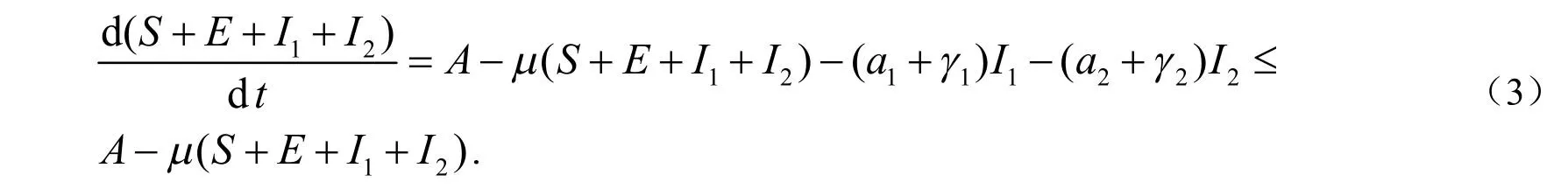
证明：P0的存在唯一性显然.下面构造基本再生数[5]，令矩阵

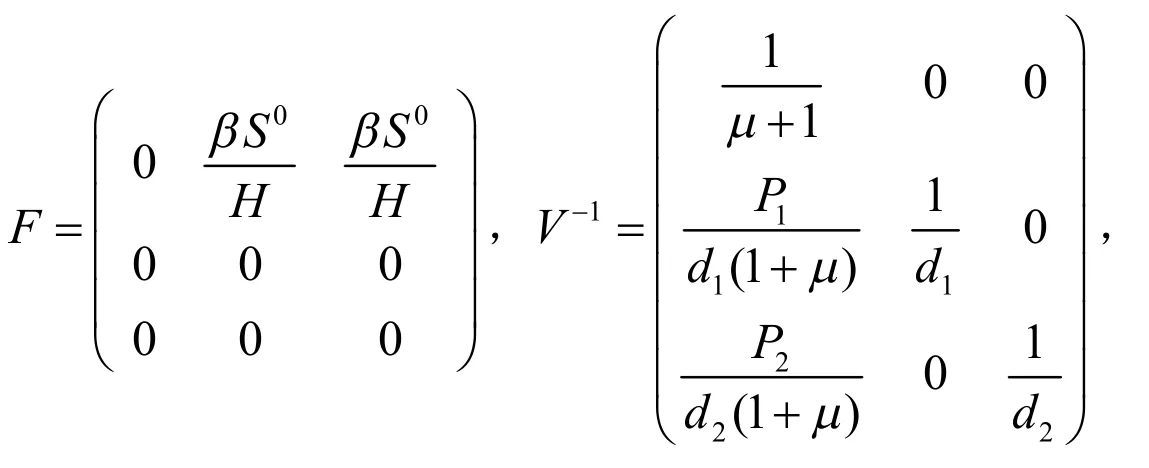
从而再生矩阵[6]故有：

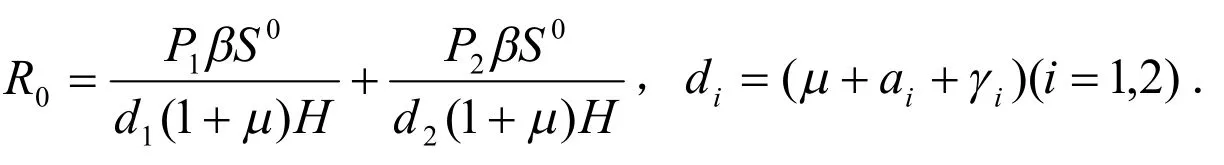
定义1[7]考虑系统令B是g(w)在平衡点w0处的Jacobian矩阵.若矩阵B的所有特征值都小于零，则系统在平衡点w0处局部渐近稳定；若矩阵B的所有特征值都大于零，则平衡点w0不稳定.

引理1[8]考虑多项式方程所有根具有负实部的充要条件是：其中j>n时，补充定义

证明：系统（2）在P0处的Jacobian矩阵为：

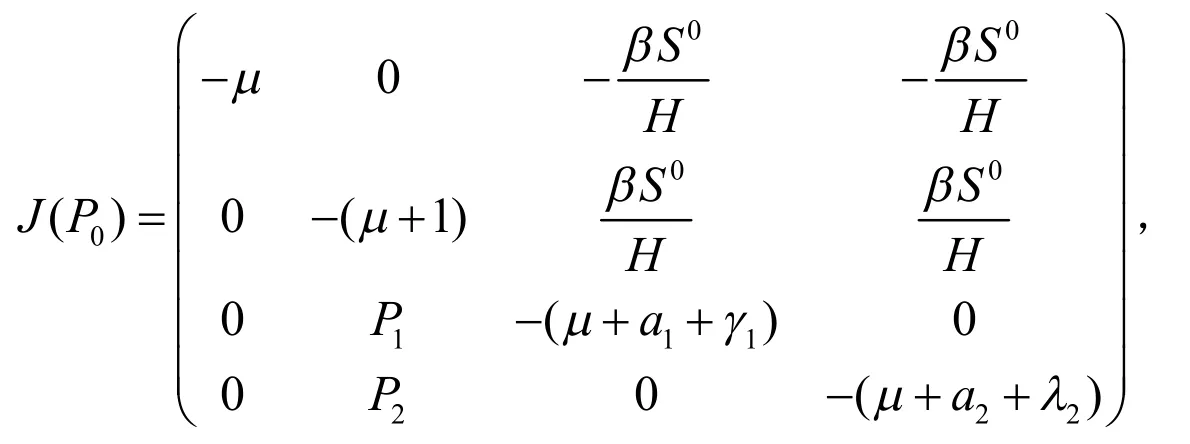
显然λ=-μ是的一个特征根，的其余特征根，由方程决定，其中c1=(1+μ+d1+d2)>0，c2=[d1(1+μ)+d2(1+μ)+d1d2-P1a-P2a]>0，c3=

由引理1可得：

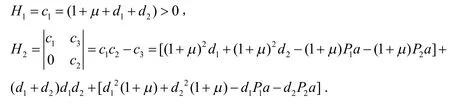
由于R0<1，也就意味着：

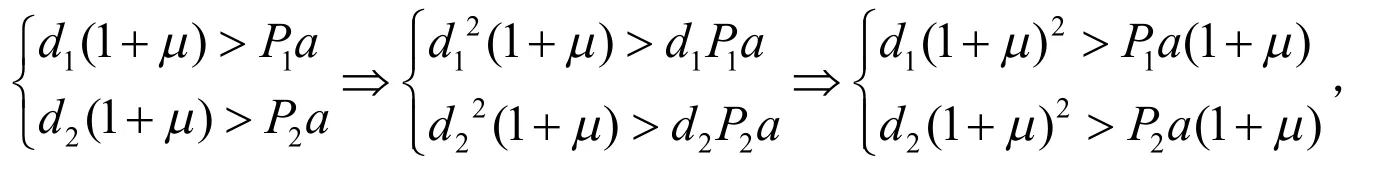
因此，H2>0.

由H2>0可得

由定义1得证，当R0<1时，无病平衡点P0是局部渐近稳定的，相反R0>1时不稳定.

由模型（2）求最后两个方程可得：

把（4）式代入模型（2）的第二个方程可得：

把（4）式和（5）式代入模型（2）的第三个方程有：

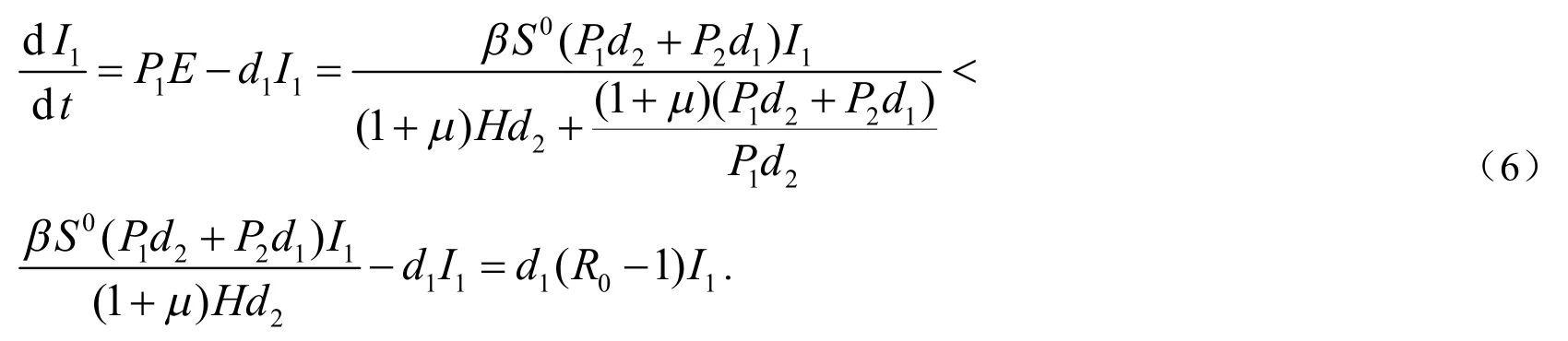
当R0<1时，（6）式右端d1(R0-1)I1<0，由微分方程的性质知：

R0>1时，（6）式右端d1(R0-1)I1>0，I1(t)不收敛，即I1(t)不稳定.

同理可得，R0<1时，

相应地有：

故R0<1时，无病平衡点是全局稳定的，R0>1时，无病平衡点不稳定.

2 地方病平衡点的稳定性

模型（2）的地方病平衡点P*=(S*,E*,I1*,I2*)是方程

在集合Γ内的解，其中di=(μ+ai+γi)(i=1,2).

通过计算可以得到：

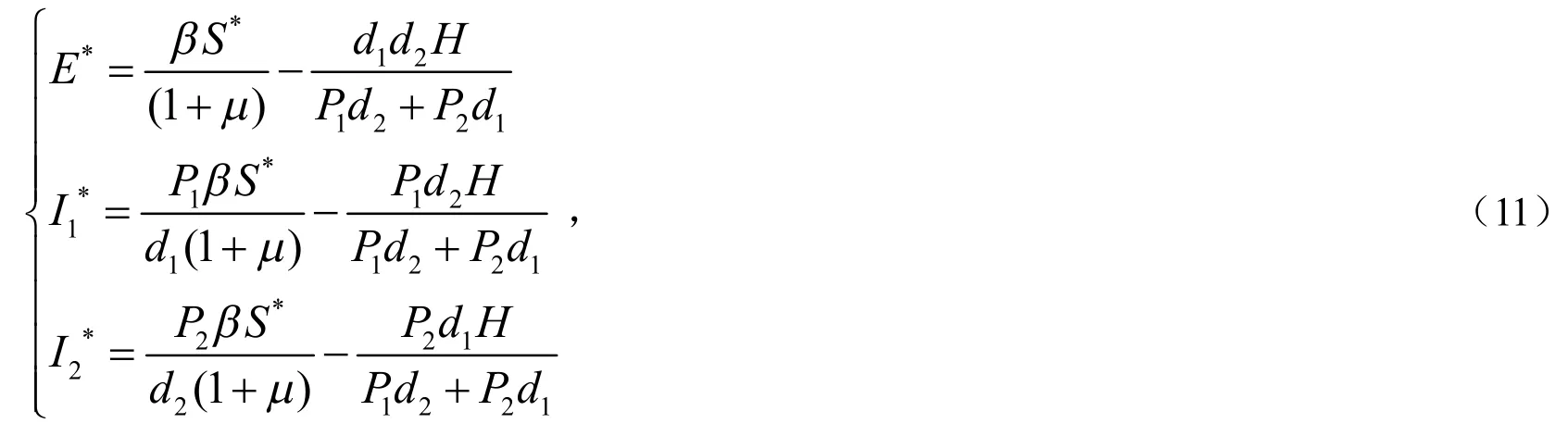
S*可通过求得，F(S)为递增函数，且因此当且仅当R0>1时方程F(S)=0有唯一的根S*.

定理3 对于模型（2），当R0>1时，无病平衡点P*是局部渐近稳定的；R0<1时，无病平衡点P*是不稳定的.

证明：系统（2）在P*处的Jacobian矩阵为：

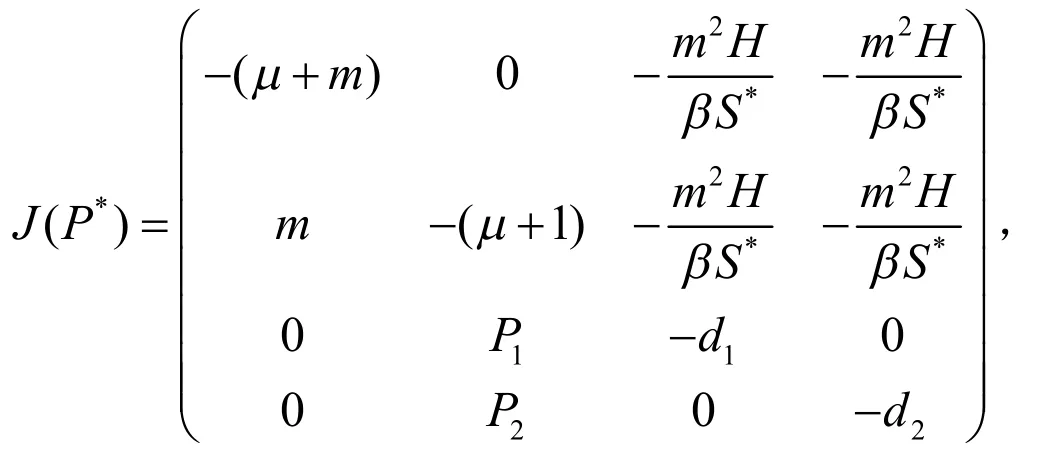
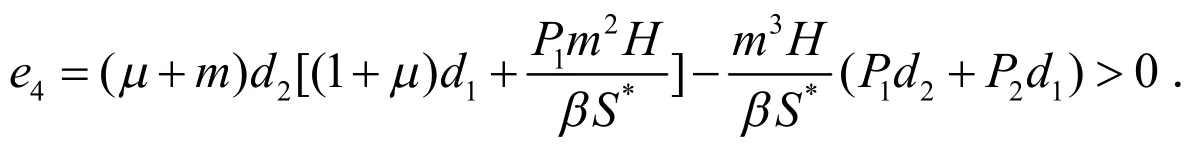
由引理1可得：

由定义1得证，当R0>1时，无病平衡点P*是局部渐近稳定的；相反R0<1时不稳定.

3 结论

本文提出并研究了带有人口迁入、具有不同传染力的SEI1I2R传染病模型，且传染率为非线性对模型（2）求出了基本再生数得出结论：当R0<1时，无病平衡点P0在Γ内是全局渐近稳定的，疾病最终消亡；当R0>1时，存在地方病平衡点P*且是局部渐近稳定的，即传染病会持续存在.