一类广义Camassa-Holm方程解的持续性
2019-06-04李秀歌郭正光
温州大学学报(自然科学版) 2019年2期
李秀歌,余 闯,郭正光
(温州大学数理与电子信息科学学院,浙江温州 325035)
本文将考虑方程
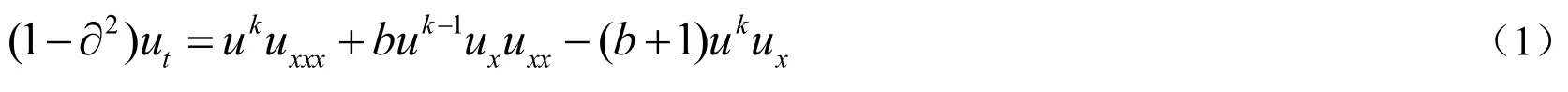
当b=3k时的强解在加权空间中的持续性质,研究思路来源于Guo和Zhou等的一些工作[1-4].文献[1]证明了带有色散项的方程解的持续性质,文献[2]证明了具有两个分量的Camassa-Holm方程解的持续性质,文献[3]证明了Camassa-Holm方程解的持续性质,文献[4]证明了Novikov方程解的持续性质,通过构造加权函数以及利用Young不等式和Hölder's不等式对方程进行估计来获得研究结果.
我们试图找到一类满足下面条件的权函数φ(Weight Function):
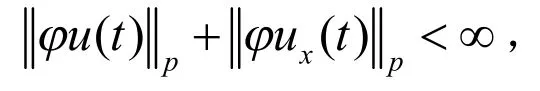
首先介绍一些时间频率分析[6-7]的标准定义和基本结果.
1 一些重要定义
在文献[4]中已经证明φ是ν稳定的当且仅当加权的Young不等式


2 主要定理

其中常数C依赖于函数v,φ和
容许权函数的经典例子是

3 定理证明
证明:为了计算方便,改写方程(1)为下面形式的运输方程:

对于3k=b,我们有对于任意的我们定义截断函数:
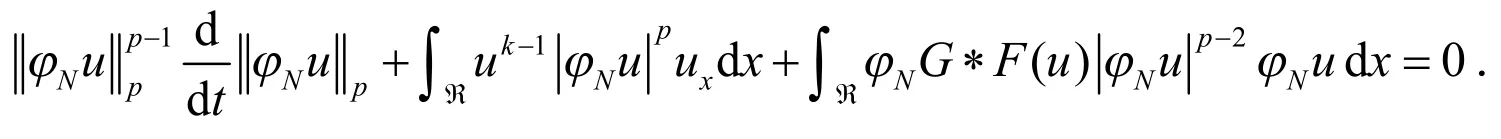
注意到

由Hölder's不等式得到

结合方程(2)和(3)得到
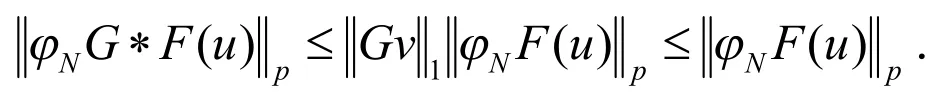
因此有

对方程(4)关于变量x求微分,得到:
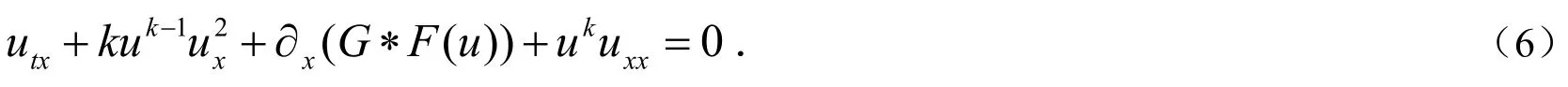
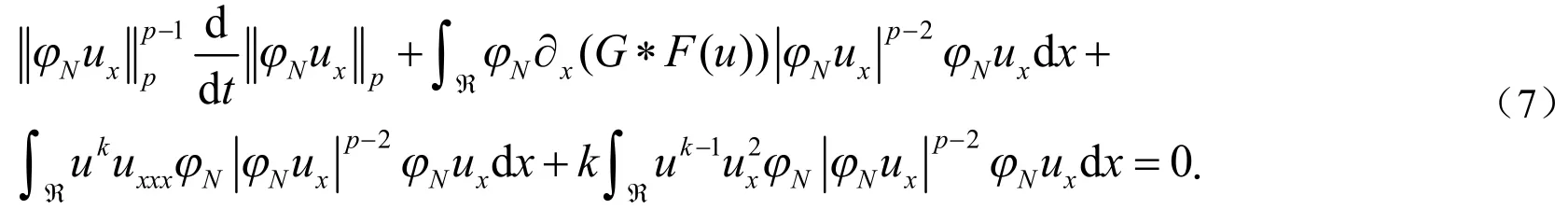
对(7)式左边第三项进行如下估计.首先,对第三项变形
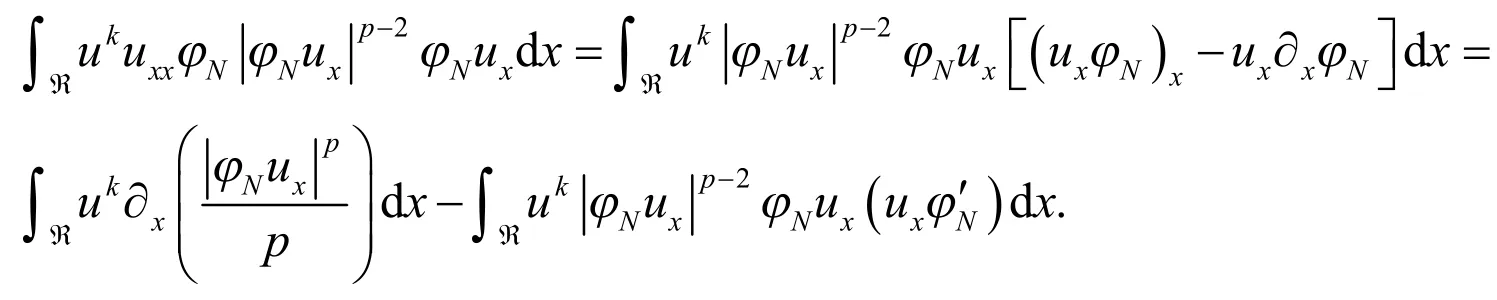

(7)式第四项变形为:

并且,(7)式第二项为:
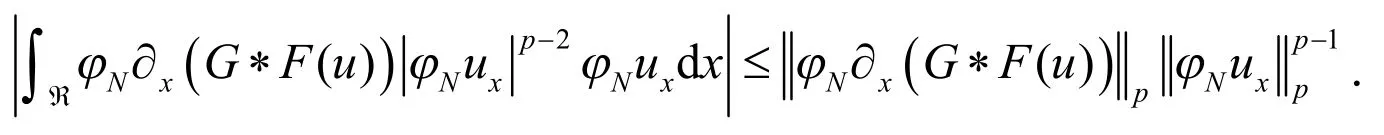
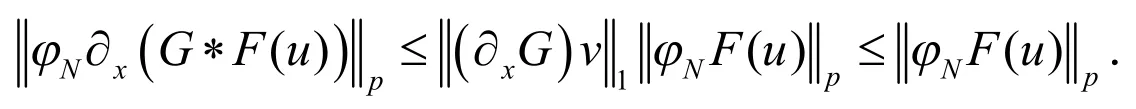
得到

此外,通过F(u)的定义很容易得出:

结合方程(5)、(8)和(9),则存在常数C满足
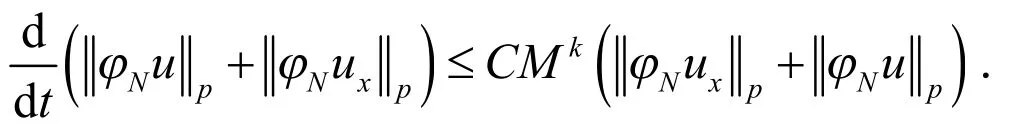
利用Gronwall不等式,就有

定理的剩余部分只需证明p=∞,因为所以对于任意的q≥2,类似前面讨论可以得到