渗透建模思想 助力学习升温
2019-06-03张文雅
张文雅
摘 要:在小学数学教学中渗透数学模型思想,是课程改革所赋予的重大使命。因此,在具体的教学活动中教师应善于创设问题情境、搭建猜想验证平台、给予实践应用机会,帮助其感知模型,建构模型。同时,还应引导学生运用掌握的数学与模型去分析问题、研究问题,在应用中不断提高学习数学的兴趣和应用意识,让数学学习持续升温。
关键词:模型思想;问题情境;小学数学;学习升温
培养和发展学生的模型思想是数学教学的十大核心任务之一。因此,在小学数学教学中教师就应重视建模思想在教学中的渗透,着力通过帮助学生感知数学与现实真实之间的联系,促使他们在具体的生活化情境中或问题情境中发现规律,进而帮助他们逐步形成初步的数学思维模型。在此,笔者结合“平行四边形的面积”的教学实践,谈一谈怎样引领学生从问题情境到建立模型,再到验证求解等学习体验中建立数学模型。
一、创设问题情境,引发学习体验
帮助学生建立数学模型,问题是先导。也正是问题的引领,才能激发学生探究的欲望,产生真正的学习需要,让他们的学习充满活力。所以在教学中教师要善于解读教材文本的内涵,精准地把握学生生活现实,进而创设符合学生学习需求、心理需求的情境,让他们能快乐学习、智慧学习。
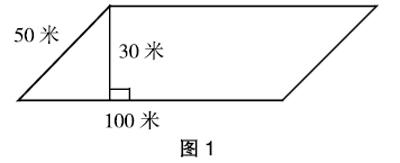
如,在学生较为熟练地解决了长方形、正方形的面积计算问题后,教师就可以顺势推出:请看一看这块菜地(图1),说出它的名称,想想这个菜地的面积是多少平方米?
创设这样的情境,旨在让学生在长方形面积、正方形面积计算的经验支持下,进行一定的探索与猜想。同时,还利用这个问题引发学生关注学习,促使他们的学习思维发散开来。
当然,要让学生顺利地、正确地去解决这个问题,还需要学生建立平行四边形面积计算的思维模型。尽管长方形、正方形都是平行四边形,但是它们的面积计算方法与经验、思维对一般性的平行四边形是不适用的,数学模型也是不匹配的。所以就得给予一个探究平台,让他们能够提出猜想,想到方法去验证猜想,进而在思维碰撞中建构平行四边形面积计算的模型。
二、引领猜想验证,加速学习建模
要实现学生高效的数学学习,教师就得重视在问题引领下的猜想、探索、验证等系列活动的开展,以便学生在真实的活动中学会分析筛选,学会抽象概括,进而形成初步地解决问题的模型,使得相应的数学模型得以建立。如上述教师创设的问题情境,其目的就是让学生在猜想、尝试等活动中发现问题,进而实施验证纠偏,以达到理解知识、建构相应的解决问题的数学模型的目的。因此,在上述情境下组织这样的相关学习活动:
一是提供自由探究的平台。首先让学生自己读题、审题,进而尝试。其次组织学习展播,用投影显示学生的思考。有的学生是:50×100,有的学生是:30×50,还有的学生是:30×100。此时的教师不是评价者,而是学生学习争辩的挑唆者。“哦!有3种思考了,还有没有其他的啊?”“既然没有其他的想法,那下面就来研究一下这3种思考,请同类解答的同学先想一想,你是怎么想到这种方法的?”教师没有做出评价,而是要求学生说出自己的思考过程,促使学生再回过头来想一想自己解答的依据是什么。第三组织学习辩论,让事理在思辨中愈发清晰起来。“长方形的面积就是相邻的两边长与宽相乘得到的,所以平行四边形的面积也是相邻两边相乘。”“我认为平行四边形它不像长方形那样,都是直角,但长和宽是互相垂直的,所以用30×50。”“我也是从长方形长和宽互相垂直来思考,这里30和100的边是互相垂直的,所以就把它们相乘了。”
二是保证验证学习的实效。为保证验证的实效性,上述问题只能作为引子,所以教师还得搭建学习实验的平台。“请同学们,用好老师给各小组准备的学具,尝试不同的方法,看看会有什么发现?”学生会在活动的提示下进行着不同的尝试,有的采用方格纸覆盖法,数方格得出给出的平行四边形的面积是24平方厘米;有的采用画正方形小方格的方法,也得出24平方厘米;有的采用剪拼法,任意画一条高,沿着高把平行四边形剪成2块,再移拼成一个长方形,得到面积也是24平方厘米……
学生活动是开放的,方式是多样的,但绝大多数的结果是24平方厘米。尽管这样,教师还得组织验证方法的比较,学生会在思辨中发现“把平行四边形沿高剪下,再移拼成长方形,方法最直接,也最容易看出。”因为是剪下一部分,再移拼,所以图的形状会改变,但面积是不会变的。同时还发现,平行四边形的底就是长方形的长,平行四边形的高就是长方形的宽,从而直接推导出“平行四边形的面积=底边×高”,平行四边形面积计算的数学模型也就在争辩中脱颖而出。
从中不难发现,只有当学生经历过问题感知、想象猜测、比较分析、验证猜想、归纳提炼等系列活动,他们才能更加理智地区分猜想的对错,从而建立牢固的理性感悟。并在此期间,有效地建立起有关问题研究的正确的数学模型,实现学习的有效突破。
三、营造体验氛围,引导应用模型
任何一种知识都需要在实践中加以巩固和深化,这样才会形成对应的技能。同理,当学生形成了初步的数学模型,但不能说他已经掌握了该思维模型,教师还得营造一个个体验数学模型的氛围,让学生在解决问题中真正消化学习,正确理解,从而科学建构。
如,在上述的验证中学生基本感悟了平行四边形面积的思维模型,明白“平行四边形的面积=底×高”,这还不够。还需要教师为他们设计用模型的平台,让他们在真实的情境中深化理解模型,在运用中进一步熟悉模型。
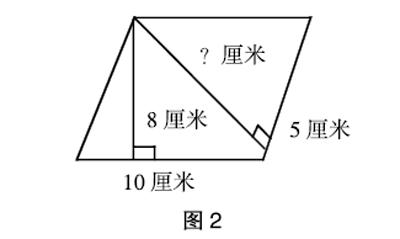
比如,设计三组训练:一是基本题型,给定底和高计算面积。二是解决类似导入部分的问题,学会甄别,科学应用模型去思考问题。三是稍有拓展的习题:如图2,计算出图中未知的高是多少厘米?
设计三类应用训练,主要目的就是让学生在不同的情境中灵活地运用该模型,学会分析思考,以促進他们的数学思维得到训练,他们的解决问题的能力得到发展。同时,也有助于学生进一步理解数学模型,促进数学模型的内化。
总之,在小学数学教学中渗透数学模型思想是一项复杂且艰巨的工程,还需要教师在具体教学中科学渗透,精准引领,促使学生更好地建构数学模型。同时,还要创设应用平台,促进数学模型在学生的学习深入中不断升华,逐渐内化。
