干涉实验中光场分布的计算及可视化
2019-06-03吴云虎
吴云虎
(扬州职业大学, 江苏 扬州 225009)
在干涉实验及其派生技术的教学和研究中,经常需要通过理论计算或实验测量法分析干涉光场分布[1]。而相关文献和教材中干涉实验图样基本是影印,特征虽明确但难以明晰其内在变化规律[2]135-153。通过数学计算干涉图样耗时费力,又不易专注精力于对干涉特征和规律的探索。在实验中若能优化复杂繁琐的数学计算,观察到特征明显的物理实验现象,掌握明晰现象背后存在的规律,是提高物理实验教学效率的关键。Wolfram公司的Mathematica软件强大的符号运算、数值处理和图形绘制功能,在实验室物理模型建立和数据可视化过程中具有独特的优越性[3-4]。本文通过Mathematica 11数值运算使杨氏双缝、等倾和牛顿环干涉实验的光场分布可视化,为实验室光学干涉的特征和规律分析提供策略与手段,实验教学效率和实验真似度得到有效改善。
1 Mathematica基本指令格式规范
在干涉实验设计过程中,将实验特征和规律可视化的指令分别整合到Manipulate交互指令模块内[5]263-289,便于学习者在实验操作界面上自行调试并观察实验的特征和规律。因此,干涉实验特征可视化设计和指令格式规范为
Manipulate[SliceDensityPlot3D[I(x,y,z,p1,p2,…),{x==x0},{x,xmin,xmax},{y,ymin,ymax},{z,zmin,zmax}],{p1,pmin,pmax},{p2,pmin,pmax}…]
(a)
格式规范(a)中使用了SliceDensityPlot3D切片绘图指令在x=x0,ymin≤y≤ymax,zmin≤z≤zmax平面区域绘制出光场强度I(x,y,z,p1,p2,…)的三维密度图。借助Manipulate交互指令可以调试指标参数p1,p2,…,并观察指标参数阈值下干涉实验的光场强度分布特征。同样干涉实验规律可视化设计和指令格式规范为
Manipulate[Plot[Table[r(p,p1,p2,…),{p1,pmin,P1},{p2,pmin,P2}…],{p,pmin,pmax},Epilog→Table[{Inset[Row[{“p1=”,p1}],{p,r(p,p1,p2,…)}],…},{p1,pmin,P1},{p2,pmin,P2}…]],{P1,Pmin,Pmax},{P2,Pmin,Pmax}…]
(b)
格式规范(b)中使用了Plot平面绘图指令绘制纵向数据系列为r(p,p1,p2,…),横向数据系列为p的数据线。指标参数p1,p2,…阈值不同情况采用不同数据线绘制在同一绘图区内,并对数据线的指标参数阈值采用数据标注以示区分,采用Inset插图指令在(p,r(p,p1,p2,…))处标注出p1名称和数值。借助Manipulate交互方式调试P1,P2,…可以控制指标参数p1,p2,…上限范围,并能够观察到在更宽广指标参数阈值区间内干涉实验的光场变化规律(主要观察对象为明暗条纹)。在干涉实验光场分布特征和变化规律的图形可视化过程中,配合使用绘图附属的增强效果选项,如边框样式、坐标轴样式、绘图样式等设置,就可以设计出更加美观规范的图形界面,所用规范可参考Mathematica软件指导手册[6]。
2 杨氏双缝干涉实验
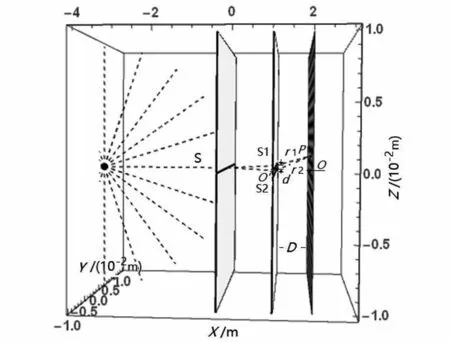
图1 双缝干涉实验指标参数及光场分布特征

(1)
各级明纹或暗纹与屏中心O距离
z=z(d,D,λ,k)
(2)
S1和S2相干光场强度[2]88-91
(3)
将计算出来的I(z,d,D,λ)和z(d,D,λ,k)分别代入格式规范(a)和(b)。设I0为1,选取双缝间距d=0.0004~0.0006m,屏缝距离D=1.0~2.0m(特征量:1.0m,1.5m,2.0m),相干光波长λ=410~660nm(特征量:457nm,589.3nm,632.8nm)为参数指标,如图1所示调试I(z,d,D,λ)中参数指标数值,在Z轴z=-0.01~0.01m范围内可以观察到干涉条纹分布均匀,相邻明纹或暗纹间距相等的基本特征。图2选取衍射级数k=0~3,对条纹中心距离z(d,D,λ,k)数据线进行观察分析,可以明确获知z(d,D,λ,k)对d、D、λ及级数k之间的数学比例关系。
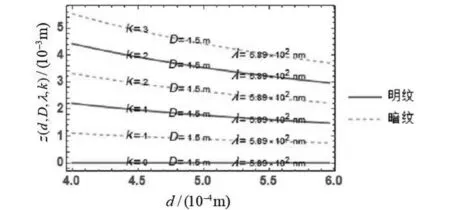
图2 双缝干涉实验条纹中心距离z(d,D,λ,k)的变化规律
3 等倾干涉实验
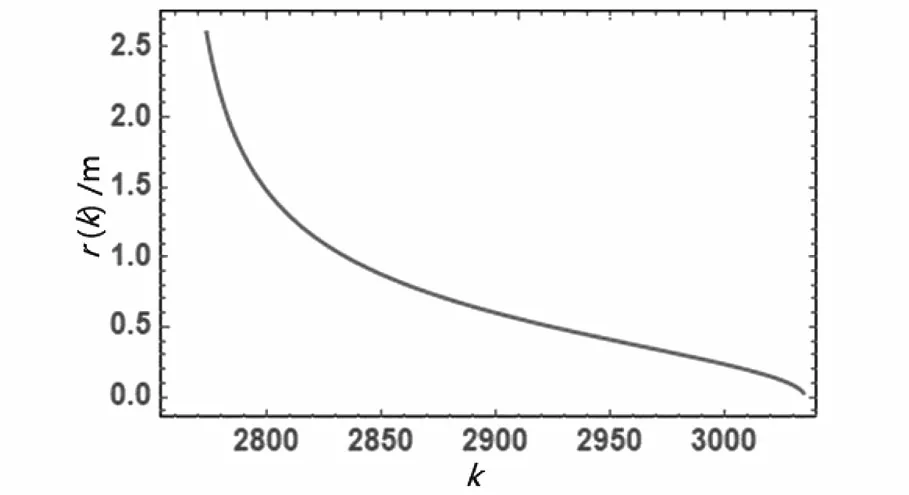
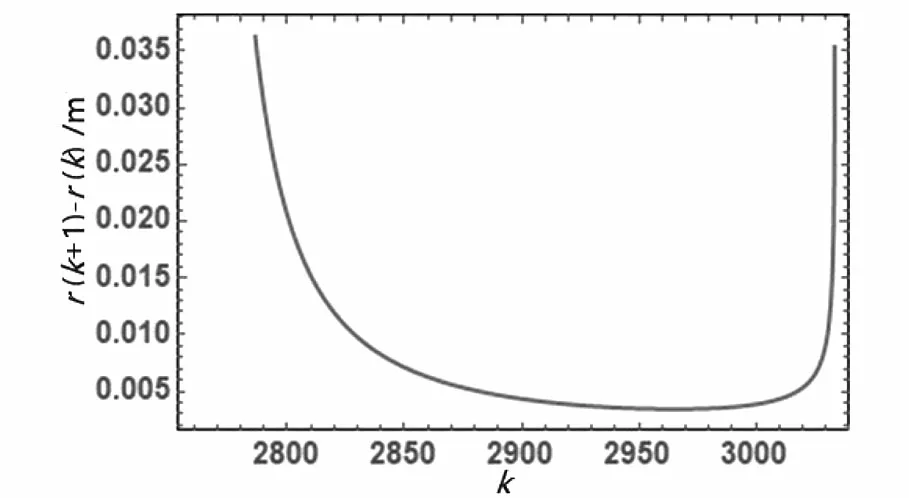
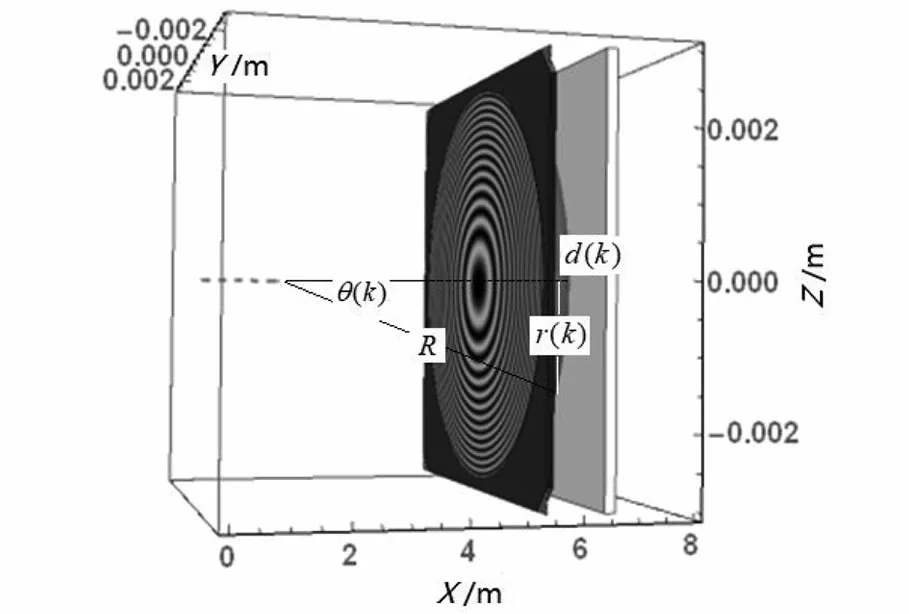
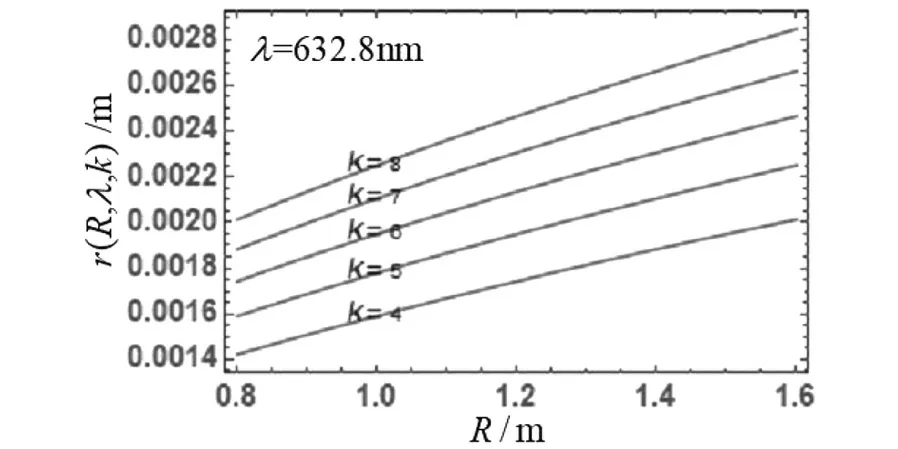
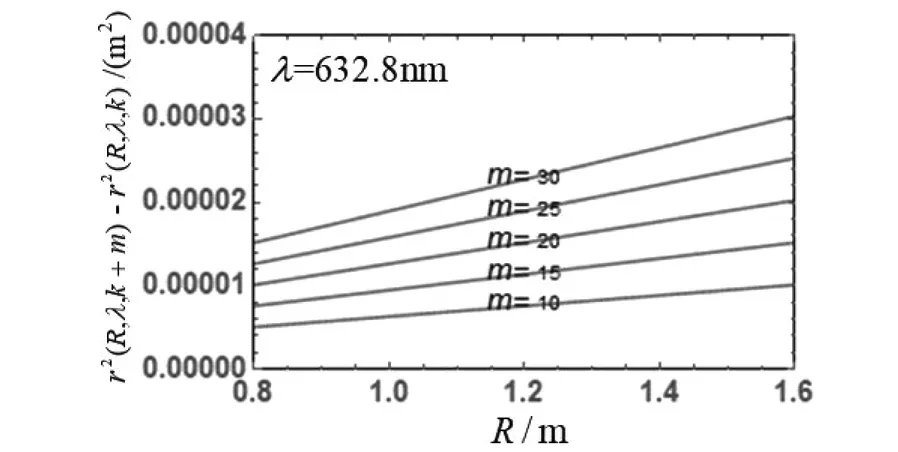
实验室中普通单色光λ以入射角i进入厚度为d,折射率为n(空气折射率n1 图3 等倾干涉实验指标参数及光场分布特征 相干平行光的光程差(上表面有半波损失)、明纹及暗纹干涉级数为 (4) (5) 以薄膜法向为会聚透镜主光轴(X轴)方向,由式(4)推导出干涉级数为k的条纹在焦平面上中心距离 r(k)=ftani (6) 相干光场强度 (7) 将计算出来的I(y,z)代入格式规范(a),r(k)和r(k+1)-r(k)分别代入格式规范(b)。设I0为1,选取透镜焦距f=0.60m、相干光波长λ=632.8nm,薄膜介质ZnS折射率n=2.4,空气折射率n1=1,薄膜厚度d=0.0004m为参数指标,如图3所示在y=-0.2~0.2m,z=-0.2~0.2m范围内可以观察到干涉条纹间距r(k+1)-r(k)分布不均匀,呈现中心疏,边缘密的基本特征。观察分析图4等倾干涉r(k)数据线。 (a)条纹中心距离r(k)与级数k的关系 (b)相邻条纹间距r(k+1)-r(k)与级数k的关系图4 等倾干涉实验条纹中心距离、相邻条纹间距的变化规律 条纹中心距离r(k)随级数k增加而非线性递减。焦平面上干涉级数中心高,边缘低;对等倾干涉r(k+1)-r(k)数据线观察分析可知,相邻条纹间距r(k+1)-r(k)变化存在拐点k0,中心级到k0区间快速递减,k0外侧区间缓慢递增。 实验室中普通单色光λ垂直照射放置在平板玻璃上曲率半径为R平凸透镜,在透镜下方空气膜层上下表面反射形成相干光,如图5所示。两束相干光光程差(下表面有半波损失)、明纹和暗纹干涉级数为 图5 等厚干涉实验指标参数及光场分布特征 (8) 从中心向边缘区域(Y-Z平面)光程差δ每增加λ/2,就依次出现明或暗的条纹。根据几何关系计算出k级条纹中心距离 r(k)=r(R,λ,k) (9) 相干光场强度 (10) 将计算出来的I(y,z,R,λ)代入格式规范(a),r(R,λ,k)和r2(R,λ,k+m)-r2(R,λ,k)分别代入格式规范(b)。设I0为1,选取透镜曲率半径R=0.8~1.6m,相干光波长λ的457nm,589.3nm,632.8nm为参数指标,如图5所示调试参数可以在y=-0.003~0.003m,z=-0.003~0.003m范围内观察到干涉条纹分布不均匀,呈现中心疏,边缘密,在空气膜厚度相等处形成同级干涉条纹,中心处为暗斑的基本特征。 对图6等厚干涉r(R,λ,k)数据线观察分析可知,从中心0级暗纹向边缘区域干涉级数k增加。条纹中心距离r(R,λ,k)分别随干涉级数k或曲率半径R增加减速递增;对等厚干涉r2(R,λ,k+m)-r2(R,λ,k)数据线观察分析可知,级差为m的两级干涉条纹中心距离的平方差r2(R,λ,k+m)-r2(R,λ,k)分别与级差m和半径R成正比,这也是牛顿环干涉实验测量的理论基础[7]60-65。 (a)条纹中心距离r与透镜曲率半径R、级数k的关系 (b)两级干涉条纹中心距离平方差与透镜曲率半径R、级数k、级差m的关系图6 等厚干涉实验条纹中心距离、具有级差的两级干涉条纹中心距离平方差的变化规律 基于几何光学计算出杨氏双缝、等倾和牛顿环干涉实验光场分布,使用Mathematica软件图形指令进行可视化仿真。在仿真界面上依次调试光场分布解析式中的参数值可以观察到不同阈值条件下光场强度分布的特征。本文在实验中还进一步使用数据线方式可视化了光场分布与指标参数的连续性关系。实践表明,该方法在干涉实验教学中能够做到使学生深刻认识光场分布的特征并系统掌握光场分布的内在规律,提高了教学效率。
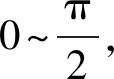
4 牛顿环等厚干涉实验
5 结果与讨论
