基于Tennant法改进的生态水位计算方法研究

吴 玲 玲，闫 中 月，阮 晓 红

(南京大学 地球科学与工程学院水科学系，江苏 南京 210023)

河流生态系统是地表最富生产力和生物多样性的生态系统类型之一，具有极其强大的生态服务功能[1]。科学确定河流生态需水，合理配置水资源供给需求，维持河流系统水的自然循环，对维持河流生态系统健康具有重要的意义。生态需水是在特定时空下，满足河流生态系统诸项功能所需水量的总称[2-5]。目前，有关生态需水确定的方法超过200种[6-7]，归纳起来主要有水文学评价法(Tennant 法[8]、Texas 法[9]等)，水力学评价法(湿周法[10]，R-2 Cross法[11]等)，栖息地评价法(IFIM 法[12]、PHABSIM 法[13]等)及综合法(BBM 法[14]、整体评价法[15]等)。其中，水文学法需要长序列的历史水文数据，其他3类方法需要河湖水力参数及生物响应的数据积累。

由于我国河流生态观测工作起步较晚，相关资料积累不足，国内学者主要采用水文学方法开展河流生态需水研究。其中，应用最多的是Tennant 法[16-17]。Tennant 法是依据观测资料而建立起来的流量和栖息地质量之间的经验关系，取多年平均流量的不同百分数作为河道不同栖息状态下需水量推荐值[18-22]。由于其统计参数为流量，在无流量站点的河流中难以应用。目前，我国水文监测站网尚不完善，许多河流缺少流量站，但水位站的设置较为普遍。水位是反映水文情势的重要指标，与流量往往存在较为明显的相关性[23-24]。在流量资料缺乏条件下，可建立水位与流量、流量与河道生态平衡和生物多样性等的关系，即河流生态水位[25-26]。淮河流域是我国典型的基流匮乏、多闸坝流域，除干流外大多数水文站为水位测站[27-28]。

本文选择淮河流域作为研究区域。首先，选取流域干支流具有长序列历史流量资料的站点，计算Tennant法对应栖息状态下流量比值的保证率，进行四分位数和方差分析，确定淮河流域河流系统不同栖息状态下的水文保证率；然后，将确定的保证率用于计算淮河入海水道的生态水位，以期为缺乏流量资料的河流的生态需水研究提供一种理论计算方法。

1 基于Tennant法改进的生态水位计算方法

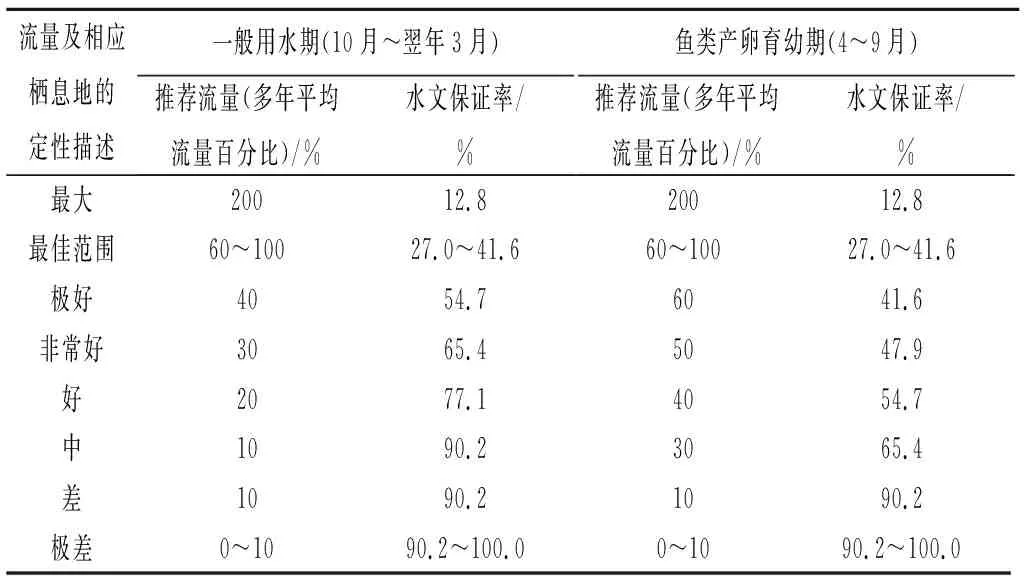
Tennant法又称蒙大拿法，是田纳特( Tennant, D.L )于1976年提出的河流生态需水评估方法。该方法基于1964～1974年间对美国11 条河流实施的详细野外调查实验，分析在不同地区、不同河流、不同断面和不同流量状态下，物理、化学和生物信息对冷水和暖水渔业的影响。进一步将全年分为一般用水期与鱼类产卵育幼期两个时段，建立栖息地质量与流量的关系(见表1)，基于此关系确定不同河流不同栖息等级下的生态流量[18-22]。

表1 Tennant法对栖息地质量的描述Tab.1 Tennant method′s description to habitat quality

本研究在Tennant法的基础上，根据流域内长序列流量监测站点资料拟合皮尔逊Ⅲ型累积频率曲线，然后将各站点Tennant法不同栖息状态的推荐流量代入曲线计算累积频率，以此作为不同栖息状态下的推荐保证率，应用于流量资料缺乏型河流，取对应保证率下水位作为生态水位。具体步骤如下。

(1) 利用P-Ⅲ曲线将Tennant法不同栖息状态下推荐流量比值转换成对应的保证率。

皮尔逊Ⅲ型(P-Ⅲ)累积频率曲线分布函数如式(1)所示：

(1)

(2)

式中，Fδ为不同栖息状态下推荐的多年平均流量倍数的保证率，x为水文指标，此处指流量，δ为不同栖息状态下推荐的多年平均流量倍数，μ为多年平均流量，α、β为皮尔逊Ⅲ型分布的形状尺度参数，α>0，β>0，a0为皮尔逊Ⅲ型分布的位置参数，Cv为离势系数，Cs为偏态系数。

(2) 将多年月均水位Z按照从大到小的顺序进行排列,如式(3)，利用公式(4)进行Pn值计算，然后将Pn与对应的月均水位拟合成频率曲线。

Z1>Z2>…Zi…>Zn

(3)

Pn=n/(N+1)×100%

(4)

式中，Pn为序列n所发生的频率，n为序列号，N为总序列数。

(3) 根据步骤(1)Tennant法不同栖息状态下推荐流量转换的保证率和步骤(2)拟合的频率曲线，计算不同栖息状态保证率下所对应的水位作为生态水位。

ZFδ=Z(Fδ)

(5)

式中，Fδ指保证率，ZFδ指频率分布上对应某保证率的水位。

以淮河流域息县水文站为例，具体计算过程为：根据长序列流量资料拟合P-Ⅲ曲线，计算Tennant法不同栖息状态下推荐流量的保证率，取对应保证率下水位为生态水位。图1中标识了200%推荐流量的保证率为11.9%，图2中对应保证率水位为34.89 m，即为此栖息状态下生态水位。

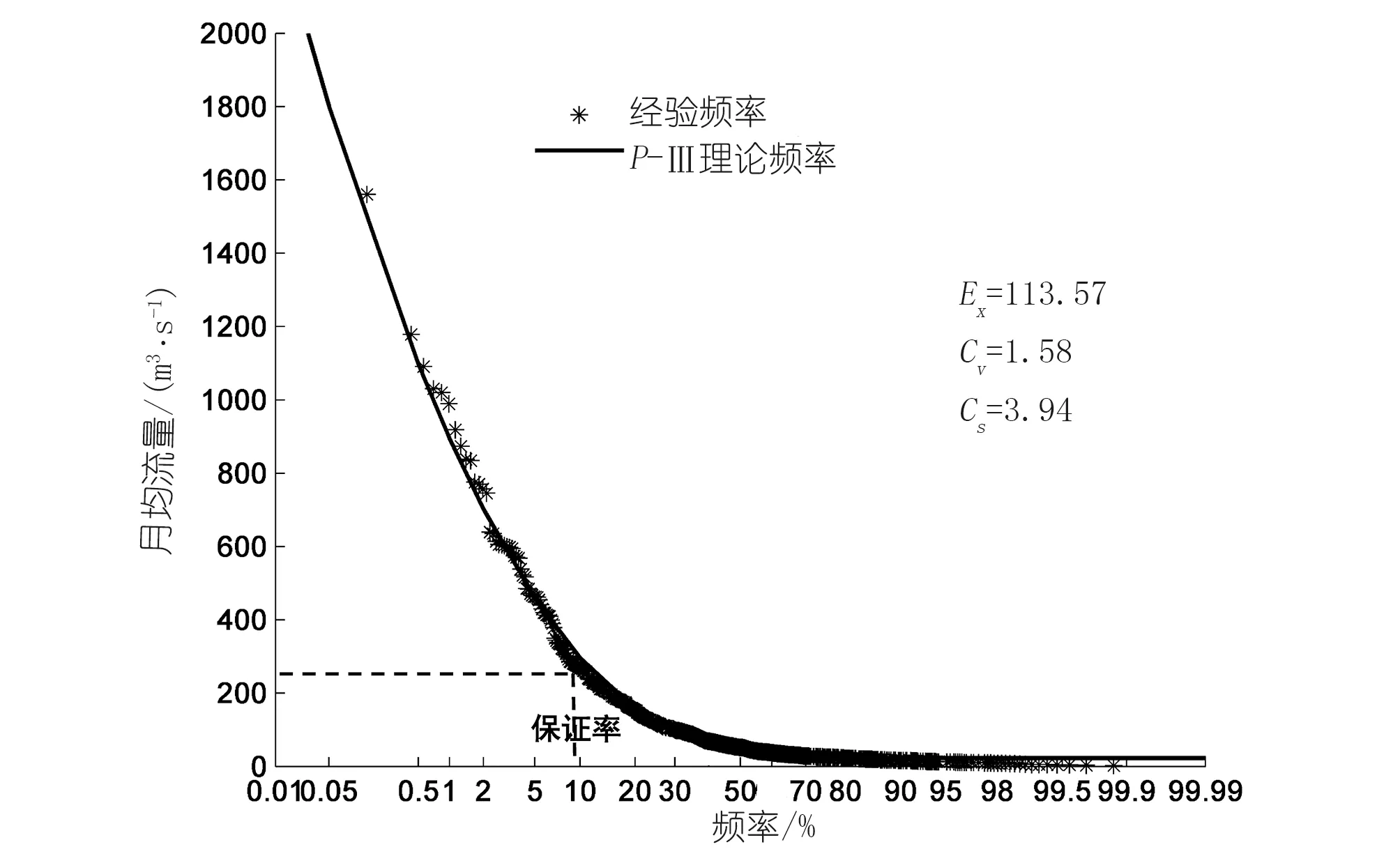
图1 息县水文站流量频率曲线Fig.1 Flow frequency curve at Xixian hydrology station

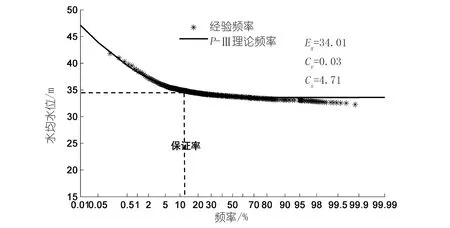
图2 息县水文站水位频率曲线Fig.2 Water level frequency curve at Xixian hydrological station

2 结果与讨论

2.1 数据资料

淮河流域面积为27万km2，流域内除干流外大多数水文站为水位测站[27-28]。因此，建立河流生态水位方法更具有普适性。本文选择了淮河流域主要干支流上具有较长序列流量监测数据的19个水文站作为Tennant法栖息状态下生态流量比值转换保证率的参考站点，具体分布如图3所示。

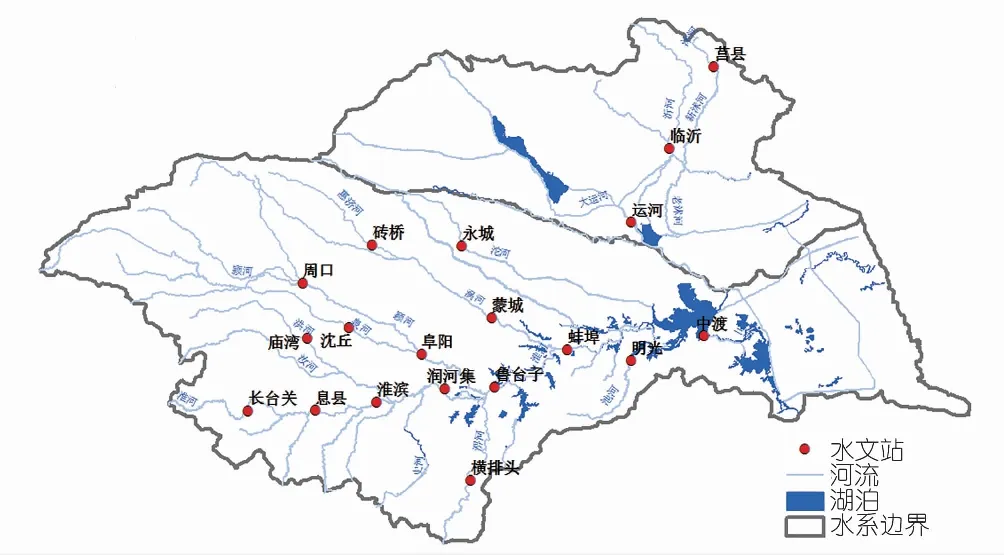
图3 淮河流域主要水文站点分布示意Fig.3 Distribution of the main hydrological stations in Huaihe River Basin

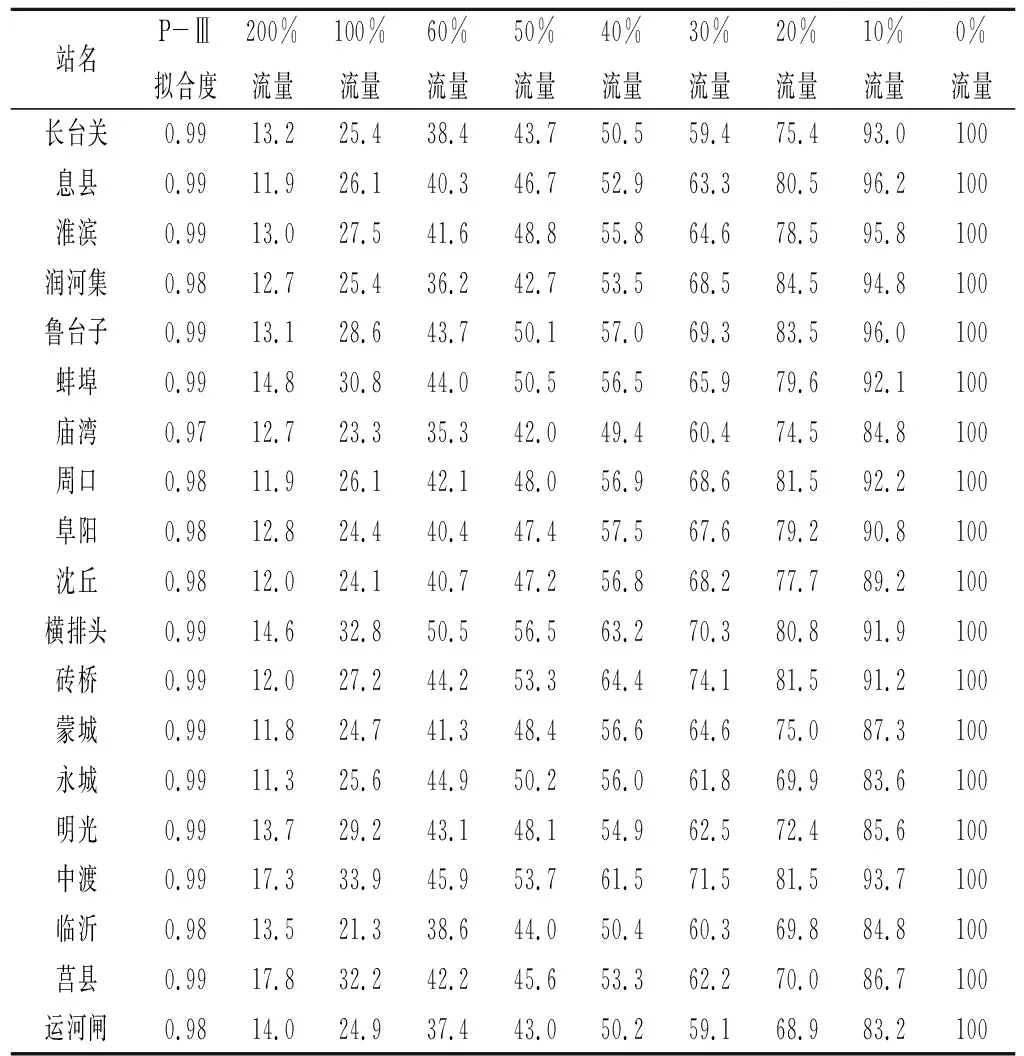
Tab.2 The hydrological guarantee rates corresponding to the flow recommended by Tennant method in the main tributaries of the Huaihe River Basin %

2.2 不同栖息状态水文保证率计算

基于淮河流域主要干支流上19个水文站点1956～2014年实测月均流量资料，利用P-Ⅲ曲线推求Tennant法不同栖息状态下推荐流量水文保证率，计算结果如表2所示。从表2可以看出，各站点流量分布均符合P-Ⅲ曲线，拟合度均在0.95以上，且多年平均流量比值保证率与比值呈幂指数递减；不同站点同一栖息状态下的流量比转换后保证率存在差异，其中20%状态下的差异最大为15.59%，200%状态下的差异最小为6.51%。

2.3 河流不同栖息状态下保证率确定

本文利用方差与四分位图，进一步分析不同推荐流量百分比下各站点的水文保证率，结果如图4所示。

由图4可知，虽然不同推荐流量百分比下水文保证率四分位数区间存在一定差异，但方差均在5%之内，且流量比值越大方差越小，说明流域内各水文断面转换后的保证率分布相对集中。因此，本文选择淮河流域19个流量站点转换后的保证率均值，作为整个流域不同栖息状态对应的保证率，具体见表3。

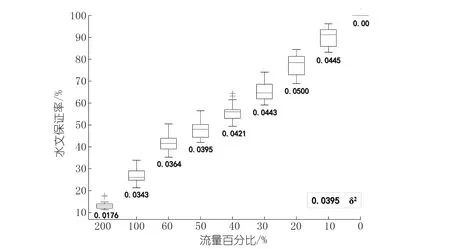
图4 淮河流域不同流量百分比下水文保证率箱型图Fig.4 Hydrological guarantee rate box diagram at different flow rates in Huaihe River Basin

流量及相应栖息地的定性描述一般用水期(10月～翌年3月)推荐流量(多年平均流量百分比)/%水文保证率/%鱼类产卵育幼期(4～9月)推荐流量(多年平均流量百分比)/%水文保证率/%最大20012.820012.8最佳范围60～10027.0～41.660～10027.0～41.6极好4054.76041.6非常好3065.45047.9好2077.14054.7中1090.23065.4差1090.21090.2极差0～1090.2～100.00～1090.2～100.0

2.4 应用实例

淮河入海水道为束洪型河流，西起洪泽湖东侧二河闸，东至扁担港入黄海，总长162.3 km。入海水道除二河新闸、东沙港闸、海口闸为水文站外，其余站点均为水位站点。但是，由于二河新闸仅在行洪时开启，因此各站缺少流量观测资料。同时，由于入海水道修建于2003年，水文与水位站点大部分建立于2009年。其中，淮阜控制调度闸和东沙港闸水位站点资料较完整。本文选择淮阜控制调度闸和东沙港闸站点水位资料，应用基于Tennant法改进的生态水位计算方法开展淮河入海水道生态需水研究。

淮阜控制调度闸日均水位时间序列为2006年1月1日～2015年12月31日，东沙港闸日均水位时间序列为2004年1月1日～2015年12月31日。鉴于2007年7月入海水道进行了行洪，统计中未采用2007年7月数据。淮河入海水道主要水系及水文站点分布情况如图5所示。

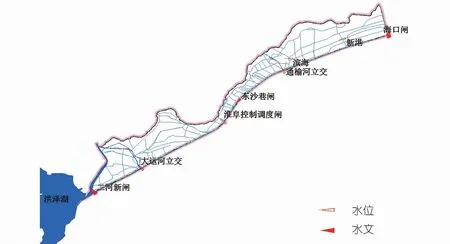
图5 淮河入海水道水系及水文站点分布情况Fig.5 Distribution of water systems and hydrological stations in sea-entering channel of Huaihe River

根据基于Tennant法推求的水文保证率，不同栖息状态下淮河入海水道淮阜控制调度闸与东沙港闸的生态水位计算结果如表4所示。

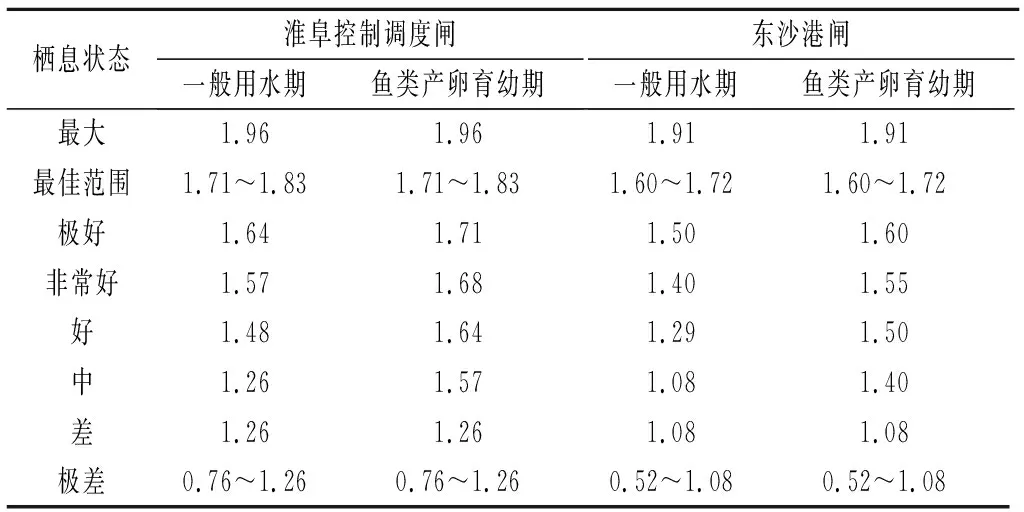
表4 淮阜控制调度闸与东沙港闸不同栖息状态下生态水位Tab.4 The ecological water levels of Huaifu control floodgate and Dongshagang floodgate m

由表4可知，不同栖息状态下淮阜控制调度闸(上游)生态水位均高于东沙港闸(下游)，鱼类产卵育幼期生态水位高于或等于一般用水期，符合经验事实。同时，淮阜控制调度闸生态水位最佳范围为1.71～1.83 m、差为1.26 m；东沙港闸生态水位最佳范围为1.60～1.72 m、差为1.08 m。为保证河道生态需求，建议入海水道淮阜控制调度闸和东沙港闸水位应分别尽量保持在1.26～1.83，1.08～1.72 m之间。

3 结 语

(1) 本文基于Tennant法，提出了一种适用于流量资料缺乏型河流的生态需水计算方法。该方法将Tennant法中推荐流量占多年平均流量的百分比与水位保证率进行关联，计算不同保证率下水位作为不同栖息状态的生态水位，并进行空间差异性检验，实现了流量资料缺乏型河流的生态需水计算。

(2) 以淮河流域为例，基于流域内19个水文站点长序列流量资料，利用P-Ⅲ曲线推求Tennant法推荐流量阈值相应的水文保证率；进行流域内代表性站点不同栖息状态所对应的水文保证率空间差异性检验，选取所有断面保证率的均值作为淮河流域河流系统不同栖息状态水位保证率。结果为栖息状态为差与最佳的水文保证率分别为90.2%，27.0%～41.6%。

(3) 基于Tennant法改进的生态水位计算方法，束洪型河道淮河入海水道淮阜控制调度闸和东沙港闸水位应保持在1.26～1.83，1.08～1.72 m之间。该结果对束洪型河道生态需水保障具有重要意义。