基于改进透视变换的结构光图像校正∗
2019-06-01王颖李锋
王颖 李锋
(江苏科技大学电子信息学院 镇江 212003)
1 引言
在光栅投影三维结构光成像系统中,由于投影仪投影角度、相机拍摄角度等因素的影响,使得相机获取的结构光图像发生不同程度的透视畸变[1]。但在结构光后续处理中,如结构光相位误差补偿等,通常需要结构光图像的无畸变正视图图像,因此在进行后续处理之前需要对畸变结构光图像进行校正[2]。
常用的图像校正方法主要有角度检测法[3]和透视变换法[4]。角度检测校正方法依据检测的图像中的直线角度,进行旋转校正,忽视图像透视畸变,存在一定局限性;透视变换校正方法从投影仪和相机的成像原理出发,对图像透视畸变进行校正,效果较好,但透视变换校正方法首先需要精确获取控制点坐标,常用的基于Hough变换检测方法[5],精度不高且稳定性差。
文章提出一种改进的透视变换方法,用于畸变结构光图像的自校正。采用高斯梯度方向亚像素拟合曲线的方法更加精确地检测到投影结构光图像边缘,使透视变换矩阵更加准确。
2 理论基础
2.1 透视投影
透视投影也称作投影映射,是将图像投影到一个新的视平面。利用透视中心、像点、目标点三点共线的条件,按透视旋转定律使透视面绕透视轴旋转某一角度,破坏原有投影光线束,仍保持透视面上投影几何图形不变的变换[6]。
由于观察视角的不同,可以看到一个物体的一个或多个侧面,按照透视中空间坐标系划分,可以分为单点透视投影、双点透视投影和三点透视投影[7]。文中讨论的是单点透视投影,即投影仪投射图像到投射面,投射面的图像发生透视畸变,利用透视变换的相关算法对其进行矫正。
2.2 二维图像的透视变换
以点S为视点,由于视线与矩形ABCD所在的平面存在一定的夹角,使得投影面上的图像发生透视畸变,形成新的四边形,如图1所示。
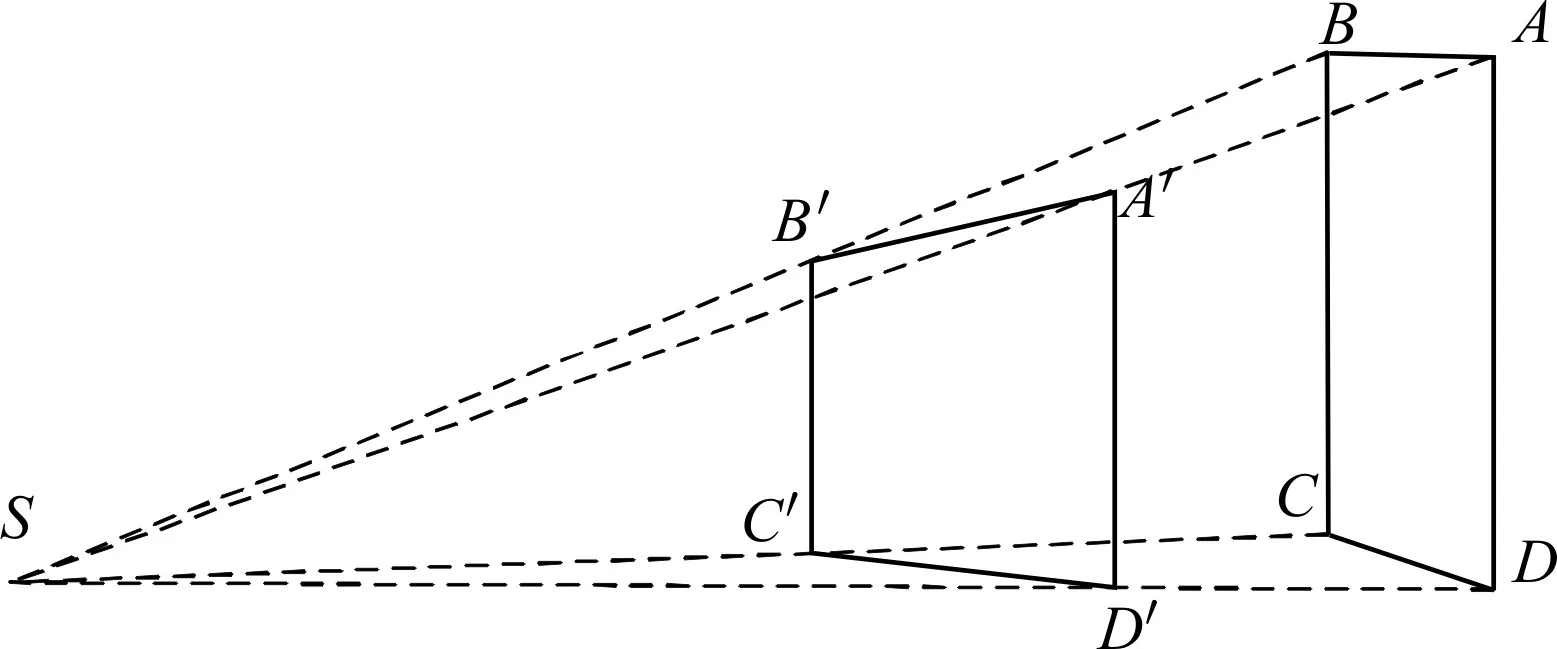
图1 透视变换
以图中的四个角点为例,经过透视变换后,A点对应 A′点,B点对应 B′点,C点对应C′点,D点对应D′点,原四边形的形状发生改变。透视投影是矩形ABCD平面上的每一个点在视角的作用下投影到 A′B′C′D′平面的过程。若矩形 ABCD 为无畸变正视图,则透视变换是畸变图形 A′B′C′D′上的每一个像素点对应到正视图上对应的像素点的过程[8]。而实现透视畸变的矫正,就是要找到A′B′C′D′平面上的点与正视图上的点的一一对应关系。
通用的变换公式为
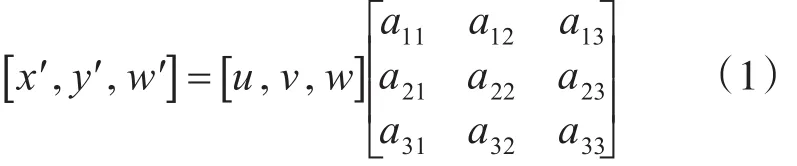
式中,u,v是原始图像的某点坐标,经透视变换后得到的对应图像坐标为 x,y,其中 x=x′/w′,透视变换矩阵,可拆分成四部分,其中,表示线性变换用于平移产生透视变换。重新整理公式可以得到:
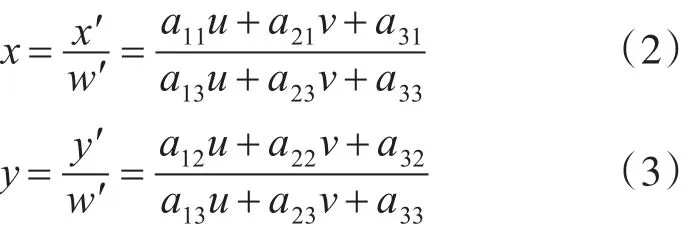
其中,(x,y)是正视图的像素坐标,(u,v)是畸变图像的像素坐标,a11,a12,a13,a21,a22,a23,a31,a32,a33是透视变换的参数。
2.3 透视变换坐标点的选择
由式(2)、(3)可以推出,只要得到四对畸变图像与正视图像相对应的坐标对就可以解出透视变换参数,从而求得透视变换矩阵。四对坐标点的选取对实现高精度透视畸变校正有很大的影响。一般选取畸变图像的四个角点的坐标,角点较于其他点更容易获取且分布均匀。然后需要确定角点对应在正视图中的位置坐标,对应不同的正视图角点的坐标,其校正结果也不同。通常的算法是将图像实际的尺寸转换为相应的坐标值,但这样会导致校正之后的图像边缘不连续,出现断层现象,需使用灰度插值法来保证图像的连续性和平滑性[9]。
在结构光图像的实际应用中,按照同样的准则选取图像中结构光投影区域四个边角点,作为透视变换控制点和确定相应的正视图控制点。希望校正后的图像还能保持结构光的正弦特性,周期要与系统拍摄的正视图的结构光周期一致,也将以此来判断校正的效果。
2.4 角点坐标的确定
由透视变换理论分析可知,角点坐标是影响透视变换的一个主要因素,对于一个结构光图像而言,需要对投影图像的边缘曲线进行解析,从而获得四条边缘曲线的交点,即为所求的角点。
文章采用一种高精度亚像素边缘检测算法,目前研究的亚像素级边缘曲线检测算法,可以归纳为3种类型:矩方法[10]、插值法[11]和拟合法[12]。矩方法对图像噪声敏感,如果考虑模糊后的边缘模型,就会增加模型参数,使得解析解的确定变得十分困难。插值法的特点同基于矩的方法类似,计算过程简单,但是容易受噪声的影响。
插值法和拟合法求边缘,易受噪声影响。若考虑在求边缘前进行图像的滤波去噪处理,容易造成部分边缘信息的丢失[13~14]。针对这种情况,文章采用一种新的拟合算法用于边缘曲线的检测和提取。首先在边缘附近选取一系列的点,获取这些点的灰度值,进而求得灰度梯度值,然后利用高斯曲线对这些点的梯度值进行拟合,最后通过拟合曲线求得高斯曲线的对称轴位置即为亚像素位置。该方法去掉离群点的干扰,故对噪声不敏感。
2.5 一种高精度的边缘拟合算法
首先在图像边缘选取某一领域U,设H是在该领域内的矩阵,表示在领域内(i,j)点的灰度值,求得灰度矩阵H。
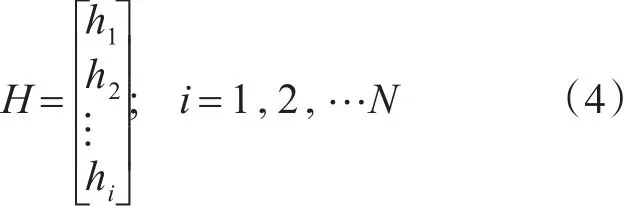
若灰度分布函数为y=f(x),则梯度函数为t=f(x)′。再根据梯度值进行高斯拟合。由梯度值得到的是离散的点,必须将这些离散的点拟合成一条连续的曲线,高斯分布的中心为该梯度方向上的灰度变换最大的地方,也就是边缘,以此来确定亚像素边缘坐标[15]。
高斯曲线的表达式为

式中u为高斯分布均值,σ为标准差,对式(4)两边取对数得
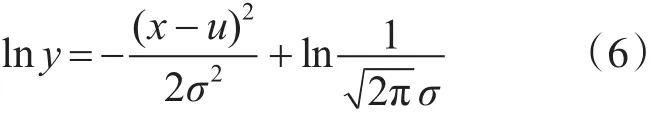
变化后得到的式(5)为典型的二次曲线,计算得到简化。
用于拟合边缘的曲线方程为y=ax2+bx+c,由最小二乘法原理求取参数a,b,c,误差平方和用字母S表示:

将S分别对a,b,c求偏微分,并分别令其偏微分为零,得:
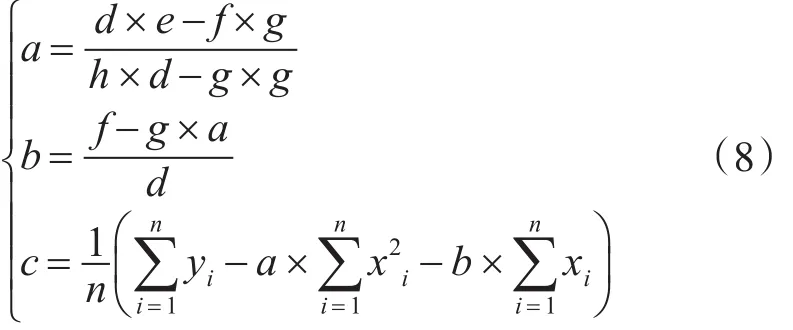
其中:

进而求得u和σ:

u值即为边缘曲线亚像素值。
然后求得拟合的四条边缘曲线的交点作为结构光畸变图像的角点进行透视校正。
3 实验分析
实验系统结构如图2所示,将正弦性结构光经投影仪投射到投射面,投影仪与投射面存在一定角度,相机拍摄得到的结构光图像如图3(a)所示。
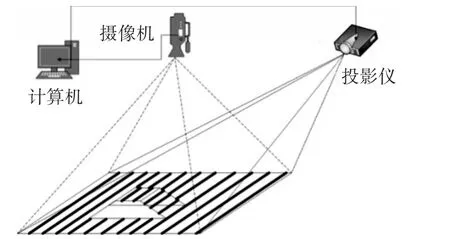
图2 试验系统
对图3(a)发生畸变的结构光图像用文中所述方法进行校正,如图3(b)所示。

图3 (a)畸变结构光图像

图3 (b)校正后的结构光正视图
再调整投影仪的位置,使投影仪、相机和投射面平行,拍摄得到正视图,如图4所示。
将图4的结构光正视图图像取行像素灰度,如图5(a)所示;取图3(b)经过透射变换校正后的结构光图像的行像素灰度,如图5(b)所示。

图4 拍摄得到的正视图
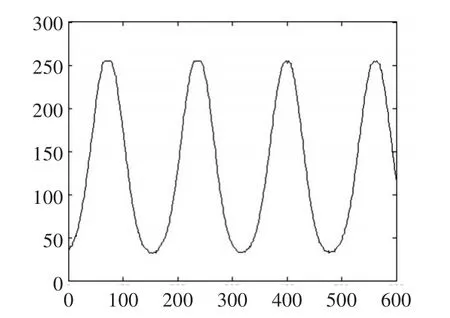
图5 (a)拍摄的正视图的行像素灰度
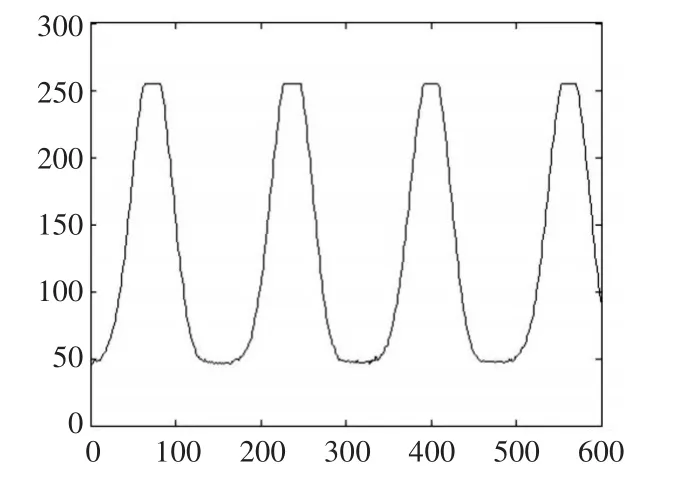
图5 (b)校正后的正视图的行像素灰度
通过对比图5(a)和图5(b)可知,将畸变图校正后得到的正视图仍具有正弦性,且频率与正常情况下拍摄得到的正视图相同。
4 结语
为实现图像的透视校正,通常要对图像的角点进行精准定位,也就是对图像边缘的精确测量。文章提出一种新的边缘检测算法——梯度方向亚像素边缘拟合,先在边缘附近取点,求这些点的梯度,再用高斯模型对其梯度进行拟合得到亚像素位置,求取直线边缘,得到角点。
通过对结构光图像的畸变校正,可以看出该算法速度快、效率高、实用性强,维持了图像原有的特性,有较好的应用前景。
