基于小波变换灰度与彩色图像融合算法研究

姚洪涛，侯怀侠，白会东

（长春理工大学计算机科学与技术学院，长春 130000）

灰度CMOS 图像传感器由于去掉彩色滤光片，进光量是彩色CMOS 图像传感器的三倍，故将灰度CMOS 图像传感器和彩色CMOS 图像传感器进行融合可以增加融合系统的夜视能力和动态范围。因此提出一种灰度与彩色图像融合算法，该算法是基于小波变换与HSI 颜色空间转换的融合方式，同时提出一种基于梯度因子、灰度标准差、均亮度值的动态融合权值确定方式，并运用MATLAB 等图像处理工具进行仿真验证。

图像融合；小波变换；HSI 颜色空间

0 引言

CMOS 图像传感器发展迅猛，在数码相机、手机拍摄、安防监控等数字成像系统方面应用广泛，由于CMOS 图像传感器作为一种典型的固定成像传感器，具有成像性能良好，制作成本低等多个优良特点，未来发展前景和市场巨大。针对安防监控与倒车影像系统中单个镜头成像信息的缺失，单彩色CMOS 图像传感器成像亮度不足，在光线较差的环境中成像效果较差。单灰度CMOS 图像传感器成像缺乏色彩信息，但由于灰度图像传感器去掉了彩色滤光片，进入光量是彩色图像传感器的三倍[1]。

结合两者的优劣特点为此本实验室设计灰度与彩色双CMOS 融合成像算法，获得更加明亮清晰的图像信息，提高图像动态范围。同时根据人眼成像特点，人眼中分为两种细胞，杆状细胞只能感受亮度信息，锥状细胞可以感受亮度和色彩[2]。进行灰度和彩色的图像融合可以实现更加接近人眼的视觉效果。

所以本文提出了一种基于小波变换和颜色空间转换的灰度与彩色图像融合算法，并且根据灰度标准差、梯度因子、灰度均值确定动态融合权值。同时提出了饱和度均匀化的方法进行HSI 颜色空间中S 通道的融合。

1 理论基础

1.1 小波分解与融合

基于小波变换的图像融合就是把源图像进行小波变换，如图1 把它分解到不同的频段内，然后在不同的频段内选用不同的融合规则分别进行融合。

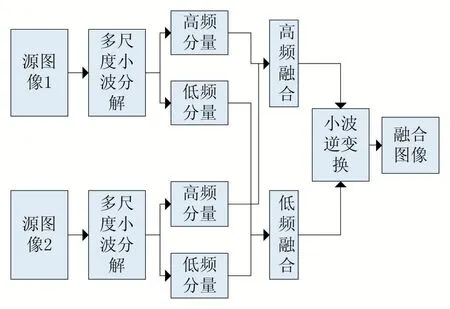
图1 小波分解与融合

根据查阅资料可知，不同的小波系所具有的性质不同，表1 为各个小波系性质对比[3]。

表1 不同小波系性质

同时不同分解层次也有不同的效果，分解层次过少，无法很好地分解出低频轮廓部分，分解层次过多则会造成低频轮廓部分丢失过多。

本文采用sym4 小波、五层分解、多层二维离散小波分解函数wavedec2（）进行分解和waverec2（）重构。sym4 小波属于Symlet 小波系是近似对称的一类紧支正交小波函数，它具有dbN 小波系的一切良好特性，而在对称性方面的改进，又使得该小波系在信号处理方面避免了不必要的失真。

在MATLAB 中wavedec2 是多层二维离散小波分解函数。[C,S]= wavedec2（X,N,'sym4'）为分解函数形式，X=waverec2（C,S,Lo_D,Hi_D）为重构函数形式。[C,S]=wavedec2（X,N,'sym4'）该函数值利用母小波函数sym4 对于图像矩阵X 的第N 层进行二维离散小波分解，N 为正整数；返回结果为分解系数矩阵C 和分解系数长度适量矩阵S。X=waverec2（C,S,sym4）是利用指定的sym4 实现多层图像矩阵的二维离散小波重构[4]。

1.2 颜色空间转换

此处的RGB 转HSI 的公式采用算法几何推导法，HSI 转RGB 是逆运算。首先是RGB 转HIS。

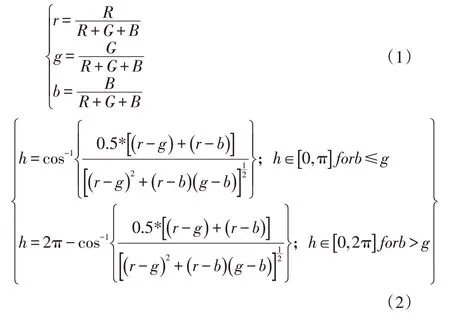
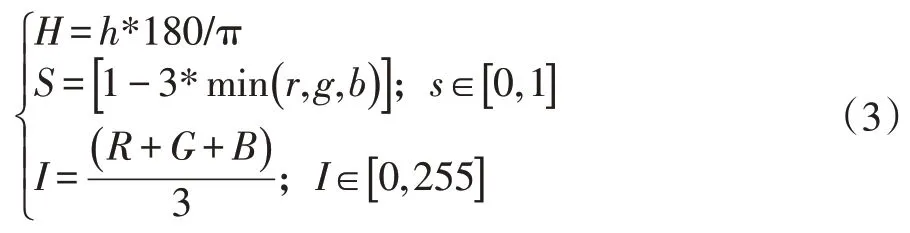
然后是HSI 转RGB：

则可以求得R、G、B 完成从HSI 颜色空间到RGB颜色空间的转换[3]。

2 算法描述

图1 是灰度与彩色图像融合算法的结构框图，其具体算法步骤为：先对两源图像进行颜色空间转换，由RGB 颜色空间结构转到HSI 颜色空间结构，然后针对所得两个I 通道图像分别进行小波分解和融合，期间进行样本训练确定两I 通道融合权值，进行四样本参考快速融合。同时S 通道进行饱和度均匀化处理，对H 通道则进行简单叠加，最后对融合后的HSI 三通道分量进行颜色空间反变换得到RGB 颜色空间结构输出图像。

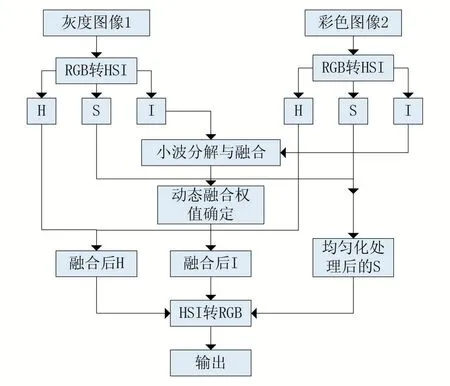
图2 灰度与彩色图像融合算法

2.1 融合权值确定

不同融合方式中融合权值的选择多种多样，如文献[1]中高频分量采用均值法，低频分量采用最大值法。文献[5]中高频分量融合系数采用的是两图像在单个像素为中心的局部区域最大均方差值的小波系数，低频分量采用绝对值最大法。在单帧静态图像融合中这些方法都是有一定可取性，但是在复杂多变的动态环境下，固定的融合系数显然是不适应的，动态融合系数的确立是支持动态融合的关键。而且当每一次单帧融合都重新确立融合权值，速度显然是达不到动态视觉的要求。

因此主要针对动态融合中的环境多变性和动态视觉对融合速度的要求，提出一种基于灰度标准差和梯度因子以及均亮度的融合权值确定方法。

2.2 关于确定动态融合权值的研究

首先在[C,S]=wavedec2（X,N,'sym4'）分解函数中，C为各层分解系数，S 为各层分解系数长度即大小。C 的存储结构为：

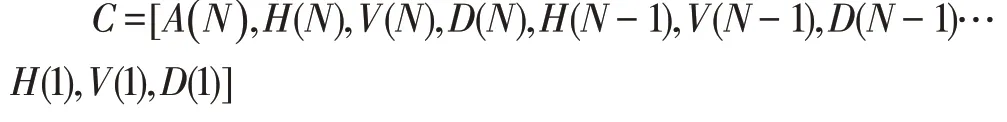
其中A（N）代表第N 层的低频分量系数，H（N）代表第N 层的水平高频分量系数，V（N）代表第N 层的垂直高频分量系数，V（N）代表第N 层的对角高频分量系数。S 的结构是储存各层分解系数长度的，即第一行是A（N）的长度（其实是A（N）的原矩阵的行数和列数，第二行是H（N）|V（N）|D（N）|的大小，第三行是H（N-1）|V（N-1）|D（N-1）的大小，倒数第二行是H（1）|V（1）|D（1）的大小，最后一行是图像X 的大小。所以融合中的两个图像S 的大小相同而C 的取值不同[4]。

固定的高频和低频融合规则显然是无法适应多变的环境。故而，各个尺度上的每个频率子带都有其独立了融合规则则可以实现最佳的融合效果。故而本文从梯度因子，灰度标准差两个标准去确立各个频率子带的融合规则。由于C 的结构是一个1*N 的矩阵结构。故而设立一个1*N 的结构矩阵作为权值矩阵P 和Q 然后把权值矩阵P 和Q 转化为对角矩阵diag（P）和diag（Q），所以融合后的C=C1*diag(P)+C2*diag(Q) 。如何确定权值矩阵，需要进行以融合后的图像梯度因子和灰度标准差为参考基准进行衡量。本文样本训练实验中采用的为364*500 大小的图片，在5 层sym4 小波函数分解下C 为1*193062，每个系数权值p 和q 可取0。1 到2 之间20 个取值。采用一种简化的权值确定方式。利用MATLAB 构建关于全局灰度标准差k与p、q 的函数关系k=f(p,q)。不同的融合权值可以得到不同的融合结果，融合权值越大灰度标准差越大，但是增加到一定程度开始下降。下图分别为全局灰度标准差与权值p、q 函数关系图，全局梯度因子与权值p、q函数关系图。如图越接近黄色数值越大，越接近蓝色数值越小。

图3 灰度标准差与权值p、q函数关系图

图4 全局梯度因子与权值p、q函数关系图

结合灰度梯度因子，以及融合后的灰度均值可以得出良好的融合权值。图5 为图像均亮度值与权值p、q 之间的函数关系图。

图5 图像均亮度值与权值p、q之间的函数关系图

根据实验数据分析以及图像观察多组图像融合可得当梯度因子和灰度标准差达到全部遍历值最大值的70-80%时以及灰度均值在0.5 附近时图像成像效果最佳。

2.3 S通道融合

I 颜色通道通过以上的权值遍历策略和四样本参考快速融合可以得到清晰度很好的图像，但是S 空间中需要进行调整，如图6 所示标准彩色图像S 通道图像明显优与待融合的彩色图像S 通道信息。

图6 S通道图像对比

标准彩色图像HSI 三通道分解后S 图像与待融合彩色图像HSI 三通道分解后S 图像可以看出右侧部分存在一定差异。由于灰度图像没有H 和S 通道分量。而彩色图像的S 分量由于焦点变化与标准彩色图像的S 通道分量存在一定差异，若想实现不同焦点的灰度与彩色图像融合得到更好的融合后彩色图像，需要对彩色图像S 通道图像进行处理，由于S 保存的是彩色图像颜色的饱和度同时灰度图像不存在颜色S 通道分量。

饱和度是彩色图像中颜色的鲜艳程度，饱和度越高图像颜色越加鲜艳，饱和度越低图像鲜艳程度越低，显着更加的昏暗。

图7 饱和度

根据实际拍摄中图像亮度对饱和度的影响，实际拍摄中环境光线越好，则可以获取到的颜色种类信息越加丰富。故而本文提出一种基于灰度图像亮度均值的颜色饱和度调整方法，灰度图像I 的取值为0 到256，又由于可见光为7 种颜色赤橙黄绿青蓝紫频率谱分布，故将亮度大于128 的点进行饱和度降低处理，亮度小于128 的部分进行饱和度增加处理。

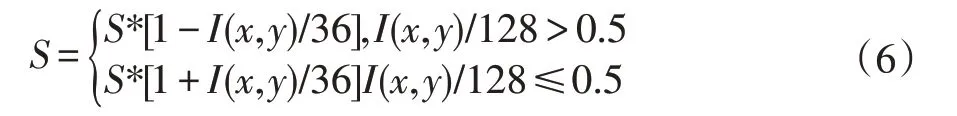
经过饱和度增强处理后图像细节明显增强，但是出现白色成分的失真，如图8 所示。

图8 图像经饱和度均匀化处理前后对比

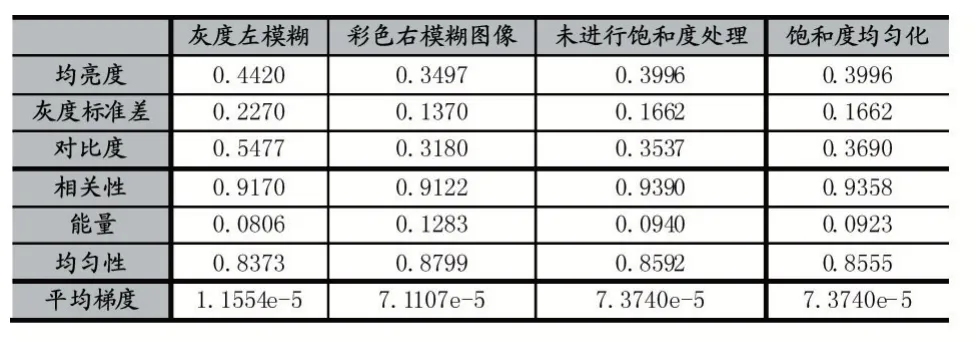
表2 饱和度均匀化前后对比

通过上表数据可以看出，经过饱和度均匀化之后的图像在对比度方面得到明显提高。图像清晰度和细节丰富度上也得到了明显提升。

3 结语

通过后的实验结果反应出算法的可行性，在动态融合权值确定，不同组的融合图像所得到的灰度标准差与权值p 和q 的函数关系1、梯度因子与权值p 和q的函数关系2、图像均亮度值与权值p 和q 之间的函数关系各不相同。通过取均亮度值为0.5 匹配另两个函数关系中的全部遍历最大值的70-80%，从而确定最终的融合权值p 和q。针对图像色彩饱和度S 通道融合，采用饱和度均值化的方法大大提高了图像细节信息和清晰度。但是对白色成分略有丢失。

总之，针对单一CMOS 图像传感器在实际暗光条件下性能和动态范围的缺失，本文着力研究了灰度与彩色图像的融合算法，使得成像动态范围大大增加，实际应用更加灵活，对环境光线变化的适应能力明显增强，通过利用灰度与彩色图像的融合使得双CMOS 图像传感器成像系统，在复杂多变的环境中始终保持较为良好的成像结果。

目前为止，图像融合技术应用领域极为广泛，融合算法的适应性和智能化程度越来越高，但至今仍旧缺乏智能化广泛适应性图像融合算法。本文虽实现灰度与彩色图像较好的多动态范围融合，但在智能化融合模式学习以及动态融合调整和硬件实现难度降低方面仍然需要做出改进和进一步深入研究。