运输车辆机器人存取车路径优化算法研究

陈宁，梁欢欢，孔祥希，胡立渝，韩吉

（南京农业大学工学院，南京 210000）

针对智能停车库中的运输车辆机器人AGV，首先根据停车场结构示意图，对某一时刻停车场实际路网进行抽象，将要求的路径优化问题转化为最短路径问题。与实际问题相结合确定停车场AGV 路径优化的算法为Dijkstra 算法，最后通过MATLAB 软件编程算法并进行求解，算出每个空闲车位相对应的最短的存取车路径及距离总和，提高AGV存取车效率，节省时间。结果证明Dijkstra 算法在AGV 存取车路径优化中的可行性和实用性。

智能停车库；运输车辆机器人；最短路径；Dijkstra 算法

0 引言

随着当今社会经济的快速发展，全国汽车的保有量也在不断上升。汽车的持有量急剧增长与停车位稀缺的矛盾亟需解决[1]。最直接的解决方法就是建立停车场，但相对应的停车场内部的车位更加拥堵，使得停车变成了候车过程久、停车过程乱、取车过程忙的现象。为了解决这种现象，建立一种高性能的智能化停车场成为一种必然趋势。当前市面上应运而生了很多种类的智能停车库，例如智能立体停车库、半自动立体停车库以及基于运输车辆机器人的智能化停车库等。基于AGV 的智能停车库与别的类型停车库相比，具有占地面积小、车位利用率高、性价比及可靠性高等特点[2]。在实际中调查中我们发现运输车辆机器人AGV 在存取车路径的选择上还存在问题，大部分是依靠人工在后台控制，并不能智能选择最优路径使得存取车路径最短而减少工作耗时。解决运输车辆机器人存取车路径优化算法问题，是发展AGV 智能车库的基础。针对路径优化问题，随着算法的不断发展，Dijkstra 算法、A*算法、遗传算法以及蚁群算法等也被广泛用于解决各领域路径规划问题[3]。

在分析了智能停车场的系统组成和运输车辆机器人的工作原理后，本文着重研究运输机器人的路径优化问题，该问题的优化使得运输机器人在较短的时间内走最短的存取双向路线，即AGV 将待取车从取车车位运输到出入口，再将待存车从出入口运输到最近空车位。此优化方法将为我们节省更多的存取车时间，提高智能停车场的运行效率，减少运输车辆机器人的耗能。针对智能停车库中AGV 存取车路径优化问题，建立模型车车场模型，本文研究了几种算法后进行比较，最后选取较为适合的算法作为本文的主要研究算法，编写程序进行求解，从而得出优化后的该选择的路径。

1 AGV在智能停车场的应用

本文所涉及的AGV 智能停车场系统主要包括机械系统、管理系统、监控系统及其他系统等如图1所示。

智能停车场中，在正常的电磁导引系统环境和车载通讯系统环境下，AGV 处于待机状态。当有车辆要求停车时，地面管理调度系统通过机载通讯系统向运输车辆机器人下达作业指令，通过上位机系统比对停车场内车位、车辆停放信息，然后智能停车场管理系统的主控计算机通过算法可迅速得到最佳车位并进行路径的规划，车载计算器接受其他系统获取到的环境信息和路径信息以及上位机系统控制信号所规划的路径。在接受到运输任务后，AGV 开始执行任务，驱动系统驱动AGV 运输车辆实现AGV 的沿着所规划的路径进行运行，将车运送到所指定的位置。

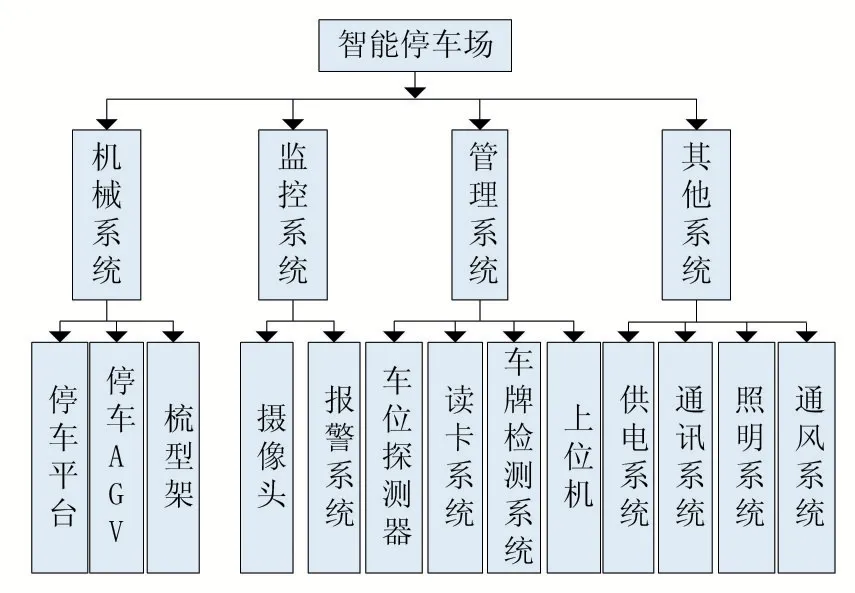
图1 智能停车场系统结构图

运输车辆机器人结构图如图2 所示。

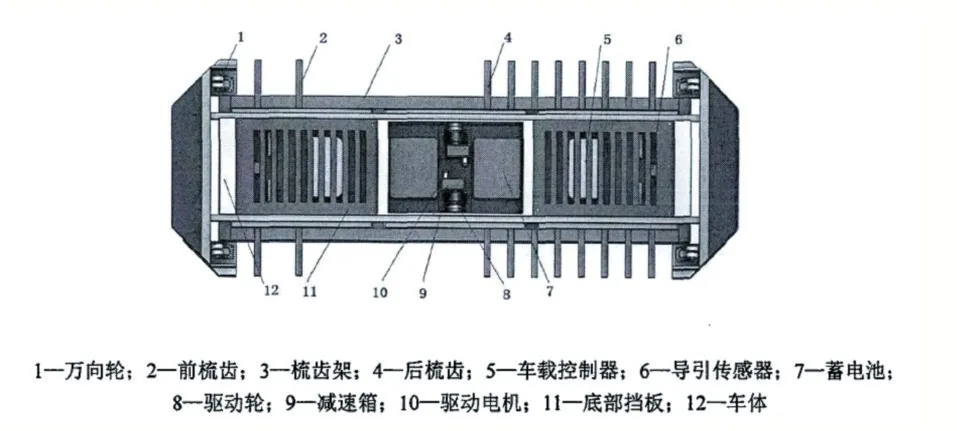
图2 停车AGV结构图

2 问题描述与建模

2.1 问题描述

智能停车场系统通过检测装置来获取车库中停车位的占用情况，根据AGV 当前状态，快速地为AGV 找到一个最佳车位并规划出从当前车位到该车位的最优路径，保证AGV 在较短时间内完成车辆存取车任务，以便提高运输车辆机器人的运输效率。

本文假定：①停车场的出口与入口在同一位置；②运输车辆机器人完成存车命令后将在该车位处待机，等待下一命令；③行车道宽度满足AGV 最大转弯半径，道路宽度需保证单个AGV 正常行驶；④忽略AGV 实际大小，把AGV 和停车位视为质点。

2.2 停车场抽象结构模型

假设停车位宽为3 米，长为6 米，行车道宽度为6米，这里将智能停车场中位置信息，例如空车位、交叉口、出入口等抽象为节点[4]。智能停车场入（出）口为S（1），交叉路口为2-10，当前空闲车位为P1-P10，表示可以用来存放车辆，其余的车位均已被占用。编号标记如图3 所示。

图3 停车场结构示意图

以O 点为原点建立坐标系，把每个车位看作一个质点，每个质点的坐标为该车位中心点的坐标[5]，每个交叉路口点的坐标为该交叉路口中心点的坐标，图中的入口、出口、有效停车位以及交叉路口的坐标就可以被确定如表1 所示。下一步的研究工作将以此模型为基础，研究运输车辆机器人最优路径规划算法问题。

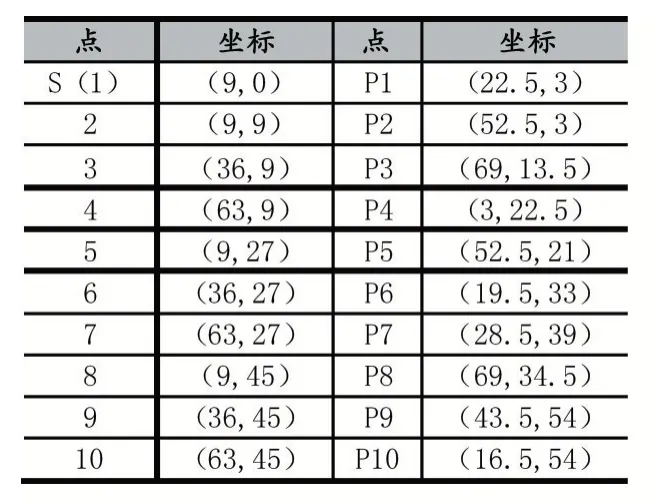
表1 坐标点

2.3 最佳车位模型

根据上述可知，本文所研究的寻找最优路径的问题就是运输车辆机器人把待取车运送到出入口后，再将待存车运进停车场时，对余下的空车位按照设定的计算规则进行分析处理，得到一个最合适的停车位，并找到该车位的最短路径。若某个空闲车位为Pi（i=1，2，...，n），运输车辆机器人把某一固定车位的待取车运送到出入口的最短路径为path（P，s），运输机器人把待存车送到某空闲车位对应的入场过程的最短路径为path（s，Pi）。

则运输车辆机器人存取车过程对应的整个最短路径长度为：

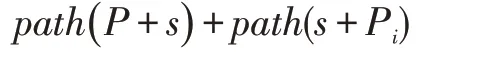
则最佳车位所对应的最短路径的长度可表示为：

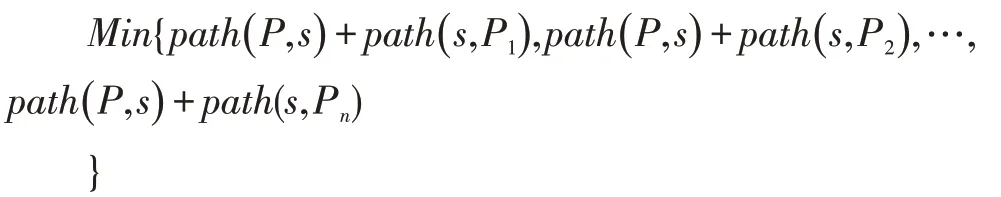
2.4 路网的构建

按照图论[6，7]的构图方法，某一时刻停车场路网是静态的，结合上述停车场的结构示意图和停车场内空闲车位的信息，可以把图示停车场结构示意图的构建成为一个带权的有向图，AGV 在停车场静态路网里的存取车路径优化问题就可转换成求解带权图中任意指定的节点间到其他点的最短路径问题。

停车场内路网有向图可以用如下来表示：

图中停车场内的出入口（S）、行车道交叉路口、空闲车位可以构成一个顶点集V，每一条路径对应一条弧E，连接两顶点之间的路径长度看作为弧的权值，用W 表示，如果两个顶点之间没有连通的道路，那么权值可以用∞表示，所转化成为的赋权图如图4 所示。

3 Dijkstra算法

有很多算法都可以用来求出在某个赋权有向图中的任意两个结点之间的最短路径，如蚁群算法[8]、遗传算法、Dijkstra[9]算法等。由于本文研究的是应用在停车场中最短路径问题，所以赋权图中的各条边的权值均为非负，相对于其他算法而言，Dijkstra 算法更适用于此场景下最短路径的问题研究。Dijkstra 算法由荷兰E.W.Dijkstra 提出的一个典型的单源最短路径算法，用于计算赋权图上一个节点到其他所有节点的最短路径。算法从起始点开逐个搜索下一邻接点，直到搜索到终点为止。Dijkstra 是很具有代表性、经典的最短路径算法，并且在实际中应用广泛。1969年Zhan 等使用实际交通网络测试了15 种不同的最短路径算法，结果表明，Dijkstra 算法计算某一点到其他点的最短路径最快捷[10]。

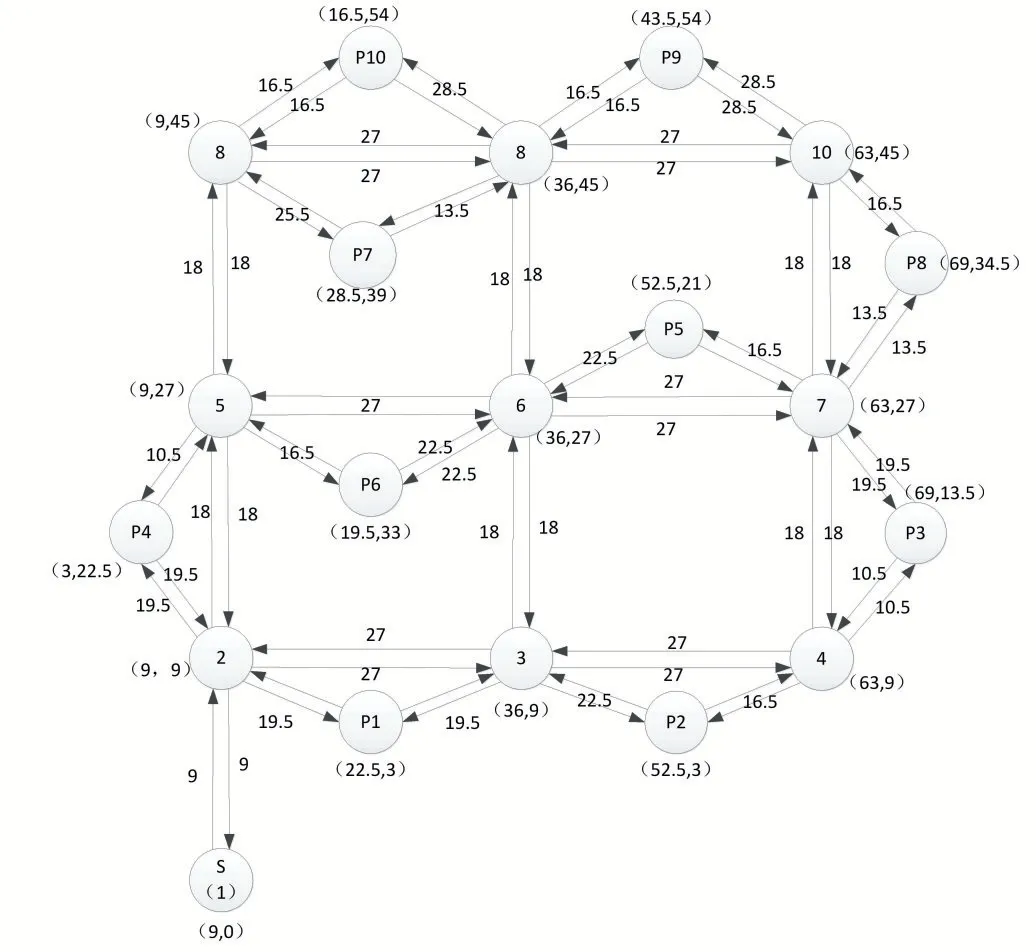
图4 带权有向图

Dijkstra 算法思想为：设G=（V，E，W）是一个赋权有向图，把有向图中顶点集合V 分为两组，第一组我们就称它为A 集合，代表已经求出源点到该点的最短路的点的集合，开始时A 集合中只包含源点v0。另一个我们称为B 集合，代表未求出源点到该点的最短路径的点的集合。找出点集B 中最短路径的顶点并将其加入到点集A 中，接着更新B 中的顶点及对应的最短路径按，不断进行以下操作，按照最短路径长度递增的顺序逐渐把B 集合中的点加入到A 集合中，直到点集B中的点全部转移到点集A 中。

算法步骤如下：

步骤1：初始化行驶的最短路径集合A，最开始时集合A 只包含始点即出入口设为v0，除v0之外的其他顶点都在B 集合中。即A={v0}，B={其他顶点}；

步骤2：从集合B 中选取一个距离v0最小的顶点再将vk加入到集合A 中（该选定的距离就是v0到vk的最短路径长度）。

步骤3：然后对B 中点到源点的距离进行一次更新，就是以vk为中间节点，修改A 中各顶点到源点的距离。如果经过vk，可以使v0到某个未访问过的顶点距离变小，则修正该最小距离。

步骤4：重复步骤2 和3 直到所有顶点都包含在集合A 中。

4 MATLAB编程求解

根据上述算法步骤进行编程，在MATLAB 环境下实现Dijkstra 算法，验证算法的合理性和正确性。以图所示的停车场为实验场景，假设H15 号（H 区从左往右第15 个车位）有一辆车需要取出，向AGV 运输管理系统发送任务请求，运输车辆机器人把H15 号的车运送到出入口，再将出入口的待存车运送到某一空车位。管理系统在收到任务后进行路径的规划，并将规划的路径下发给对应AGV，从H15 到达出入口路径如图5所示，经过路径即为：H15---9---6---3---2---S（1），最短路径为：97.5。

图5 H15到达S的最短路径及长度

采用本算法进行实验可以求出AGV 从H15 到达出入口，再从出入口把待存车到达所有空闲车位的最短路径，如表2 所示。

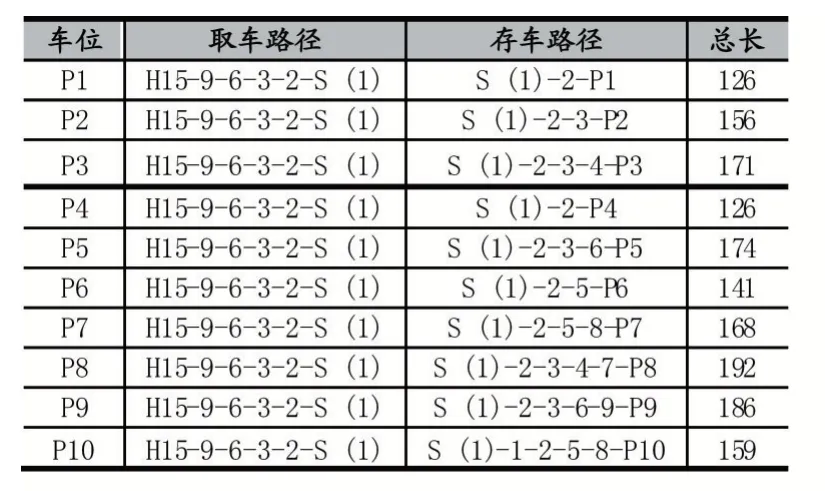
表2 最短路径及总长

通过MATLAB 算法编程可以求解出每个空闲车位相对应的最短的存取车路径及距离总和，验证了算法在智能停车场环境中的可行性和准确性。这样，管理系统在接受到运输任务后，计算器运行编程好的Dijkstra 算法求出空闲车位中的最佳车位，指令AGV 的沿着所规划的路径进行运行，将车运快速准确地送到所指定的位置。实现了运输车辆机器人存取车的高效有序，具有十分重要的意义。

5 结语

根据目前的现状，本文根据智能车库中运输车辆机器人存取车路径所存在的不足进行研究，对其路径规划算法展开研究。基于当前社会智能交通的发展和停车场的实际情况，建立了停车场结构模型，分析了停车场路网，并将路网抽象成带权有向图，将所求最优路径问题转化为了最短路径问题。在对几种最短算法分析比较后，确定了使用Dijkstra 算法进行课题的研究。通过Dijkstra 算法的理论知识和MATLAB 求解，帮助运输车辆机器人找到了最佳车位，求出了各个车位分别对应的最短路径及距离，使得运输车辆机器人的系统得到优化，极大地缩短了AGV 的工作时间，改善了停车场内部的存取车运行效率，节约耗能和成本。