基于仿真的汽车引擎盖强度耐久系统分析

周星栋，王振

（上汽大众汽车有限公司产品研发车身研发部，上海 201805）

通过有限元方法分析某一款车型引擎盖关闭系统的动力学过程，模拟预测引擎盖在整个落锁过程中的应力分布，利用疲劳算法计算疲劳损伤值，提出方案解决局部开裂问题，通过试验验证模型及方案的准确有效，建立一种评价引擎盖疲劳的新方法。

引擎盖；有限元仿真；疲劳计算；应力分析

0 引言

引擎盖是汽车车身结构中最为重要的零件之一，也是新车型设计开发修改最为频繁的零件之一。引擎盖的设计不仅需要考虑到造型的美观，更要兼顾结构刚度、强度、低振动噪声以及行人保护的法规要求，除此之外还要满足工艺可行、轻量化的目标。因此，由于某些轻量化、行人保护能量吸收等结构设计的原因，在引擎盖的疲劳试验中，往往会出现局部应力集中的现象，并且最终导致钣金开裂或者无法锁止的情况发生。

为了解决此类问题，减小因模具修改带来的制造成本和试验成本，在设计之初或者在寻找问题解决方案过程中就需要引入检验钣金应力集中的方法和模式。而通过有效的有限元模型分析模拟引擎盖开启关闭的动力学仿真模型，可以有效地预测风险或者优化开裂解决方案。

本文通过建立引擎盖系统的一整套有限元模型，包括钣金系统、附件缓冲系统、锁系统，利用有限元求解器求解某车型引擎盖关闭落锁过程的瞬态响应，利用应力结果进行疲劳分析，提出改进方案，最终通过试验验证模型和方案的有效，形成了一整套的应力强度和疲劳分析分析解决方法。

1 有限元模型以及分析类型

1.1 引擎盖模型

以某一款车型的引擎盖作为模型输入。引擎盖的钣金通过壳单元建立，钣金之间的胶水连接方式使用实体共节点的方式，焊点使用Abaqus Fastern 方式连接。（图1）胶水问题共节点处理相比多点约束方式可以防止由于胶水弹性模量过小引起的变形过大问题。钣金结构单元全部采用减缩积分单元[1]，保证准确的同时减少计算时间，同时不考虑非线性材料而是在后期结果处理通过Neuber-hyperba[2]等效转换实现。

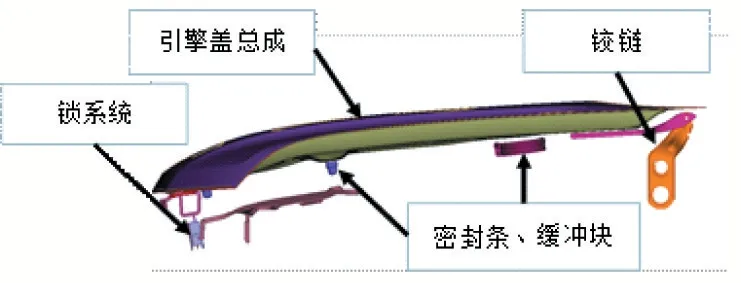
图1 引擎盖有限元模型

1.2 缓冲块、密封条单元以及材料参数

作为缓冲元件的缓冲块以及密封条属于橡胶材料，采用HyperElasticPolynomial 通过能量法Mooney-Rivlin 模型[3]方法拟合。不可压缩橡胶材料的Mooney-Rivilin 模型为[3]：

式（1）中，W 为橡胶材料应变能密度函数，C1与C2为力学性能常数，用来拟合材料拉伸试验等的参数。该模型能很好的描述变形小于150%的橡胶材料力学性能。确定C1和C2的具体方法根据试验测出。不同λ主伸长比下的主应力t1，以为1/λ横坐标纵坐标，以为纵坐标，把试验点绘在坐标系中，并把试验点回归成一直线，C1即为这条直线的截距，C2即为这条直线的斜率。如下图2 所示，Mooney-Rivlin 曲线拟合缓冲块橡胶材料EPDM，基本吻合试验测试数据。

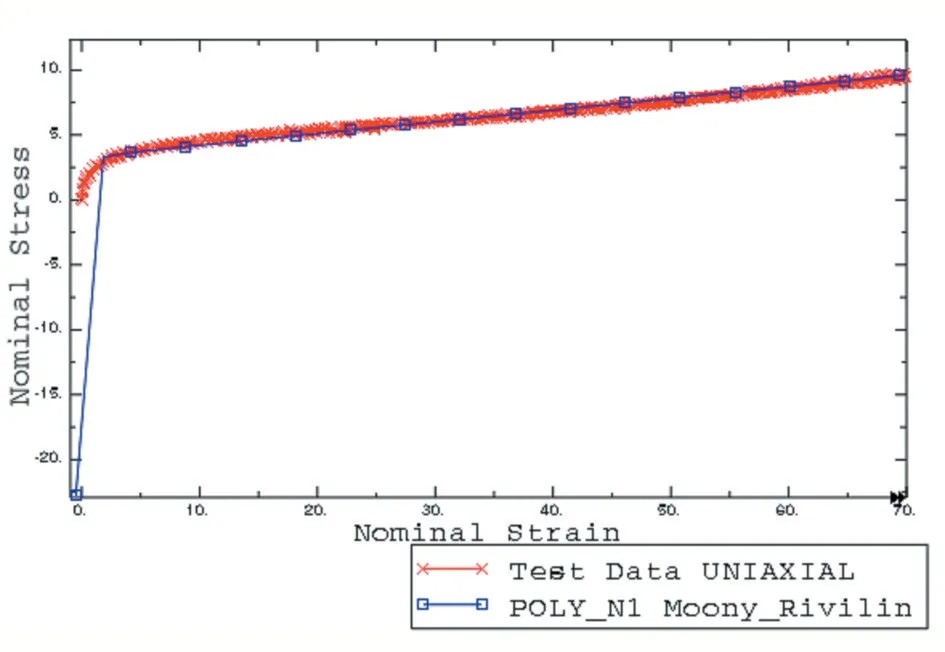
图2 利用Mooney-Rivlin拟合单轴拉伸曲线与试验的对比

密封条的网格截面采用双层网格大小为1-1.5mm，扫掠长度方向大小为3mm。缓冲块网格单元大小为1.5mm，单元格式为减缩积分单元，为防止剪切自锁，网格层数可以增多（图3）。

图3 密封条和缓冲块网格

1.3 锁系统的多体运动学机构

锁系统是引擎盖整个关闭模型的主要组成部分，由于锁内部有许多的零件构成的机构，因此这一部分建模属于多体运动机构建模（图4）。采用CONN3D2单元类型模拟锁内的弹簧，HINGE 类别，对于弹簧刚度使用材料控制，初始预紧力加载。由于锁内部的锁舌等部件在机构运动中需要接触，因此此部分在模型中采用通用接触。

图4 锁模型示意

其中1、2、3、4、5、6 分别为锁系统结构零件Joint_1、2、3、4 为锁内弹簧。

1.4 求解类型选择

对于多接触冲击问题这里使用显示动力学[4]求解类型，即为瞬态显示算法，计算时间设为0.1s。

显示算法使用中心差分迭代[4]方法如下：

显示差分方法的关键位置在确定第一步步长：

式（4）中MNJ为质量矩阵，P 是外部作用力，I 是内部作用力。显示算法不需要总体刚度矩阵计算，允许在某些不影响结果的单元进行质量缩放，以减少计算时间。在此我们并不进行质量缩放，但对极限小的单元进行修正（考虑提高最小单元长度Lmin）。单元与单元的稳定时间步长计算公式：

式（5）中cd为扩散波速率。

从式（5）可以看出稳定时间步长极限，不仅仅与最小单元长度有关。对于线弹性材料：

从式（6）可以看出材料的特性会影响波速，对于非线性材料，随着材料的屈服，刚度会变小，导致波速减小，稳定极限之会随之增大。

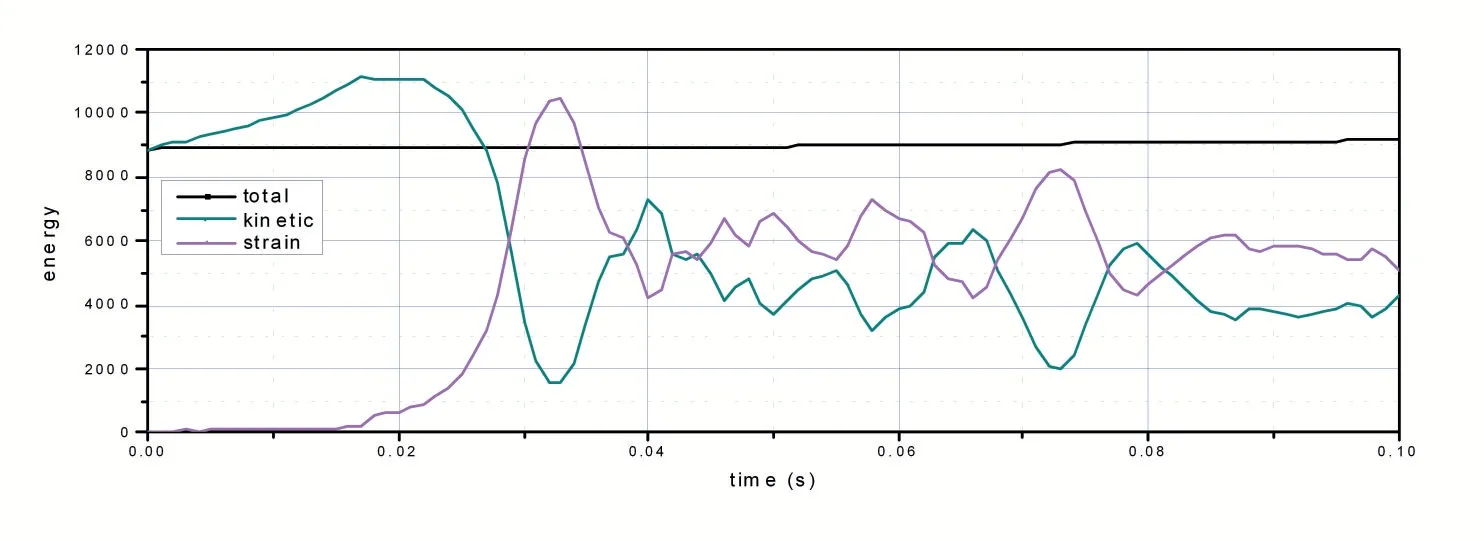
图5 总能量变化曲线

2 结果输出分析

2.1 显示结果合理性分析

显示计算的结果因为是上一步结果的递推结果，一旦超过稳定极限步长就会变得与实际变形方式不一致，也就是失真。因此需要比较计算过程中总体能量的变化，控制在变化率不超过5%，另外应变能与内能的比值小于10%。图5 为模型内能总能量以及应变能。计算结果总能量变化在2%以内，可以认为模型结果准确。

2.2 引擎盖内板应力分布

引擎盖关闭试验开裂部分情况如下（3750 次循环之后）在内板表面发现裂纹。引擎盖作为内外钣金的总成零件，关闭落锁过程中，主要受到锁和缓冲系统的冲击力，其中锁占了绝大部分。从图6 看出，裂纹发生在引擎盖锁扣安装面圆角位置。

图6 试验结果开裂区域

对比模拟结果应力分布如图7。可以看出应力集中的位置即是引擎盖锁扣安装面圆角过度位置，初步的原因分析是此处局部结构过度太急，刚度不够，导致应力集中。

3 疲劳分析

瞬态动力学模拟的结果，包含了在关闭时间内的应力变化历程，对于这些时刻的应力，把它作为疲劳分析的应力输入。这里采用Miner Elementary[6]方法修正S-N 曲线，同时利用雨流技术[7]对瞬态应力进行统计学计数如图8 所示。

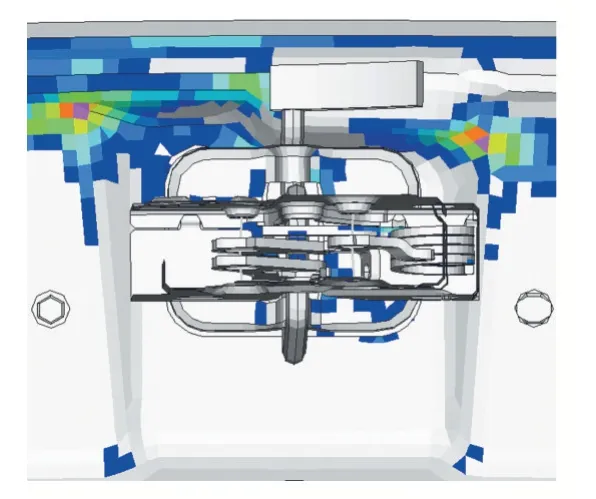
图7 应力分布

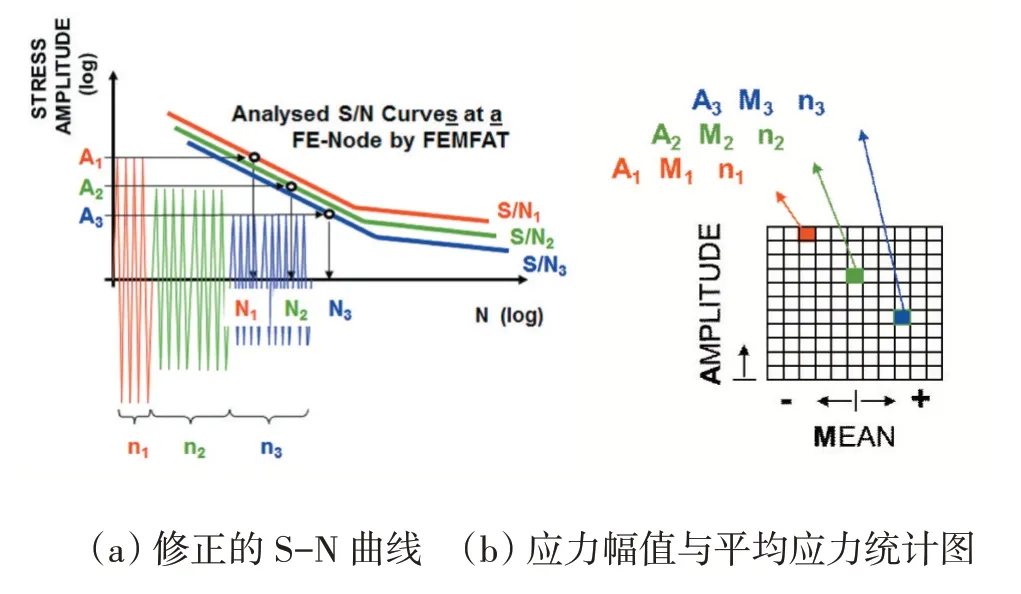
图8 雨流技术

A：节点应力瞬态幅值M：平均应力n：雨流技术幅值统计数量

雨流技术采用Unfavorable Sequence[8]处理，即考虑应力叠加最苛刻的顺序，这样疲劳分析模拟结果更为保险。

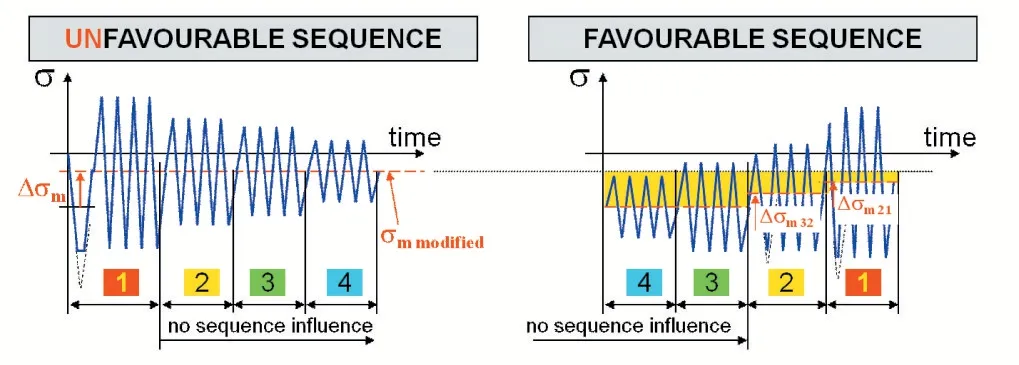
图9 应力序列方法

对于弹性材料利用Neuber-Hyperbola 方法通过应变能[9]等效方法影射到塑形材料。Neuber-Hyperbola方法原理就是在知晓材料塑性材料的基础上，将不考虑塑性的弹性体应变能等效为同等非线性材料的应变能，这样将非线性放在了计算求解之后，作为应力整理过程的处理，可以大大的减少计算时间，避免由于引入非线性材料导致的问题。

图10 Neuber-Hyperbola方法

4 方案及模拟结果分析对比

锁加强版在右侧圆角位置没有与钣金的钣金加强面，并且此处的内板圆角过小，在落锁的过程中导致此处的变形过大，进而导致应力集中（图11）。显而易见，需要在这个位置对内板进行加强，将锁加强板延出，并与内板通过胶水连接，同时放大内板此处的圆角避免局部造型变化剧烈导致的应力集中。优化的方案如图12 所示，对于开裂的位置进行加强版的补强，同时对于圆角进行适当的扩大，在考虑到无法进行焊点连接，设计为胶水连接方式。

图11 结构及变形分析

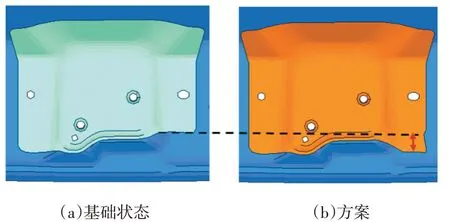
图12 方案措施

方案和基础模型的应力分布对比，方案状态明显应力等级降了一个水平，修补的锁加强板起到了加强刚度的作用（图13）。

图13 应力对比

在此基础上，将应力结果输入到疲劳分析瞬态结果计算中可以得到疲劳分析结果，5000 次循环后的损伤系数为如图14 所示，基础状态下损伤系数[10]为2.1远大于1，存在开裂风险，这也与试验结果一致，而优化方案此处损伤系数为0.1，应该能保证避免此处避免开裂的风险，接下来，需要通过试验验证结果。

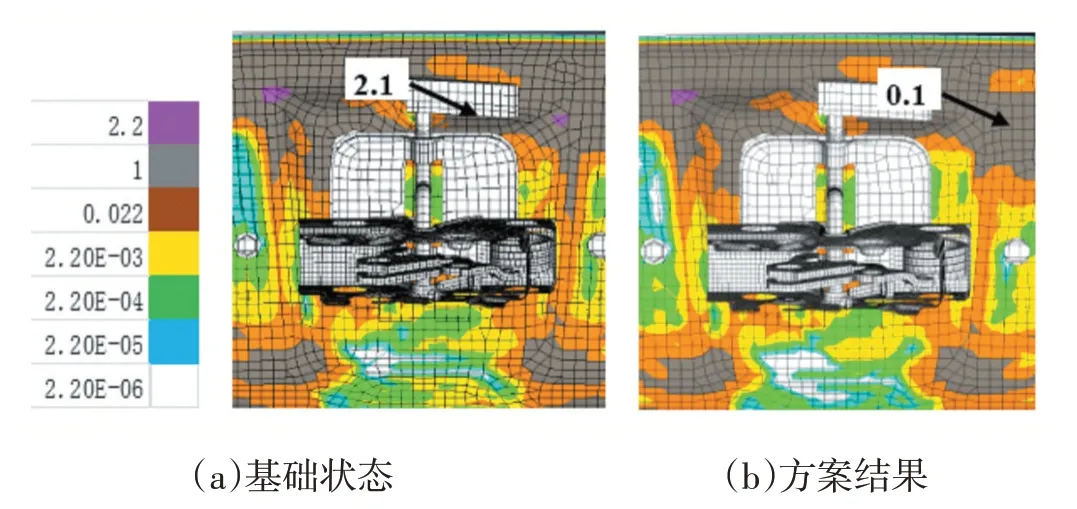
图14 疲劳损伤值对比

5 试验验证

方案措施在5000 次引擎盖关闭试验中的结果图15，试验检测没有出现裂纹，因此方案是有效的，整个制造试验流程也得到了可行性确认。

图15 方案试验结果

6 结语

汽车引擎盖在开启与关闭落锁的过程中需要承担相应的强度、疲劳要求，并结合工艺要求保障结构的优化设计以减少不必要的开发费用，因此需要一种结合分析与试验的方法评价设计结构。

本文通过分析某车型在预生产阶段出现的开裂问题，充分利用模拟计算方法分析引擎盖的结构缺陷，在生产工艺允许的范围内快速找出改进措施，并通过计算手段验证了方案应力水平以及疲劳极限上的可行性，在短时间通过试验验证了解决方案，形成了一整套的试验-计算检验方法。此分析方法及其建模方式可以作为新车型的引擎盖强度疲劳风险的标准化评估手段。