优先队列分支限界法解多货车多货箱装载问题

2019-06-01付志英吕梦鸽王谷青贺晴王蒙武杰

现代计算机 2019年12期

付志英，吕梦鸽，王谷青，贺晴，王蒙，武杰

（陕西师范大学计算机科学学院，西安 710119）

由于车辆配备有限而快件量爆炸增长，使得物流企业快件派送的服务质量和派送时效无法有效满足需求。为了解决该问题，提出一种基于优先队列分支限界思想的算法并应用于多货车多货箱装载问题的求解。该方法利用贪心策略，采用分阶段分支限界方法装载每辆货车。实例分析表明应用该算法可以获得多货车多货箱问题的可行方案。

优先队列分支限界法；贪心策略；分阶段决策；装载问题

0 引言

2018年，“双11”落下帷幕，各方面数据再次刷新纪录，当日物流订单量突破10 亿大关。因此，在车辆配备有限而快件量爆炸增长的情况下，合理有效地对快件进行装载是应对当前物流需求，提高配送效率的核心问题。

本文针对多辆货车、多个货箱的装载问题，首先对该问题进行了分析。当使用两辆货车进行装载时，货车的装载次序与装载可行性无关；当货车数量大于2时，货车的装载次序与装载可行性具有很大相关性。其次，针对这一问题，本文采用贪心策略和优先队列分支限界法分阶段对多货车多货箱装载问题进行建模求解。最后，实验表明，本文所提算法可以有效搜索到多辆货车多个货箱装载问题的可行解。

1 装载问题

1.1 多货车多货箱装载问题定义

设现有m辆货车来装载n个货箱（货箱不可拆），第i辆货车的最大载重量为Ci(i=1,2,…,m)，第j个货箱的重量是Wj(j=1,2,…,n)。现在需要求解一种装载方案使得全部货箱均装入货车。易证明，若给定的装载问题有，可通过下面的方案得到可行解：

（1）首先将第一辆货车尽可能装满；

（2）然后从剩余车辆中选择一辆车，并尽可能将其装满；

（3）重复步骤（2）直到所有货箱均装下。

当只有两辆货车时，其装载序列最多有两种，且通过数学证明可以发现货车的装载次序与装载可行性无关。即若采用一种货车的装载序列可以装下，则另一种装载序列也可以装下。证明如下：

（设两辆货车分别为A、B，其对应最大载重量为WA、WB）

装载序列一：先装A 后装B 有可行方案，即：

货车A 的实际装载量：

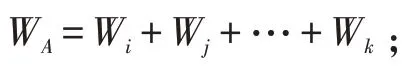
货车B 的实际装载量：

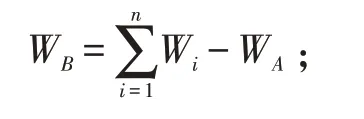
装载序列二：按照先装B 后装A 的顺序装车，货车B 的实际装载量，即：

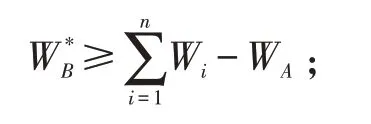
待装车的货箱总重量：

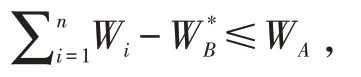
此时，货车A 一定能装下剩余货箱。

综上所述，当货车数为2 时，货车的装载次序与装载可行性无关。然而，对多于两辆货车的装载问题，其装载序列有多种，且货车的装载次序与装载可行性有关。即若采用一种货车的装载序列不能装下货箱，但是可能存在另一种装载序列可以装下货箱。在此基础上，我们提出了两种假设，即：①按照货车载重量从大到小的顺序装载，若不能完全装载货箱，则按其他的货车顺序装载货箱都不能装下；②按照货车载重量从小到大的顺序装载，若不能完全装载货箱，则按其他的货车顺序装载货箱都不能装下。经过实例验证（如表1-4），我们发现存在不符合这两个假设的情况。故，对于多货车多货箱装载问题（货车数＞2），货车装载序列与装载可行性有关。

表1 假设1 货车与货箱的信息

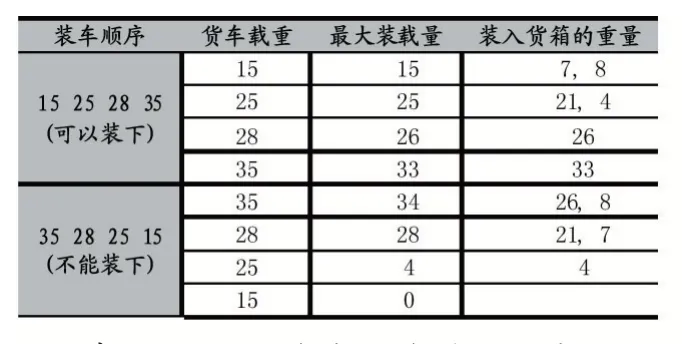
表2 假设1 货车的两种装载方案与可行性验证

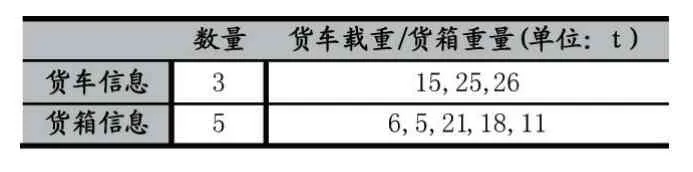
表3 假设2 货车与货箱的信息

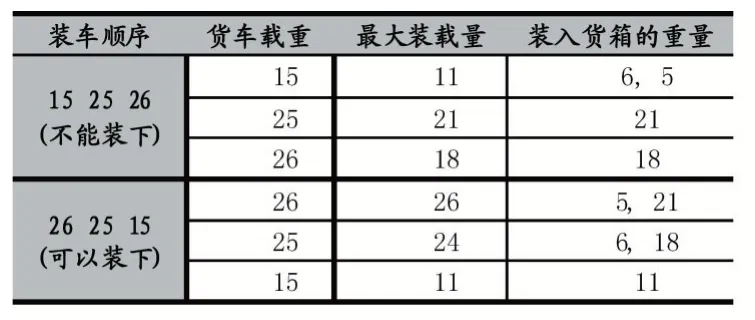
表4 假设2 货车的两种装载方案与可行性验证

1.2 装载问题数学模型

根据1.1 小节所述，解决问题的关键是在一种特定的货车装载序列下，装载每一辆货车时装尽可能多的货箱。因此，装载每一辆货车的过程可以看作一系列的决策过程，即在装载每一辆货车时决策哪些货箱要装车，哪些货箱不装。由此，求解多货车多货箱装载问题，就是在一种货车装载顺序下，对于m辆货车n个货箱且找出一个m元向量，其中1 ≤k≤n,1 ≤i≤m（k,i为整数，1 表示装载该货箱，0 表示不装载该货箱）。多货车多货箱可表示为如下0-1 整数规划数学模型：

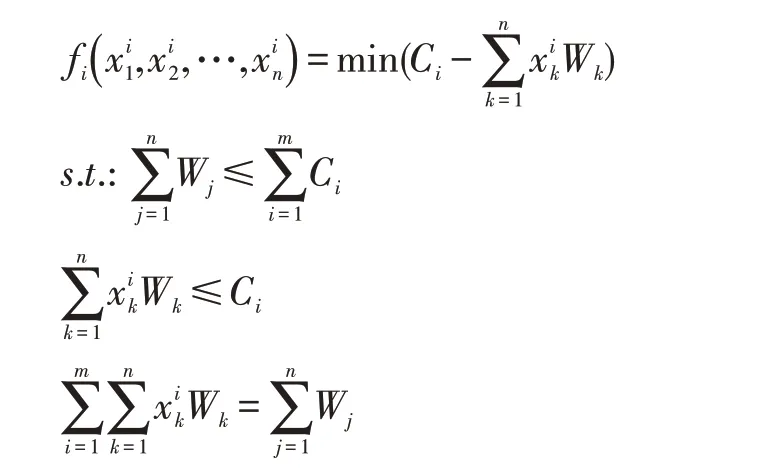
其中,fi为第i辆货车的装载货箱空闲空间最小的目标函数，即尽可能装满每一辆货车。

2 利用优先队列分支限界法解决多辆车多货箱装载问题

2.1 装载问题数学模型

优先队列分支限界法属于一种常用的树型搜索算法，其中限界是在分支搜索的基础上加入结点限制，对以不满足条件的结点为根的分支子树不再进行搜索，以此缩小搜索范围，提高搜索效率；优先队列是对活结点表进行优先队列组织，每次扩展结点都从当前活结点表中选择一个优先级最高（最有利）的结点，使每一步搜索向最优解靠近。当扩展到叶结点时，就得到一个最优解。优先队列使用数据结构“堆（heap）”实现，每次都取优先级最高的元素即堆顶元素作为下一个扩展节点。如图1 为装载一辆货车时，使用优先队列分支限界法进行分析。

2.2 装载问题数学模型

由1.1 小节装载问题定义可知，多货车多货箱装载问题属于多辆货车的装载组合最优化问题。由于货车数量、每辆货车的载重量和货箱数量、每个货箱的重量都不确定，导致整体可行装载方案不易求出。故，当有m辆货车时，对给定的一种货车装载序列分为m个阶段依次进行装载，尽可能将每一辆货车装满，且在装载每一辆货车时，采用优先队列分支限界法搜索货箱装载的解空间树。当货车的载重量不同时，多辆货车存在多种装载序列，且多辆货车装载方案可行性与货车装载序列有关，因此，该问题就转化为遍历所有货车装载序列，搜索可行解的问题。本文为了提高搜索的效率，选择采用具有树型搜索结构的优先队列分支限界法来解决多货车多货箱装载问题，并要求找到一个可行解即停止搜索。

采用优先队列分支限界法解决多货车多货箱装载问题中的限界条件为：结点装载上界大于当前最优方案，并且从该结点到根结点路径对应的装载方案，其装载量不超过当前装载货车的载重量，且结点的装载上界等于当前装载货车已装载货箱重量加上即将被装载物品的重量；当前最优方案是指从初始到当前所有状态中，能够装载货箱的最大总重量。

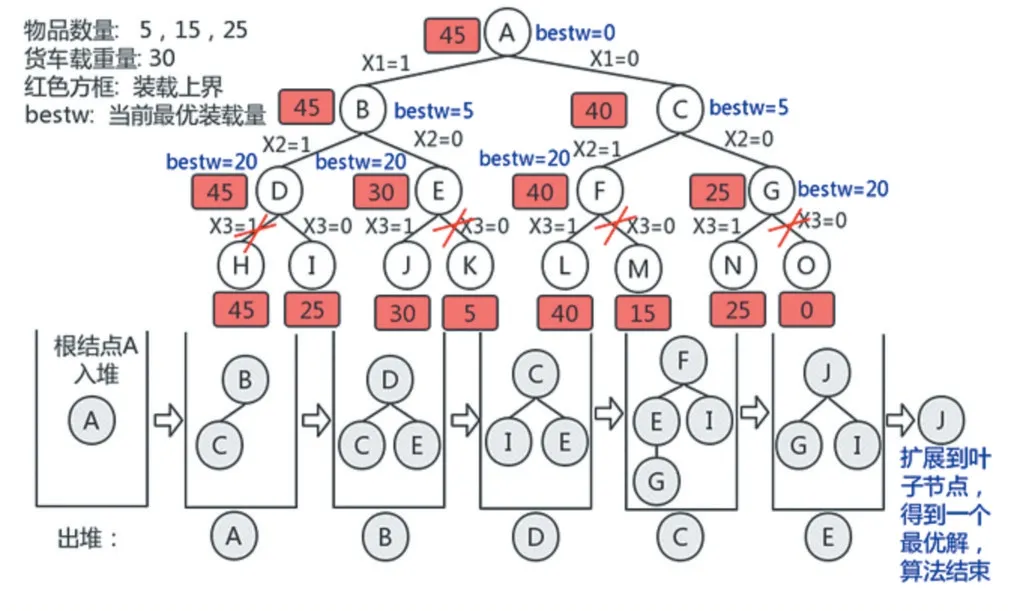
图1 装载一辆货车的解空间树

2.3 算法流程图

总体上来看，本算法的流程主要由两层循环嵌套实现，第一层循环调用一个全排列函数（next_permutation）对所有货车装载序列进行遍历；第二层循环调用自己实现的一个最大装载函数（MaxLoading）对第一层循环给定的装载序列分为m个阶段依次进行装载。执行第一层循环时，为了降低时间复杂度，当找到一种可行装载方案时就退出循环；执行第二层循环时要搜索到解空间树叶子结点时才退出循环。

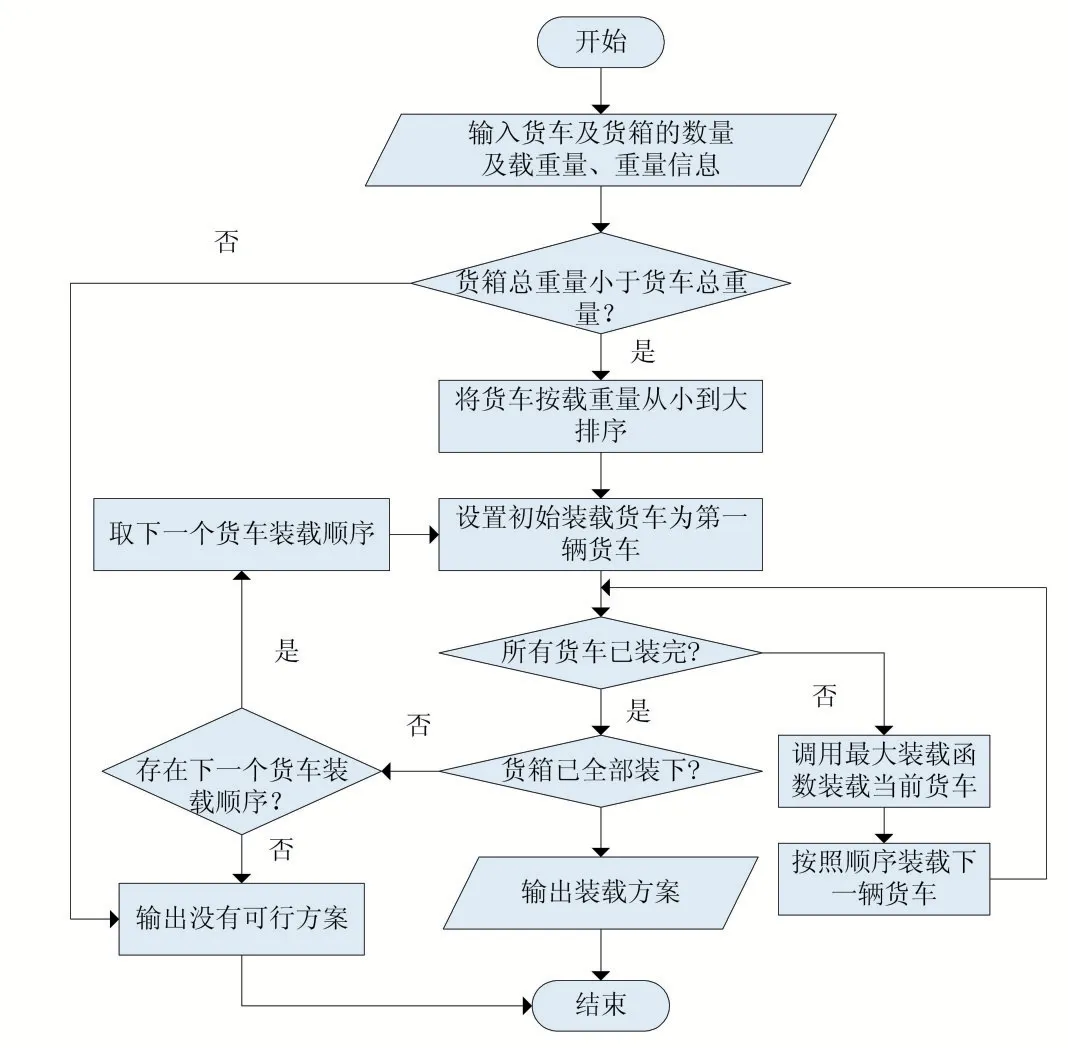
图2 优先队列分支限界解决多辆货车多货箱装载问题流程图

2.4 算法实现

为了实现问题求解，本文采用C++面向对象程序语言来进行计算机求解。其中，本文所定义的关键类如下：

（1）堆结点关系类，用于记录活结点的装载上界，父亲结点等信息：

（2）堆结点类，用来创建堆结点：

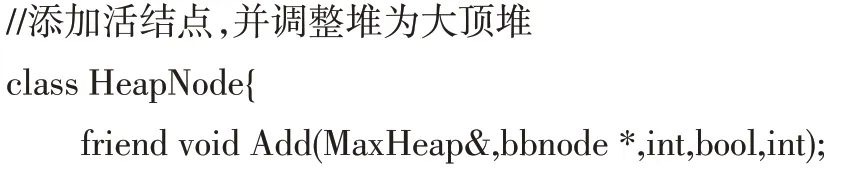
（3）大堆类，用来创建一个大堆对象，在对大堆进行插入或删除堆结点时，调整堆型以形成最大顶堆：

2.5 算法时间复杂度

本文在采取遍历货车装载序列的同时，采用找到一种符合条件的装载顺序就退出循环的方法来降低时间复杂度，当遍历到最后一个货车次序才找到可行解时，算法的时间复杂度最大，值是O(log(m!*m*n))。其中m为货车数量，n为货箱数量，m!为遍历货车的所有装载顺序。当按照第一个货车次序进行装载就能找到可行解时，算法的时间复杂度最小，值为O(log(m*n))。