数字通信系统中Eb/N0与SNR转换方法的研究

张少侃，吕聪敏，甘浩

（广州海格通信集团股份有限公司，广州 510663）

基于实际数字通信系统中Eb/N0 与SNR 转换的需求，从Eb/N0 和SNR 的基本概念、定义出发，通过严密的公式推导，给出Eb/N0 与SNR 之间的一般性转换公式。并针对实际系统中白噪声的不同测量带宽，给出不同的Eb/N0 与SNR 转换公式。给出MATLAB 系统仿真中Eb/N0 与SNR 的具体转换公式，最后通过实际通信系统的案例分析，给出实际系统的Eb/N0 与SNR 转换公式参数应用。

Eb/N0；SNR；MATLAB；数字通信系统

0 引言

现代数字通信系统中，接收机端所能接收的最小SNR 和Eb/N0[1-3]是衡量通信系统的重要指标。SNR 也即信噪比，是接收端模拟信号的重要测量指标，可以通过频谱仪等仪器实际测量接收端的模拟信号得到。而Eb/N0 是指通信系统传输一比特信息所需要的能量和噪声功率谱密度的比值，是衡量整个通信系统性能归一化的一个系统指标。由于在数字系统传输中会采用不同的调制技术，而不同进制的调制技术下频谱效率会不同[4-5]，一个由k 个比特映射生成的调制符号所实现的频谱效率就为k bit/s/Hz。这种情况下，在计算比特误码率的时候考虑的是通信系统的整体性能，如果要横向比较系统的整体性能，就要将系统效率的作用排除在外，此时就必须从单个比特着手去比较，而Eb/N0 恰好可以排除频谱效率引起的问题。一般情况下，模拟通信系统常采用SNR～BER 来衡量通信系统的性能，数字通信系统常采用Eb/N0～BER 来衡量通信系统的性能。由于数字通信系统[6]常采用Eb/N0 作为衡量系统的性能指标，但实际测量Eb/N0 比较困难，故而研究Eb/N0 与SNR 的转化关系变的十分重要。

本文从两种指标的基本概念出发，通过基本概念定义和公式转化详细地推导出两者之间的转化关系，并在转换公式的基础上阐述了实际测量中不同的SNR测量方法导致的不同SNR 与Eb/N0 转换公式以及MATLAB 系统仿真中SNR 与Eb/N0 的转换公式。最后，通过实际的通信系统案例给出SNR 与Eb/N0 的转换关系。

1 符号定义与说明

在进行公式推导之前首先给出本文中后面出现的主要符号的定义。下面给出本文中用到的符号及其定义说明。

Eb：单位比特的能量，单位是焦耳（Joules）；

N0：噪声的功率谱密度，单位是瓦特/赫兹（Watts/Hz）；

Joules·Hz/Watts=Joules·（1/1s）/（Joules/s）=1

S：信号功率，单位是瓦特（Watts）；

N：噪声功率，单位是瓦特（Watts）；

br：用户信息的传输速率，单位是比特每秒（bit/s）；

Tb：传输每比特信息所需要的时间，单位是秒（s），Tb=1/br；

sr：信道中的符号传输速率，单位是符号每秒（symbol/s）；

Rc：通信系统的信道编码速率；

Rm：通信系统的调制率，Rm=log2（M），M 是调制星座点个数，如BPSK，M=2，QPSK，M=4，256-QAM，M=256；

d：扩频倍数；

insValue：平方根升余弦滚降成型滤波器的插值倍数；

α：平方根升余弦滚降滤波器的滚降因子；

W：传输信道带宽。

2 转换公式推导

本节对Eb/N0 与SNR 转换公式做推导，根据定义我们有：

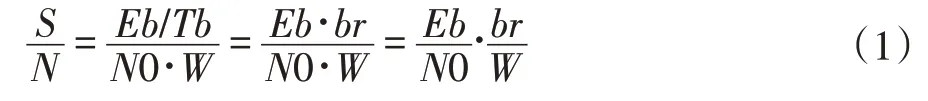
上式中，根据定义，信号的功率S 等于传输每比特信息所需的能量Eb 除以传输每比特所需要的时间Tb。噪声的功率N 等于噪声功率谱密度N0 乘以传输信号的信道带宽W。又根据调制速率和编码速率的定义我们有：

将式（2）和式（3）代入式（1）得到：

对（4）式两端同时取10∙log10()便可得到转换公式的对数形式：

对于CDMA 体制通信系统，假设系统用户个数为U 个，U 个用户数据之间通过正交码字直序扩频叠加起来一起传输，假设ST为U 个用户数据叠加的信号总功率，S 为单个用户数据的信号功率，则有ST=U∙S，而我们在接收端测量模拟信号的功率只能测量叠加的所用用户信号总功率ST，因而，对于CDMA 体制通信系统，Eb/N0 与SNR 的转换公式为：

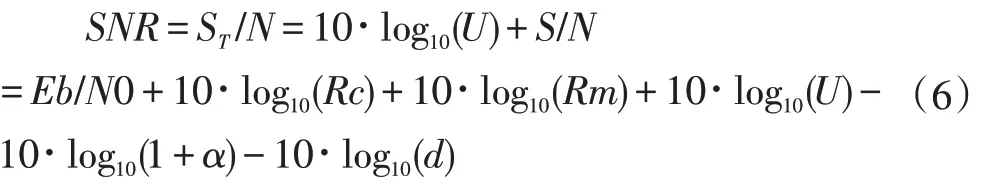
式（6）为通用转换公式，对于FDMA 和TDMA 体制通信系统，令U=1 即可。

上述的Eb/N0 与SNR 转换公式没有考虑系统帧结构中用于同步的导频序列开销，一般的通信系统导频序列所占的开销小于10%，因而一般通信系统的帧结构效率在90%之上，由于10∙log10(0.9)接近于0，因而一般的转换公式可以省略不做考虑，对于精度要求比较高的系统，在公式转换时应考虑帧结构效率的影响。

3 不同的SNR测量方法对应的不同转换公式

对于一般的通信系统，发端成型滤波器和收端匹配滤波器是一致的，常见的均为平方根升余弦滚降滤波器。假设成型滤波器和匹配滤波器均采用平方根升余弦滚降滤波器，则其频谱如图1 所示。

图1 平方根升余弦滚降滤波器频谱示意图

平方根升余弦滚降滤波器的频率响应表达式为：

其中fN=sr/2=1/2Ts，为信道符号速率的一半。

一般情况下，我们在实际测试时，我们要测量信号的完整功率必须测量的信号带宽是W，而不能是sr，只有测量W 带宽内的信号才能不漏掉信号功率，因为发端信号的频谱就是图1 中的平方根升余弦滚降成型滤波器波形（发端成型滤波的波形）。而在测量噪声功率时，这时候我们可以测量sr 带宽，也可以测量W 带宽。由公式（7）可以知道，图1 中的1、2、3、4 阴影部分的面积全部是相等的。根据1、2、3、4 阴影部分面积全部相等，我们可知测量sr 带宽的白噪声功率也就是等于白噪声通过匹配滤波后的功率（白噪声频谱是平坦的，通过匹配滤波后的白噪声形状就是上图中的平方根升余弦滚降滤波器频谱）。这也就是说测量sr 带宽的噪声功率就是测量白噪声通过匹配滤波器后的功率，测量W 带宽的噪声功率就是测量白噪声通过匹配滤波器之前的功率。这里把两种测量的噪声功率分别记为Ns（sr 带宽的噪声功率）和Nw（W 带宽的噪声功率）。我们可知Nw=（1+α）∙Ns，这样就有：

根据上述原理，我们得到，当实际测量的噪声功率带宽为sr 时（测量信号功率的带宽必须为W），Eb/N0与SNR 的转换公式为：

当实际测量的噪声功率带宽为W 时（测量信号功率的带宽必须为W），Eb/N0 与SNR 的转换公式为：

所以，实际采用的噪声功率测量带宽决定了EbN0和SNR 的具体转化公式，而不管怎么测试噪声功率，信号的功率测量必带宽须为W。

4 MATLAB仿真中的Eb/N0与SNR转换公式

使用MATLAB 进行通信系统仿真是现代数字通信系统设计中一个非常重要的步骤。通常MATLAB中也是使用信噪比SNR 来添加噪声，不能使用Eb/N0参数进行噪声的添加，但我们通常需要使用Eb/N0 这个归一化指标参数对系统进行评价，因而在MATLAB仿真中也常常需要用到Eb/N0 与SNR 的转换公式。

MATLAB 仿真中添加加性高斯白噪声常常使用函数库中的AWGN 函数进行添加，然而使用AWGN 函数添加的加性高斯白噪声是按照上节中所述的sr 带宽进行添加的，也即添加的噪声功率是按照通过匹配滤波器后的噪声功率计算的。这样在MATLAB 进行整个通信系统仿真时，计算Eb/N0 与SNR 转换公式时应该按照式（9）进行转换，不需要计算平方根升余弦滚降因子α的影响。

然而，MATLAB 仿真中的转换公式不是完全按照公式（9）进行转换的。由于在MATLAB 仿真中发端信号在添加完噪声以后，在收端要进行匹配滤波处理，数字信号进过匹配滤波后功率会增大insValue 倍，而添加的噪声在经过匹配滤波后功率无变化，而我们对解调解码的信噪比衡量是以匹配滤波后的参数为基准的，包括上面模拟域测试的SNR 也是计算的是匹配滤波后的信噪比，因而MATLAB 仿真中Eb/N0 与SNR 的转换公式为：

5 实例分析

假如某CDMA 体制通信系统，每个用户的数据传送速率为1kb/s，信道编码采用编码速率为Rc=1/3 的卷积编码，星座映射采用QPSK 调制方式，基带脉冲成型采用因子为α等于0.35 的平方根升余弦滚降函数，上采样倍数insValue 为8，直序扩频倍数d=16，系统中的用户个数U=3。

首先来看一下各路用户数据经过各模块后数据速率的变化，原始信息速率为1kb/s，1/3 卷积编码后变为3kb/s，也就是每秒传送3000bit 数据，采用QPSK 调制后，速率变为1.5k symbol/s，经过直序扩频后，符号速率变为24k symbol/s。

（1）模拟域噪声测量带宽为W

当在模拟域测量的白噪声带宽为W 时，我们使用的Eb/N0 与SNR 转换公式为式（10），因此其具体的转换公式为：

使用dB 表示，转换公式为：

（2）模拟域噪声测量带宽为sr

当在模拟域测量的白噪声带宽为sr 时，我们使用的Eb/N0 与SNR 转换公式为式（9），因此其具体的转换公式为：

使用dB 表示，转换公式为：

（3）MATLAB 系统仿真中的转换公式

在使用MATLAB 工具进行系统仿真时，我们使用的Eb/N0 与SNR 转换公式为式（11），因此其具体的转换公式为：

使用dB 表示，转换公式为：

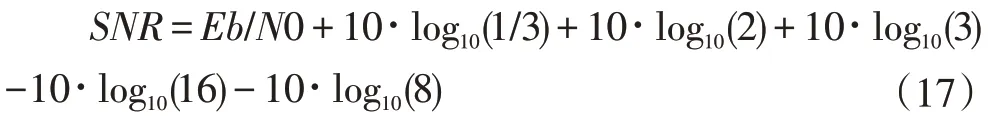
6 结语

针对通信系统中Eb/N0 与SNR 的转换问题，本文从基本概念出发，通过理论公式推导，得到了Eb/N0 与SNR 的一般转换公式。继而针对模拟域测量的不同白噪声带宽，详细地推导出了不同的Eb/N0 和SNR 转换公式。而后针对MATLAB 系统仿真场景，详细说明了MATLAB 仿真中Eb/N0 和SNR 具体转换公式。最后本文给出了一个实际通信系统案例分析，具体地列出了Eb/N0 与SNR 转换公式。